Rating Iron Deficiency in Soybean Using Image Processing and Decision-Tree Based Models
Abstract
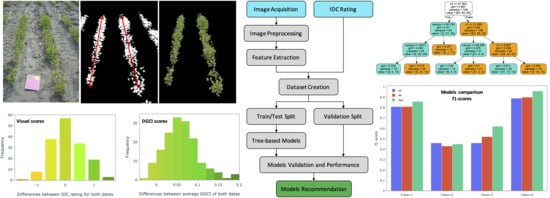
:1. Introduction
2. Materials and Methods
2.1. Field Experimental Plots
2.2. Overall Methodology
2.3. IDC Visual Rating
2.4. Image Acquisition
 ) board. The standard HSB values of yellow disk are 50, 87, and 91 (#e7c71f hex; 231, 199, 31 RGB;
) board. The standard HSB values of yellow disk are 50, 87, and 91 (#e7c71f hex; 231, 199, 31 RGB;  ) and for green disk are 91, 38, and 42 (#576c43 hex; 87, 108, 67 RGB;
) and for green disk are 91, 38, and 42 (#576c43 hex; 87, 108, 67 RGB;  ), which produced the DGCI (Equation (1)) values of 0.0178 for yellow and 0.5722 for green disk [17]. These known DGCI values of disks were used along with the observed values of these disks from the image to calibrate DGCI values of soybeans.
), which produced the DGCI (Equation (1)) values of 0.0178 for yellow and 0.5722 for green disk [17]. These known DGCI values of disks were used along with the observed values of these disks from the image to calibrate DGCI values of soybeans.2.5. Object Recognition in Field Image
2.5.1. Extraction of Standard Color Board
2.5.2. Extraction of the Yellow and Green Disks from the Color Board
2.5.3. Detecting Plot Middle Rows
2.5.4. Color Vegetation Index
2.6. Machine Learning Models
2.6.1. Decision Tree Classifier
2.6.2. Random Forest Classifier
2.6.3. Adaptive Boosting (AdaBoost) Classifier
2.6.4. Models’ Input Features
2.7. Imbalance Dataset Oversampling Technique
2.8. Performance Assessment of Machine Learning Models
3. Results
3.1. Results of Distribution of the Image Input Features, Visual Scores, and Merged Rating of IDC Progression
| Data | 3 July 2014 (Date 1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| (n = 160 Each) | Normalized | IDC | DGCI* | SD | DGCI Ranges | ||||
| Canopy Size | Score | DGCI | |||||||
| Average | 31.34 | 1.98 | 0.23 | 0.11 | 41.52 | 50.07 | 8.15 | 0.26 | 0.0 |
| SD | 8.98 | 0.54 | 0.04 | 0.01 | 15.28 | 11.97 | 3.86 | 0.23 | 0.0 |
| Minimum | 14.23 | 1.00 | 0.14 | 0.09 | 8.03 | 21.24 | 1.92 | 0.01 | 0.0 |
| First Quartile | 24.80 | 1.50 | 0.20 | 0.10 | 30.86 | 40.17 | 5.35 | 0.12 | 0.0 |
| Median | 30.93 | 2.00 | 0.23 | 0.11 | 41.56 | 50.98 | 7.43 | 0.20 | 0.0 |
| Third Quartile | 35.47 | 2.50 | 0.26 | 0.11 | 53.58 | 59.18 | 9.92 | 0.33 | 0.0 |
| Max | 56.58 | 3.00 | 0.33 | 0.13 | 76.81 | 73.92 | 23.92 | 1.29 | 0.0 |
| 17 July 2014 (Date 2) | |||||||||
| Average | 52.12 | 2.06 | 0.29 | 0.11 | 20.93 | 62.64 | 15.08 | 1.28 | 0.07 |
| SD | 14.99 | 0.85 | 0.03 | 0.02 | 9.00 | 7.97 | 7.16 | 1.91 | 0.27 |
| Minimum | 9.26 | 1.00 | 0.22 | 0.07 | 4.21 | 41.31 | 3.63 | 0.01 | 0.00 |
| First Quartile | 41.65 | 1.00 | 0.27 | 0.09 | 14.38 | 56.91 | 9.79 | 0.26 | 0.00 |
| Median | 52.10 | 2.00 | 0.29 | 0.10 | 19.96 | 63.36 | 13.98 | 0.60 | 0.00 |
| Third Quartile | 61.63 | 3.00 | 0.31 | 0.12 | 27.07 | 69.23 | 19.49 | 1.22 | 0.00 |
| Max | 100.00 | 4.00 | 0.41 | 0.18 | 44.56 | 79.06 | 39.01 | 10.06 | 2.03 |
3.2. Performance Assessment Results of Machine Learning Models
3.2.1. Decision Tree
3.2.2. Random Forest
3.2.3. AdaBoost
3.3. Models Input Features and Their Importance
4. Discussion
4.1. Distribution Characteristics of the Image Input Features
4.2. Visual Scores, DGCI Scores, and Merged Rating of IDC Progression
4.3. Performance of Machine Learning Models
4.4. Models Input Features and Their Importance
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A.
Appendix A.1. Removing Soil Background for Plant Rows Extraction

Appendix A.2. Gini and Entropy of the Decision Tree Classifier
Appendix A.3. Normalized Canopy Size
Appendix A.4. Performance of Machine Learning Models
Appendix A.5. Data and Source Codes
References
- ASA. 2019 SOYSTATS A Reference Guide to Soybean Facts and Figures. American Soybean Association. 2019. Available online: https://soygrowers.com (accessed on 17 December 2020).
- Vasconcelos, M.W.; Grusak, M.A. Morpho-physiological parameters affecting iron deficiency chlorosis in soybean (Glycine max L.). Plant Soil 2014, 374, 161–172. [Google Scholar] [CrossRef] [Green Version]
- Naeve, S.L. Iron deficiency chlorosis in soybean. Agron. J. 2006, 98, 1575–1581. [Google Scholar] [CrossRef]
- Bloom, P.R.; Rehm, G.W.; Lamb, J.A.; Scobbie, A.J. Soil nitrate is a causative factor in iron deficiency chlorosis in soybeans. Soil Sci. Soc. Am. J. 2011, 75, 2233–2241. [Google Scholar] [CrossRef]
- Lucena, J.J. Fe chelates for remediation of Fe chlorosis in strategy I plants. J. Plant Nutr. 2003, 26, 1969–1984. [Google Scholar] [CrossRef]
- Nadal, P.; García-Delgado, C.; Hernández, D.; López-Rayo, S.; Lucena, J.J. Evaluation of Fe-N, N′-Bis (2-hydroxybenzyl) ethylenediamine-N, N′-diacetate (HBED/Fe3+) as Fe carrier for soybean (Glycine max) plants grown in calcareous soil. Plant Soil 2012, 360, 349–362. [Google Scholar] [CrossRef]
- Goos, R.J.; Johnson, B.E. A comparison of three methods for reducing iron-deficiency chlorosis in soybean. Agron. J. 2000, 92, 1135–1139. [Google Scholar] [CrossRef]
- Hansen, N.; Schmitt, M.A.; Anderson, J.; Strock, J. Iron deficiency of soybean in the upper Midwest and associated soil properties. Agron. J. 2003, 95, 1595–1601. [Google Scholar] [CrossRef]
- Naeve, S.L.; Rehm, G.W. Genotype× environment interactions within iron deficiency chlorosis-tolerant soybean genotypes. Agron. J. 2006, 98, 808–814. [Google Scholar] [CrossRef] [Green Version]
- Kaiser, D.; Lamb, J.; Bloom, P.; Hernandez, J. Comparison of field management strategies for preventing iron deficiency chlorosis in soybean. Agron. J. 2014, 106, 1963–1974. [Google Scholar] [CrossRef] [Green Version]
- Helms, T.; Scott, R.; Schapaugh, W.; Goos, R.; Franzen, D.; Schlegel, A. Soybean iron-deficiency chlorosis tolerance and yield decrease on calcareous soils. Agron. J. 2010, 102, 492–498. [Google Scholar] [CrossRef] [Green Version]
- Horst, G.; Engelke, M.; Meyers, W. Assessment of Visual Evaluation Techniques 1. Agron. J. 1984, 76, 619–622. [Google Scholar] [CrossRef]
- Van Den Broek, E.L.; Vuurpijl, L.G.; Kisters, P.; Von Schmid, J.C.M. Content-based image retrieval: Color-selection exploited. In Proceedings of the Third Dutch-Belgian Information Retrieval Workshop, DIR 2002, Leuven, Belgium, 6 December 2002; Volume 3, pp. 37–46. [Google Scholar]
- Karcher, D.E.; Richardson, M.D. Quantifying turfgrass color using digital image analysis. Crop. Sci. 2003, 43, 943–951. [Google Scholar] [CrossRef]
- Vollmann, J.; Walter, H.; Sato, T.; Schweiger, P. Digital image analysis and chlorophyll metering for phenotyping the effects of nodulation in soybean. Comput. Electron. Agric. 2011, 75, 190–195. [Google Scholar]
- Atefi, A.; Ge, Y.; Pitla, S.; Schnable, J. In vivo human-like robotic phenotyping of leaf traits in maize and sorghum in greenhouse. Comput. Electron. Agric. 2019, 163, 104854. [Google Scholar] [CrossRef]
- Rorie, R.L.; Purcell, L.C.; Karcher, D.E.; King, C.A. The assessment of leaf nitrogen in corn from digital images. Crop. Sci. 2011, 51, 2174–2180. [Google Scholar] [CrossRef] [Green Version]
- Hassanijalilian, O.; Igathinathane, C.; Doetkott, C.; Bajwa, S.; Nowatzki, J.; Haji Esmaeili, S.A. Chlorophyll estimation in soybean leaves infield with smartphone digital imaging and machine learning. Comput. Electron. Agric. 2020, 174, 105433. [Google Scholar] [CrossRef]
- Smidt, E.R.; Conley, S.P.; Zhu, J.; Arriaga, F.J. Identifying Field Attributes that Predict Soybean Yield Using Random Forest Analysis. Agron. J. 2016, 108, 637–646. [Google Scholar] [CrossRef] [Green Version]
- Bakhshipour, A.; Jafari, A. Evaluation of support vector machine and artificial neural networks in weed detection using shape features. Comput. Electron. Agric. 2018, 145, 153–160. [Google Scholar] [CrossRef]
- Naik, H.S.; Zhang, J.; Lofquist, A.; Assefa, T.; Sarkar, S.; Ackerman, D.; Singh, A.; Singh, A.K.; Ganapathysubramanian, B. A real-time phenotyping framework using machine learning for plant stress severity rating in soybean. Plant Methods 2017, 13, 23. [Google Scholar] [CrossRef] [Green Version]
- Azadbakht, M.; Ashourloo, D.; Aghighi, H.; Radiom, S.; Alimohammadi, A. Wheat leaf rust detection at canopy scale under different LAI levels using machine learning techniques. Comput. Electron. Agric. 2019, 156, 119–128. [Google Scholar] [CrossRef]
- Yang, N.; Liu, D.; Feng, Q.; Xiong, Q.; Zhang, L.; Ren, T.; Zhao, Y.; Zhu, D.; Huang, J. Large-Scale Crop Mapping Based on Machine Learning and Parallel Computation with Grids. Remote Sens. 2019, 11, 1500. [Google Scholar] [CrossRef] [Green Version]
- Yu, N.; Li, L.; Schmitz, N.; Tian, L.F.; Greenberg, J.A.; Diers, B.W. Development of methods to improve soybean yield estimation and predict plant maturity with an unmanned aerial vehicle based platform. Remote Sens. Environ. 2016, 187, 91–101. [Google Scholar] [CrossRef]
- Bai, G.; Jenkins, S.; Yuan, W.; Graef, G.L.; Ge, Y. Field-based scoring of soybean iron deficiency chlorosis using RGB imaging and statistical learning. Front. Plant Sci. 2018, 9, 1002. [Google Scholar] [PubMed] [Green Version]
- MATLAB. Version 8.6 (R2015b); Image Processing Toolbox; The MathWorks Inc.: Natick, MA, USA, 2015. [Google Scholar]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [Green Version]
- Géron, A. Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’ Reilly Media, Inc.: Sebastopol, CA, USA, 2017. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Domingos, P. Metacost: A general method for making classifiers cost-sensitive. In Proceedings of the Fifth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 15–18 August 1999; Volume 99, pp. 155–164. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Fiore, U.; De Santis, A.; Perla, F.; Zanetti, P.; Palmieri, F. Using generative adversarial networks for improving classification effectiveness in credit card fraud detection. Inf. Sci. 2019, 479, 448–455. [Google Scholar] [CrossRef]
- Geetha, R.; Sivasubramanian, S.; Kaliappan, M.; Vimal, S.; Annamalai, S. Cervical Cancer Identification with Synthetic Minority Oversampling Technique and PCA Analysis using Random Forest Classifier. J. Med. Syst. 2019, 43, 286. [Google Scholar] [CrossRef]
- Espejo-Garcia, B.; Martinez-Guanter, J.; Pérez-Ruiz, M.; Lopez-Pellicer, F.J.; Zarazaga-Soria, F.J. Machine learning for automatic rule classification of agricultural regulations: A case study in Spain. Comput. Electron. Agric. 2018, 150, 343–352. [Google Scholar] [CrossRef]
- Aiken, V.C.F.; Dórea, J.R.R.; Acedo, J.S.; de Sousa, F.G.; Dias, F.G.; de Magalhães Rosa, G.J. Record linkage for farm-level data analytics: Comparison of deterministic, stochastic and machine learning methods. Comput. Electron. Agric. 2019, 163, 104857. [Google Scholar] [CrossRef]
- Shahriar, M.S.; Rahman, A.; McCulloch, J. Predicting shellfish farm closures using time series classification for aquaculture decision support. Comput. Electron. Agric. 2014, 102, 85–97. [Google Scholar] [CrossRef]
- Louppe, G.; Wehenkel, L.; Sutera, A.; Geurts, P. Understanding variable importances in forests of randomized trees. Adv. Neural Inf. Process. Syst. 2013, 26, 431–439. [Google Scholar]
- Rehman, T.U.; Mahmud, M.S.; Chang, Y.K.; Jin, J.; Shin, J. Current and future applications of statistical machine learning algorithms for agricultural machine vision systems. Comput. Electron. Agric. 2019, 156, 585–605. [Google Scholar] [CrossRef]










| IDC Symptoms Description | IDC Score |
|---|---|
| No chlorosis | 1 |
| Slight yellowing of the upper leaves | 2 |
| Upper leaves without necrosis or stunting and with interveinal chlorosis | 3 |
| Upper leaves with reduced growth or beginning of necrosis with interveinal chlorosis | 4 |
| Severe stunting, damaged to growing point and chlorosis | 5 |
| Model | MR | Visual | Date 1 (3 July 2014) | Date 2 (17 July 2014) | ||||
|---|---|---|---|---|---|---|---|---|
| Score | Precision | Recall | f1-Score | Precision | Recall | f1-Score | ||
| Decision Tree | 1 | 1.0 | 0.67 | 0.74 | 0.70 | 0.79 | 0.85 | 0.81 |
| 2 | 1.5–2.0 | 0.38 | 0.26 | 0.31 | 0.46 | 0.46 | 0.46 | |
| 3 | 2.5–3.0 | 0.58 | 0.70 | 0.64 | 0.50 | 0.43 | 0.46 | |
| 4 | 3.5–4.0 | - | - | - | 0.86 | 0.92 | 0.89 | |
| Average | 0.54 | 0.57 | 0.55 | 0.65 | 0.66 | 0.66 | ||
| Random Forest | 1 | 1.0 | 0.71 | 0.79 | 0.75 | 0.79 | 0.85 | 0.81 |
| 2 | 1.5–2.0 | 0.80 | 0.42 | 0.55 | 0.50 | 0.38 | 0.43 | |
| 3 | 2.5–3.0 | 0.70 | 0.95 | 0.81 | 0.54 | 0.50 | 0.52 | |
| 4 | 3.5–4.0 | - | - | - | 0.81 | 1.00 | 0.90 | |
| Average | 0.74 | 0.72 | 0.70 | 0.66 | 0.68 | 0.67 | ||
| AdaBoost | 1 | 1.0 | 0.78 | 0.95 | 0.86 | 0.80 | 0.92 | 0.86 |
| 2 | 1.5–2.0 | 0.73 | 0.58 | 0.65 | 0.56 | 0.38 | 0.45 | |
| 3 | 2.5–3.0 | 0.85 | 0.85 | 0.85 | 0.60 | 0.64 | 0.62 | |
| 4 | 3.5–4.0 | - | - | - | 0.93 | 1.00 | 0.96 | |
| Average | 0.79 | 0.79 | 0.78 | 0.72 | 0.74 | 0.72 | ||
| Feature | Mean Decrease Impurity Factor | ||||||
|---|---|---|---|---|---|---|---|
| Date 1 (3 July 2014) | Date 2 (17 July 2014) | Mean * | |||||
| DT | RF | AdaBoost | DT | RF | AdaBoost | ||
| 0.41 | 0.28 | 0.14 | 0.51 | 0.28 | 0.22 | 0.31 | |
| 0.11 | 0.15 | 0.14 | 0.00 | 0.01 | 0.03 | 0.07 | |
| 0.03 | 0.11 | 0.20 | 0.22 | 0.16 | 0.24 | 0.16 | |
| 0.09 | 0.09 | 0.08 | 0.00 | 0.09 | 0.05 | 0.07 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | |
| Canopy Size | 0.35 | 0.16 | 0.26 | 0.26 | 0.22 | 0.32 | 0.26 |
| Average DGCI | 0.00 | 0.14 | 0.05 | 0.00 | 0.17 | 0.09 | 0.08 |
| SD DGCI | 0.00 | 0.08 | 0.13 | 0.01 | 0.06 | 0.03 | 0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassanijalilian, O.; Igathinathane, C.; Bajwa, S.; Nowatzki, J. Rating Iron Deficiency in Soybean Using Image Processing and Decision-Tree Based Models. Remote Sens. 2020, 12, 4143. https://doi.org/10.3390/rs12244143
Hassanijalilian O, Igathinathane C, Bajwa S, Nowatzki J. Rating Iron Deficiency in Soybean Using Image Processing and Decision-Tree Based Models. Remote Sensing. 2020; 12(24):4143. https://doi.org/10.3390/rs12244143
Chicago/Turabian StyleHassanijalilian, Oveis, C. Igathinathane, Sreekala Bajwa, and John Nowatzki. 2020. "Rating Iron Deficiency in Soybean Using Image Processing and Decision-Tree Based Models" Remote Sensing 12, no. 24: 4143. https://doi.org/10.3390/rs12244143
APA StyleHassanijalilian, O., Igathinathane, C., Bajwa, S., & Nowatzki, J. (2020). Rating Iron Deficiency in Soybean Using Image Processing and Decision-Tree Based Models. Remote Sensing, 12(24), 4143. https://doi.org/10.3390/rs12244143