Estimating the Leaf Nitrogen Content with a New Feature Extracted from the Ultra-High Spectral and Spatial Resolution Images in Wheat
Abstract
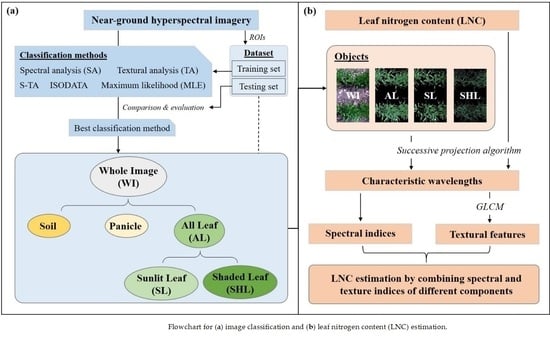
:1. Introduction
2. Materials and Methods
2.1. Experimental Design and LNC Measurements
2.2. Near-Ground Hyperspectral Imagery
2.2.1. Data Acquisition
2.2.2. Data Preprocessing
2.3. Image Classification
2.3.1. Spectral Analysis (SA)
2.3.2. Textural Analysis (TA)
2.3.3. Comparison and Evaluation
2.4. LNC Estimation
2.4.1. Selection of Characteristic Wavelengths
2.4.2. Calculation of Textural Features
2.4.3. Spectral and Textural Indices
2.4.4. Estimation and Validation
3. Results
3.1. Near-Ground Hyperspectral Image Classification
3.2. Changes in Reflectance of Different Objects under Different Conditions
3.3. LNC Estimation Using Spectral and Texture Indices of Different Objects
4. Discussion
4.1. Assessment of Classification Methods
4.2. Soil Background and Shadow Effects in LNC Estimation
4.3. Further Improvement of the LNC Estimation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Benedetti, R.; Rossini, P. On the use of NDVI profiles as a tool for agricultural statistics: The case study of wheat yield estimate and forecast in Emilia Romagna. Remote Sens. Environ. 1993, 45, 311–326. [Google Scholar] [CrossRef]
- Jiang, J.; Cai, W.; Zheng, H.; Cheng, T.; Tian, Y.; Zhu, Y.; Ehsani, R.; Hu, Y.; Niu, Q.; Gui, L. Using Digital Cameras on an Unmanned Aerial Vehicle to Derive Optimum Color Vegetation Indices for Leaf Nitrogen Concentration Monitoring in Winter Wheat. Remote Sens. 2019, 11, 2667. [Google Scholar] [CrossRef] [Green Version]
- Fitzgerald, G.; Rodriguez, D.; Leary, O.G. Measuring and predicting canopy nitrogen nutrition in wheat using a spectral index—The canopy chlorophyll content index (CCCI). Field Crop. Res. 2010, 116, 318–324. [Google Scholar] [CrossRef]
- Hansen, P.; Schjoerring, J. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Li, D.; Wang, X.; Zheng, H.; Zhou, K.; Yao, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cheng, T. Estimation of area-and mass-based leaf nitrogen contents of wheat and rice crops from water-removed spectra using continuous wavelet analysis. Plant Methods 2018, 14, 76. [Google Scholar] [CrossRef]
- Zheng, H.; Cheng, T.; Li, D.; Zhou, X.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Evaluation of RGB, color-infrared and multispectral images acquired from unmanned aerial systems for the estimation of nitrogen accumulation in rice. Remote Sens. 2018, 10, 824. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Miao, Y.; Cao, Q.; Wang, H.; Gnyp, M.L.; Bareth, G.; Khosla, R.; Yang, W.; Liu, F.; Liu, C. In-season estimation of rice nitrogen status with an active crop canopy sensor. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4403–4413. [Google Scholar] [CrossRef]
- Yao, X.; Zhu, Y.; Tian, Y.; Feng, W.; Cao, W. Exploring hyperspectral bands and estimation indices for leaf nitrogen accumulation in wheat. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 89–100. [Google Scholar] [CrossRef]
- Feng, W.; Yao, X.; Zhu, Y.; Tian, Y.; Cao, W. Monitoring leaf nitrogen status with hyperspectral reflectance in wheat. Eur. J. Agron. 2008, 28, 394–404. [Google Scholar] [CrossRef]
- Yao, X.; Ren, H.; Cao, Z.; Tian, Y.; Cao, W.; Zhu, Y.; Cheng, T. Detecting leaf nitrogen content in wheat with canopy hyperspectrum under different soil backgrounds. Int. J. Appl. Earth Obs. Geoinf. 2014, 32, 114–124. [Google Scholar] [CrossRef]
- Li, F.; Mistele, B.; Hu, Y.; Chen, X.; Schmidhalter, U. Reflectance estimation of canopy nitrogen content in winter wheat using optimised hyperspectral spectral indices and partial least squares regression. Eur. J. Agron. 2014, 52, 198–209. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, H.; Wang, P. Quantitative modelling for leaf nitrogen content of winter wheat using UAV-based hyperspectral data. Int. J. Remote Sens. 2017, 38, 2117–2134. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Tejada, Z.P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Vigneau, N.; Ecarnot, M.; Rabatel, G.; Roumet, P. Potential of field hyperspectral imaging as a non destructive method to assess leaf nitrogen content in Wheat. Field Crop. Res. 2011, 122, 25–31. [Google Scholar] [CrossRef] [Green Version]
- Onoyama, H.; Ryu, C.; Suguri, M.; Iida, M. Nitrogen prediction model of rice plant at panicle initiation stage using ground-based hyperspectral imaging: Growing degree-days integrated model. Precis. Agric. 2015, 16, 558–570. [Google Scholar] [CrossRef]
- Jay, S.; Hadoux, X.; Gorretta, N.; Rabatel, G. Potential of Hyperspectral Imagery for Nitrogen Content Retrieval in Sugar Beet Leaves; AgEng: Évora, Portugal, 2014. [Google Scholar]
- Miphokasap, P.; Honda, K.; Vaiphasa, C.; Souris, M.; Nagai, M. Estimating canopy nitrogen concentration in sugarcane using field imaging spectroscopy. Remote Sens. 2012, 4, 1651–1670. [Google Scholar] [CrossRef] [Green Version]
- Zhou, K.; Cheng, T.; Zhu, Y.; Cao, W.; Ustin, S.L.; Zheng, H.; Yao, X.; Tian, Y. Assessing the Impact of Spatial Resolution on the Estimation of Leaf Nitrogen Concentration Over the Full Season of Paddy Rice Using Near-Surface Imaging Spectroscopy Data. Front. Plant Sci. 2018, 9, 964. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adeline, K.; Chen, M.; Briottet, X.; Pang, S.; Paparoditis, N. Shadow detection in very high spatial resolution aerial images: A comparative study. ISPRS J. Photogramm. Remote Sens. 2013, 80, 21–38. [Google Scholar] [CrossRef]
- Zhou, K.; Deng, X.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y.; Ustin, S.L.; Cheng, T. Assessing the Spectral Properties of Sunlit and Shaded Components in Rice Canopies with Near-Ground Imaging Spectroscopy Data. Sensors 2017, 17, 578. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, K.; Krishnan, P. Normalized Sunlit Shaded Index (NSSI) for characterizing the moisture stress in wheat crop using classified thermal and visible images. Ecol. Indic. 2020, 110. [Google Scholar] [CrossRef]
- Dongyan, Z. Diagnosis Mechanism and Methods of Crop Chlorophyll Information Based on Hypersepctral Imaging Technology; Zhejiang University: Hangzhou, China, 2012. (in Chinese) [Google Scholar]
- Gnyp, M.L.; Miao, Y.; Yuan, F.; Ustin, S.L.; Yu, K.; Yao, Y.; Huang, S.; Bareth, G. Hyperspectral canopy sensing of paddy rice aboveground biomass at different growth stages. Field Crop. Res. 2014, 155, 42–55. [Google Scholar] [CrossRef]
- Bharati, M.H.; Liu, J.J.; MacGregor, J.F. Image texture analysis: Methods and comparisons. Chemom. Intell. Lab. Syst. 2004, 72, 57–71. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef] [Green Version]
- Haralick, R.M. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Lu, D.; Batistella, M. Exploring TM image texture and its relationships with biomass estimation in Rondônia, Brazilian Amazon. Acta Amaz. 2005, 35, 249–257. [Google Scholar] [CrossRef]
- Zheng, H.; Ma, J.; Zhou, M.; Li, D.; Yao, X.; Cao, W.; Zhu, Y.; Cheng, T. Enhancing the Nitrogen Signals of Rice Canopies across Critical Growth Stages through the Integration of Textural and Spectral Information from Unmanned Aerial Vehicle (UAV) Multispectral Imagery. Remote Sens. 2020, 12, 957. [Google Scholar] [CrossRef] [Green Version]
- Ashoori, H.; Fahimnejad, H.; Alimohammadi, A.; Soofbaf, S. Evaluation of the usefulness of texture measures for crop type classification by Hyperion data. Int. Arch. Spat. Inf. Sci. 2008, 37, 999–1006. [Google Scholar]
- Rellier, G.; Descombes, X.; Falzon, F.; Zerubia, J. Texture feature analysis using a Gauss-Markov model in hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1543–1551. [Google Scholar] [CrossRef]
- Qian, Y.; Ye, M.; Zhou, J. Hyperspectral image classification based on structured sparse logistic regression and three-dimensional wavelet texture features. IEEE Trans. Geosci. Remote Sens. 2012, 51, 2276–2291. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Sun, Y.; Shang, K.; Zhang, L.; Wang, S. Crop classification based on feature band set construction and object-oriented approach using hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4117–4128. [Google Scholar] [CrossRef]
- Zheng, H.; Cheng, T.; Zhou, M.; Li, D.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Improved estimation of rice aboveground biomass combining textural and spectral analysis of UAV imagery. Precis. Agric. 2018, 20, 611–629. [Google Scholar] [CrossRef]
- Yue, J.; Yang, G.; Tian, Q.; Feng, H.; Xu, K.; Zhou, C. Estimate of winter-wheat above-ground biomass based on UAV ultrahigh-ground-resolution image textures and vegetation indices. ISPRS J. Photogramm. Remote Sens. 2019, 150, 226–244. [Google Scholar] [CrossRef]
- Li, S.; Yuan, F.; Karim, A.U.S.T.; Zheng, H.; Cheng, T.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cao, Q. Combining Color Indices and Textures of UAV-Based Digital Imagery for Rice LAI Estimation. Remote Sens. 2019, 11, 1763. [Google Scholar] [CrossRef] [Green Version]
- Dube, T.; Mutanga, O. Investigating the robustness of the new Landsat-8 Operational Land Imager derived texture metrics in estimating plantation forest aboveground biomass in resource constrained areas. ISPRS J. Photogramm. Remote Sens. 2015, 108, 12–32. [Google Scholar] [CrossRef]
- Yang, W.H.; Peng, S.; Huang, J.; Sanico, A.L.; Buresh, R.J.; Witt, C. Using leaf color charts to estimate leaf nitrogen status of rice. Agron. J. 2003, 95, 212–217. [Google Scholar]
- Singh, B.; Singh, Y.; Ladha, J.K.; Bronson, K.F.; Balasubramanian, V.; Singh, J.; Khind, C.S. Chlorophyll meter–and leaf color chart–based nitrogen management for rice and wheat in Northwestern India. Agron. J. 2002, 94, 821–829. [Google Scholar] [CrossRef]
- Da Silva Oliveira, M.W. Texture Analysis on Leaf Images for Early Nutritional Diagnosis in Maize Culture; University of São Paulo: São Paulo, Brazil, 2016. [Google Scholar]
- Romualdo, L.; Luz, P.; Devechio, F.; Marin, M.; Zúñiga, A.; Bruno, O.; Herling, V. Use of artificial vision techniques for diagnostic of nitrogen nutritional status in maize plants. Comput. Electron. Agric. 2014, 104, 63–70. [Google Scholar] [CrossRef]
- Kimes, D.; Newcomb, W.; Tucker, C.; Zonneveld, I.; Van Wijngaarden, W.; De Leeuw, J.; Epema, G. Directional reflectance factor distributions for cover types of Northern Africa. Remote Sens. Environ. 1985, 18, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Leblanc, S.G.; Chen, J.M.; Cihlar, J. NDVI directionality in boreal forests: A model interpretation of measurements. Canadian J. Remote Sens. 1997, 23, 369–380. [Google Scholar] [CrossRef]
- Sun, H.; Li, M.Z.; Zhao, Y.; Zhang, Y.E.; Wang, X.M.; Li, X.H. The spectral characteristics and chlorophyll content at winter wheat growth stages. Spectrosc. Spectr. Anal. 2010, 30, 192–196. [Google Scholar]
- Yue, J.; Feng, H.; Yang, G.; Li, Z. A comparison of regression techniques for estimation of above-ground winter wheat biomass using near-surface spectroscopy. Remote Sens. 2018, 10, 66. [Google Scholar] [CrossRef] [Green Version]
- Bremner, J.M.; Mulvaney, C. Nitrogen—total. Methods Soil Anal. Part. 2 Chem. Microbiol. Prop. 1983, 9, 595–624. [Google Scholar]
- Haralick, R.M.; Sternberg, S.R.; Zhuang, X. Image analysis using mathematical morphology. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 4, 532–550. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Trinder, J.C.; Niu, R. Object-oriented landslide mapping using ZY-3 satellite imagery, random forest and mathematical morphology, for the Three-Gorges Reservoir, China. Remote Sens. 2017, 9, 333. [Google Scholar] [CrossRef] [Green Version]
- Ghamisi, P.; Maggiori, E.; Li, S.; Souza, R.; Tarablaka, Y.; Moser, G.; De Giorgi, A.; Fang, L.; Chen, Y.; Chi, M. New frontiers in spectral-spatial hyperspectral image classification: The latest advances based on mathematical morphology, Markov random fields, segmentation, sparse representation, and deep learning. IEEE Geosci. Remote Sens. Mag. 2018, 6, 10–43. [Google Scholar] [CrossRef]
- Abbas, A.W.; Minallh, N.; Ahmad, N.; Abid, S.A.R.; Khan, M.A.A. K-Means and ISODATA Clustering Algorithms for Landcover Classification Using Remote Sensing. 2016, Volume 48. ISSN 1813-1743. Available online: https://sujo-old.usindh.edu.pk/index.php/SURJ/article/view/2358 (accessed on 5 January 2021).
- Hemalatha, S.; Anouncia, S.M. Unsupervised segmentation of remote sensing images using FD based texture analysis model and ISODATA. Int. J. Ambient Comput. Intell. (IJACI) 2017, 8, 58–75. [Google Scholar] [CrossRef]
- Peng, J.; Li, L.; Tang, Y.Y. Maximum likelihood estimation-based joint sparse representation for the classification of hyperspectral remote sensing images. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 1790–1802. [Google Scholar] [CrossRef]
- Strahler, A.H. The use of prior probabilities in maximum likelihood classification of remotely sensed data. Remote Sens. Environ. 1980, 10, 135–163. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Araújo, M.C.U.; Saldanha, T.C.B.; Galvao, R.K.H.; Yoneyama, T.; Chame, H.C.; Visani, V. The successive projections algorithm for variable selection in spectroscopic multicomponent analysis. Chemom. Intell. Lab. Syst. 2001, 57, 65–73. [Google Scholar] [CrossRef]
- Wang, Y.J.; Li, L.Q.; Shen, S.S.; Liu, Y.; Ning, J.M.; Zhang, Z.Z. Rapid detection of quality index of postharvest fresh tea leaves using hyperspectral imaging. J. Sci. Food Agric. 2020, 100, 3803–3811. [Google Scholar] [CrossRef] [PubMed]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Malenovský, Z.; Homolová, L.; Milla, Z.R.; Lukeš, P.; Kaplan, V.; Hanuš, J.; Etchegorry, G.J.P.; Schaepman, M.E. Retrieval of spruce leaf chlorophyll content from airborne image data using continuum removal and radiative transfer. Remote Sens. Environ. 2013, 131, 85–102. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Chen, J.M.; Miller, J.R.; Noland, T.L. Leaf chlorophyll content retrieval from airborne hyperspectral remote sensing imagery. Remote Sens. Environ. 2008, 112, 3234–3247. [Google Scholar] [CrossRef]
- Tejada, Z.P.J.; Miller, J.R.; Harron, J.; Hu, B.; Noland, T.L.; Goel, N.; Mohammed, G.H.; Sampson, P. Needle chlorophyll content estimation through model inversion using hyperspectral data from boreal conifer forest canopies. Remote Sens. Environ. 2004, 89, 189–199. [Google Scholar] [CrossRef]
- Chen, J.M.; Leblanc, S.G. Multiple-scattering scheme useful for geometric optical modeling. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1061–1071. [Google Scholar] [CrossRef]
- Zhou, K.; Guo, Y.; Geng, Y.; Zhu, Y.; Cao, W.; Tian, Y. Development of a novel bidirectional canopy reflectance model for row-planted rice and wheat. Remote Sens. 2014, 6, 7632–7659. [Google Scholar] [CrossRef] [Green Version]
- Kokaly, R.F.; Despain, D.G.; Clark, R.N.; Livo, K.E. Mapping vegetation in Yellowstone National Park using spectral feature analysis of AVIRIS data. Remote Sens. Environ. 2003, 84, 437–456. [Google Scholar] [CrossRef] [Green Version]
- Salisbury, J.W.; Milton, N.; Walsh, P. Significance of non-isotropic scattering from vegetation for geobotanical remote sensing. Int. J. Remote Sens. 1987, 8, 997–1009. [Google Scholar] [CrossRef]
- Baret, F.; Jacquemoud, S.; Guyot, G.; Leprieur, C. Modeled analysis of the biophysical nature of spectral shifts and comparison with information content of broad bands. Remote Sens. Environ. 1992, 41, 133–142. [Google Scholar] [CrossRef]
- Chen, D.; Stow, D.; Gong, P. Examining the effect of spatial resolution and texture window size on classification accuracy: An urban environment case. Int. J. Remote Sens. 2004, 25, 2177–2192. [Google Scholar] [CrossRef]
- Ning, S. Remote sensing image texture analysis and fractal assessment. J. Wuhan Tech. Univ. Surv. Mapp. 1998, 23, 370–373. [Google Scholar]
- Lu, D. Aboveground biomass estimation using Landsat TM data in the Brazilian Amazon. Int. J. Remote Sens. 2005, 26, 2509–2525. [Google Scholar] [CrossRef]
- Hall, O.; Dahlin, S.; Marstorp, H.; Archila Bustos, M.F.; Öborn, I.; Jirström, M. Classification of maize in complex smallholder farming systems using UAV imagery. Drones 2018, 2, 22. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Zang, S.; Zhang, B.; Li, S.; Wu, C. A review of remote sensing image classification techniques: The role of spatio-contextual information. Eur. J. Remote Sens. 2014, 47, 389–411. [Google Scholar] [CrossRef]







| Trials | Year | Variety | Planting Density (plants/ha) | Nitrogen Rate (kg/ha) | Sowing Date | Sampling Stage |
|---|---|---|---|---|---|---|
| Exp. 1 | 2012–2013 | V1: Yangmai 18 V2: Shengxuan 6 | D1: 150 D2: 300 | N0: 0 N1: 150 N2: 300 | 5 November 2012 | Greening Jointing Booting Heading |
| Exp. 2 | 2013–2014 | V1: Yangmai 18 V2: Shengxuan 6 | D1: 150 D2: 300 | N0: 0 N1: 150 N2: 300 | 28 October 2013 | Greening Jointing Booting Heading |
| Textural Feature | Formula 1 | Description | Example |
|---|---|---|---|
| Mean (ME) | A measure of the degree of texture rules |  | |
| Variance (VA) | A measure of the dispersion of the values around the mean |  | |
| Correlation (CC) | A measure of how correlated a pixel is to its neighbor over the whole image |  | |
| Homogeneity (HO) | A measure of the local uniformity of a pixel pair |  | |
| Contrast (CO) | A measure of the local variations presented in an image |  | |
| Dissimilarity (DI) | A measure of the mean of the gray-level difference distribution of an image |  | |
| Entropy (EN) | A measure of randomness degree of an image texture |  | |
| Second moment (SM) | A measure of global homogeneity of an image |  |
| Target Component | Threshold | Greening | Jointing | Booting | Heading | All Stages |
|---|---|---|---|---|---|---|
| Soil | Min | −2.663 | −3.742 | −2.438 | −1.414 | −3.742 |
| Max | 0.072 | 0.272 | 0.108 | 0.188 | 0.272 | |
| SHL | Min | 0.303 | 0.602 | 0.596 | 0.522 | 0.303 |
| Max | 1.411 | 2.009 | 2.063 | 2.072 | 2.072 | |
| SL | Min | 2.203 | 2.215 | 3.250 | 2.980 | 2.203 |
| Max | 9.795 | 9.865 | 9.794 | 9.444 | 9.865 | |
| Panicle | Min | — | — | — | −3.886 | −3.886 |
| Max | — | — | — | 8.104 | 8.104 |
| Target Class | Method | SL | SHL | Panicle | Soil |
|---|---|---|---|---|---|
| SL | ISODATA | 96.58 | 0 | 3.42 | 0 |
| MLE | 98.49 | 0 | 1.51 | 0 | |
| SA | 91.06 | 0 | 8.94 | 0 | |
| TA | 80.43 | 17.54 | 2.03 | 0 | |
| S-TA | 99.34 | 0 | 0.66 | 0 | |
| SHL | ISODATA | 0.40 | 27.57 | 34.07 | 37.97 |
| MLE | 0 | 90.09 | 0 | 9.91 | |
| SA | 0 | 89.20 | 10.80 | 0 | |
| TA | 6.23 | 93.37 | 0.40 | 0 | |
| S-TA | 0 | 98.92 | 1.08 | 0 | |
| Panicle | ISODATA | 52.35 | 35.81 | 11.85 | 0 |
| MLE | 2.32 | 5.81 | 91.86 | 0 | |
| SA | 18.86 | 30.35 | 48.50 | 2.28 | |
| TA | 7.38 | 0.72 | 91.91 | 0 | |
| S-TA | 0 | 0 | 100 | 0 | |
| Soil | ISODATA | 0 | 0 | 0.21 | 99.79 |
| MLE | 0 | 0.02 | 0 | 99.98 | |
| SA | 0 | 0 | 0 | 100 | |
| TA | 0 | 0 | 0 | 100 | |
| S-TA | 0 | 0 | 0 | 100 |
| Method | Overall Accuracy (%) | Kappa Coefficient | Run Time (min) |
|---|---|---|---|
| ISODATA | 71.6 | 0.632 | 85 |
| MLE | 94.5 | 0.942 | 100 |
| SA | 89.4 | 0.866 | 6 |
| TA | 89.6 | 0.868 | 12 |
| S-TA | 97.8 | 0.971 | 14 |
| Object | Characteristic Wavelength (nm) 1 |
|---|---|
| WI | 537.46, 479.26, 732.78, 400.49, 931.88, 945.34 |
| AL | 688.72, 758.28, 810.48, 931.88, 432.28, 664.39 |
| SL | 723.46, 457.03, 690.16, 400.49, 945.21 |
| SHL | 759.68, 696.42, 550.36, 840.38, 412.49, 933.21 |
| WI | 537.46, 479.26, 732.78, 400.49, 931.88, 945.34 |
| Object | Index 1 | RRMSEc (%) | RRMSEv (%) | ||
|---|---|---|---|---|---|
| WI | RSI (R945.34, R537.46) | 0.64 | 16.3 | 0.54 | 17.8 |
| NDTI (T400.49ME, T945.34EN) | 0.40 | 18.4 | 0.41 | 23.2 | |
| NDSTI (R931.88, T931.88EN) | 0.66 | 15.9 | 0.67 | 14.4 | |
| AL | DSI (R688.72, R432.38) | 0.75 | 13.9 | 0.66 | 16.2 |
| RTI (T810.48HO, T931.88ME) | 0.70 | 14.4 | 0.73 | 13.6 | |
| NDSTI (R931.88, T432.38SM) | 0.78 | 13.5 | 0.83 | 10.9 | |
| SL | NDSI (R945.21, R723.46) | 0.50 | 15.2 | 0.49 | 18.0 |
| NDTI (T945.21DI, T690.16SM) | 0.27 | 19.0 | 0.33 | 19.9 | |
| NDSTI (R945.21, T945.21SM) | 0.53 | 15.4 | 0.52 | 17.0 | |
| SHL | NDSI (R696.42, R412.49) | 0.52 | 15.4 | 0.27 | 23.1 |
| NDTI (T933.21ME, T696.42SM) | 0.34 | 17.9 | 0.39 | 21.8 | |
| NDSTI (R933.21, T933.21SM) | 0.49 | 16.1 | 0.46 | 17.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Zhu, J.; Wang, X.; Cheng, T.; Tian, Y.; Zhu, Y.; Cao, W.; Yao, X. Estimating the Leaf Nitrogen Content with a New Feature Extracted from the Ultra-High Spectral and Spatial Resolution Images in Wheat. Remote Sens. 2021, 13, 739. https://doi.org/10.3390/rs13040739
Jiang J, Zhu J, Wang X, Cheng T, Tian Y, Zhu Y, Cao W, Yao X. Estimating the Leaf Nitrogen Content with a New Feature Extracted from the Ultra-High Spectral and Spatial Resolution Images in Wheat. Remote Sensing. 2021; 13(4):739. https://doi.org/10.3390/rs13040739
Chicago/Turabian StyleJiang, Jiale, Jie Zhu, Xue Wang, Tao Cheng, Yongchao Tian, Yan Zhu, Weixing Cao, and Xia Yao. 2021. "Estimating the Leaf Nitrogen Content with a New Feature Extracted from the Ultra-High Spectral and Spatial Resolution Images in Wheat" Remote Sensing 13, no. 4: 739. https://doi.org/10.3390/rs13040739
APA StyleJiang, J., Zhu, J., Wang, X., Cheng, T., Tian, Y., Zhu, Y., Cao, W., & Yao, X. (2021). Estimating the Leaf Nitrogen Content with a New Feature Extracted from the Ultra-High Spectral and Spatial Resolution Images in Wheat. Remote Sensing, 13(4), 739. https://doi.org/10.3390/rs13040739