Mapping Forest Composition with Landsat Time Series: An Evaluation of Seasonal Composites and Harmonic Regression
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Forest Reference Data
2.3. Digital Data Acquisition and Processing
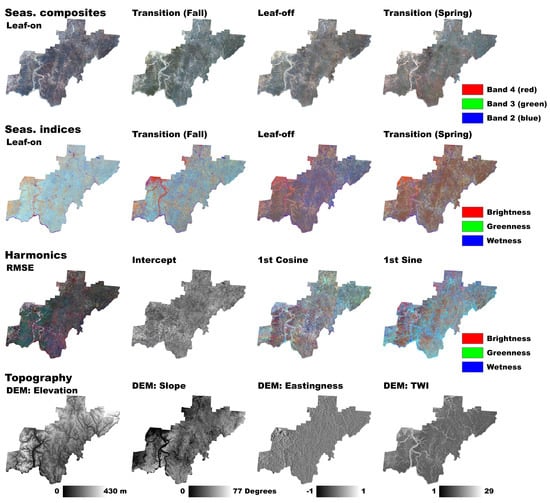
2.3.1. Composite Images
2.3.2. Time Series Modeling
2.3.3. Environmental Variables
2.4. Data Analysis
2.4.1. Forest-Type Grouping
2.4.2. Compositional Ordination
2.4.3. Compositional Modeling
2.5. Agreement Assessment
2.6. Feature Importance Assessment
2.7. Mapping Output
3. Results
3.1. Compositional Attributes
3.2. Feature Set Agreement
3.3. Forest Type Agreement
3.4. Feature Importance
3.5. Compositional Maps
4. Discussion
4.1. Forest Type Classification
4.2. Gradient Modeling
4.3. Time Series Processing, Applications, and Future Directions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wulder, M.A.; Coops, N.C.; Roy, D.P.; White, J.C.; Hermosilla, T. Land cover 2.0. Int. J. Remote Sens. 2018, 39, 4254–4284. [Google Scholar] [CrossRef] [Green Version]
- Cohen, W.B.; Goward, S.N. Landsat’s role in ecological applications of remote sensing. Bioscience 2006, 54, 535–545. [Google Scholar] [CrossRef]
- Iverson, L.R.; Graham, R.L.; Cook, E.A. Applications of satellite remote sensing to forested ecosystems. Landsc. Ecol. 1989, 3, 131–143. [Google Scholar] [CrossRef]
- Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the archive: How free data has enabled the science and monitoring promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
- He, H.S.; Mladenoff, D.J.; Radeloff, V.C.; Crow, T.R. Integration of GIS data and classified satellite imagery for regional forest assessment. Ecol. Appl. 1998, 8, 1072–1083. [Google Scholar] [CrossRef]
- Kerr, J.T.; Ostrovsky, M. From space to species: Ecological applications for remote sensing. Trends Ecol. Evol. 2003, 18, 299–305. [Google Scholar] [CrossRef]
- Perera, A.H.; Peterson, U.; Pastur, G.M.; Iverson, L.R. Ecosystem Services from Forest Landscapes: Broadscale Considerations; Springer: Cham, Switzerland, 2018; pp. 1–265. [Google Scholar]
- Tilman, D.; Knops, J.; Wedin, D.; Reich, P.; Ritchie, M.; Siemann, E. The influence of functional diversity and composition on ecosystem processes. Science 1997, 277, 1300–1302. [Google Scholar] [CrossRef] [Green Version]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef] [Green Version]
- White, J.C.; Wulder, M.A.; Hobart, G.W.; Luther, J.E.; Hermosilla, T.; Griffiths, P.; Coops, N.C.; Hall, R.J.; Hostert, P.; Dyk, A.; et al. Pixel-based image compositing for large-area dense time series applications and science. Can. J. Remote Sens. 2014, 40, 192–212. [Google Scholar] [CrossRef] [Green Version]
- McRoberts, R.E.; Cohen, W.B.; Erik, N.; Stehman, S.V.; Tomppo, E.O. Using remotely sensed data to construct and assess forest attribute maps and related spatial products. Scand. J. For. Res. 2010, 25, 340–367. [Google Scholar] [CrossRef]
- Dymond, C.C.; Mladenoff, D.J.; Radeloff, V.C. Phenological differences in Tasseled Cap indices improve deciduous forest classification. Remote Sens. Environ. 2002, 80, 460–472. [Google Scholar] [CrossRef]
- Wolter, P.T.; Mladenoff, D.J.; Host, G.E.; Crow, T.R. Improved forest classification in the northern Lake States using multi-temporal Landsat imagery. Photogramm. Eng. Remote Sens. 1995, 61, 1129–1143. [Google Scholar]
- Zhu, X.; Liu, D. Accurate mapping of forest types using dense seasonal landsat time-series. ISPRS J. Photogramm. Remote Sens. 2014, 96, 1–11. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Allen, R.; Anderson, M.; Belward, A.; Bindschadler, R.; Cohen, W.; Gao, F.; Goward, S.N.; Helder, D.; Helmer, E.; et al. Free access to Landsat Imagery. Science 2008, 320, 1011. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, R.E.; Andréfouët, S.; Cohen, W.B.; Gómez, C.; Griffiths, P.; Hais, M.; Healey, S.P.; Helmer, E.H.; Hostert, P.; Lyons, M.B.; et al. Bringing an ecological view of change to Landsat-based remote sensing. Front. Ecol. Environ. 2014, 12, 339–346. [Google Scholar] [CrossRef]
- Pasquarella, V.J.; Holden, C.E.; Kaufman, L.; Woodcock, C.E. From imagery to ecology: Leveraging time series of all available Landsat observations to map and monitor ecosystem state and dynamics. Remote Sens. Ecol. Conserv. 2016, 2, 152–170. [Google Scholar] [CrossRef]
- Banskota, A.; Kayastha, N.; Falkowski, M.J.; Wulder, M.A.; Froese, R.E.; White, J.C. Forest monitoring using Landsat time series data: A review. Can. J. Remote Sens. 2014, 40, 362–384. [Google Scholar] [CrossRef]
- Brooks, E.B.; Thomas, V.A.; Wynne, R.H.; Coulston, J.W. Fitting the multitemporal curve: A fourier series approach to the missing data problem in remote sensing analysis. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3340–3353. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.; Woodcock, C.E.; Holden, C.; Yang, Z. Generating synthetic Landsat images based on all available Landsat data: Predicting Landsat surface reflectance at any given time. Remote Sens. Environ. 2015, 162, 67–83. [Google Scholar] [CrossRef]
- Wang, S.; Azzari, G.; Lobell, D.B. Crop type mapping without field-level labels: Random forest transfer and unsupervised clustering techniques. Remote Sens. Environ. 2019, 222, 303–317. [Google Scholar] [CrossRef]
- Shimizu, K.; Ota, T.; Mizoue, N. Detecting forest changes using dense Landsat 8 and Sentinel-1 time series data in tropical seasonal forests. Remote Sens. 2019, 11, 1899. [Google Scholar] [CrossRef] [Green Version]
- Pasquarella, V.J.; Holden, C.E.; Woodcock, C.E. Improved mapping of forest type using spectral-temporal Landsat features. Remote Sens. Environ. 2018, 210, 193–207. [Google Scholar] [CrossRef]
- Wilson, B.T.; Knight, J.F.; McRoberts, R.E. Harmonic regression of Landsat time series for modeling attributes from national forest inventory data. ISPRS J. Photogramm. Remote Sens. 2018, 137, 29–46. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Midekisa, A.; Holl, F.; Savory, D.J.; Andrade-Pacheco, R.; Gething, P.W.; Bennett, A.; Sturrock, H.J.W. Mapping land cover change over continental Africa using Landsat and Google Earth Engine cloud computing. PLoS ONE 2017, 12, e0184926. [Google Scholar] [CrossRef] [PubMed]
- Hill, R.A.; Thompson, A.G. Mapping woodland species composition and structure using airborne spectral and LIDAR data. Int. J. Remote Sens. 2005, 26, 3763–3779. [Google Scholar] [CrossRef]
- Bunting, P.; Lucas, R.M.; Jones, K.; Bean, A.R. Characterisation and mapping of forest communities by clustering individual tree crowns. Remote Sens. Environ. 2010, 114, 2536–2547. [Google Scholar] [CrossRef]
- Adams, B.T.; Matthews, S.N. Enhancing forest and shrubland mapping in a managed forest landscape with Landsat-LiDAR data fusion. Nat. Areas J. 2018, 38, 402–418. [Google Scholar] [CrossRef]
- Ohmann, J.L.; Gregory, M.J. Predictive mapping of forest composition and structure with direct gradient analysis and nearest-neighbor imputation in coastal Oregon, U.S.A. Can. J. For. Res. 2002, 32, 725–741. [Google Scholar] [CrossRef]
- Thessler, S.; Ruokolainen, K.; Tuomisto, H.; Tomppo, E. Mapping gradual landscape-scale floristic changes in Amazonian primary rain forests by combining ordination and remote sensing. Glob. Ecol. Biogeogr. 2005, 14, 315–325. [Google Scholar] [CrossRef]
- Schmidtlein, S.; Sassin, J. Mapping of continuous floristic gradients in grasslands using hyperspectral imagery. Remote Sens. Environ. 2004, 92, 126–138. [Google Scholar] [CrossRef]
- Gu, H.; Singh, A.; Townsend, P.A. Detection of gradients of forest composition in an urban area using imaging spectroscopy. Remote Sens. Environ. 2015, 167, 168–180. [Google Scholar] [CrossRef]
- Adams, B.T.; Matthews, S.N.; Peters, M.P.; Prasad, A.; Iverson, L.R. Mapping floristic gradients of forest composition using an ordination-regression approach with Landsat OLI and terrain data in the Central Hardwoods region. For. Ecol. Manag. 2019, 434, 87–98. [Google Scholar] [CrossRef]
- Hakkenberg, C.R.; Peet, R.K.; Urban, D.L.; Song, C. Modeling plant composition as community-continua in a forest landscape with LiDAR and hyperspectral remote sensing. Ecol. Appl. 2018, 28, 177–190. [Google Scholar] [CrossRef] [PubMed]
- Feilhauer, H.; Faude, U.; Schmidtlein, S. Combining Isomap ordination and imaging spectroscopy to map continuous floristic gradients in a heterogeneous landscape. Remote Sens. Environ. 2011, 115, 2513–2524. [Google Scholar] [CrossRef]
- Harris, A.; Charnock, R.; Lucas, R.M. Hyperspectral remote sensing of peatland floristic gradients. Remote Sens. Environ. 2015, 162, 99–111. [Google Scholar] [CrossRef] [Green Version]
- Manning, A.D.; Lindenmayer, D.B.; Nix, H.A. Continua and Umwelt: Novel perspectives on viewing landscapes. Oikos 2004, 104, 621–628. [Google Scholar] [CrossRef]
- Schmidtlein, S.; Zimmermann, P.; Schüpferling, R.; Weiß, C. Mapping the floristic continuum: Ordination space position estimated from imaging spectroscopy. J. Veg. Sci. 2007, 18, 131–140. [Google Scholar] [CrossRef]
- Iverson, L.R.; Peters, M.P.; Bartig, J.; Rebbeck, J.; Hutchinson, T.F.; Matthews, S.N.; Stout, S. Spatial modeling and inventories for prioritizing investment into oak-hickory restoration. For. Ecol. Manag. 2018, 424, 355–366. [Google Scholar] [CrossRef]
- Iverson, L.R.; Bartig, J.L.; Nowacki, G.J.; Peters, M.P.; Dyer, J.M.; Hutchinson, T.F.; Matthews, S.N.; Adams, B.T. USDA Forest Service Section, Subsection, and Landtype Descriptions for Southeastern Ohio; Research Map NRS-10 [Printed map included]; Department of Agriculture, Forest Service, Northern Research Station: Newtown Square, PA, USA, 2019; p. 68. [CrossRef]
- Cleland, D.T.; Freeouf, J.A.; Keys, J.E.; Nowacki, G.J.; Carpenter, C.A.; McNab, W.H. Ecological Subsections: Sections and Subsections for the Conterminous United States; Gen. Tech. Report WO-76D [Map on CD-ROM], Sloan, A.M. cartographer, presentation scale 1:3,500,000, colored; Department of Agriculture, Forest Service: Washington, DC, USA, 2007.
- Hix, D.M.; Pearcy, J.N. Forest ecosystems of the Marietta Unit, Wayne National Forest, Southeastern Ohio: Multifactor classification and analysis. Can. J. For. Res. 1997, 27, 1117–1131. [Google Scholar] [CrossRef]
- Stout, W. The charcoal iron industry of the Hanging Rock Iron District—Its influence on the early development of the Ohio Valley. Ohio State Archaeol. Hist. Q. 1933, 42, 72–104. [Google Scholar]
- Iverson, L.R.; Hutchinson, T.F.; Peters, M.P.; Yaussy, D.A. Long-term response of oak-hickory regeneration to partial harvest and repeated fires: Influence of light and moisture. Ecosphere 2017, 8, e01642. [Google Scholar] [CrossRef]
- Palus, J.D.; Goebel, P.C.; Hix, D.M.; Matthews, S.N. Structural and compositional shifts in forests undergoing mesophication in the Wayne National Forest, Southeastern Ohio. For. Ecol. Manag. 2018, 430, 413–420. [Google Scholar] [CrossRef]
- Marquis, D.A.; Ernst, R.L.; Stout, S.L. Prescribing Silvicultural Treatments in Hardwood Stands of the Alleghenies (Revised); Gen. Tech. Rep. NE-96; Department of Agriculture, Forest Service, Northeastern Forest Experimental Station: Broomall, PA, USA, 1992; p. 101.
- Brose, P.H.; Gottschalk, K.W.; Horsley, S.B.; Knopp, P.D.; Kochenderfer, J.N.; McGuinness, B.J.; Miller, G.W.; Ristau, T.E.; Stoleson, S.H.; Stout, S.L. Prescribing Regeneration Treatments for Mixed-Oak Forests in the Mid-Atlantic Region; Gen. Tech. Rep. NRS-33; Department of Agriculture, Forest Service, Northern Research Station: Newtown Square, PA, USA, 2008; p. 100. [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the Fmask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4-7, 8, and Sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Crist, E.P. A TM Tasseled Cap equivalent transformation for reflectance factor data. Remote Sens. Environ. 1985, 17, 301–306. [Google Scholar] [CrossRef]
- Hijmans, R.J.; van Etten, J.; Cheng, J.; Mattiuzzi, M.; Sumner, M.; Greenberg, J.A.; Lamigueiro, O.P.; Bevan, A.; Racine, E.B.; Shortridge, A. Raster: Geographic Data Analysis and Modeling. R Package Version 2.6–7. 2017. Available online: https://cran.r-project.org/package=raster (accessed on 2 June 2017).
- Beers, T.W.; Dress, P.E.; Wensel, L.C. Aspect transformation in site productivity research. J. For. 1966, 64, 691–692. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef] [Green Version]
- De Reu, J.; Bourgeois, J.; Bats, M.; Zwertvaegher, A.; Gelorini, V.; De Smedt, P.; Chu, W.; Antrop, M.; De Maeyer, P.; Finke, P.; et al. Application of the topographic position index to heterogeneous landscapes. Geomorphology 2013, 186, 39–49. [Google Scholar] [CrossRef]
- Ohmann, J.L.; Gregory, M.J.; Roberts, H.M. Scale considerations for integrating forest inventory plot data and satellite image data for regional forest mapping. Remote Sens. Environ. 2014, 151, 3–15. [Google Scholar] [CrossRef]
- Stehman, S.V.; Wickham, J.D. Pixels, blocks of pixels, and polygons: Choosing a spatial unit for thematic accuracy assessment. Remote Sens. Environ. 2011, 115, 3044–3055. [Google Scholar] [CrossRef]
- Iverson, L.R.; Prasad, A.M. Predicting abundance of 80 tree species following climate change in the eastern United States. Ecol. Monogr. 1998, 68, 465–485. [Google Scholar] [CrossRef]
- Dufrêne, M.; Legendre, P. Species assemblages and indicator species: The need for a flexible asymmetrical approach. Ecol. Monogr. 1997, 67, 345–366. [Google Scholar] [CrossRef]
- De’ath, G. Multivariate regression trees: A new technique for modeling species–environment relationships. Ecology 2002, 83, 1105–1117. [Google Scholar] [CrossRef]
- De’ath, G. Mvpart: Multivariate Partitioning, R Package Version 1.6–2; 2014. Available online: https://mran.microsoft.com/snapshot/2014-12-11/web/packages/mvpart/index.html (accessed on 2 June 2017).
- Oksanen, J.; Blanchet, F.G.; Freindly, M.; Kindt, R.; Legendre, P.; McGlinn, D.; Minchin, P.R.; O’Hara, R.B.; Simpson, G.L.; Solymos, P.; et al. Vegan: Community Ecology Package, R Package Version 2.4–6; 2018. Available online: https://cran.r-project.org/package=vegan (accessed on 2 June 2017).
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Jin, S.; Danielson, P.; Homer, C.; Gass, L.; Bender, S.M.; Case, A.; Costello, C.; Dewitz, J.; Fry, J.; et al. A new generation of the United States National Land Cover Database: Requirements, research priorities, design, and implementation strategies. ISPRS J. Photogramm. Remote Sens. 2018, 146, 108–123. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef] [Green Version]
- Carvell, K.; Tryon, E. The effect of environmental factors on the abundance of oak regeneration beneath mature oak stands. For. Sci. 1961, 7, 98–105. [Google Scholar] [CrossRef]
- Nowacki, G.J.; Abrams, M.D. The demise of fire and “mesophication” of forests in the eastern United States. Bioscience 2008, 58, 123–138. [Google Scholar] [CrossRef]
- Shifley, S.R.; Moser, W.K. Future Forests of the Northern United States; Gen. Tech. Rep. NRS-151; Department of Agriculture, Forest Service, Northern Research Station: Newtown Square, PA, USA, 2016; p. 388. [CrossRef] [Green Version]
- King, D.I.; Schlossberg, S. Synthesis of the conservation value of the early-successional stage in forests of eastern North America. For. Ecol. Manag. 2014, 324, 186–195. [Google Scholar] [CrossRef]
- Feilhauer, H.; Schmidtlein, S. Mapping continuous fields of forest alpha and beta diversity. Appl. Veg. Sci. 2009, 12, 429–439. [Google Scholar] [CrossRef]
- Thompson, S.D.; Nelson, T.A.; White, J.C.; Wulder, M.A. Mapping dominant tree species over large forested areas using Landsat best-available-pixel image composites. Can. J. Remote Sens. 2015, 41, 203–218. [Google Scholar] [CrossRef]
- Melaas, E.K.; Sulla-Menashe, D.; Gray, J.M.; Black, T.A.; Morin, T.H.; Richardson, A.D.; Friedl, M.A. Multisite analysis of land surface phenology in North American temperate and boreal deciduous forests from Landsat. Remote Sens. Environ. 2016, 186, 452–464. [Google Scholar] [CrossRef]
- Melaas, E.K.; Friedl, M.A.; Zhu, Z. Detecting interannual variation in deciduous broadleaf forest phenology using Landsat TM/ETM+ data. Remote Sens. Environ. 2013, 132, 176–185. [Google Scholar] [CrossRef]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.-C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Janowiak, M.K.; Iverson, L.R.; Fosgitt, J.; Handler, S.D.; Dallman, M.; Thomasma, S.; Hutnik, B.; Swanston, C.W. Assessing stand-level climate change risk using forest inventory data and species distribution models. J. For. 2017, 115, 222–229. [Google Scholar] [CrossRef]
- Gómez, C.; White, J.C.; Wulder, M.A. Optical remotely sensed time series data for land cover classification: A review. ISPRS J. Photogramm. Remote Sens. 2016, 116, 55–72. [Google Scholar] [CrossRef] [Green Version]










| Landsat 8-OLI (P 18-19/R 32-33; 330 Images) | Date Range (Years)/Abbv. | |
|---|---|---|
| Seasonal composites (Bands 1–7) | ||
| Leaf-on (Summer) | 1 June–30 August (2014–2017) | |
| Transition (Fall) | 15 September–15 November (2014–2017) | |
| Leaf-off (Winter) | 1 December–28 February (2014–2018) | |
| Transition (Spring) | 1 April–1 May (2014–2017) | |
| Seasonal TCT/Spectral indices composites [51] | ||
| Tasseled Cap Brightness | TCB | |
| Tasseled Cap Greenness | TCG | |
| Tasseled Cap Wetness | TCW | |
| Enhanced Vegetation Index | EVI | |
| Harmonic metrics (2nd order Fourier series coefficients) | ||
| Mean (intercept) | INT | |
| Trend (slope) | TRE | |
| Cosine terms 1-2 | CO1, CO2 | |
| Sine terms 1-2 | SI1, SI2 | |
| RMSE | RMS | |
| Topographic variables | ||
| DEM: Elevation (30 m) | ELE | |
| Slope [52] | SLO | |
| Transformed aspect: Eastingness [53] | EAS | |
| Transformed aspect: Northingness [53] | NOR | |
| Topographic Wetness Index [54] | TWI | |
| Topographic Position Index [55] | TPI | |
| Deviation from mean elevation [55] | DEV | |
| Class Name | Abbv. | Diagnostic Species | Sample Size |
|---|---|---|---|
| Early-successional | ES | … | 352 |
| Pine plantations/Mixed pine | PP | Cercis canadensis, Pinus resinosa, Pinus rigida, Pinus strobus, Populus grandidentata | 340 |
| Floodplain hardwoods/Bottomlands hydric | BH | Aesculus flava, Betula nigra, Fraxinus americana, Juglans nigra, Platanus occidentalis, Ulmus americana | 285 |
| Bottomlands mixed hardwoods | BM | Fagus grandifolia, Liriodendron tulipifera | 311 |
| Dry-mesic mixed mesophytic hardwoods | DM | Carya spp. | 202 |
| Upland mesophytic hardwoods | UM | Acer saccharum, Tilia americana, Quercus rubra | 540 |
| Dry-oak dominated hardwoods | DO | Quercus alba, Quercus coccinea, Quercus montana, Quercus velutina | 580 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adams, B.; Iverson, L.; Matthews, S.; Peters, M.; Prasad, A.; Hix, D.M. Mapping Forest Composition with Landsat Time Series: An Evaluation of Seasonal Composites and Harmonic Regression. Remote Sens. 2020, 12, 610. https://doi.org/10.3390/rs12040610
Adams B, Iverson L, Matthews S, Peters M, Prasad A, Hix DM. Mapping Forest Composition with Landsat Time Series: An Evaluation of Seasonal Composites and Harmonic Regression. Remote Sensing. 2020; 12(4):610. https://doi.org/10.3390/rs12040610
Chicago/Turabian StyleAdams, Bryce, Louis Iverson, Stephen Matthews, Matthew Peters, Anantha Prasad, and David M. Hix. 2020. "Mapping Forest Composition with Landsat Time Series: An Evaluation of Seasonal Composites and Harmonic Regression" Remote Sensing 12, no. 4: 610. https://doi.org/10.3390/rs12040610
APA StyleAdams, B., Iverson, L., Matthews, S., Peters, M., Prasad, A., & Hix, D. M. (2020). Mapping Forest Composition with Landsat Time Series: An Evaluation of Seasonal Composites and Harmonic Regression. Remote Sensing, 12(4), 610. https://doi.org/10.3390/rs12040610