Climate variability and human interventions are commonly considered two major contributors to variations in inland lakes [
25]. To identify lake disturbances that are dominated by different factors using time series remote sensing data, this paper proposes a lake disturbance identification algorithm that consists of two parts: the first is the Douglas-Peucker algorithm [
26] and the bend simplification algorithm [
27] to segment the time series of Landsat data derived lake surface areas. Second, according to the documented lake surface area change records, the features of the major lake surface area disturbances are summarized and extracted based the time series of lake surface area and to identify the major lake surface area disturbances. The specific steps are as follows: (1) building time series with lake surface areas; (2) curve simplification following the Douglas-Peucker algorithm; (3) bend simplification to further simplify the segmented time series curve; (4) feature extraction and event identification.
3.1. Lake Surface Extraction and Building Time Series with Lake Surface Areas
Many methods have been proposed to identify inland water surfaces since the emergence of remote sensing technology. Widely used water indices include the NDWI, modified normalized difference water index (MNDWI), enhanced water index (EWI), automated water extraction index (AWEI), multiband water index (MBWI) and WI2015 [
28]. However, among these methods, the water index-based method has proven to be simple and effective for extracting the water body [
29,
30,
31]. Therefore, in this study, we adopted the MNDWI index combined with the Otsu algorithm to adaptively determine the optimum segmentation threshold for extracting lake areas from the Landsat images. The Otsu method, proposed by Otsu [
32], is a self-adaptive thresholding method that is also referred to as the maximum interclass variance method derived by least square estimation. The Otsu method was used in this study to exclude the influence of mis-segmentation between water and non-water areas caused by artificially set thresholds to the MNDWI.
The MNDWI that was obtained by Xu [
33] by revising the waveband combination of the NDWI is one of the most typical and most widely used methods for water extraction. The basic principle of this index is that the reflectivity of water in the mid-infrared band continues to decrease, while the reflectivity of ground features, such as soil and buildings, abruptly increases from the near-infrared band to the mid-infrared band. This pattern greatly reduces confusing water and buildings, reduces the background noise and benefits the extraction of water surface. Therefore, in this study, we use the MNDWI (see Equation (1)) to extract water bodies, as follows:
where Green represents the green light band and MIR is the mid-infrared band.
The single-band threshold method was used to extract water from the HJ-1A/1B images. After PC (principal component) transformation of the HJ-1A/1B data, a significant difference between water and non-water was maximized on the second component (or band) [
34]. Thus, by selecting an appropriate threshold, water information can be satisfactorily extracted using the single-band method.
Analysis of a time series curve plotted with sufficiently continuous lake area data not only effectively reflects the lake area variation trend but also captures any major lake disturbance events. In this study, the input data used to construct the time series curve were the annual average lake area measurements extracted from the remote sensing images during each dry season (November to April of the next year) from 1987 to 2017.
3.2. Time Series Lake Surface Area Curve Segmentation and Identification of Disturbance Events
(1) Simplification of the time series curve using the Douglas-Peucker algorithm
The occurrence of large natural or human activities in (or around) a lake will cause lake area disturbances. For example, dam construction or water storage in a lake will cause a sudden increase in lake area, whereas land reclamation around a lake will cause a rapid decrease in lake area. Furthermore, strong natural events such as rainfall or drought can also cause increases or decreases in lake area. Such event-induced lake changes manifest as sudden changes in the time series lake surface area curve. However, minor events or precipitation differences will also cause variations in the time series curve. These changes are not key factors affecting the lake area but may be obstacles to the identification of key disturbances; thus, they are considered noise that should be removed for the time-series analysis.
Several methods, such as LandTrendr [
35], CCDC [
36] and BFAST [
37], have been proposed to identify disturbances using remotely sensed time series indices (such as NDVI (Normalized Difference Vegetation Index), NBR (Normalized Burn Ratio), TCA (Tasselled Cap Angle). However, most of the lake surface area time series appear to be purely random and nonstationary time series (see
Table 2); unlike indices such as NDVI, NBR and TCA, lake surface areas are limitless (there is theoretically no upper boundaries for lake areas), which means existing models, such as LandTrendr, CCDC, and BFAST, are theoretically unsuitable (or could not be directly used) for the analysis of lake surface area time series. Fortunately, the Douglas-Peucker (D-P) line simplification algorithm, which is used to eliminate low-intensity noises and smooth minor changes on the curve to better capture larger changes on the curve, is an appropriate alternative.
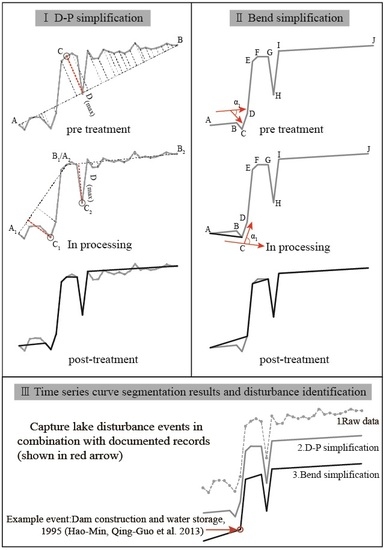
The D-P algorithm was proposed by Douglas and Peucker in 1973 [
26]. Currently, this algorithm is recognized as a classical algorithm for vector line simplification in GIS (geographic informational system). The basic idea of the algorithm is as follows: (1) line AB (see
Figure 2) connects the two end points A and B of a time series curve, forming the chord of the curve; (2) for each of the points (for example, point C) between A and B on the curve, there will be a distance to this chord (to line AB), forming a set of distances D, and the maximum distance of D is d(max); (3) d(max) is then compared with the given tolerance ε, and if d(max) is smaller than ε, then line AB is taken to be the approximation of the curve, and the processing of this curve section ends, but if d(max) is larger than ε, then the corresponding point (point C) is used to divide the curve into two subsegments (AC and BC), and each of the two subsegments is further processed following steps 1 through 3 until each of their d(max) values is less than the given ε; (4) after all the curves are processed, the segmentation points are connected sequentially to form a polyline that represents a simplification of the curve.
(2) Bend simplification and time series curve segmentation
After D-P simplification of the time series curve, several minor-change points may not have been removed. As these points are not indicative of major lake disturbances, they should be removed. To retain only the feature points with the main fluctuations on time series curves, we used the bend simplification algorithm, which can eliminate smaller fluctuations [
38], to simplify the D-P algorithm simplified curve.
The bend simplification algorithm was used to determine whether the variation in the curvature at each point is smooth. Given a predefined threshold, if the curvature was smaller than the threshold, the point was eliminated and a new segment was created between the two points adjacent to the eliminated point. However, if the curvature exceeded the predefined threshold, the corresponding point was considered a potential feature point and was retained. After each point was processed, the retained potential points were then connected sequentially to form the finally simplified time series curve. The specific steps of the bend simplification algorithm are illustrated in
Figure 2 and are explained as follows: (1) first, we calculated the curvatures on each point of the curve except for the first and last points; (2) second, for the curvature on the second point (for example point B), the two adjacent points A and C were used to construct vectors AB and BC, and the angle formed by these two vectors was calculated as α1; if α1 was larger than the preset threshold α, the curvature on point B was considered to be large and was retained as a key point; however, if the angle α1 between vector AB and BC was less than the preset threshold α, point B was removed. Following the steps above, curvatures on point C, D, etc. were judged one by one; (3) after step (2), all points, except the beginning and the end points, that meet the given curvature threshold α were retained as feature points that are representative of the main lake surface area change events.
(3) Feature extraction and disturbance identification
By setting appropriate segmentation parameters, disturbances that were considered “major” by users were obtained. For the segmented time series, each segment represents different lake disturbance events. When the lake was greatly disturbed by major influences, the variation in the time series curve was distinguishable. According to the segmented curves, lake surface disturbance features such as the trajectory, duration and recovery rate were extracted to classify each disturbance following an unsupervised clustering method. For these extracted features, the trajectory here was defined as the curve that formed by lake surface areas changing with time. To quantify disturbances within each trajectory, we defined two indicators: disturbance duration and disturbance recovery rate. For each disturbance, there were beginning and ending points, the time-span between these two points was defined as disturbance duration (if not, disturbance duration was defined as infinity). For each disturbance, there will be a rate; the disturbance event rate was defined as the area difference between the beginning and the end of a segment divided by the disturbance duration (see Equations (2) and (3)). For each disturbance, there were two adjacent segments. The recovery rate was the area change ratio between prior segment and the next (see Equations (4) and (5)). Features we used for disturbance classification are as follows:
Feature recovery rate:
where
represents the lake area at point a and
is the time (year) of disturbance at point a;
denotes lake surface area difference between point a and point b;
is disturbance recovery rate for disturbance at point b, details are as illustrated in
Figure 3.
Unlike trajectory classifications of disturbances in forests, lake disturbance classifications are small sample-based classification tasks, because major lake surface area disturbances are small probability events that cause training sample insufficiency of classifiers, such as statistical classifiers, machine learning classifiers or artificial intelligence classifiers. Therefore, we used the k-means clustering [
39] method to classify disturbances into anthropogenic or natural events.
(4) Lake surface area disturbance identification accuracy assessment
Disturbance identification accuracy was determined using the confusion matrix, which uses overall accuracy (OA) to represent the percentage of correctly classified disturbances, the user’s accuracy (UA) to denote how well training-set samples are classified, and the producer’s accuracy (PA) to show the probability that a classified sample represents a given class in reality [
40]. In this study, we used
and
to represent the user’s accuracies of anthropogenic disturbances and natural disturbances and the
and
to represent the producer’s accuracies of anthropogenic disturbances and natural disturbances (see
Table 3). We employed the method given by Adeline et al. [
41] to evaluate the disturbances identification accuracy levels, and validation samples were randomly selected from the documented disturbance event records. Reference data and predicted results of the confusion matrix were defined as TP (true positive), TN (true negative), FP (false positive) and FN (false negative). TP denotes the number of correctly classified as anthropogenic disturbances, TN is the number of correctly detected as natural disturbances, FP represents the number of natural disturbances misclassified as anthropogenic disturbances and FN is the number of anthropogenic disturbances misclassified as natural disturbances. As the F-score strikes a good balance between under- and over-detection accuracy levels, it was used in this study to evaluate the accuracy of the methods used (see
Table 3).