Radiometric Cross Calibration and Validation Using 4 Angle BRDF Model between Landsat 8 and Sentinel 2A
Abstract
:1. Introduction
- Simultaneous image pairs acquired at two Saharan desert locations during a two- day underfly event on March 29–30, 2013. One location was near the Libya4 PICS (WRS2 path 182, rows 42–43); the other was over the WRS2 path 198 rows 38–39.
- Time series analysis of images acquired over the Libya4 PICS
1.1. Satellite/Sensor Comparison
1.2. Spectral Response
2. Methodology
- Data Preprocessing and Site Selection
- Spectral Band Adjustment Factor (SBAF) Correction
- Bidirectional Reflectance Distribution Factor Normalization
- Gain and Offset Estimation
2.1. Data Preprocessing and Site Selection
2.2. Spectral Band Adjustment Factor (SBAF) Correction
| =in-band TOA reflectance of OLI (Unitless) | |
| =in-band TOA reflectance of MSI (Unitless) | |
| =hyperspectral TOA reflectance profile of the target (Unitless) | |
| =OLI relative spectral response | |
| =MSI relative spectral response |
2.3. BRDF Modeling and Normalization
2.4. Gain and Offset Calculation
2.5. Uncertainty Analysis
2.5.1. Uncertainty Due to Sensor Calibration
2.5.2. Uncertainty Due to Changes in Prelaunch RSR
2.5.3. Uncertainty Due to Site Nonuniformity
2.5.4. Uncertainty due to Solar Position (Overpass Time Differences)
2.5.5. Uncertainty due to Atmospheric Effects
2.5.6. Summary of Uncertainty Analysis
3. Validation
- There was insufficient evidence to indicate differences between OLI and MSI mean TOA reflectances in the coastal aerosol, red, and SWIR2 bands when either set of gains was applied. The offsets were not statistically significant, and the gains were essentially equal.
- There was sufficient evidence to indicate differences between OLI and MSI mean TOA reflectances in the NIR band. Using the gain with offset, the difference was less statistically significant, perhaps not surprising given the observed outliers in the OLI reflectances.
- There was sufficient evidence to indicate differences in the green band.
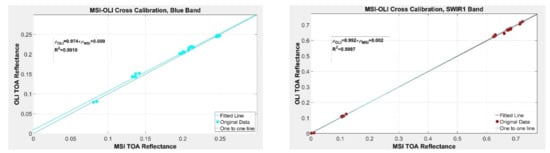
- Both tests found sufficient evidence to indicate differences in TOA reflectance in the blue band when gain with offset was applied. This is likely due to the apparent non-normality observed in the OLI reflectances. The disagreement with the Wilcoxon test results when gain only was considered should be expected, as the cross-calibration offset was found to be significant in this band.
- Both tests found insufficient evidence to indicate differences in reflectance in the SWIR1 band when gain with offset was considered but sufficient evidence to indicate differences when gain only was considered. However, the strength of evidence in the gain-only case was very “weak”, as the p-value was close to 0.05. This may be due to the fact that the variance in MSI reflectance was slightly larger than the corresponding OLI reflectance variance, which would violate the assumption of equal variance required in the two-sample t test.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Helder, D.L.; Markham, B.L.; Thome, K.J.; Barsi, J.A.; Chander, G.; Malla, R. Updated Radiometric Calibration for the Landsat-5 Thematic Mapper Reflective Bands. IEEE Trans. Geosci. Remote Sens. 2008, 10, 3309–3325. [Google Scholar] [CrossRef]
- Markham, B.L.; Helder, D.L. Forty-year calibrated record of earth-reflected radiance from Landsat: A review. Remote Sens. Environ. 2012, 122, 30–40. [Google Scholar] [CrossRef] [Green Version]
- Helder, D.L.; Basnet, B.; Morstad, D. Optimized identification of worldwide radiometric pseudo-invariant calibration sites. Can. J. Remote Sens. 2010, 36, 527–539. [Google Scholar] [CrossRef]
- Nagaraja Rao, C.R.; Chen, J. Inter-satellite calibration linkages for the visible and near-infared channels of the Advanced Very High Resolution Radiometer on the NOAA-7,-9, and-11 spacecraft. Int. J. Remote Sens. 1995, 16, 1931–1942. [Google Scholar] [CrossRef]
- Cosnefroy, H.; Leroy, M.; Briottet, X. Selection and characterization of Saharan and Arabian desert sites for the calibration of optical satellite sensors. Remote Sens. Environ. 1996, 58, 101–114. [Google Scholar] [CrossRef]
- Chander, G.; Angal, A.; Helder, D.L.; Mishra, N.; Wu, A. Preliminary assessment of several parameters to measure and compare usefulness of the CEOS reference pseudo-invariant calibration sites. Remote Sens. 2010, 7826, 78262L. [Google Scholar]
- Morstad, D.L.; Helder, D.L. Use of Pseudo-Invariant Sites for Long-Term Sensor Calibration. Int. Geosci. Remote Sens. Symp. (IGARSS) 2008, 1, I-253–I-256. [Google Scholar] [CrossRef]
- Hasan, M.N.; Shrestha, M.; Leigh, L.; Helder, D. Evaluation of an Extended PICS (EPICS) for Calibration and Stability Monitoring of Optical Satellite Sensors. Remote Sens. 2019, 11, 1755. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, M.; Leigh, L.; Helder, D. Classification of North Africa for Use as an Extended Pseudo Invariant Calibration Sites (EPICS) for Radiometric Calibration and Stability Monitoring of Optical Satellite Sensors. Remote Sens. 2019, 11, 875. [Google Scholar] [CrossRef] [Green Version]
- Philippe Teillet, M.; Fedosejevs, G.; Thome, K.J. Spectral band difference effects on radiometric cross-calibration between multiple satellite sensors in the Landsat solar-reflective spectral domain. In Sensors, Systems, and Next-Generation Satellites; International Society for Optics and Photonics: Bellingham, WA, USA, 2004. [Google Scholar] [CrossRef]
- Chander, G.; Mishra, N.; Helder, D.; Aaron, D.; Choi, T.; Angal, A.; Xiong, X. Use of EO-1 Hyperion data to calculate spectral band adjustment factors (SBAF) between the L7 ETM+ and Terra MODIS sensors. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 1667–1670. [Google Scholar] [CrossRef]
- Chander, G.; Mishra, N.; Helder, D.L.; Aaron, D.B.; Angal, A.; Choi, T.; Xiong, X.; David Doelling, R. Applications of Spectral Band Adjustment Factors(SBAF) for Cross-Calibration. Geosci. Remote Sens. IEEE Trans. 2013, 51, 1267–1281. [Google Scholar] [CrossRef]
- Liu, J.J.; Li, Z.; Qiao, Y.L.; Liu, Y.J.; Zhang, Y.X. A new method for cross-calibration of two satellite sensors. Int. J. Remote Sens. 2004, 25, 5267–5281. [Google Scholar] [CrossRef]
- Roujean, J.L.; Leroy, M.; Deschamps, P.Y. A bi-directional reflectance model of the Earth’s surface for the correction of remote sensing data. J. Geophys. Res. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Schlapfer, D.; Richter, R.; Feingersh, T. Operational BRDF Effects Correction for Wide-Field-of-View Optical Scanners (BREFCOR). IEEE Trans. Geosci. Remote Sens. 2015, 53, 1855–1864. [Google Scholar] [CrossRef] [Green Version]
- Mishra, N.; Helder, D.; Angal, A.; Choi, J.; Xiong, X. Absolute Calibration of Optical Satellite Sensors Using Libya 4 Pseudo Invariant Calibration Site. Remote Sens. 2014, 6, 1327–1346. [Google Scholar] [CrossRef] [Green Version]
- Lacherade, S.; Fougnie, B.; Henry, P.; Gamet, P. Cross Calibration Over Desert Sites: Description, Methodology, and Operational Implementation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1098–1113. [Google Scholar] [CrossRef]
- Mishra, N.; Haque, M.O.; Leigh, L.; Aaron, D.; Helder, D.; Markham, B. Radiometric Cross Calibration of Landsat 8 Operational Land Imager (OLI) and Landsat 7 Enhanced Thematic Mapper Plus (ETM+). Remote Sens. 2014, 6, 12619–12638. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Ganguly, S.; Dungan, J.L.; Wang, W.L.; Nemani, R.R. Sentinel-2 MSI Radiometric Characterization and Cross-Calibration with Landsat-8 OLI. Adv. Remote Sens. 2017, 6, 147–159. [Google Scholar] [CrossRef] [Green Version]
- Pinto, C.T.; Ponzoni, F.J.; Castro, R.M.; Leigh, L.; Kaewmanee, M.; Aaron, D.; Helder, D. Evaluation of the uncertainty in the spectral band adjustment factor (SBAF) for cross-calibration using Monte Carlo simulation. Remote Sens. Lett. 2016, 7, 837–846. [Google Scholar] [CrossRef]
- Chander, G.; Helder, D.L.; Aaron, D.; Mishra, N.; Shrestha, A.K. Assessment of Spectral, Misregistration, and Spatial Uncertainties Inherent in the Cross-Calibration Study. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1282–1296. [Google Scholar] [CrossRef]
- Gorroño, J.; Banks, A.C.; Fox, N.P.; Underwood, C. Radiometric inter-sensor cross-calibration uncertainty using a traceable high accuracy reference hyperspectral imager. ISPRS J. Photogramm. Remote Sens. 2013, 130, 393–417. [Google Scholar] [CrossRef] [Green Version]
- The Worldwide Reference System. Available online: https://landsat.gsfc.nasa.gov/the-worldwide-reference-system (accessed on 8 November 2017).
- Gascon, F.; Bouzinac, C.; Thépaut, O.; Jung, M.; Francesconi, B.; Louis, J.; Lonjou, V.; Lafrance, B.; Massera, S.; Gaudel-Vacaresse, A.; et al. Copernicus Sentinel-2A Calibration and Products Validation Status. Remote Sens. 2017, 9, 584. [Google Scholar] [CrossRef] [Green Version]
- Sentinel 2 Handbook. Available online: https://sentinel.esa.int/documents/247904/685211/Sentinel-2/User/Handbook (accessed on 8 November 2017).
- Sentinel 2 Technical guide. Available online: https://earth.esa.int/web/technical-guides/sentinel-2-msi/performance (accessed on 8 November 2017).
- Barsi, J.A.; Lee, K.; Kvaran, G.; Markham, B.L.; Jeffrey Pedelty, A. The Spectral Response of the Landsat-8 Operational Land Imager. Remote Sens. 2014, 6, 10232–10251. [Google Scholar] [CrossRef] [Green Version]
- Harika, V. Normalization of Pseudo-invariant Calibration Sites for Increasing the Temporal Resolution and Long-Term Trending. Master’s Thesis, South Dakota State University, Brookings, SD, USA, 2017. Available online: https://openprairie.sdstate.edu/etd/2180/ (accessed on 21 September 2018).
- Farhad, M.M. Cross Calibration and Validation of Landsat 8 OLI and Sentinel 2A MSI. Master’s Thesis, Department of Electrical Engineering, South Dakota State University, Brookings, SD, USA, 2018. [Google Scholar]
- Sentinel 2 Data Quality Reports. 8 February 2018. Available online: https://sentinel.esa.int/documents/247904/685211/Sentinel-2-Data-Quality-Report (accessed on 28 February 2018).
- Brian Markham. Available online: https://landsat.usgs.gov/sites/default/files/documents/landsat_science_team/2018-02_Day1_Markham_Landsat%20Calibration%20and%20Validation.pdf (accessed on 21 September 2018).
- Sentinel 2 Technical guide and performance. Available online: https://earth.esa.int/web/sentinel/technical-guides/sentinel-2-msi/performance (accessed on 21 September 2018).
- Sentinel2 processing baselines. Available online: https://sentinel.esa.int/web/sentinel/missions/sentinel-2/news/-/article/new-processing-baseline-02-04-for-sentinel-2a-products (accessed on 7 March 2018).







| Target Site | WRS2 Path | WRS2 Row | Center Lattitude | Center Longitude | Site Length | Site Width |
|---|---|---|---|---|---|---|
| Libya1 | 187 | 43 | 24.71 | 13.49 | 33,990 m | 34,920 m |
| Libya4 | 181 | 40 | 28.55 | 23.38 | 21,690 m | 19,980 m |
| Niger2 | 188 | 45 | 21.36 | 10.55 | 25,320 m | 33,480 m |
| Sudan1 | 177 | 45 | 21.58 | 27.70 | 38,400 m | 22,680 m |
| Lake Tahoe | 43 | 33 | 39.09 | −120.03 | 11,220 m | 11,190 m |
| Volcanic Near Libya | 184 | 43 | 24.86 | 23.77 | 5962 m | 9118 m |
| Band | CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 |
|---|---|---|---|---|---|---|---|
| SBAF | 1.0015 | 0.9594 | 1.0066 | 0.9790 | 0.9996 | 0.9988 | 0.9989 |
| Standard Daviation | 0.0001 | 0.0027 | 0.0013 | 0.0010 | 0.0050 | 0.0030 | 0.0070 |
| Site | Hyperion Scenes Used | Bands | ||||||
|---|---|---|---|---|---|---|---|---|
| CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 | ||
| Libya 1 | 81 | 1.0017 | 0.9603 | 1.0217 | 0.9777 | 0.9990 | 0.9988 | 1.0010 |
| Niger 2 | 12 | 1.0016 | 0.9681 | 1.0112 | 0.9794 | 1.0003 | 0.9989 | 1.0002 |
| Sudan 1 | 152 | 1.0015 | 0.9643 | 1.0131 | 0.9793 | 1.0001 | 0.9991 | 1.0003 |
| Lake Tahoe | 25 | 1.0201 | 1.0801 | 0.9820 | 1.0180 | 1.0050 | 0.9980 | 0.9980 |
| Volcanic near Libya | 4 | 1.0015 | 0.9659 | 1.0058 | 0.9800 | 1.0001 | 0.9990 | 0.9981 |
| Bands | Before Correction | Normalization with Linear SZA based Model (Spherical Coordinate) | Normalization with Quadratic SZA based Model (Spherical Coordinate) | Normalization with Multi-linear 4 Angle BRDF Model (Plane Cartesian Coordinate) | Normalization with Quadratic Multi-linear 4-angle BRDF Model with Interactions (Plane Cartesian Coordinate) |
|---|---|---|---|---|---|
| CA | 1.5 | 1.19 | 1.08 | 1.19 | 0.98 |
| Blue | 1.25 | 1.19 | 1.12 | 1.15 | 0.85 |
| Green | 1.08 | 0.93 | 0.93 | 0.89 | 0.78 |
| Red | 1.23 | 0.85 | 0.84 | 0.81 | 0.74 |
| NIR | 1.28 | 0.73 | 0.69 | 0.65 | 0.65 |
| SWIR1 | 2.08 | 0.61 | 0.60 | 0.58 | 0.53 |
| SWIR2 | 2.48 | 1.91 | 1.80 | 1.76 | 1.52 |
| Site | WRS2 Path/Row | Number of Scene Pairs | Coincident/Near Coincident |
|---|---|---|---|
| Libya 1 | 187/043 | 4 | Coincident |
| Libya 4 | 181/040 | 8 | Coincident |
| Niger 2 | 188/045 | 7 | Coincident |
| Sudan 1 | 177/045 | 9 | Coincident |
| Lake Tahoe | 043/033 | 2 | Coincident |
| Libya Volcano | 184/043 | 5 | Near Coincident |
| Bands | Coefficient | Estimate | Standard Error | t-Stat | p-Value | Null Hypothesis |
|---|---|---|---|---|---|---|
| CA | Bias | 0.0002 | 0.0065 | 0.024 | 0.981 | Failed to Reject |
| Gain | 1.0012 | 0.0326 | 30.668 | Reject | ||
| Blue | Bias | 0.0092 | 0.0035 | 2.605 | 0.0145 | Reject |
| Gain | 0.9741 | 0.0176 | 55.384 | Reject | ||
| Green | Bias | 0.0011 | 0.0020 | 0.509 | 0.6147 | Fail to Reject |
| Gain | 1.0046 | 0.0075 | 133.598 | Reject | ||
| Red | Bias | 0.0031 | 0.0019 | 1.621 | 0.1161 | Fail to Reject |
| Gain | 0.9856 | 0.0048 | 206.628 | Reject | ||
| NIR | Bias | 0.0016 | 0.0015 | 1.031 | 0.311 | Fail to Reject |
| Gain | 0.9923 | 0.0031 | 315.917 | Reject | ||
| SWIR1 | Bias | 0.0018 | 0.0019 | 0.962 | 0.3442 | Fail to Reject |
| Gain | 0.9922 | 0.0031 | 315.498 | Reject | ||
| SWIR 2 | Bias | 0.0011 | 0.0017 | 0.635 | 0.5301 | Fail to Reject |
| Gain | 1.0051 | 0.0034 | 297.390 | Reject |
| Bands | Estimate of Gain | SE | t-Stat | p-Value | Null Hypothesis |
|---|---|---|---|---|---|
| CA | 1.0020 | 0.0052 | 193.63 | Reject | |
| Blue | 1.0186 | 0.0044 | 231.05 | Reject | |
| Green | 1.0083 | 0.0024 | 415.29 | Reject | |
| Red | 0.9928 | 0.0019 | 528.78 | Reject | |
| NIR | 0.9952 | 0.0013 | 770.69 | Reject | |
| SWIR1 | 0.9949 | 0.0013 | 741.21 | Reject | |
| SWIR2 | 1.0070 | 0.0014 | 711.25 | Reject |
| Band | Libya4 | Libya1 | Niger2 | Sudan1 |
|---|---|---|---|---|
| CA | 1.56 | 1.77 | 0.86 | 0.96 |
| Blue | 1.35 | 1.75 | 1.13 | 1.23 |
| Green | 1.80 | 1.79 | 1.30 | 1.22 |
| Red | 1.36 | 1.25 | 1.43 | 1.29 |
| NIR | 1.54 | 1.26 | 1.39 | 1.26 |
| SWIR1 | 1.35 | 1.26 | 0.95 | 0.88 |
| SWIR2 | 1.32 | 1.07 | 1.07 | 1.01 |
| Domain | Source of Uncertainty | Uncertainty (%) |
|---|---|---|
| Spectral | Measured RSR | 1.000 |
| Spectral Filter shift | 0.820 | |
| Spectral Bandwidth Change | 0.280 | |
| Spatial | Registration Error | 0.026 |
| Spatial resolution Mismatch | 0.002 | |
| Site | 1.800 | |
| Temporal | Overpass Time Difference | 2.270 |
| Atmospheric Variation | 1.290 | |
| Sensor | MSI Calibration | 5.000 |
| OLI Calibration | 3.000 | |
| Total Uncertainty | 6.768 | |
| Bands | Set of Gain | Wilcoxon Rank Sum Test | |
|---|---|---|---|
| Null Hypothesis | p-Value | ||
| CA | Gain | Failed to Reject | 0.2846 |
| Gain and Bias | Failed to Reject | 0.2529 | |
| Blue | Gain | Reject | 0.0030 |
| Gain and Bias | Failed to Reject | 0.1410 | |
| Green | Gain | Failed to Reject | 0.0933 |
| Gain and Bias | Failed to Reject | 0.1007 | |
| Red | Gain | Failed to Reject | 0.4076 |
| Gain and Bias | Failed to Reject | 0.8719 | |
| NIR | Gain | Reject | 0.0015 |
| Gain and Bias | Reject | 0.0080 | |
| SWIR1 | Gain | Reject | 0.0312 |
| Gain and Bias | Failed to Reject | 0.1007 | |
| SWIR2 | Gain | Failed to Reject | 0.0877 |
| Gain and Bias | Failed to Reject | 0.1069 | |
| Bands | CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 |
|---|---|---|---|---|---|---|---|
| Gain | 1.0012 | 0.9740 | 1.0046 | 0.9856 | 0.9923 | 0.9922 | 1.0051 |
| Offset | 0.0002 | 0.0092 | 0.0010 | 0.0030 | 0.0016 | 0.0018 | 0.0011 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farhad, M.M.; Kaewmanee, M.; Leigh, L.; Helder, D. Radiometric Cross Calibration and Validation Using 4 Angle BRDF Model between Landsat 8 and Sentinel 2A. Remote Sens. 2020, 12, 806. https://doi.org/10.3390/rs12050806
Farhad MM, Kaewmanee M, Leigh L, Helder D. Radiometric Cross Calibration and Validation Using 4 Angle BRDF Model between Landsat 8 and Sentinel 2A. Remote Sensing. 2020; 12(5):806. https://doi.org/10.3390/rs12050806
Chicago/Turabian StyleFarhad, M M, Morakot Kaewmanee, Larry Leigh, and Dennis Helder. 2020. "Radiometric Cross Calibration and Validation Using 4 Angle BRDF Model between Landsat 8 and Sentinel 2A" Remote Sensing 12, no. 5: 806. https://doi.org/10.3390/rs12050806
APA StyleFarhad, M. M., Kaewmanee, M., Leigh, L., & Helder, D. (2020). Radiometric Cross Calibration and Validation Using 4 Angle BRDF Model between Landsat 8 and Sentinel 2A. Remote Sensing, 12(5), 806. https://doi.org/10.3390/rs12050806