Predicting Wheat Yield at the Field Scale by Combining High-Resolution Sentinel-2 Satellite Imagery and Crop Modelling

Abstract

Accurate prediction of crop yield at the field scale is critical to addressing crop production challenges and reducing the impacts of climate variability and change. Recently released Sentinel-2 (S2) satellite data with a return cycle of five days and a high resolution at 13 spectral bands allows close observation of crop phenology and crop physiological attributes at field scale during crop growth. Here, we test the potential for indices derived from S2 data to estimate dryland wheat yields at the field scale and the potential for enhanced predictability by incorporating a modelled crop water stress index (SI). Observations from 103 study fields over the 2016 and 2017 cropping seasons across Northeastern Australia were used. Vegetation indices derived from S2 showed moderately high accuracy in yield prediction and explained over 70% of the yield variability. Specifically, the red edge chlorophyll index (CI; chlorophyll) (R² = 0.76, RMSE = 0.88 t/ha) and the optimized soil-adjusted vegetation index (OSAVI; structural) (R² = 0.74, RMSE = 0.91 t/ha) showed the best correlation with field yields. Furthermore, combining the crop model-derived SI with both structural and chlorophyll indices significantly enhanced predictability. The best model with combined OSAVI, CI and SI generated a much higher correlation, with R² = 0.91 and RMSE = 0.54 t/ha. When validating the models on an independent set of fields, this model also showed high correlation (R² = 0.93, RMSE = 0.64 t/ha). This study demonstrates the potential of combining S2-derived indices and crop model-derived indices to construct an enhanced yield prediction model suitable for fields in diversified climate conditions.

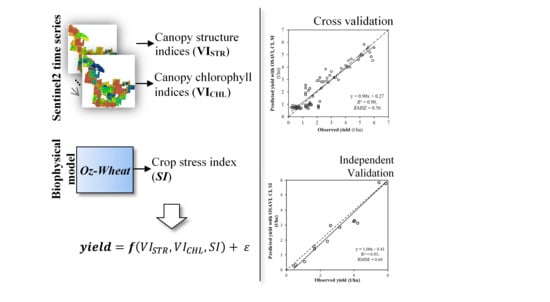
1. Introduction

Wheat (Triticum aestivum L.) is the 5th largest staple crop consumed by people worldwide [1]. Global wheat consumption reached a record high of 736 million tonnes in 2016/2017, which is a growth of 25% during the past 15 years (www.nass.usda.gov). In addition, while the rate of increase in global cereal yields has slowed or stagnated, the demand for wheat is projected to increase in future as the global population increases [2]. Therefore, the sustainable production of wheat will have a crucial bearing on food security over the coming decades.

In Australia, wheat is the main winter crop and contributes significantly to the national economy [3]. Significant volatility exists in wheat production due to large fluctuations in yield and area planted across the broad cropping region of Australia, often associated with the high climatic variability arising from El Niño or La Niña events [4]. Within this context, crop prediction has proved to be a valuable tool in assisting decision makers at a range of scales to improve yield outcomes and enhance profitability [5,6]. However, there are few existing systems capable of accurately predicting yield at field or within field scales across production regions. Crop productivity influences the entire supply chain so that accurate and timely monitoring of crops and early prediction of yield are crucial for crop management, marketing, insurance and financial decisions. Early information on possible crop failures and potential yield reductions could aid policy and decision making aimed at moderating consequences of serious production shortages.

Currently, a range of techniques has been adopted for early estimation of broad-scale crop yields. They can be broadly categorized into three groups: (1) field surveys, (2) remote sensing (RS) methods, and (3) crop modelling (or in combination with 2). Firstly, field survey based approaches using random sampling techniques are practiced in many countries across the world. Detailed household data can be collated to develop forecasts at regional and national levels (e.g., HarvestChoice, https://harvestchoice.org). However, the method has drawbacks: it is costly, time-consuming, and has poor accuracy when there are insufficient field observations. Further, results are usually not released until three to five years after the crop has been harvested, making them of no use for real time issues [7,8].

RS methods for crop monitoring and yield estimation have been developed over the past four decades due to its potential to provide accurate and timely information during the crop growth period. Various studies have demonstrated reasonable potential for using RS within a theoretical yield prediction framework to estimate yield and gross primary production [9]. However, direct theoretical approaches require detailed data at daily time steps as well as assumptions on fraction of absorbed photosynthetic radiation, radiation use efficiency, and harvest index, which limit operational application at the field scale over large areas [10,11].

A number of studies have reported empirical yield models based on a range of RS-derived vegetation indices (VI) [12,13,14,15]. The principle behind relating remotely sensed VI with yield is that crop yield is a function of canopy characteristics including canopy architecture (e.g., LAI), biomass, and chlorophyll content. RS captures the total reflectance response (reflectance, transmission, and absorbance) at the canopy level, which can be related to canopy attributes (biochemical, physiological and morphological). For canopy structure, the Normalized Differential Vegetation Index (NDVI), Simple Ratio (SR), Enhanced Vegetation Index (EVI) and optimized soil-adjusted vegetation index (OSAVI) are derived from reflectance in the red (R) and near-infrared bands (NIR), which are affected by both pigment absorption (R) and the scattering effect (NIR) [16,17,18,19]. Zhao et al. [20] found that canopy reflectance at flowering (measured as NDVI and EVI) was significantly correlated with irrigated cotton yield (R² ranged from 0.56 to 0.89). Similar significant correlations of structural indices at 65–75 days after green up have been found with maize yield and at 80 days after green up in the case of soybean yield [21]. However, these approaches have not been applied at the field scale due to issues with spatial and temporal precision [13,14,15,22,23]. A number of studies have also utilized multispectral and/or hyperspectral sensing and showed high efficacy in predicting chlorophyll and nitrogen concentrations within the crop canopy. Such approaches enable the successful detection of morphological, physiological and biochemical processes resulting in crop stresses that potentially affect final crop yield [24,25,26,27].

Although traditional VIs have been successfully applied for estimating yield and crop monitoring, their accuracy and application are frequently limited by either coarse spatial resolution (e.g., 250–1000 m of MODIS), inadequate temporal coverage (e.g., theoretically 16 days for Landsat), and limited spectral bands and band widths. These aspects constrain the development of application-ready products from RS platforms.

Predicting crop yields utilizing crop models has achieved some success [28]. However, due to an even greater demand on accurate parameterization and data inputs at the local scale, potential for predicting yield accurately at the field scale across large regions is limited [22,29]. To address the lack of accurate input parameters at the field scale, Lobell et al. [15] proposed an integrated approach with some success. This approach used leaf area index (LAI) estimates from satellite imagery to select and update the most likely crop growth and yield simulation at the pixel scale from a plethora of simulations generated using the Agricultural Production Systems Simulator (APSIM) crop modelling platform [15].

The launch of Sentinel 2 (S2) in 2015 provided the opportunity to overcome the identified constraints via its high spatial (10 m to 60 m), spectral (13 bands) and temporal resolutions (five-day return periods). S2 carries a multispectral instrument (MSI) payload that samples 13 spectral bands (https://sentinel.esa.int). With four bands in the visible to near-infrared range at 10 m resolution, four bands in the red edge range at 20 m resolution, two bands in the short-wave range at 20 m resolution and three bands at 60 m, it provides opportunity to explore new frontiers in crop yield prediction. Currently S2 can provide imagery every five days under ideal circumstances, which facilitates characterizing the entire crop life cycle at high temporal resolution. Some studies have utilized and validated the potential for using S2 for land cover classification [30], crop mapping [31,32], canopy chlorophyll and nitrogen content quantification [33,34] and yield estimation of other crops, with reasonable success [35,36,37,38].

Despite these advantages, cloud contamination on the optical images may still result in insufficient data for capturing the stresses experienced by a crop, especially those around flowering and during grain filling that crop will reduce grain number and weight and thus total grain yield [39]. Previous research has successfully estimated crop stress status during these critical periods using the thermal bands from Landsat [14] or via a simulated crop stress index derived from crop models as long as suitable weather data are available [12]. However, the use of Landsat imagery is usually constrained by missing data due to its low temporal frequency and cloud cover.

The aim of this study was to investigate the potential to utilize S2 MSI imagery for predicting dryland wheat yields at the field scale in North Eastern Australia (NEAUS). Firstly, VIs and crop growth attributes were derived from S2 time series. Secondly, the capacity of these VIs and crop growth attributes to predict wheat yield at the field scale was assessed. Thirdly, the potential to improve yield prediction by integrating a crop stress index simulated from the shire scale Oz-wheat model with VIs was explored. The predictive models were developed using data from 89 fields across two diverse cropping seasons in NEAUS. The models were contrasted quantitatively, and their robustness was evaluated using data from 14 independent fields at different locations. The implications and utility to industry of the findings of this study were discussed.

2. Study Area

Field data for model training was acquired from a broad acre cropping farm located in the Moree Plains Shire in Northern New South Wales (Figure 1). Cropping systems on this farm are mixed dryland winter cereals and irrigated summer cotton. Total area of the property is 24,000 ha—of which, 10,400 ha is winter wheat, grown in rotation with cotton. During a normal season, only half of the irrigated area is cropped at any one time, with the other half maintained as a bare fallow. Summer cotton is usually planted during October, while winter wheat is sown in May to June and harvested during November.

Long-term weather records (available from 1995 to present) from the nearest meteorological station (Moree Aero, ~30 km from the farm; latitude: 29.49°S, longitude: 149.85°E, elevation: 213 m), showed an average rainfall of 576 mm, with substantial within- and between year variations. Annual rainfall was 527 mm (323 mm in-crop) and 512 mm (120 mm in-crop) for 2016 and 2017, respectively. However, the two years experienced significantly high within-season variability. During 2016, rainfall mainly occurred during the winter crop-growing period with the highest amount recorded in September. Conversely, for 2017, the highest rainfall amount occurred during the fallow period before sowing (March) and significantly lower rainfall was observed during the winter crop-growing period. At the same time, maximum temperature during 2017 was significantly higher than that of 2016 (Figure 2a). This resulted in two significantly diverse cropping seasons and thus an ideal data set for model calibration and training.

Additional field data from fields located in Moree Plain Shire (close to the training fields) and Bendemere Shire in South-eastern Queensland was collected for independent model validation. Climate records at Somerset station (next to the selected fields in Bendemere, latitude: 26.47°S, longitude: 148.97°E, elevation: 354 m) show that annual rainfall there was 628 mm (310 mm in-crop) and 465 mm (205 mm in-crop) for 2016 and 2017 season, respectively. This variation was similar to that observed for the training fields (Figure 2b). As a result, while model testing was done on a completely independent data set from that of the training data set, both had similar dry land cropping environments. However, the independent test ensures model robustness and utility in application when out scaling to different regions and seasons.

3. Data and Processing

3.1. Yield Data

The wheat yield data at the field scale was acquired from the Sundown Pastoral Company Pty. Ltd. This data was collated by yield monitors mounted on a combine harvester. Field-scale yield was aggregated from point-scale recordings at approximately 2 m intervals. In total, yield data (t/ha) for 46 fields (total area 5013 ha, field area ranging from 8 to 832 ha) in the 2016 crop season and 43 fields (total area 4714 ha, field area ranging from 6 to 554 ha) in the 2017 crop season constituted the training data set for model development and calibration (Figure 1). Yield ranged from 2 to 6 t/ha in 2016 and 0.2 to 2.3 t/ha in 2017.

The calibrated model was then validated on a completely independent data set that had a total of 14 fields for the 2016 and 2017 seasons. Eight of these fields with yield data collected in 2016 (total area 1312 ha, field area ranging from 44 to 379 ha) were located in Moree Plains Shire (30 km away from the training fields). The remaining six fields for 2017 season (total area 572 ha, field area ranging from 18 to 215 ha) were located 320 km away in Bendemere Shire in Queensland (Figure 1). Averaged yield was 1.3 t/ha and 4.3 t/ha for the 2016 and 2017 fields, respectively.

3.2. Satellite Imagery and Atmospheric Corrections

All available S2 Top-Of-Atmosphere (TOA) reflectance scenes covering the farms (29.34°S–29.56°S, 149.42°E–149.66°E) for 2016 and 2017 were downloaded through Google Earth Engine (GEE). Scenes with cloud coverage greater than 30% were excluded from the analysis. The time series encompassed 14 and 25 scenes for 2016 and 2017 winter crop seasons, respectively (

Table 1. List of Sentinel-2 MSI imagery * dates used for the model calibration and validation sets.

Cropping Season	Date/Month
Calibration
2016	14/01, 23/02, 14/03, 13/04, 13/05, 02/06, 01/08, 21/08, 10/09, 20/10, 19/11, 09/12, 19/12, 29/12
2017	18/01, 07/02, 17/02, 09/03, 18/04, 08/05, 28/05, 17/06, 02/07, 22/07, 27/07, 11/08, 16/08, 31/08, 05/09, 20/09, 10/10, 30/10, 04/11, 09/11, 24/11, 09/12, 14/12, 19/12, 29/12
Validation
2016	13/05, 01/08, 21/08, 20/10
2017	02/07, 22/07, 27/07, 11/08, 16/08, 31/08, 05/09, 20/09

* Images that were 70% or more cloud free were used in this analysis.

).

The collected S2 TOA reflectance were corrected to surface reflectance using a 6S (Second Simulation of the Satellite Signal in the Solar Spectrum) atmospheric correction approach [40]. Py6S, an interface to the 6S through Python programming language, was implemented to perform the correction within GEE [41,42]. The atmospheric condition for each image scene (i.e., water vapor, ozone and aerosol optical thickness values) were determined using data products that are available in GEE.

3.3. Selection of Vegetation Indices

A total of 14 spectral VIs were explored to determine their efficacy in accounting for wheat yield variability among fields (Table 2). VIs are transformations of multiple spectral bands and wavelengths that allow the interpretation of variations in canopy structural and photosynthetic activities [16]. Here, we grouped the 14 selected indices into two categories as “canopy structural indices” (VI_STR) and “chlorophyll indices” (VI_CHL), based on their differences in wavelengths used (Table 2).

Six VI_STR indices were used to test the contribution of canopy structure to final yield. These indices are mainly known for their ability to capture light properties within the visible and near-infrared spectral regions. The Simple Ratio (SR) is sensitive to green vegetation and is highly correlated with LAI and leaf biomass [43]. NDVI is widely known for its capacity for assessing regional and global vegetation fluctuations. However, it is more sensitive to reflectance from soil background and also tends to saturate for high biomass canopies [16]. The Difference Vegetation Index (DVI) is a simple index but very sensitive to changes in soil background [44]. The optimized soil-adjusted vegetation index (OSAVI) is a soil-adjusted vegetation index optimized for agricultural monitoring, which has been applied to estimate crop canopy cover and monitor crop growth [45]. The Enhanced Vegetation Index (EVI) is an optimized vegetation index that shows improved sensitivity for measuring terrestrial vegetation that has high biomass or LAI, while better accounting for canopy background and atmosphere influences [16]. Lastly, the Enhanced Vegetation Index 2 (EVI2) is a transformation of the EVI, but without blue band [46].

Eight VI_CHL indices and their ability to predict final wheat yield were also tested. Canopy chlorophyll content is strongly related to nitrogen supply and is therefore a strong predictor for crop yield [47]. Most chlorophyll-related indices focus on capturing reflectance in regions of the electromagnetic spectrum where (1) chlorophyll absorption is greatest, i.e., red band (R) region, (2) reflectance drastically increases towards the near-infrared band, i.e., red edge (RE) band region, and (3) the leaf cell structure produces strong reflection, i.e., near-infrared band region (NIR). Details of all indices tested in this study are listed in Table 2.

Table 2. Details of selected canopy structural- and chlorophyll-related spectral indices tested in this study. The term “R_Bi” in the equations denotes the surface reflectance at corresponding Sentinel-2 bands used for calculating the indices.

Index	Equation	Reference
Canopy structural-related indices( VISTR)
Normalized Difference Vegetation Index (NDVI)	$NDVI=\left(R_{B8}-R_{B4}\right)/\left(R_{B8}+R_{B4}\right)$	[44]
Optimized soil-adjusted vegetation index (OSAVI)	$$\begin{gathered} OSAVI \\ =1.16\times \left(R_{B8}-R_{B4}\right)/\left(R_{B8}+R_{B4}+0.16\right) \end{gathered}$$	[48]
Simple ratio (SR)	$SR=R_{B8}/R_{B4}$	[49]
Difference Vegetation Index (DVI)	$DVI=R_{B8}-R_{B4}$	[44]
Enhanced Vegetation Index (EVI)	$EVI=2.5\times \left(R_{B8}-R_{B4}\right)/\left(R_{B8}+6\times R_{B4}-7.5\times R_{B2}+1\right)$	[16]
Enhanced Vegetation Index 2 (EVI2)	$EVI2=2.5\times \left(R_{B8}-R_{B4}\right)/\left(R_{B8}+2.4\times R_{B4}+1\right)$	[46]
Chlorophyll-related indices(VICHL)
Chlorophyll Index red edge (CIrededge)	$C{I}_{rededge}=R_{B7}/R_{B5}-1$	[50]
Transformed Chlorophyll Absorption in Reflectance Index (TCARI)	$TCARI=3\times \left[\left(R_{B5}-R_{B4}\right)-0.2\times \left(R_{B5}-R_{B3}\right)\times \left(R_{B5}/R_{B4}\right)\right]$	[51]
TCARI/OSAVI (TO)	$TO=TCARI/OSAVI$	[51]
Green chlorophyll vegetation index (GCVI)	$GCVI=R_{B8}/R_{B3}-1$	[52]
Green Difference Vegetation Index (GDVI)	$GDVI=R_{B8}-R_{B3}$
Normalized difference red edge 1 (NDRE1)	$NDRE1=\left(R_{B6}-R_{B5}\right)/\left(R_{B6}+R_{B5}\right)$	[53]
Normalized difference red edge 1 (NDRE2)	$NDRE2=\left(R_{B7}-R_{B5}\right)/\left(R_{B7}+R_{B5}\right)$	[53]
Canopy Chlorophyll Content Index (CCCI)	$CCCI=NDRE1/OSAVI$	[54]

Table 2. Details of selected canopy structural- and chlorophyll-related spectral indices tested in this study. The term “R_Bi” in the equations denotes the surface reflectance at corresponding Sentinel-2 bands used for calculating the indices.

Index	Equation	Reference
Canopy structural-related indices( VISTR)
Normalized Difference Vegetation Index (NDVI)	$NDVI=\left(R_{B8}-R_{B4}\right)/\left(R_{B8}+R_{B4}\right)$	[44]
Optimized soil-adjusted vegetation index (OSAVI)	$$\begin{gathered} OSAVI \\ =1.16\times \left(R_{B8}-R_{B4}\right)/\left(R_{B8}+R_{B4}+0.16\right) \end{gathered}$$	[48]
Simple ratio (SR)	$SR=R_{B8}/R_{B4}$	[49]
Difference Vegetation Index (DVI)	$DVI=R_{B8}-R_{B4}$	[44]
Enhanced Vegetation Index (EVI)	$EVI=2.5\times \left(R_{B8}-R_{B4}\right)/\left(R_{B8}+6\times R_{B4}-7.5\times R_{B2}+1\right)$	[16]
Enhanced Vegetation Index 2 (EVI2)	$EVI2=2.5\times \left(R_{B8}-R_{B4}\right)/\left(R_{B8}+2.4\times R_{B4}+1\right)$	[46]
Chlorophyll-related indices(VICHL)
Chlorophyll Index red edge (CIrededge)	$C{I}_{rededge}=R_{B7}/R_{B5}-1$	[50]
Transformed Chlorophyll Absorption in Reflectance Index (TCARI)	$TCARI=3\times \left[\left(R_{B5}-R_{B4}\right)-0.2\times \left(R_{B5}-R_{B3}\right)\times \left(R_{B5}/R_{B4}\right)\right]$	[51]
TCARI/OSAVI (TO)	$TO=TCARI/OSAVI$	[51]
Green chlorophyll vegetation index (GCVI)	$GCVI=R_{B8}/R_{B3}-1$	[52]
Green Difference Vegetation Index (GDVI)	$GDVI=R_{B8}-R_{B3}$
Normalized difference red edge 1 (NDRE1)	$NDRE1=\left(R_{B6}-R_{B5}\right)/\left(R_{B6}+R_{B5}\right)$	[53]
Normalized difference red edge 1 (NDRE2)	$NDRE2=\left(R_{B7}-R_{B5}\right)/\left(R_{B7}+R_{B5}\right)$	[53]
Canopy Chlorophyll Content Index (CCCI)	$CCCI=NDRE1/OSAVI$	[54]

4. Methods

4.1. Overview

Here, we employed a three-step approach: (i) construction of indices, (ii) analysis and model calibration and (iii) model validation. The first step was used to derive VI time series and to calculate attributes reflecting crop canopy development (e.g., canopy green up, senescence and peak) using the VI time series. During this step, we also simulated the crop stress index. The second step involved the development of the field-scale model. The model validation step was used to test model robustness and predictive ability for an independent set of fields. For creating the VI time series, we reconstructed the time sequential images acquired from the atmospheric corrected S2 MSI imageries. Metrics associated with peak canopy values and metrics relating to rates of green up and senescence (based on the regression slopes) before and after the peak were then calculated. Two crop stress indices (water stress and canopy temperature) were calculated using the biophysical crop model (Oz-Wheat, for water stress) and Landsat 8 imagery (for canopy temperature), respectively. The yield prediction model was developed using statistical analysis of variance (ANOVA) and a multivariate analysis incorporating all derived metrics and indices.

4.2. Extraction of Canopy Development-Related Metrics

Metrics derived from the S2 VI time series included peak, rate of green up (R_GU) and rate of senescence (R_SEN). Peaks of canopy values were derived by calculating the maximum value of each VI index derived from S2 time series between end of May and early November each year. May to November encapsulated the full crop growth period for winter crops in the study and training sites. The VIs were calculated according to their definitions outlined in Table 2 using GEE. Field-scale VIs were aggregated from the pixels within each field, as defined by field boundaries. The boundaries were provided by the field data producer and their accuracy was visually checked against S2 images showing clear field extensions. The derived VI series were then analyzed with the ArcGIS platform (Esri Inc., Version10.6.1).

The NDVI time series was divided into two portions before and after the date at which peak NDVI was observed. All available dates between start to the peak NDVI and peak to end were used to fit regression lines between NDVI values and date. The slopes of the fitted lines constituted the R_GU (before peak) and the R_SEN (after peak). These metrics enabled the accurate detection of the growth rates (before and after peak), and magnitude and exact timing of full canopy for each field crop. These three metrics (peak, R_GU and R_SEN) closely mimic crop phenology attributes and therefore likely increase the discriminative power in predicting crop yield responses (e.g., timing of flowing and vegetative and grain filling phases) to environmental conditions.

4.3. Calculation of Crop Stress Using Biophysical Model

We investigated the ability of two crop stress-related metrics to predict variations in field-scale wheat yields. These were (i) the simulated Crop Stress Index (SI), which relates strongly to stress due to water limitation in dryland cropping regions, and (ii) land surface temperature (LST), which is a surrogate for crop stress and a measure of transpiration restriction at the canopy level.

SI was determined via an existing optimization calibration approach to determine the level of water supply to demand ratio experienced during crop growth [3,55] given as:

$$SI=E_a/E_t$$

(1)

Here, E_a is the actual evapotranspiration and E_t is the potential evapotranspiration. This ratio qualifies crop water stress and relates well to the physiological responses of a crop to water deficit. This index is simulated with the Oz-wheat model on a daily time step and averaged over an optimized critical period during crop growth around flowering. SI has values ranging from 0 to 1, where a SI value of 1 (E_a = E_t) indicates no water limitation and values below 1 indicate increasing water stress experienced by the wheat crop [3,55].

Oz-wheat is a simple daily time-step model adapted from an agro-climatic wheat stress index model [56,57,58], which is sensitive to a water deficit or excess during the growing season. The model input parameters for each shire (i.e., potential available water content, planting rain and stress index period) have been selected based on the best fit when calibrated against actual shire wheat yields from the Australian Bureau of Statistics for the period 1976–2000, 2005, 2010 and 2015. More details on the development and function of the SI within Oz-wheat can be found in Potgieter et al. [56]. This study used the Oz-wheat model to simulate aggregated SI values for Moree Plains (total cropping area 1.1 × 10⁶ ha, data derived from www.agriculture.gov.au) and Bendemere (total cropping area 4.2 × 10⁴ ha) over the 2016 and 2017 cropping seasons. The daily SI was simulated for each of the 15 and 4 climate stations within the cropping area for the Moree Plains (approximately 72,000 ha per station) and Bendemere (approximately 10,000 ha per station) shires, respectively. The model integrates information from each station to a shire level driven by water deficits, historical climate data, three fixed crop maturities (i.e., late, medium, quick; derived from APSIM [59]) and a dynamical sowing date criteria triggered by a rainfall threshold of 15 mm in a five day period.

4.4. Calculation of Crop Stress Using Thermal Imagery

The second crop stress approach involves calculating the land surface temperature, which is known to be highly correlated to crop stress at canopy and field levels. High temperatures during grain filling are known to reduce potential wheat yields [60,61]. We used available Landsat thermal band to characterize canopy thermal conditions during a critical period around peak canopy cover (+/− 20 days). Canopy surface temperature during the period was determined using the Planck function:

$$\mathrm{LST}=\mathrm{K}2/\ln \left(\frac{\mathrm{K}1\times \mathsf{\epsilon }}{C{V}_R}+1\right)$$

(2)

Here, LST is the land surface temperature in degrees Kelvin, CV_R is the cell value as radiance, and $\mathsf{\epsilon }$ is the emissivity, which was set as 0.95 in this study [62]. K1 (774.89) and K2 (1321.08) are thermal conversion constants. Maximum (LST_max), minimum (LST_min) and average (LST_mean) temperatures during the period were then determined by an overlay analysis in ArcGIS (Esri Inc., Version10.6.1).

4.5. Approaches for Estimating Wheat Yield at the Field Scale

We investigated the ability of S2 VI time series-derived canopy development-related metrics and the proposed SI to determine the variance explained and accuracy of wheat yields at the field scale. The metrics and SI were related to field-scale yields using a linear regression model (Equation (3)).

Furthermore, we analyzed the ability when combining the structural and chlorophyll indices to predict field-scale wheat yield. (Equation (4)). Finally, SI was included with and without the VIs models to determine the likely contribution of crop water stress status during flowering and grain filling at the field scale (Equation (5)).

$$Yield=a+b\times \left[peak V{I}_{STR},V{I}_{CHL}, R_{GU},R_{Sen}\right]$$

(3)

$$Yield=a+b\times peak V{I}_{STR}+c\times peak V{I}_{CHL}$$

(4)

$$Yield=a+b\times peak V{I}_{STR}+c\times peak V{I}_{CHL}+d\times SI$$

(5)

where a, b, c and d are the regression coefficients for each predictor. The coefficient of determination (R²), the prediction error (root mean square error, RMSE) and statistical significance of the model were computed to assess the performance of each index and phenological metric. Yield data for the 89 fields (46 in 2016, 43 in 2017) were used to calibrate the models.

4.6. Model Validation and Accuracy

A cross-validation approach was employed to determine the robustness and goodness of fit of the yield models. Yield data for the 89 fields was randomly partitioned into 10 “folders”. A single “folder” was retained as the cross-validation data for testing the model, with yield data in the remaining nine folders used as training data to fit the model. This cross-validation procedure was repeated 10 times to constitute the cross-validated R² and RMSE [63].

Model accuracy was determined for each model by using the Mean Absolute Percent Error (MAPE) metric. MAPE was then transformed into a percentage as follows:

$$MAPE=\frac{\left|A_t-F_t\right|}{\left|A_t\right|}\times 100\%$$

(6)

where A_t represents the actual yield and F_t is the predicted yield.

For validation, we applied the best derived model to predict observed yields for the independent validation dry land cropping data set (14 fields).

5. Results

5.1. Simulated Crop Stress and Observed Yield across Seasons

The simulated SI values for the training data set located in Moree Plains Shire were 0.95 (little stress) and 0.59 (moderately stressed) for 2016 and 2017, respectively. These values varied between the two years and reflected the crop stress experienced by the crop at flowering and grain filling due to water limitation. The simulated stress aligned well with the total rainfall recorded during the in-crop period. Specifically, rainfall from May through October (323 mm) was 46% above the average (221 mm) and accounted for 61% of the total annual rainfall received during 2016. Conversely, 77% of the rainfall occurred during the non-cropping period (fallow), while extremely low rainfall occurred during the booting to flowering period in 2017 (Figure 2).

Consequently, large differences in wheat yields were observed between the two cropping seasons across fields. The average wheat yield (46 fields) for 2016 was 4.12 t/ha, while much lower yields were observed in the 2017 cropping season, with an average of 1.14 t/ha (Figure 3). The wide distribution of yields across fields and between the two seasons provided an ideal training data set for developing a predictive yield model that can be used across diverse environmental conditions and crop management practices.

5.2. Field-Scale Yield Prediction Approaches

5.2.1. Predicting Yield Using Single Canopy Development-Related Metrics

Overall, both VI_STR- and VI_CHL-derived peaks showed moderately strong linear relationships with field-scale wheat yields, while R_GU and R_SEN showed slightly weaker relationships. Specifically, both Peak_OSAVI and Peak_NDVI had similar and moderately high linear correlations in predicting field-scale wheat yields (R² = 0.74, RMSE = 0.91 t/ha, p < 0.001,

Table 3. Linear regression statistics for structural, chlorophyll and phenological metrics to predict actual wheat yields at the field scale.

Index	R2	RMSE (t/ha)	p	Index	R2	RMSE (t/ha)	p
Canopy structural-related indices				Chlorophyll-related indices
PeakOSAVI	0.74	0.91	5.81 × 10−27	PeakCI	0.76	0.88	2.55 × 10−28
PeakNDVI	0.74	0.91	8.11 × 10−27	PeakNDRE1	0.76	0.88	2.83 × 10−28
PeakSR	0.73	0.92	2.07 × 10−26	PeakNDRE2	0.74	0.91	4.43 × 10−27
PeakEVI2	0.72	0.93	5.76 × 10−26	PeakGCVI	0.72	0.93	4.93 × 10−26
PeakEVI	0.72	0.94	8.19 × 10−26	PeakTCARI	0.55	1.19	1.20 × 10−16
PeakDVI	0.70	0.96	9.69 × 10−25	PeakGDVI	0.68	0.99	1.55 × 10−23
				PeakTO	0.34	1.44	1.70 × 10−09
Crop development metrics
Green up rate	0.49	1.22	1.26 × 10−13
Senescence rate	0.56	1.14	4.05 × 10−16

& Figure 4a). Peak_EVI, Peak_EVI2, Peak_SR and Peak_DVI showed slightly lower correlations and higher RMSE compared to Peak_OSAVI and Peak_NDVI.

The best chlorophyll model was obtained when using Peak_CI (R² = 0.76, RMSE = 0.88 t/ha). Equally, Peak_NDRE1 and Peak_NDRE2 showed similar correlation coefficients. TCARI, which is specifically designed for detecting chlorophyll status, did not show improved prediction accuracy, nor did its combination with OSAVI (i.e., TCARI/OSAVI). The metrics capturing the rates of canopy development before (R_GU) and after (R_SEN) full canopy had moderate correlation with yield (R² < 0.56). The R_GU metric had much lower skill (R² = 0.49) than the peak VI metrics (R² > 0.91) in predicting final yield. Further research is required if better prediction of yield at the field scale is required well in advance of flowering.

5.2.2. Predicting Wheat Yield Using Combined Model

A multivariate analysis was conducted to determine the best combination of VI_STR and VI_CHL to predict field-scale wheat yields. Overall, “Peak_OSAVI + Peak_CI” and “Peak_NDVI + Peak_CI” were the two combinations showing highest correlations with field yields. All models showed similar RMSEs between 0.84 to 0.86 t/ha (

Table 4. Multivariate linear regression analysis for combined models. The models including SI are highlighted in grey.

Index Combinations	R2	RMSE (t/ha)	p
Canopy structural-related index + chlorophyll-related index
PeakOSAVI + PeakCI	0.77	0.86	2.56 × 10−28
PeakOSAVI + PeakNDRE1	0.76	0.86	4.75 × 10−28
PeakNDVI + PeakCI	0.78	0.84	6.82 × 10−29
PeakNDVI + PeakNDRE1	0.76	0.88	1.05 × 10−27
Canopy structural-related index + chlorophyll-related index + SI (or LST)
PeakOSAVI + PeakCI + SI	0.91	0.54	2.10 × 10−42
PeakOSAVI + PeakNDRE1 + SI	0.86	0.66	8.53 × 10−36
PeakNDVI + PeakCI + SI	0.91	0.54	3.80 × 10−42
PeakNDVI + PeakNDRE1 + SI	0.88	0.61	2.54 × 10−38
PeakOSAVI + PeakCI + LSTmax	0.85	0.71	5.68 × 10−29
PeakOSAVI + PeakCI + LSTmean	0.69	1.04	1.87 × 10−19

). The strongest relationship was observed for the model using Peak_NDVI and Peak_CI to predict wheat yield (R² = 0.78, RMSE = 0.84 t/ha). Auto-correlations between indices (at peak) ranged from R² = 0.70 (NDVI~SR) to R² = 0.99 (EVI ~ EVI2), and R² = 0.29 (TCARI ~ TCARI/OSAVI) to R² = 0.99 (NDRE1 ~ NDRE2) for structural and chlorophyll indices, respectively. The correlation between Peak_OSAVI and Peak_CI was 0.90, while correlation between Peak_NDVI and Peak_CI was 0.85.

Adding SI to the models generated above further improved the correlations (R²) by more than 12% across all models. Typically, either Peak_OSAVI or Peak_NDVI with Peak_CI and SI showed substantially higher R² of 0.91 for predicting wheat yields - including SI as a covariate improved the model strength (in terms of R²) by more than 18% compared to omitting it. At the same time, the error decreased by around 37% from 0.86 t/ha to 0.54 t/ha. Adding crop stress derived from Landsat LST (LST_max and LST_mean) during the critical period around peak canopy resulted in lower R² and larger RMSE when combined with the other main structural and chlorophyll indices (Table 4). The R² values between actual yield and LST_max and mean of LST_mean around peak canopy were 0.76 and 0.47, respectively. Hence, LST was not included for final model development and validation.

5.3. Model Calibration and Validation

Predicted versus observed yield relationships for the calibration field data are shown in Figure 5 for the field-scale wheat yield models with best fit (Equations (7) and (8)).

$$\mathrm{Yield}=-2.18-2.39\times Pea{k}_{OSAVI}+0.82\times Pea{k}_{CI}+5.13\times SI$$

(7)

$$\mathrm{Yield}=-2.15-1.69\times Pea{k}_{NDVI}+0.74\times Pea{k}_{CI}+5.15\times SI$$

(8)

Both models showed significantly high cross-validated correlation for predicting field-scale wheat yield. For Peak_OSAVI and the Peak_CI in combination with the SI, the correlation was high (R² = 0.90), with a small prediction error (RMSE = 0.56 t/ha). The MAPE ranged from close to 0% to 273% and averaged 33% across all fields and years. Average MAPE was 10% and 59% for the 2016 and 2017 cropping season, respectively. It is important to note that fields showing high MAPE% values had small portions within the fields with extremely low observed yields. For example, there are four fields (in 2017) with observed yields less than 0.3 t/ha and the MAPEs for these fields ranged from 146% to 273%. These fields had extremely low peak values in OSAVI and NDVI but were not excluded for completeness (data not shown). When excluding these fields with high MAPE%s (e.g., MAPE > 50%), the average yield for 2017 fields was recorded at 1.2 t/ha and the MAPE averaged 28%. Conversely, for the 2016 season, MAPEs for the fields ranged from 0.2% to 47% with most of the fields (40 out of 46 fields) showing MAPE values well below 20% at the field scale.

Similarly, the modelled yields using Peak_NDVI, Peak_CI and simulated SI was consistent with the observed values (R² = 0.90, RMSE = 0.57 t/ha). The MAPE ranged from close to 0% to 316% across fields and years. Average MAPE were 11% and 57% for the 2016 and 2017 cropping season, respectively. Again, larger predict errors (i.e., high MAPE values) were associated with fields that had extremely low observed yields. This was evident for the 2017 cropping season (d). The relative poorer performance in predicting fields that have extremely low yields (< 1 t/ha) does not necessarily suggest that the sensing indices are unable to detect those lower peaks (at pixel scales). The phenomenon is more likely related to poor crop emergence (crop cover) or completely failed crops within a field due to various biotic (pests and diseases) or abiotic stresses (water, high temperatures, soil constraints) [54]. Operationally, such pixels with low peak values will be excluded when aggregating to a field level. However, for exemplifying the sensitivity of indices and completeness of our analysis, pixels with low peak values in crop canopies were retained.

Predictive models were tested using an independent data set. Both models showed significantly high correlations in predicting wheat yield for the independent test data set (Figure 6). Specifically, the OSAVI based model in combination with Cl and SI showed high correlation coefficient (R² = 0.93, RMSE = 0.64 t/ha). Similarly, the NDVI, CI and SI model had an R² of 0.93, RMSE of 0.63 t/ha and an average the MAPE of 20%. Although both models had predictions close to the 1:1 line (broken line Figure 6a,c), there was a slight underestimation for observed yields less than 2 t/ha. Furthermore, relatively large aggregated errors, greater than 30% (MAPE), were mainly related to field with observed yields less than 1 t/ha.

5.4. Within-Field Scale Application of Combined Model

The NDVI-based model (Equation (7)) was applied to the time series of S2 imagery for each pixel. Figure 7 shows the predicted yields for each pixel and the MAPE of aggregated predicted yield versus observed yield for each field. Substantial within-field variation was captured using the predictive yield model at the pixel scale. A pixel-scale yield map for the 2017 wheat fields is include as Figure S1.

6. Discussion

This study investigated potential of combining high-resolution S2 imagery and crop modelling to predict wheat yield at the field scale. Here, we analyzed the sensitivity of VI and remotely sensed crop development metrics to predict actual wheat yields. The chlorophyll-related indices (Peak_CI and Peak_NDRE) had similar or slightly higher R² than the structural VIs. Previous studies have reported similar findings, i.e., changes in red edge-based indices had a strong linear correlation with canopy chlorophyll content and thus better ability to predict yield [34,64,65]. While time series CI-derived metrics are useful indicators of crop canopy health and nitrogen status that can have large effects on biomass accumulation, grain formation and ultimate final yield [34], our results indicate similar predictive skill with better structural- and chlorophyll-related indices.

Combining VIs related to structural and chlorophyll content resulted in a small increase in overall predictive skill for actual yields at the field scale compared to using only structural VIs. Because both structural and chlorophyll VIs respond to different aspects of plant processes during crop growth (i.e., morphological and physiological), both were included in the final models. Further, for considering regions outside the calibration location and diverse crop management practices (such as modern cultivars with targeted stay-green traits [66]), a more comprehensive model was desirable.

The final model incorporated crop stress-related metrics (i.e., temperature and SI) with structural and chlorophyll VIs. Inclusion of temperature from Landsat imagery and the simulated crop stress (SI) increased the overall performance of the wheat yield model, with the latter being more effective. Such indices are known to be able to mimic crop stresses due to high temperature and/or water limitation, specifically around flowering and during grain filling, where they cause a reduction in final wheat yield [60,61]. Furthermore, the SI lends itself to higher utility in an operational sense for predicting crop yields well before peak canopy, which is not at all possible with a “pure” RS approach using LST and vegetation indices. In addition, acquisition of LST data on a regular time scale can be limited due to cloud cover and missing data.

Previous studies have indicated that changes in climate and farm management practices, causing local variations in crop canopies and ensuing crop yields [67,68], would likely affect the applicability of any yield prediction models to other regions and seasons [7,69]. The model developed in this study integrated both structural- and chlorophyll-related indices that are main contributors to final crop potential, with simulated crop stress index that incorporates effects on yield driven by environmental factors such as rainfall and temperature. Part of the model’s discriminative power is driven by the magnitude in the peak of the selected structural and chlorophyll indices. The timing of when the peak occurs can differ between regions mainly due to the interaction between varieties (maturity types) and growing degree days (temperature) [70]. Unfortunately, variety type and sowing date data were not available in this study due to data privacy laws and could therefore not be analyzed. However, it is likely to have little to no effect on the accuracy and application of the derived model since timing is not a covariate of the model. Furthermore, by incorporating the SI as covariate, we accounted for some of the differences in phenology (flowering) and temperature across regions. It is anticipated that utilizing SI at the station level closest to the field will enhance the specificity and accuracy of the yield prediction. Therefore, the method for developing models utilized in this study provided a robust operational framework that could be easily adapted to yield prediction across other regions and seasons. This approach, however, is only applicable to dryland wheat cropping. For irrigated wheat crops that are not water limited, other yield-environment indices such as the photo thermal quotient (PTQ) would need to be explored [71].

Finally, this study exemplified the clear advantage of utilizing the fine spatial resolution of S2 (10 m to 20 m) to predict yield within a field. When applying the field-scale models to predict yield at the pixel level, we found appreciably low MAPEs across the training data set (Figure 7). This approach will have considerable utility for precision agriculture. For example, by identifying the low/medium/high-yield regions within a field (e.g., Figure 7), and their distribution across seasons, it is possible to support approaches to specifically targeted management that might result in higher profitability. Although this study is not exhaustive, it showed high predictability of wheat yields at field and within-field scales from remotely-sensed and modelled indices. Further targeted research will be pursued to explore the utility of these enabling digital technologies to the agricultural industry and government agencies to aid decision making.

7. Conclusions

In this study, we assessed the potential for integrating high-resolution satellite imagery (S2) with crop stress-related indices to predict wheat yield at the field scale. Yield prediction models were developed by deriving the indices relating to canopy structure, chlorophyll canopy status and simulated crop stress. The models were calibrated and validated across a diverse set of environments during the 2016 and 2017 winter cropping seasons in north-eastern Australia.

The final selected model integrating structural, chlorophyll and SI indices showed significant and high cross-validated correlation (R² = 0.90) for predicting field-scale wheat yield. When using the derived model to predict wheat yield for independent fields the correlation remained significantly high (R² = 0.93). From this study, it is clear that a predictive model using a VI or more than one VI (structural and/or chlorophyll) is less accurate than a model combining VIs (structural and chlorophyll) with the simulated SI (crop stress around flowering) to predict final harvested wheat yield. The biophysical index, such as the SI used here, provides an innovative avenue to enhance yield prediction from remote sensing approaches. This is mainly due to SI’s ability to capture crop stress during flowering and grain filling periods in these water-limited environments. It is anticipated that producers, as well as related agricultural industries (e.g., bulk handlers, grain storage, transportation), will be able to utilize these enhanced predictive technologies to achieve reliable and accurate estimates of yield at field and within-field scales. Having access to spatial information on likely crop yields before harvest will not only aid in tactical decisions regarding precision agriculture but will likely aid government and private agencies responsible for commodity market forecasts, crop insurance products, and the collation of commodity forecast information at regional and national scales.