The Climate Monitoring SAF Outgoing Longwave Radiation from AVHRR
Abstract
:1. Introduction
2. Instantaneous OLR Estimation
2.1. Problem Statement
2.2. OLR Regressions
2.3. Results
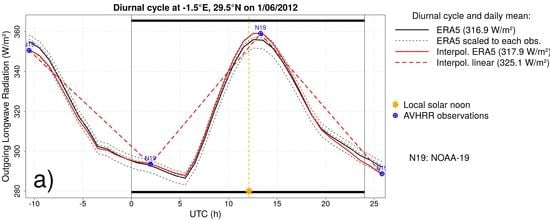
3. Daily and Monthly Mean OLR
3.1. Problem Statement
3.2. Method
3.3. Results
4. Overall Validation with Respect to CERES SYN1deg
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ADM | Angular Dependency Model |
| AVHRR | Advanced Very High Resolution Radiometer |
| Ch4, Ch5 | Channel 4, Channel 5 |
| CDR | Climate Data Record |
| CERES | Clouds and the Earth’s Radiant Energy System (instrument and mission) |
| CLARA | CM SAF cLoud, Albedo and Radiation dataset from AVHRR data |
| CMSAF | Climate Monitoring Satellite Application Facility |
| ECT | Equatorial Crossing Time |
| ERB | Earth Radiation Budget (instrument and mission) |
| ERBE | Earth Radiation Budget Experiment (instrument and mission) |
| FCDR | Fundamental Climate Data Record |
| FM | Flight Model |
| GAC | Global Area Coverage |
| GCOS | Global Observing System for Climate |
| GERB | Geostationary Earth Radiation Budget (instrument and mission) |
| GOES | Geostationary Operational Environmental Satellite |
| IGBP | International Geosphere-Biosphere Programme |
| LST | Local Solar Time |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| MSG | Meteosat Second Generation |
| MVIRI | Meteosat Visible and Infrared Imager |
| NOAA-X | National Oceanic and Atmospheric Administration, Satellite X |
| OLR | Outgoing Longwave Radiation |
| RMSE | Root Mean Square Error |
| RMSE-bc | Bias-corrected RMSE |
| RSF | Reflected Solar Flux |
| SSF | Single Scanner Footprint |
| SYN1deg | Synoptic 1° latitude 1° longitude gridded |
| TOA | Top Of Atmosphere |
| VZA | Viewing zenith angle |
References
- Schulz, J.; Albert, P.; Behr, H.D.; Caprion, D.; Deneke, H.; Dewitte, S.; Durr, B.; Fuchs, P.; Gratzki, A.; Hechler, P.; et al. Operational climate monitoring from space: The EUMETSAT Satellite Application Facility on Climate Monitoring (CM-SAF). Atmos. Chem. Phys. 2009, 9, 1687–1709. [Google Scholar] [CrossRef] [Green Version]
- Cracknell, A.P. Advanced Very High Resolution Radiometer AVHRR; Taylor and Francis: London, UK, 1997. [Google Scholar]
- Karlsson, K.G.; Riihelä, A.; Müller, R.; Meirink, J.; Sedlar, J.; Stengel, M.; Lockhoff, M.; Trentmann, J.; Kaspar, F.; Hollmann, R.; et al. CLARA-A1: The CM SAF cloud, albedo and radiation dataset from 28 yr of global AVHRR data. Atmos. Chem. Phys. Discuss. 2013, 13, 935–982. [Google Scholar] [CrossRef] [Green Version]
- Karlsson, K.G.; Anttila, K.; Trentmann, J.; Stengel, M.; Meirink, J.F.; Devasthale, A.; Hanschmann, T.; Kothe, S.; Jaaskelainen, E.; Sedlar, J.; et al. CLARA-A2: The second edition of the CM SAF cloud and radiation data record from 34 years of global AVHRR data. Atmos. Chem. Phys. 2017, 17, 5809–5828. [Google Scholar] [CrossRef] [Green Version]
- Devasthale, A.; Raspaud, M.; Schlundt, C.; Hanschmann, T.; Finkensieper, S.; Dybbroe, A.; Hörnquist, S.; Håkansson, N.; Stengel, M.; Karlsson, K. PyGAC: An open-source, community-driven Python interface to preprocess more than 30-year AVHRR Global Area Coverage (GAC) data. GSICS Q. Newsl. 2017, 11, 3–5. [Google Scholar]
- Hollman, R.; Schlundt, C.; Finkensieper, S.; Raspaud, M.; Karlsson, K.G.; Stengel, M. ESA Cloud cci: Technical Report on AVHRR GAC FCDR Generation. Technical Report Issue 1, Revision 0, ESA Cloud cci. 2017. Available online: http://www.esa-cloud-cci.org/?q=documentation (accessed on 31 January 2020).
- Akkermans, T.; Clerbaux, N. Narrowband-to-Broadband Conversions for Top-of-Atmosphere Reflectance from the Advanced Very High Resolution Radiometer (AVHRR). Remote Sens. 2020, 12, 305. [Google Scholar] [CrossRef] [Green Version]
- Wielicki, B.A.; Barkstrom, B.R.; Harrison, E.F.; Lee, R.B., III; Smith, G.L.; Cooper, J.E. Clouds and the Earth’s Radiant Energy System (CERES): An earth observing system experiment. Bull. Am. Meteorol. Soc. 1996, 77, 853–868. [Google Scholar] [CrossRef] [Green Version]
- Harries, J.E.; Russell, J.; Hanafin, J.; Brindley, H.; Futyan, J.; Rufus, J.; Kellock, S.; Matthews, G.; Wrigley, R.; Last, A.; et al. The geostationary earth radiation budget project. Bull. Am. Meteorol. Soc. 2005, 86, 945–960. [Google Scholar] [CrossRef] [Green Version]
- Liebmann, B.; Smith, C.A. Description of a complete (interpolated) outgoing longwave radiation dataset. Bull. Am. Meteorol. Soc. 1996, 77, 1275–1277. [Google Scholar]
- NOAA Interpolated Outgoing Longwave Radiation (OLR). National Oceanic and Atmospheric Administration. Available online: https://www.esrl.noaa.gov/psd/data/gridded/data.interp_OLR.html (accessed on 30 January 2020).
- Lee, H.T.; Gruber, A.; Ellingson, R.G.; Laszlo, I. Development of the HIRS outgoing longwave radiation climate dataset. J. Atmos. Ocean. Technol. 2007, 24, 2029–2047. [Google Scholar] [CrossRef] [Green Version]
- Clerbaux, N.; Dewitte, S.; Gonzalez, L.; Bertrand, C.; Nicula, B.; Ipe, A. Outgoing longwave flux estimation: Improvement of angular modelling using spectral information. Remote Sens. Environ. 2003, 85, 389–395. [Google Scholar] [CrossRef]
- Hersbach, H. The ERA5 Atmospheric Reanalysis. In AGU Fall Meeting Abstracts; American Geophysical Union: Washington, DC, USA, 2016. [Google Scholar]
- Otterman, J.; Starr, D.; Brakke, T.; Davies, R.; Jacobowitz, H.; Mehta, A.; Cheruy, F.; Prabhakara, C. Modeling zenith-angle dependence of outgoing longwave radiation: Implication for flux measurements. Remote Sens. Environ. 1997, 62, 90–100. [Google Scholar] [CrossRef]
- Loeb, N.G.; Manalo-Smith, N.; Kato, S.; Miller, W.F.; Gupta, S.K.; Minnis, P.; Wielicki, B.A. Angular distribution models for top-of-atmosphere radiative flux estimation from the Clouds and the Earth’s Radiant Energy System instrument on the Tropical Rainfall Measuring Mission satellite. Part I: Methodology. J. Appl. Meteorol. 2003, 42, 240–265. [Google Scholar] [CrossRef]
- Di Biagio, C.; Boucher, H.; Caquineau, S.; Chevaillier, S.; Cuesta, J.; Formenti, P. Variability of the infrared complex refractive index of African mineral dust: Experimental estimation and implications for radiative transfer and satellite remote sensing. Atmos. Chem. Phys. Discuss. Eur. Geosci. Union 2014, 14, 11093–11116. [Google Scholar]
- Lolli, S.; Campbell, J.R.; Lewis, J.R.; Gu, Y.; Marquis, J.W.; Chew, B.N.; Liew, S.C.; Salinas, S.V.; Welton, E.J. Daytime top-of-the-atmosphere cirrus cloud radiative forcing properties at Singapore. J. Appl. Meteorol. Climatol. 2017, 56, 1249–1257. [Google Scholar] [CrossRef] [Green Version]
- Inoue, T. A cloud type classification with NOAA 7 split-window measurements. J. Geophys. Res. Atmos. 1987, 92, 3991–4000. [Google Scholar] [CrossRef]
- Geier, E.; Green, R.; Kratz, D.; Minnis, P.; Miller, W.; Nolan, S.; Franklin, C. CERES Data Management System: Single Satellite Footprint TOA/surface Fluxes and Clouds (SSF) Collection Document; Release 2, Version 1, 212pp. and Appendixes; NASA Langley Res. Cent.: Hampton, VA, USA, 2003. Available online: http://asd-www.larc.nasa.gov/ceres/collect_guide/SSF_CG.pdf (accessed on 30 January 2020).
- Waliser, D.E.; Zhou, W. Removing satellite equatorial crossing time biases from the OLR and HRC datasets. J. Clim. 1997, 10, 2125–2146. [Google Scholar] [CrossRef]
- Doelling, D.R.; Loeb, N.G.; Keyes, D.F.; Nordeen, M.L.; Morstad, D.; Nguyen, C.; Wielicki, B.A.; Young, D.F.; Sun, M. Geostationary enhanced temporal interpolation for CERES flux products. J. Atmos. Ocean. Technol. 2013, 30, 1072–1090. [Google Scholar] [CrossRef]
- Knapp, K.R.; Ansari, S.; Bain, C.L.; Bourassa, M.A.; Dickinson, M.J.; Funk, C.; Helms, C.N.; Hennon, C.C.; Holmes, C.D.; Huffman, G.J.; et al. Globally gridded satellite observations for climate studies. Bull. Am. Meteorol. Soc. 2011, 92, 893–907. [Google Scholar] [CrossRef]
- Schreck, C.J.; Lee, H.T.; Knapp, K.R. HIRS outgoing longwave radiation—Daily climate data record: Application toward identifying tropical subseasonal variability. Remote Sens. 2018, 10, 1325. [Google Scholar] [CrossRef] [Green Version]
- Hogan, R.J.; Bozzo, A. A flexible and efficient radiation scheme for the ECMWF model. J. Adv. Model. Earth Syst. 2018, 10, 1990–2008. [Google Scholar] [CrossRef] [Green Version]
- GCOS. Systematic Observation Requirements for Satellite-Based Products for Climate (2011 Update): Supplemental Details to the Satellite-Based Component of the “Implementation Plan for the Global Observing System for Climate in Support of the UNFCCC”. Reference Document GCOS-154, WMO. 2011. Available online: www.wmo.int (accessed on 30 January 2020).











| Release | Period Covered | Variables |
|---|---|---|
| CLARA-A1 [3] | 1982–2009 | Cloud products: fractional cloud cover, cloud top level, |
| cloud optical thickness, cloud effective radius, cloud phase, | ||
| liquid and ice water path, joint cloud histogram. | ||
| Radiation products: solar surface irradiance, surface albedo, | ||
| surface net short/longwave, surface downwelling/outgoing | ||
| longwave, surface radiation budget, cloud radiative effect. | ||
| CLARA-A2 [4] | 1982–2015 | idem as for CLARA-A1. |
| CLARA-A3 | 1979–2020 | idem as for CLARA-A1/A2, complemented by: |
| * (Surface) black sky and white sky albedo, | ||
| * (Top-of-atmosphere) Reflected Solar Flux (RSF), | ||
| * (Top-of-atmosphere) Outgoing Longwave Radiation (OLR). |
| Statistic | Channels | 5th Percentile | Mean | 95th Percentile |
|---|---|---|---|---|
| Wm−2 | Wm−2 | Wm−2 | ||
| RMS error | 2 channels | 2.85 | 4.86 | 6.85 |
| 1 channel | 3.22 | 5.99 | 8.60 | |
| Bias | 2 channels | −1.13 | −0.11 | +0.83 |
| 1 channel | −1.41 | −0.06 | +1.27 |
| Mean OLR (AVHRR) | Mean OLR (CERES | Bias | RMS Error | Factor | ||
|---|---|---|---|---|---|---|
| Wm−2 | SSF) Wm−2 | Wm−2 | Wm−2 | |||
| NOAA-17 with | 2ch | 216.14 | 215.89 | +0.35 | 4.57 | 0.9982 |
| CERES Terra | 1ch | 215.64 | −0.25 | 5.60 | 1.0011 | |
| NOAA-18 with | 2ch | 220.95 | 220.98 | −0.03 | 4.88 | 1.0002 |
| CERES Aqua | 1ch | 221.10 | +0.12 | 6.01 | 0.9996 | |
| NOAA-19 with | 2ch | 220.36 | 221.13 | −0.77 | 4.78 | 1.0038 |
| CERES Aqua | 1ch | 221.12 | −0.01 | 6.06 | 1.0001 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clerbaux, N.; Akkermans, T.; Baudrez, E.; Velazquez Blazquez, A.; Moutier, W.; Moreels, J.; Aebi, C. The Climate Monitoring SAF Outgoing Longwave Radiation from AVHRR. Remote Sens. 2020, 12, 929. https://doi.org/10.3390/rs12060929
Clerbaux N, Akkermans T, Baudrez E, Velazquez Blazquez A, Moutier W, Moreels J, Aebi C. The Climate Monitoring SAF Outgoing Longwave Radiation from AVHRR. Remote Sensing. 2020; 12(6):929. https://doi.org/10.3390/rs12060929
Chicago/Turabian StyleClerbaux, Nicolas, Tom Akkermans, Edward Baudrez, Almudena Velazquez Blazquez, William Moutier, Johan Moreels, and Christine Aebi. 2020. "The Climate Monitoring SAF Outgoing Longwave Radiation from AVHRR" Remote Sensing 12, no. 6: 929. https://doi.org/10.3390/rs12060929
APA StyleClerbaux, N., Akkermans, T., Baudrez, E., Velazquez Blazquez, A., Moutier, W., Moreels, J., & Aebi, C. (2020). The Climate Monitoring SAF Outgoing Longwave Radiation from AVHRR. Remote Sensing, 12(6), 929. https://doi.org/10.3390/rs12060929