Improving the Spatial Prediction of Soil Organic Carbon Content in Two Contrasting Climatic Regions by Stacking Machine Learning Models and Rescanning Covariate Space
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Data Collection and Soil Sample Analysis
2.3. Covariates Used for the Development of ML Models
2.4. Covariate Selection
- The covariate space is extended by adding randomly permuted existing covariates (pC) in order to remove their correlation with SOC content,
- A RF prediction using the extended covariate space (i.e., covariates and permuted covariates) is performed to predict SOC content at six standard depths,
- The Z-score, which is an indicator of the importance of all covariates, is computed,
- The maximum Z-score (MZSA) among the pC’s is defined,
- A hit is assigned to all covariates that scored better than MZSA,
- A two-test of equality is performed for undetermined important covariates,
- The original covariates are respectively flagged as “unimportant” or “important” if they have significant lower or higher scores than MZSA,
- All permuted covariates are removed,
- Repeating the procedure.
2.5. Stacked Generalization
2.5.1. The Individual ML Models in Level 0
2.5.2. Meta-Learning Models in Level 1
2.6. Optimizing the Hyper-Parameters of Machine Learning Models
2.7. Statistical Evaluation
3. Results and Discussion
3.1. Summary Statistics of SOC Content
3.2. Importance of Covariates
3.3. Performances of the Individual ML Models
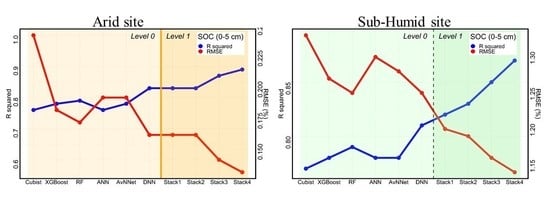
3.4. Performances of the Stacking Ensemble Models
3.5. Performances of ML Models in Two Different Climatic Regions
3.6. Spatial Distribution of SOC
4. Conclusions
- Though the differences in the ML models’ performance at both sites and at all depth intervals were rather small, DNN was identified as the most suitable individual model.
- The stacking ensemble modeling in both modes (standard mode and rescan mode) indicated the higher performance in comparison to the individual models.
- Although both terrain- and RS-based covariates were important to explain SOC contents at both sites, their explanatory power was different at both sites and at the soil depth intervals.
- The stacking models are able to explain the effect of contrasting climate on SOC content distribution. Higher content of SOC in the sub-humid site and lower content of SOC in the arid site were found, however local variation is controlled by moisture, terrain, and land use.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

| ML Models | Hyper-Parameters | Arid Site | |||||
|---|---|---|---|---|---|---|---|
| SOC 0–5 cm | SOC 5–15 cm | SOC 15–30 cm | SOC 30–65 cm | SOC 60–100 cm | SOC 100–200 cm | ||
| Cubist | committees | 3 | 3 | 7 | 5 | 4 | 3 |
| neighbors | 4 | 3 | 4 | 4 | 7 | 2 | |
| XGboost | booster | gbtree | gbtree | gbtree | gbtree | gbtree | gbtree |
| max_depth | 6 | 4 | 7 | 6 | 5 | 6 | |
| min_child_weight | 2 | 1 | 2 | 1 | 3 | 1 | |
| colsample_bytree | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | |
| subsample | 0.75 | 0.75 | 0.5 | 0.75 | 0.25 | 0.5 | |
| eta | 0.3 | 0.3 | 0.2 | 0.2 | 0.3 | 0.3 | |
| RF | Mtry | 9 | 11 | 12 | 18 | 16 | 22 |
| Ntree | 800 | 500 | 1100 | 1200 | 1800 | 2400 | |
| ANN | decay | 0.01 | 0.01 | 0.03 | 0.03 | 0.03 | 0.01 |
| size | 8 | 5 | 6 | 5 | 8 | 8 | |
| AvNNet | Repeats | 14 | 10 | 9 | 18 | 24 | 7 |
| DNN | Hidden | 4 | 4 | 6 | 5 | 6 | 8 |
| Size | 15 | 20 | 30 | 40 | 30 | 50 | |
| Network weight initialization | uniform | uniform | uniform | uniform | uniform | uniform | |
| learning rate | 0.02 | 0.05 | 0.01 | 0.03 | 0.01 | 0.02 | |
| dropout regularization | 0.7 | 0.6 | 0.3 | 0.4 | 0.4 | 0.8 | |
| ML Models | Hyper-Parameters | Sub-Humid Site | |||||
|---|---|---|---|---|---|---|---|
| SOC 0–5 cm | SOC 5–15 cm | SOC 15–30 cm | SOC 30–65 cm | SOC 60–100 cm | SOC 100–200 cm | ||
| Cubist | Committees | 4 | 5 | 3 | 8 | 7 | 5 |
| neighbors | 5 | 3 | 2 | 2 | 7 | 8 | |
| XGboost | booster | gbtree | gbtree | gbtree | gbtree | gbtree | gbtree |
| max_depth | 6 | 5 | 6 | 5 | 6 | 4 | |
| min_child_weight | 2 | 1 | 1 | 4 | 3 | 2 | |
| colsample_bytree | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | |
| subsample | 0.5 | 0.5 | 0.5 | 0.75 | 0.5 | 0.5 | |
| eta | 0.3 | 0.3 | 0.2 | 0.2 | 0.3 | 0.4 | |
| RF | Mtry | 14 | 11 | 17 | 16 | 21 | 24 |
| Ntree | 1400 | 900 | 1600 | 2100 | 2600 | 1900 | |
| ANN | decay | 0.01 | 0.01 | 0.03 | 0.03 | 0.03 | 0.01 |
| size | 8 | 5 | 6 | 5 | 8 | 8 | |
| AvNNet | Repeats | 14 | 10 | 9 | 18 | 24 | 7 |
| DNN | hidden | 4 | 4 | 6 | 5 | 6 | 8 |
| size | 50 | 20 | 40 | 40 | 50 | 60 | |
| Network weight initialization | uniform | uniform | uniform | uniform | uniform | uniform | |
| learning rate | 0.02 | 0.05 | 0.01 | 0.03 | 0.01 | 0.02 | |
| dropout regularization | 0.7 | 0.6 | 0.3 | 0.4 | 0.4 | 0.8 | |
References
- Scholten, T.; Goebes, P.; Kühn, P.; Seitz, S.; Assmann, T.; Bauhus, J.; Bruelheide, H.; Buscot, F.; Erfmeier, A.; Fischer, M. On the combined effect of soil fertility and topography on tree growth in subtropical forest ecosystems—A study from SE China. J. Plant Ecol. 2017, 10, 111–127. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A. Limited effect of organic matter on soil available water capacity. Eur. J. Soil Sci. 2018, 69, 39–47. [Google Scholar] [CrossRef] [Green Version]
- Don, A.; Schumacher, J.; Scherer-Lorenzen, M.; Scholten, T.; Schulze, E.-D. Spatial and vertical variation of soil carbon at two grassland sites—implications for measuring soil carbon stocks. Geoderma 2007, 141, 272–282. [Google Scholar] [CrossRef]
- Adhikari, K.; Owens, P.R.; Libohova, Z.; Miller, D.M.; Wills, S.A.; Nemecek, J. Assessing soil organic carbon stock of Wisconsin, USA and its fate under future land use and climate change. Sci. Total Environ. 2019, 667, 833–845. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.; Malone, B.; Wheeler, I. Digital soil mapping of carbon. Adv. Agron. 2013, 118, 1–47. [Google Scholar]
- Ajami, M.; Heidari, A.; Khormali, F.; Gorji, M.; Ayoubi, S. Environmental factors controlling soil organic carbon storage in loess soils of a subhumid region, northern Iran. Geoderma 2016, 281, 1–10. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Nabiollahi, K.; Kerry, R. Digital mapping of soil organic carbon at multiple depths using different data mining techniques in Baneh region, Iran. Geoderma 2016, 266, 98–110. [Google Scholar] [CrossRef]
- Bernhard, N.; Moskwa, L.-M.; Schmidt, K.; Oeser, R.A.; Aburto, F.; Bader, M.Y.; Baumann, K.; von Blanckenburg, F.; Boy, J.; van den Brink, L. Pedogenic and microbial interrelations to regional climate and local topography: New insights from a climate gradient (arid to humid) along the Coastal Cordillera of Chile. Catena 2018, 170, 335–355. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Jafari, A.; Bodaghabadi, M.B.; Ayoubi, S.; Taghizadeh-Mehrjardi, R.; Toomanian, N.; Kerry, R.; Xu, M. Conventional and digital soil mapping in Iran: Past, present, and future. Catena 2020, 188, 104424. [Google Scholar] [CrossRef]
- Ma, Y.; Minasny, B.; Malone, B.P.; McBratney, A.B. Pedology and digital soil mapping (DSM). Eur. J. Soil Sci. 2019, 70, 216–235. [Google Scholar] [CrossRef]
- McBratney, A.B.; Stockmann, U.; Angers, D.A.; Minasny, B.; Field, D.J. Challenges for soil organic carbon research. In Soil Carbon; Springer: Berlin, Germany, 2014; pp. 3–16. [Google Scholar]
- Minasny, B.; McBratney, A.B.; Lark, R.M. Digital soil mapping technologies for countries with sparse data infrastructures. In Digital Soil Mapping with Limited Data; Springer: Berlin, Germany, 2008; pp. 15–30. [Google Scholar]
- Behrens, T.; Scholten, T. Digital soil mapping in Germany—A review. J. Plant Nutr. Soil Sci. 2006, 169, 434–443. [Google Scholar] [CrossRef]
- McBratney, A.B.; Santos, M.M.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Grimm, R.; Behrens, T.; Märker, M.; Elsenbeer, H. Soil organic carbon concentrations and stocks on Barro Colorado Island—Digital soil mapping using Random Forests analysis. Geoderma 2008, 146, 102–113. [Google Scholar] [CrossRef]
- Moreno, R.; Irigoyen, A.I.; Monterubbianesi, M.G.; Studdert, G.A. Application of artificial neural networks to estimate soil organic carbon in a high-organic-matter Mollisol. Span. J. Soil Sci. SJSS 2017, 7, 179–200. [Google Scholar]
- Rentschler, T.; Gries, P.; Behrens, T.; Bruelheide, H.; Kühn, P.; Seitz, S.; Shi, X.; Trogisch, S.; Scholten, T.; Schmidt, K. Comparison of catchment scale 3D and 2.5 D modeling of soil organic carbon stocks in Jiangxi Province, PR China. PLoS ONE 2019, 14, e0220881. [Google Scholar] [CrossRef] [PubMed]
- Stumpf, F.; Keller, A.; Schmidt, K.; Mayr, A.; Gubler, A.; Schaepman, M. Spatio-temporal land use dynamics and soil organic carbon in Swiss agroecosystems. Agric. Ecosyst. Environ. 2018, 258, 129–142. [Google Scholar] [CrossRef]
- Wang, B.; Waters, C.; Orgill, S.; Cowie, A.; Clark, A.; Li Liu, D.; Simpson, M.; McGowen, I.; Sides, T. Estimating soil organic carbon stocks using different modeling techniques in the semi-arid rangelands of eastern Australia. Ecol. Indic. 2018, 88, 425–438. [Google Scholar] [CrossRef]
- Were, K.; Bui, D.T.; Dick, Ø.B.; Singh, B.R. A comparative assessment of support vector regression, artificial neural networks, and random forests for predicting and mapping soil organic carbon stocks across an Afromontane landscape. Ecol. Indic. 2015, 52, 394–403. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Ayoubi, S.; Jafari, A.; Tajik, S.; Finke, P. Digital mapping of soil properties using multiple machine learning in a semi-arid region, central Iran. Geoderma 2019, 338, 445–452. [Google Scholar] [CrossRef]
- Amirian-Chakan, A.; Taghizadeh-Mehrjardi, R.; Kerry, R.; Kumar, S.; Khordehbin, S.; Khanghah, S.Y. Spatial 3D distribution of soil organic carbon under different land use types. Enviro. Monit. Assess. 2017, 189, 131. [Google Scholar] [CrossRef]
- Owusu, S.; Yigini, Y.; Olmedo, G.F.; Omuto, C.T. Spatial prediction of soil organic carbon stocks in Ghana using legacy data. Geoderma 2020, 360, 114008. [Google Scholar] [CrossRef]
- Adhikari, K.; Hartemink, A.E.; Minasny, B.; Kheir, R.B.; Greve, M.B.; Greve, M.H. Digital mapping of soil organic carbon contents and stocks in Denmark. PLoS ONE 2014, 9, e105519. [Google Scholar] [CrossRef] [PubMed]
- Hinge, G.; Surampalli, R.Y.; Goyal, M.K. Prediction of soil organic carbon stock using digital mapping approach in humid India. Environ. Earth Sci. 2018, 77, 172. [Google Scholar] [CrossRef]
- Dharumarajan, S.; Kalaiselvi, B.; Suputhra, A.; Lalitha, M.; Hegde, R.; Singh, S.; Lagacherie, P. Digital soil mapping of key GlobalSoilMap properties in Northern Karnataka Plateau. Geoderma Reg. 2020, 20, e00250. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, Q.; Sun, D.; Ding, X.; Meng, F.-R. Extended model prediction of high-resolution soil organic matter over a large area using limited number of field samples. Comput. Electron. Agric. 2020, 169, 105172. [Google Scholar] [CrossRef]
- Guo, L.; Fu, P.; Shi, T.; Chen, Y.; Zhang, H.; Meng, R.; Wang, S. Mapping field-scale soil organic carbon with unmanned aircraft system-acquired time series multispectral images. Soil Tillage Res. 2020, 196, 104477. [Google Scholar] [CrossRef]
- Yang, L.; He, X.; Shen, F.; Zhou, C.; Zhu, A.-X.; Gao, B.; Chen, Z.; Li, M. Improving prediction of soil organic carbon content in croplands using phenological parameters extracted from NDVI time series data. Soil Tillage Res. 2020, 196, 104465. [Google Scholar] [CrossRef]
- Nabiollahi, K.; Eskandari, S.; Taghizadeh-Mehrjardi, R.; Kerry, R.; Triantafalis, J. Assessing soil organic carbon stocks under land-use change scenarios using random forest models. Carbon Manag. 2019, 10, 63–77. [Google Scholar] [CrossRef]
- Behrens, T.; Schmidt, K.; MacMillan, R.A.; Rossel, R.A.V. Multi-scale digital soil mapping with deep learning. Sci. Rep. 2018, 8, 15244. [Google Scholar] [CrossRef] [Green Version]
- Ng, W.; Minasny, B.; Montazerolghaem, M.; Padarian, J.; Ferguson, R.; Bailey, S.; McBratney, A.B. Convolutional neural network for simultaneous prediction of several soil properties using visible/near-infrared, mid-infrared, and their combined spectra. Geoderma 2019, 352, 251–267. [Google Scholar] [CrossRef]
- Padarian, J.; Minasny, B. Using deep learning for digital soil mapping. Soil 2019, 5, 79–89. [Google Scholar] [CrossRef] [Green Version]
- Wadoux, A.M.-C.; Padarian, J.; Minasny, B. Multi-source data integration for soil mapping using deep learning. Soil 2019, 5, 107–119. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Stacked regressions. Mach. Learn. 1996, 24, 49–64. [Google Scholar] [CrossRef] [Green Version]
- Caubet, M.; Dobarco, M.R.; Arrouays, D.; Minasny, B.; Saby, N.P. Merging country, continental and global predictions of soil texture: Lessons from ensemble modeling in france. Geoderma 2019, 337, 99–110. [Google Scholar] [CrossRef]
- Malone, B.P.; Minasny, B.; Odgers, N.P.; McBratney, A.B. Using model averaging to combine soil property rasters from legacy soil maps and from point data. Geoderma 2014, 232, 34–44. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Ribeiro, M.H.D.M.; dos Santos Coelho, L. Ensemble approach based on bagging, boosting and stacking for short-term prediction in agribusiness time series. Appl. Soft Comput. 2020, 86, 105837. [Google Scholar] [CrossRef]
- Tajik, S.; Ayoubi, S.; Zeraatpisheh, M. Digital mapping of soil organic carbon using ensemble learning model in Mollisols of Hyrcanian forests, northern Iran. Geoderma Reg. 2020, 20, e00256. [Google Scholar] [CrossRef]
- Zhou, Y.; Xue, J.; Chen, S.; Zhou, Y.; Liang, Z.; Wang, N.; Shi, Z. Fine-Resolution Mapping of Soil Total Nitrogen across China Based on Weighted Model Averaging. Remote Sens. 2020, 12, 85. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Mulder, V.L.; Heuvelink, G.B.; Poggio, L.; Caubet, M.; Dobarco, M.R.; Walter, C.; Arrouays, D. Model averaging for mapping topsoil organic carbon in France. Geoderma 2020, 366, 114237. [Google Scholar] [CrossRef]
- Smith, D. Soil Survey Staff: Keys to Soil Taxonomy; Natural Resources Conservation Service: Washington, DC, USA, 2014.
- Taghizadeh-Mehrjardi, R.; Minasny, B.; Sarmadian, F.; Malone, B. Digital mapping of soil salinity in Ardakan region, central Iran. Geoderma 2014, 213, 15–28. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. A conditioned Latin hypercube method for sampling in the presence of ancillary information. Comput. Geosci. 2006, 32, 1378–1388. [Google Scholar] [CrossRef]
- Stumpf, F.; Schmidt, K.; Behrens, T.; Schönbrodt-Stitt, S.; Buzzo, G.; Dumperth, C.; Wadoux, A.; Xiang, W.; Scholten, T. Incorporating limited field operability and legacy soil samples in a hypercube sampling design for digital soil mapping. J. Plant Nutr. Soil Sci. 2016, 179, 499–509. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Zizala, D.; Saberioon, M.; Boruvka, L. Soil organic carbon content monitoring and mapping using airborne and Sentinel-2 spectral imaging. In Proceedings of the Sixth International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2018), Paphos, Cyprus, 26–29 March 2018; p. 1077319. [Google Scholar]
- Gholizadeh, A.; Žižala, D.; Saberioon, M.; Borůvka, L. Soil organic carbon and texture retrieving and mapping using proximal, airborne and Sentinel-2 spectral imaging. Remote Sens. Environ. 2018, 218, 89–103. [Google Scholar] [CrossRef]
- Goidts, E.; Wesemael, B.V.; Van Oost, K. Driving forces of soil organic carbon evolution at the landscape and regional scale using data from a stratified soil monitoring. Glob. Chang. Biol. 2009, 15, 2981–3000. [Google Scholar] [CrossRef]
- Roozitalab, M.H.; Toomanian, N.; Dehkordi, V.R.G.; Khormali, F. Major soils, properties, and classification. In The Soils of Iran; Springer: Berlin, Germany, 2018; pp. 93–147. [Google Scholar]
- Taghizadeh-Mehrjardi, R.; Neupane, R.; Sood, K.; Kumar, S. Artificial bee colony feature selection algorithm combined with machine learning algorithms to predict vertical and lateral distribution of soil organic matter in South Dakota, USA. Carbon Manag. 2017, 8, 277–291. [Google Scholar] [CrossRef]
- Wiesmeier, M.; Urbanski, L.; Hobley, E.; Lang, B.; von Lützow, M.; Marin-Spiotta, E.; van Wesemael, B.; Rabot, E.; Ließ, M.; Garcia-Franco, N. Soil organic carbon storage as a key function of soils-a review of drivers and indicators at various scales. Geoderma 2019, 333, 149–162. [Google Scholar] [CrossRef]
- Nelson, D.W.; Sommers, L.E. Total carbon, organic carbon, and organic matter. Methods Soil Anal. Part 3 Chem. Methods 1996, 5, 961–1010. [Google Scholar]
- Malone, B.P.; McBratney, A.; Minasny, B.; Laslett, G. Mapping continuous depth functions of soil carbon storage and available water capacity. Geoderma 2009, 154, 138–152. [Google Scholar] [CrossRef]
- Arrouays, D.; Grundy, M.G.; Hartemink, A.E.; Hempel, J.W.; Heuvelink, G.B.; Hong, S.Y.; Lagacherie, P.; Lelyk, G.; McBratney, A.B.; McKenzie, N.J. GlobalSoilMap: Toward a fine-resolution global grid of soil properties. In Advances in Agronomy; Elsevier: Amsterdam, The Netherlands, 2014; Volume 125, pp. 93–134. [Google Scholar]
- Xiong, X.; Grunwald, S.; Myers, D.B.; Ross, C.W.; Harris, W.G.; Comerford, N.B. Interaction effects of climate and land use/land cover change on soil organic carbon sequestration. Sci. Total Environ. 2014, 493, 974–982. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L. The shuttle radar topography mission. Rev. Geophys. 2007, 45, 1–33. [Google Scholar] [CrossRef] [Green Version]
- Conrad, O.; Olaya, V. SAGA-GIS module library documentation (v2. 2.3). Module Valley Depth. Available online: http://www.saga-gis.org/saga_tool_doc/2.2.3/index.html (accessed on 22 January 2019).
- Wulder, M.A.; White, J.C.; Loveland, T.R.; Woodcock, C.E.; Belward, A.S.; Cohen, W.B.; Fosnight, E.A.; Shaw, J.; Masek, J.G.; Roy, D.P. The global Landsat archive: Status, consolidation, and direction. Remote Sens. Environ. 2016, 185, 271–283. [Google Scholar] [CrossRef] [Green Version]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Fongaro, C.; Demattê, J.; Rizzo, R.; Lucas Safanelli, J.; Mendes, W.; Dotto, A.; Vicente, L.; Franceschini, M.; Ustin, S. Improvement of clay and sand quantification based on a novel approach with a focus on multispectral satellite images. Remote Sens. 2018, 10, 1555. [Google Scholar] [CrossRef] [Green Version]
- Poggio, L.; Lassauce, A.; Gimona, A. Modeling the extent of northern peat soil and its uncertainty with Sentinel: Scotland as example of highly cloudy region. Geoderma 2019, 346, 63–74. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Keskin, H.; Grunwald, S.; Harris, W.G. Digital mapping of soil carbon fractions with machine learning. Geoderma 2019, 339, 40–58. [Google Scholar] [CrossRef]
- Wang, R. Significantly improving the prediction of molecular atomization energies by an ensemble of machine learning algorithms and rescanning input space: A stacked generalization approach. J. Phys. Chem. C 2018, 122, 8868–8873. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning with continuous classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Tasmania, Australia, 16–18 November 1992; pp. 343–348. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin, Germany, 2013; Volume 26. [Google Scholar]
- Minasny, B.; McBratney, A.B. Regression rules as a tool for predicting soil properties from infrared reflectance spectroscopy. Chem. Intell. Lab. Syst. 2008, 94, 72–79. [Google Scholar] [CrossRef]
- Kuhn, M.; Weston, S.; Keefer, C.; Kuhn, M.M. Package ‘Cubist’. Available online: https://cran.r-project.org/web/packages/Cubist/index.html (accessed on 22 January 2019).
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and regression trees. Wadsworth Int. Group 1984, 37, 237–251. [Google Scholar]
- Behrens, T.; Schmidt, K.; Zhu, A.-X.; Scholten, T. The ConMap approach for terrain-based digital soil mapping. Eur. J. Soil Sci. 2010, 61, 133–143. [Google Scholar] [CrossRef]
- Hounkpatin, K.O.; Schmidt, K.; Stumpf, F.; Forkuor, G.; Behrens, T.; Scholten, T.; Amelung, W.; Welp, G. Predicting reference soil groups using legacy data: A data pruning and Random Forest approach for tropical environment (Dano catchment, Burkina Faso). Sci. Rep. 2018, 8, 9959. [Google Scholar] [CrossRef] [PubMed]
- Wiesmeier, M.; Barthold, F.; Blank, B.; Kögel-Knabner, I. Digital mapping of soil organic matter stocks using Random Forest modeling in a semi-arid steppe ecosystem. Plant Soil 2011, 340, 7–24. [Google Scholar] [CrossRef]
- Peters, J.; De Baets, B.; Verhoest, N.E.; Samson, R.; Degroeve, S.; De Becker, P.; Huybrechts, W. Random forests as a tool for ecohydrological distribution modeling. Ecol. Model. 2007, 207, 304–318. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y. Xgboost: Extreme Gradient Boosting. R Package Version 0.4-2. Available online: https://github.com/dmlc/xgboost (accessed on 22 January 2019).
- Venables, B.; Ripley, B. VR: Bundle of MASS, class, nnet, spatial. R package version 7.2-42. Available online: http://CRAN.R-project.org/package=VR (accessed on 22 January 2019).
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Meyer, H.; Kühnlein, M.; Appelhans, T.; Nauss, T. Comparison of four machine learning algorithms for their applicability in satellite-based optical rainfall retrievals. Atmos. Res. 2016, 169, 424–433. [Google Scholar] [CrossRef]
- Baker, L.; Ellison, D. Optimisation of pedotransfer functions using an artificial neural network ensemble method. Geoderma 2008, 144, 212–224. [Google Scholar] [CrossRef]
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Shen, C. A transdisciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Suthaharan, S. Big data analytics: Machine learning and Bayesian learning perspectives—What is done? What is not? Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1283. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Zhai, J.; Zang, L.; Zhou, Z. Ensemble dropout extreme learning machine via fuzzy integral for data classification. Neurocomputing 2018, 275, 1043–1052. [Google Scholar] [CrossRef]
- Candel, A.; Parmar, V.; LeDell, E.; Arora, A. Deep Learning with H2O; H2O. AI Inc.: Mountain View, CA, USA, 2016. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Sotw. 2008, 33, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.J.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 28, 779–784. [Google Scholar]
- Dimitriadou, E.; Hornik, K.; Leisch, F.; Meyer, D.; Weingessel, A.; Leisch, M.F. The e1071 Package. Misc Functions of Department of Statistics (e1071), TU Wien, Vienna, Austria. R Package Version 1.5-18. Available online: https://CRAN.R-project.org/package=e1071 (accessed on 22 January 2019).
- Bischl, B.; Lang, M.; Kotthoff, L.; Schiffner, J.; Richter, J.; Studerus, E.; Casalicchio, G.; Jones, Z.M. mlr: Machine learning in R. J. Mach. Learn. Res. 2016, 17, 5938–5942. [Google Scholar]
- Valavi, R.; Elith, J.; Lahoz-Monfort, J.J.; Guillera-Arroita, G. blockCV: An R package for generating spatially or environmentally separated folds for k-fold cross-validation of species distribution models. Methods Ecol. Evol. 2019, 10, 225–232. [Google Scholar] [CrossRef] [Green Version]
- Khaledian, Y.; Miller, B.A. Selecting appropriate machine learning methods for digital soil mapping. Appl. Math. Model. 2019, 81, 401–418. [Google Scholar] [CrossRef]
- Nawar, S.; Mouazen, A.M. Predictive performance of mobile vis-near infrared spectroscopy for key soil properties at different geographical scales by using spiking and data mining techniques. Catena 2017, 151, 118–129. [Google Scholar] [CrossRef] [Green Version]
- Jafari, M.; Chahouki, M.Z.; Tavili, A.; Azarnivand, H.; Amiri, G.Z. Effective environmental factors in the distribution of vegetation types in Poshtkouh rangelands of Yazd Province (Iran). J. Arid Environ. 2004, 56, 627–641. [Google Scholar] [CrossRef]
- Goebes, P.; Schmidt, K.; Seitz, S.; Both, S.; Bruelheide, H.; Erfmeier, A.; Scholten, T.; Kühn, P. The strength of soil-plant interactions under forest is related to a Critical Soil Depth. Sci. Rep. 2019, 9, 8635. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Waters, C.; Orgill, S.; Gray, J.; Cowie, A.; Clark, A.; Li Liu, D. High resolution mapping of soil organic carbon stocks using remote sensing variables in the semi-arid rangelands of eastern Australia. Sci. Total Environ. 2018, 630, 367–378. [Google Scholar] [CrossRef]
- Vaudour, E.; Gomez, C.; Fouad, Y.; Lagacherie, P. Sentinel-2 image capacities to predict common topsoil properties of temperate and Mediterranean agroecosystems. Remote Sens. Environ. 2019, 223, 21–33. [Google Scholar] [CrossRef]
- Tziachris, P.; Aschonitis, V.; Chatzistathis, T.; Papadopoulou, M. Assessment of spatial hybrid methods for predicting soil organic matter using DEM derivatives and soil parameters. Catena 2019, 174, 206–216. [Google Scholar] [CrossRef]
- Hengl, T.; Leenaars, J.G.; Shepherd, K.D.; Walsh, M.G.; Heuvelink, G.B.; Mamo, T.; Tilahun, H.; Berkhout, E.; Cooper, M.; Fegraus, E. Soil nutrient maps of Sub-Saharan Africa: Assessment of soil nutrient content at 250 m spatial resolution using machine learning. Nutr. Cycl. Agroecosyst. 2017, 109, 77–102. [Google Scholar] [CrossRef] [Green Version]
- Ramcharan, A.; Hengl, T.; Nauman, T.; Brungard, C.; Waltman, S.; Wills, S.; Thompson, J. Soil property and class maps of the conterminous United States at 100-meter spatial resolution. Soil Sci. Soc. Am. J. 2018, 82, 186–201. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Liang, Z.; Webster, R.; Zhang, G.; Zhou, Y.; Teng, H.; Hu, B.; Arrouays, D.; Shi, Z. A high-resolution map of soil pH in China made by hybrid modeling of sparse soil data and environmental covariates and its implications for pollution. Sci. Total Environ. 2019, 655, 273–283. [Google Scholar] [CrossRef] [PubMed]
- Hengl, T.; de Jesus, J.M.; Heuvelink, G.B.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shangguan, W.; Hengl, T.; de Jesus, J.M.; Yuan, H.; Dai, Y. Mapping the global depth to bedrock for land surface modeling. J. Adv. Model. Earth Syst. 2017, 9, 65–88. [Google Scholar] [CrossRef]
- Saeedimoghaddam, M.; Stepinski, T.F. Automatic extraction of road intersection points from USGS historical map series using deep convolutional neural networks. Int. J. Geogr. Inf. Sci. 2019, 1–22. [Google Scholar] [CrossRef]
- Padarian, J.; Minasny, B.; McBratney, A.B. Using deep learning to predict soil properties from regional spectral data. Geoderma Regional 2019, 16, e00198. [Google Scholar] [CrossRef]
- Somarathna, P.D.; Minasny, B.; Malone, B.P. More data or a better model? Figuring out what matters most for the spatial prediction of soil carbon. Soil Sci. Soc. Am. J. 2017, 81, 1413–1426. [Google Scholar] [CrossRef]
- Molnar, C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable; Lean Publishing: Victoria, BC, Canada, 2018. [Google Scholar]
- Elith, J.; Ferrier, S.; Huettmann, F.; Leathwick, J. The evaluation strip: A new and robust method for plotting predicted responses from species distribution models. Ecol. Model. 2005, 186, 280–289. [Google Scholar] [CrossRef]
- Laub, M.; Blagodatsky, S.; Lang, R.; Yang, X.; Cadisch, G. A mixed model for landscape soil organic carbon prediction across continuous profile depth in the mountainous subtropics. Geoderma 2018, 330, 177–192. [Google Scholar] [CrossRef]
- Mishra, U.; Lal, R.; Slater, B.; Calhoun, F.; Liu, D.; Van Meirvenne, M. Predicting soil organic carbon stock using profile depth distribution functions and ordinary kriging. Soil Sci. Soc. Am. J. 2009, 73, 614–621. [Google Scholar] [CrossRef] [Green Version]
- Vasques, G.; Grunwald, S.; Comerford, N.; Sickman, J. Regional modeling of soil carbon at multiple depths within a subtropical watershed. Geoderma 2010, 156, 326–336. [Google Scholar] [CrossRef]








| Site Names | Area (km2) | Soil Types | Climate Conditions | Precipitation (mm/year) | Elevation (m) | Samples (no.) |
|---|---|---|---|---|---|---|
| Arid site | 720 | Solonchaks, Gypsisols and Regosols | Arid | 75 | 944–1944 | 154 |
| Sub-Humid site | 3000 | Kastanozems, Cambisols and Chernozems | Sub-Humid | 1200 | –26–700 | 99 |
| No. | Definition | Abbreviation |
|---|---|---|
| Terrain-based covariates | ||
| 1 | Elevation | Elev |
| 2 | Wetness Index | WI |
| 3 | Catchments area | Ca.Area |
| 4 | Catchment Slope | Ca.Slop |
| 5 | Multi-resolution Valley Bottom Flatness Index | MrVBF |
| 6 | Valley Depth | Vally.D |
| 7 | Plane Curvature | Pl.Cur |
| 8 | Profile Curvature | Pr.Cur |
| 9 | General Curvature | Ge.Cur |
| 10 | Total Insolation | To.In |
| Remote Sensing-based covariates | ||
| 11 | Blue band of Landsat-8 (0.482 µm) | B2.L |
| 12 | Green band of Landsat-8 (0.561 µm) | B3.L |
| 13 | Red band of Landsat-8 (0.654 µm) | B4.L |
| 14 | Near infrared band of Landsat-8 (0.864 µm) | B5.L |
| 15 | Shortwave Infrared-1 band of Landsat-8 (1.608 µm) | B6.L |
| 16 | Shortwave Infrared-2 band of Landsat-8 (2.200 µm) | B7.L |
| 17 | Blue band of Sentinel-2 (0.490 µm) | B2.S |
| 18 | Green band of Sentinel-2 (0.560 µm) | B3.S |
| 19 | Red band of Sentinel-2 (0.665 µm) | B4.S |
| 20 | Vegetation Red Edge of Sentinel-2 (0.705 µm) | B5.S |
| 21 | Vegetation Red Edge of Sentinel-2 (0.740 µm) | B6.S |
| 22 | Vegetation Red Edge of Sentinel-2 (0.783 µm) | B7.S |
| 23 | Near infrared band of Sentinel-2 (0.842 µm) | B8.S |
| 24 | Vegetation Red Edge of Sentinel-2 (0.865 µm) | B8a.S |
| 25 | Shortwave IR-1 band of Sentinel-2 (1.610 µm) | B11.S |
| 26 | Shortwave IR-2 band of Sentinel-2 (2.190 µm) | B12.S |
| 27 | Normalized difference vegetation index (Landsat-8 based) | NDVI.L |
| 28 | Normalized difference vegetation index (Sentinel-2 based) | NDVI.S |
| ML Models | Hyper-Parameters | Definition | Defined Parameters |
|---|---|---|---|
| Cubist | committees | the number of model trees | 1–100 |
| neighbors | the number of nearest neighbors | 0–9 | |
| XGboost | booster | the type of model | gbtree |
| max_depth | the depth of tree | 3–10 | |
| min_child_weight | the minimum sum of weights of all observations | 0–5 | |
| colsample_bytree | the number of variables supplied to a tree | 0.5–1 | |
| subsample | the number of samples supplied to a tree | 0.5–1 | |
| eta | learning rate | 0.01–0.5 | |
| RF | Mtry | the number of input variables | 1–30 |
| Ntree | the number of trees | 100–3000 | |
| ANN | decay | learning rate | 0.001–0.05 |
| size | the number of neurons in hidden layer | 1–10 | |
| AvNNet | Repeats | the number of MLP with different random number seeds | 3–20 |
| DNN | hidden | the number of hidden layers | 2–10 |
| size | the number of neurons in hidden layer | 15–200 | |
| network weight initialization | the initialized weight of networks | uniform/he_normal | |
| learning rate | that controls adjusting the weights of the network | 0.001–0.05 | |
| dropout regularization | the amount of the neurons that are randomly dropped | 0.2–0.8 | |
| SVM | Kernel type | the kernel function | RBF |
| C | the penalty parameter | 0.01–100 | |
| the bandwidth parameter | 0.01–100 | ||
| Lasso | lambda | the shrinkage parameter | 1–150 |
| Soil Depth | SOC (%) | ||||||
|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Lower | Upper | SD | CV | |
| Arid site | |||||||
| 0–5 cm | 0.03 | 2.34 | 0.33 | 0.26 | 0.39 | 0.42 | 128.59 |
| 5–15 cm | 0.04 | 2.21 | 0.31 | 0.25 | 0.37 | 0.39 | 124.56 |
| 15–30 cm | 0.06 | 1.69 | 0.27 | 0.23 | 0.32 | 0.30 | 110.24 |
| 30–60 cm | 0.02 | 1.11 | 0.21 | 0.19 | 0.24 | 0.17 | 77.28 |
| 60–100 cm | 0.01 | 0.75 | 0.18 | 0.16 | 0.19 | 0.11 | 60.39 |
| 100–200 cm | 0.01 | 1.00 | 0.18 | 0.16 | 0.20 | 0.14 | 78.20 |
| Sub-Humid site | |||||||
| 0–5 cm | 1.36 | 9.93 | 4.09 | 3.79 | 4.38 | 1.52 | 37.15 |
| 5–15 cm | 1.28 | 9.51 | 3.68 | 3.41 | 3.95 | 1.39 | 37.89 |
| 15–30 cm | 0.68 | 8.01 | 2.59 | 2.34 | 2.85 | 1.30 | 50.27 |
| 30–60 cm | 0.41 | 5.65 | 1.55 | 1.35 | 1.75 | 1.03 | 66.26 |
| 60–100 cm | 0.07 | 5.65 | 1.46 | 1.24 | 1.69 | 1.15 | 78.21 |
| 100–200 cm | 0.07 | 5.65 | 1.47 | 1.24 | 1.69 | 1.15 | 78.66 |
| Models | R2 | RMSE | RPIQ | R2 | RMSE | RPIQ | R2 | RMSE | RPIQ |
|---|---|---|---|---|---|---|---|---|---|
| 0–5 cm | 5–15 cm | 15–30 cm | |||||||
| Cubist | 0.76 | 0.25 | 0.84 | 0.63 | 0.24 | 0.75 | 0.63 | 0.20 | 0.67 |
| XGBoost | 0.79 | 0.20 | 1.12 | 0.71 | 0.19 | 1.02 | 0.69 | 0.17 | 0.85 |
| RF | 0.80 | 0.19 | 1.18 | 0.80 | 0.19 | 1.02 | 0.72 | 0.17 | 0.85 |
| ANN | 0.75 | 0.19 | 1.05 | 0.67 | 0.19 | 0.89 | 0.65 | 0.16 | 0.78 |
| AvNNet | 0.78 | 0.20 | 1.06 | 0.69 | 0.18 | 1.01 | 0.66 | 0.17 | 0.79 |
| DNN | 0.83 | 0.17 | 1.25 | 0.80 | 0.18 | 1.07 | 0.75 | 0.16 | 0.90 |
| Stack1 | 0.83 | 0.17 | 1.25 | 0.78 | 0.18 | 1.07 | 0.74 | 0.15 | 0.92 |
| Stack2 | 0.83 | 0.17 | 1.25 | 0.81 | 0.17 | 1.09 | 0.75 | 0.14 | 0.94 |
| Stack3 | 0.86 | 0.14 | 1.30 | 0.82 | 0.13 | 1.18 | 0.77 | 0.11 | 1.07 |
| Stack4 | 0.90 | 0.14 | 1.37 | 0.85 | 0.13 | 1.20 | 0.78 | 0.10 | 1.11 |
| 30–60 cm | 60–100 cm | 100–200 cm | |||||||
| Cubist | 0.49 | 0.14 | 0.92 | 0.29 | 0.13 | 0.90 | 0.17 | 0.16 | 0.78 |
| XGBoost | 0.56 | 0.14 | 1.00 | 0.33 | 0.13 | 0.99 | 0.26 | 0.16 | 0.84 |
| RF | 0.57 | 0.14 | 1.00 | 0.35 | 0.13 | 0.99 | 0.29 | 0.16 | 0.84 |
| ANN | 0.50 | 0.13 | 0.91 | 0.29 | 0.11 | 0.97 | 0.22 | 0.15 | 0.77 |
| AvNNet | 0.53 | 0.14 | 0.92 | 0.31 | 0.12 | 0.98 | 0.24 | 0.15 | 0.83 |
| DNN | 0.64 | 0.13 | 1.08 | 0.40 | 0.13 | 0.99 | 0.39 | 0.14 | 0.90 |
| Stack1 | 0.63 | 0.11 | 1.13 | 0.41 | 0.12 | 0.99 | 0.40 | 0.13 | 0.94 |
| Stack2 | 0.62 | 0.11 | 1.12 | 0.38 | 0.11 | 1.02 | 0.39 | 0.13 | 0.94 |
| Stack3 | 0.67 | 0.10 | 1.20 | 0.43 | 0.09 | 1.15 | 0.42 | 0.11 | 0.98 |
| Stack4 | 0.72 | 0.09 | 1.29 | 0.46 | 0.08 | 1.19 | 0.44 | 0.10 | 1.06 |
| Models | R2 | RMSE | RPIQ | R2 | RMSE | RPIQ | R2 | RMSE | RPIQ |
|---|---|---|---|---|---|---|---|---|---|
| 0–5 cm | 5–15 cm | 15–30 cm | |||||||
| Cubist | 0.78 | 1.35 | 2.00 | 0.76 | 1.26 | 1.90 | 0.66 | 1.17 | 1.62 |
| XGBoost | 0.78 | 1.28 | 2.08 | 0.76 | 1.23 | 1.92 | 0.66 | 1.10 | 1.69 |
| RF | 0.78 | 1.25 | 2.11 | 0.76 | 1.18 | 1.98 | 0.66 | 1.06 | 1.73 |
| ANN | 0.78 | 1.31 | 2.04 | 0.76 | 1.25 | 1.89 | 0.65 | 1.13 | 1.65 |
| AvNNet | 0.79 | 1.30 | 2.08 | 0.77 | 1.24 | 1.93 | 0.67 | 1.12 | 1.69 |
| DNN | 0.81 | 1.26 | 2.12 | 0.79 | 1.17 | 2.02 | 0.69 | 1.05 | 1.78 |
| Stack1 | 0.83 | 1.21 | 2.16 | 0.82 | 1.17 | 2.05 | 0.73 | 1.06 | 1.78 |
| Stack2 | 0.83 | 1.20 | 2.19 | 0.82 | 1.16 | 2.04 | 0.74 | 1.03 | 1.79 |
| Stack3 | 0.84 | 1.16 | 2.25 | 0.85 | 1.13 | 2.06 | 0.74 | 1.01 | 1.81 |
| Stack4 | 0.87 | 1.15 | 2.29 | 0.86 | 1.12 | 2.10 | 0.78 | 1.01 | 1.83 |
| 30–60 cm | 60–100 cm | 100–200 cm | |||||||
| Cubist | 0.52 | 0.99 | 1.46 | 0.32 | 1.19 | 1.07 | 0.23 | 1.22 | 1.11 |
| XGBoost | 0.61 | 0.95 | 1.49 | 0.36 | 1.12 | 1.12 | 0.27 | 1.15 | 1.16 |
| RF | 0.61 | 0.92 | 1.51 | 0.38 | 1.08 | 1.14 | 0.26 | 1.14 | 1.15 |
| ANN | 0.57 | 0.97 | 1.46 | 0.33 | 1.16 | 1.08 | 0.24 | 1.18 | 1.13 |
| AvNNet | 0.62 | 0.96 | 1.50 | 0.36 | 1.15 | 1.11 | 0.28 | 1.16 | 1.17 |
| DNN | 0.66 | 0.93 | 1.52 | 0.54 | 1.09 | 1.15 | 0.44 | 1.08 | 1.24 |
| Stack1 | 0.72 | 0.91 | 1.57 | 0.55 | 1.06 | 1.20 | 0.47 | 1.04 | 1.29 |
| Stack2 | 0.70 | 0.89 | 1.58 | 0.54 | 1.06 | 1.18 | 0.49 | 1.02 | 1.29 |
| Stack3 | 0.71 | 0.86 | 1.59 | 0.60 | 1.00 | 1.22 | 0.51 | 0.97 | 1.34 |
| Stack4 | 0.74 | 0.85 | 1.61 | 0.60 | 0.97 | 1.27 | 0.54 | 0.97 | 1.36 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taghizadeh-Mehrjardi, R.; Schmidt, K.; Amirian-Chakan, A.; Rentschler, T.; Zeraatpisheh, M.; Sarmadian, F.; Valavi, R.; Davatgar, N.; Behrens, T.; Scholten, T. Improving the Spatial Prediction of Soil Organic Carbon Content in Two Contrasting Climatic Regions by Stacking Machine Learning Models and Rescanning Covariate Space. Remote Sens. 2020, 12, 1095. https://doi.org/10.3390/rs12071095
Taghizadeh-Mehrjardi R, Schmidt K, Amirian-Chakan A, Rentschler T, Zeraatpisheh M, Sarmadian F, Valavi R, Davatgar N, Behrens T, Scholten T. Improving the Spatial Prediction of Soil Organic Carbon Content in Two Contrasting Climatic Regions by Stacking Machine Learning Models and Rescanning Covariate Space. Remote Sensing. 2020; 12(7):1095. https://doi.org/10.3390/rs12071095
Chicago/Turabian StyleTaghizadeh-Mehrjardi, Ruhollah, Karsten Schmidt, Alireza Amirian-Chakan, Tobias Rentschler, Mojtaba Zeraatpisheh, Fereydoon Sarmadian, Roozbeh Valavi, Naser Davatgar, Thorsten Behrens, and Thomas Scholten. 2020. "Improving the Spatial Prediction of Soil Organic Carbon Content in Two Contrasting Climatic Regions by Stacking Machine Learning Models and Rescanning Covariate Space" Remote Sensing 12, no. 7: 1095. https://doi.org/10.3390/rs12071095
APA StyleTaghizadeh-Mehrjardi, R., Schmidt, K., Amirian-Chakan, A., Rentschler, T., Zeraatpisheh, M., Sarmadian, F., Valavi, R., Davatgar, N., Behrens, T., & Scholten, T. (2020). Improving the Spatial Prediction of Soil Organic Carbon Content in Two Contrasting Climatic Regions by Stacking Machine Learning Models and Rescanning Covariate Space. Remote Sensing, 12(7), 1095. https://doi.org/10.3390/rs12071095