Drop Size Distribution Variability in Central Argentina during RELAMPAGO-CACTI
Abstract
:1. Introduction
2. Materials and Methods
3. Results
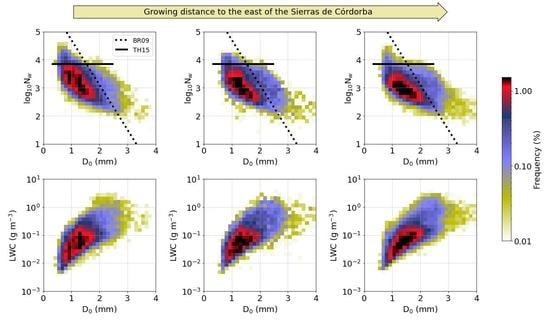
3.1. Characterization of the DSD during RELAMPAGO-CACTI
3.2. Case Studies
3.2.1. Case 1: 26 January 2019
3.2.2. Case 2: 17 January 2019
3.2.3. Case 3: 4 March 2019
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chandrasekar, V.; Gorgucci, E.; Scarchilli, G. Optimization of Multiparameter Radar Estimates of Rainfall. J. Appl. Meteorol. Climatol. 1993, 32, 1288–1293. [Google Scholar] [CrossRef] [Green Version]
- Rosenfeld, D.; Wolff, D.B.; Atlas, D. General Probability-matched Relations between Radar Reflectivity and Rain Rate. J. Appl. Meteorol. 1993, 32, 50–72. [Google Scholar] [CrossRef] [Green Version]
- Giangrande, S.E.; Ryzhkov, A.V. Estimation of Rainfall Based on the Results of Polarimetric Echo Classification. J. Appl. Meteorol. Climatol. 2008, 47, 2445–2462. [Google Scholar] [CrossRef]
- You, C.H.; Kang, M.Y.; Lee, D.I.; Uyeda, H. Rainfall estimation by S-band polarimetric radar in Korea. Part I: Preprocessing and preliminary results. Meteorol. Appl. 2014, 21, 975–983. [Google Scholar] [CrossRef]
- Meyers, M.P.; Walko, R.L.; Harrington, J.Y.; Cotton, W.R. New RAMS cloud microphysics parameterization. Part II: The two-moment scheme. Atmos. Res. 1997, 45, 3–39. [Google Scholar] [CrossRef] [Green Version]
- Saleeby, S.M.; Cotton, W.R. A Large-Droplet Mode and Prognostic Number Concentration of Cloud Droplets in the Colorado State University Regional Atmospheric Modeling System (RAMS). Part I: Module Descriptions and Supercell Test Simulations. J. Appl. Meteorol. 2004, 43, 182–195. [Google Scholar] [CrossRef] [Green Version]
- Milbrandt, J.A.; Yau, M.K. A Multimoment Bulk Microphysics Parameterization. Part I: Analysis of the Role of the Spectral Shape Parameter. J. Atmos. Sci. 2005, 62, 3051–3064. [Google Scholar] [CrossRef] [Green Version]
- Rosenfeld, D.; Ulbrich, C.W. Cloud Microphysical Properties, Processes, and Rainfall Estimation Opportunities. In Radar and Atmospheric Science: A Collection of Essays in Honor of David Atlas; Wakimoto, R.M., Srivastava, R., Eds.; American Meteorological Society: Boston, MA, USA, 2003; pp. 237–258. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.L.; Schoenhuber, M. Raindrop Size Distribution in Different Climatic Regimes from Disdrometer and Dual-Polarized Radar Analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
- Bringi, V.N.; Williams, C.R.; Thurai, M.; May, P.T. Using Dual-Polarized Radar and Dual-Frequency Profiler for DSD Characterization: A Case Study from Darwin, Australia. J. Atmos. Ocean. Technol. 2009, 26, 2107–2122. [Google Scholar] [CrossRef]
- Thompson, E.J.; Rutledge, S.A.; Dolan, B.; Thurai, M. Drop Size Distributions and Radar Observations of Convective and Stratiform Rain over the Equatorial Indian and West Pacific Oceans. J. Atmos. Sci. 2015, 72, 4091–4125. [Google Scholar] [CrossRef]
- Dolan, B.; Fuchs, B.; Rutledge, S.A.; Barnes, E.A.; Thompson, E.J. Primary Modes of Global Drop Size Distributions. J. Atmos. Sci. 2018, 75, 1453–1476. [Google Scholar] [CrossRef]
- Ulbrich, C.W.; Atlas, D. Microphysics of Raindrop Size Spectra: Tropical Continental and Maritime Storms. J. Appl. Meteorol. Climatol. 2007, 46, 1777–1791. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N.; May, P.T. CPOL Radar-Derived Drop Size Distribution Statistics of Stratiform and Convective Rain for Two Regimes in Darwin, Australia. J. Atmos. Ocean. Technol. 2010, 27, 932–942. [Google Scholar] [CrossRef]
- Jaffrain, J.; Berne, A. Experimental Quantification of the Sampling Uncertainty Associated with Measurements from PARSIVEL Disdrometers. J. Hydrometeorol. 2011, 12, 352–370. [Google Scholar] [CrossRef]
- Friedrich, K.; Higgins, S.; Masters, F.J.; Lopez, C.R. Articulating and Stationary PARSIVEL Disdrometer Measurements in Conditions with Strong Winds and Heavy Rainfall. J. Atmos. Ocean. Technol. 2013, 30, 2063–2080. [Google Scholar] [CrossRef]
- Zwiebel, J.; Van Baelen, J.; Anquetin, S.; Pointin, Y.; Boudevillain, B. Impacts of orography and rain intensity on rainfall structure. The case of the HyMeX IOP7a event. Q. J. R. Meteorol. Soc. 2016, 142, 310–319. [Google Scholar] [CrossRef]
- Murata, F.; Terao, T.; Chakravarty, K.; Syiemlieh, H.J.; Cajee, L. Characteristics of Orographic Rain Drop-Size Distribution at Cherrapunji, Northeast India. Atmosphere 2020, 11, 777. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y.; He, H.; Xie, Y.; Zeng, Q. Comparison of Raindrop Size Distributions in a Midlatitude Continental Squall Line during Different Stages as Measured by Parsivel over East China. J. Appl. Meteorol. Climatol. 2017, 56, 2097–2111. [Google Scholar] [CrossRef]
- Wen, J.; Zhao, K.; Huang, H.; Zhou, B.; Yang, Z.; Chen, G.; Wang, M.; Wen, L.; Dai, H.; Xu, L.; et al. Evolution of microphysical structure of a subtropical squall line observed by a polarimetric radar and a disdrometer during OPACC in Eastern China. J. Geophys. Res. Atmos. 2017, 122, 8033–8050. [Google Scholar] [CrossRef]
- Chen, B.; Yang, J.; Pu, J. Statistical Characteristics of Raindrop Size Distribution in the Meiyu Season Observed in Eastern China. J. Meteorol. Soc. Jpn. Ser. 2013, 91, 215–227. [Google Scholar] [CrossRef] [Green Version]
- Zipser, E.J.; Cecil, D.J.; Liu, C.; Nesbitt, S.W.; Yorty, D.P. Where Are the Most Intense Thunderstorms on Earth? Bull. Am. Meteorol. Soc. 2006, 87, 1057–1072. [Google Scholar] [CrossRef] [Green Version]
- Mezher, R.N.; Doyle, M.; Barros, V. Climatology of hail in Argentina. Atmos. Res. 2012, 114–115, 70–82. [Google Scholar] [CrossRef]
- Matsudo, C.; Salio, P. Severe weather reports and proximity to deep convection over Northern Argentina. Atmos. Res. 2011, 100, 523–537. [Google Scholar] [CrossRef]
- Rasmussen, K.L.; Zuluaga, M.D.; Houze, R.A., Jr. Severe convection and lightning in subtropical South America. Geophys. Res. Lett. 2014, 41, 7359–7366. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Gutierrez, R.; Soderholm, J.S.; Nesbitt, S.W.; Maldonado, P.; Luna, L.M.; Marquis, J.; Bowley, K.A.; Imaz, M.A.; Salio, P. Gargantuan Hail in Argentina. Bull. Am. Meteorol. Soc. 2020, 101, E1241–E1258. [Google Scholar] [CrossRef] [Green Version]
- Albrecht, R.I.; Goodman, S.J.; Buechler, D.E.; Blakeslee, R.J.; Christian, H.J. Where Are the Lightning Hotspots on Earth? Bull. Am. Meteorol. Soc. 2016, 97, 2051–2068. [Google Scholar] [CrossRef]
- Peterson, M.J.; Lang, T.J.; Bruning, E.C.; Albrecht, R.; Blakeslee, R.J.; Lyons, W.A.; Pédeboy, S.; Rison, W.; Zhang, Y.; Brunet, M.; et al. New World Meteorological Organization Certified Megaflash Lightning Extremes for Flash Distance (709 km) and Duration (16.73 s) Recorded From Space. Geophys. Res. Lett. 2020, 47, e2020GL088888. [Google Scholar] [CrossRef]
- Altinger de Schwarzkopf, M.L.; Rosso, L.C. Severe Storms and Tornadoes in Argentina. In Proceedings of the 12th Conference on Severe Local Storms, American Meteorological Society, San Antonio, TX, USA, 12–15 January 1982. [Google Scholar]
- Dias, M.A.F.S. An Increase in the Number of Tornado Reports in Brazil. Weather. Clim. Soc. 2011, 3, 209–217. [Google Scholar] [CrossRef]
- Mulholland, J.P.; Nesbitt, S.W.; Trapp, R.J.; Rasmussen, K.L.; Salio, P.V. Convective Storm Life Cycle and Environments near the Sierras de Córdoba, Argentina. Mon. Weather. Rev. 2018, 146, 2541–2557. [Google Scholar] [CrossRef]
- Cancelada, M.; Salio, P.; Vila, D.; Nesbitt, S.W.; Vidal, L. Backward Adaptive Brightness Temperature Threshold Technique (BAB3T): A Methodology to Determine Extreme Convective Initiation Regions Using Satellite Infrared Imagery. Remote. Sens. 2020, 12, 337. [Google Scholar] [CrossRef] [Green Version]
- Nesbitt, S.W.; Salio, P.V.; Ávila, E.; Bitzer, P.; Carey, L.; Chandrasekar, V.; Deierling, W.; Dominguez, F.; Dillon, M.E.; Garcia, C.M.; et al. A storm safari in Subtropical South America: Proyecto RELAMPAGO. Bull. Am. Meteorol. Soc. 2021, 1–64. [Google Scholar] [CrossRef]
- Varble, A.C.; Nesbitt, S.W.; Salio, P.; Hardin, J.C.; Bharadwaj, N.; Borque, P.; DeMott, P.J.; Feng, Z.; Hill, T.C.J.; Marquis, J.N.; et al. Utilizing a Storm-Generating Hotspot to Study Convective Cloud Transitions: The CACTI Experiment. Bull. Am. Meteorol. Soc. 2021, 1–67. [Google Scholar] [CrossRef]
- Löffler-Mang, M.; Joss, J. An Optical Disdrometer for Measuring Size and Velocity of Hydrometeors. J. Atmos. Ocean. Technol. 2000, 17, 130–139. [Google Scholar] [CrossRef]
- Löffler-Mang, M.; Blahak, U. Estimation of the Equivalent Radar Reflectivity Factor from Measured Snow Size Spectra. J. Appl. Meteorol. 2001, 40, 843–849. [Google Scholar] [CrossRef]
- Tokay, A.; Wolff, D.B.; Petersen, W.A. Evaluation of the New Version of the Laser-Optical Disdrometer, OTT Parsivel2. J. Atmos. Ocean. Technol. 2014, 31, 1276–1288. [Google Scholar] [CrossRef]
- Yuter, S.E.; Kingsmill, D.E.; Nance, L.B.; Löffler-Mang, M. Observations of Precipitation Size and Fall Speed Characteristics within Coexisting Rain and Wet Snow. J. Appl. Meteorol. Climatol. 2006, 45, 1450–1464. [Google Scholar] [CrossRef] [Green Version]
- Tokay, A.; Kruger, A.; Krajewski, W.F. Comparison of Drop Size Distribution Measurements by Impact and Optical Disdrometers. J. Appl. Meteorol. 2001, 40, 2083–2097. [Google Scholar] [CrossRef]
- Kruger, A.; Krajewski, W.F. Two-Dimensional Video Disdrometer: A Description. J. Atmos. Ocean. Technol. 2002, 19, 602–617. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N. Drop Axis Ratios from a 2D Video Disdrometer. J. Atmos. Ocean. Technol. 2005, 22, 966–978. [Google Scholar] [CrossRef]
- Tokay, A.; Petersen, W.A.; Gatlin, P.; Wingo, M. Comparison of Raindrop Size Distribution Measurements by Collocated Disdrometers. J. Atmos. Ocean. Technol. 2013, 30, 1672–1690. [Google Scholar] [CrossRef]
- Gunn, R.; Kinzer, G.D. The Terminal Velocity of Fall for Water Droplets in Stagnant Air. J. Meteorol. 1949, 6, 243–248. [Google Scholar] [CrossRef] [Green Version]
- Foote, G.B.; Toit, P.S.D. Terminal Velocity of Raindrops Aloft. J. Appl. Meteorol. Climatol. 1969, 8, 249–253. [Google Scholar] [CrossRef] [Green Version]
- Smith, P.L.; Liu, Z.; Joss, J. A Study of Sampling-Variability Effects in Raindrop Size Observations. J. Appl. Meteorol. 1993, 32, 1259–1269. [Google Scholar] [CrossRef] [Green Version]
- Smith, P.L. Sampling Issues in Estimating Radar Variables from Disdrometer Data. J. Atmos. Ocean. Technol. 2016, 33, 2305–2313. [Google Scholar] [CrossRef]
- Petty, G.W.; Huang, W. The Modified Gamma Size Distribution Applied to Inhomogeneous and Nonspherical Particles: Key Relationships and Conversions. J. Atmos. Sci. 2011, 68, 1460–1473. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M.K. The Distribution of Raindrops with Size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Junge, C.E.; Robinson, E.; Ludwig, F.L. A Study of Aerosols in Pacific Air Masses. J. Appl. Meteorol. 1969, 8, 340–347. [Google Scholar] [CrossRef] [Green Version]
- Ulbrich, C.W. Natural Variations in the Analytical Form of the Raindrop Size Distribution. J. Clim. Appl. Meteorol. 1983, 22, 1764–1775. [Google Scholar] [CrossRef] [Green Version]
- Willis, P.T. Functional Fits to Some Observed Drop Size Distributions and Parameterization of Rain. J. Atmos. Sci. 1984, 41, 1648–1661. [Google Scholar] [CrossRef] [Green Version]
- Testud, J.; Oury, S.; Black, R.A.; Amayenc, P.; Dou, X. The Concept of “Normalized” Distribution to Describe Raindrop Spectra: A Tool for Cloud Physics and Cloud Remote Sensing. J. Appl. Meteorol. 2001, 40, 1118–1140. [Google Scholar] [CrossRef]
- Hardin, J.; Guy, N. Available online: https://zenodo.org/record/9991 (accessed on 1 October 2019).
- Thurai, M.; Gatlin, P.; Bringi, V.N.; Petersen, W.; Kennedy, P.; Notaroš, B.; Carey, L. Toward Completing the Raindrop Size Spectrum: Case Studies Involving 2D-Video Disdrometer, Droplet Spectrometer, and Polarimetric Radar Measurements. J. Appl. Meteorol. Climatol. 2017, 56, 877–896. [Google Scholar] [CrossRef]
- Giangrande, S.E.; Luke, E.P.; Kollias, P. Characterization of Vertical Velocity and Drop Size Distribution Parameters in Widespread Precipitation at ARM Facilities. J. Appl. Meteorol. Climatol. 2012, 51, 380–391. [Google Scholar] [CrossRef] [Green Version]
- Saulo, A.; Nicolini, M.; Chou, S. Model characterization of the South American low-level flow during the 1997–1998 spring–summer season. Clim. Dyn. 2000, 16, 867–881. [Google Scholar] [CrossRef]
- Nicolini, M.; Saulo, A.; Torres, J.; Salio, P. Enhanced precipitation over Southeastern South America related to strong low-level jet events during austral warm season. Meteorol. Spec. Issue S. Am. Monsoon Syst. 2002, 27, 59–69. [Google Scholar]
- Salio, P.; Nicolini, M.; Zipser, E.J. Mesoscale Convective Systems over Southeastern South America and Their Relationship with the South American Low-Level Jet. Mon. Weather. Rev. 2007, 135, 1290–1309. [Google Scholar] [CrossRef] [Green Version]
- Helmus, J.; Collis, S. The Python ARM Radar Toolkit (Py-ART), a Library for Working with Weather Radar Data in the Python Programming Language. J. Open Res. Softw. 2016. [Google Scholar] [CrossRef] [Green Version]










| Id. | Project | Disdrometer | Latitude (°) | Longitude (°) | Height AMSL (m) | Starting Date | Ending Date | Sampling Time (min) | Time between Samples (min) | No. of Observations * | Region |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 001 | NSF-RELAMPAGO | OTT Parsivel 2 | −31.331 | −63.641 | 253 | 25-05-2018 | 12-03-2019 | 1 | 1 | 3905 | B |
| 003 | NSF-RELAMPAGO | OTT Parsivel 2 | −31.428 | −62.133 | 111 | 16-07-2018 | 03-05-2019 | 1 | 1 | 5647 | C |
| 004 | NSF-RELAMPAGO | OTT Parsivel 2 | −31.392 | −60.911 | 25 | 25-07-2018 | 04-05-2019 | 1 | 1 | 7186 | C |
| 005 | NSF-RELAMPAGO | OTT Parsivel 2 | −32.806 | −61.435 | 96 | 26-05-2018 | 08-05-2019 | 1 | 1 | 7458 | C |
| 007 | NSF-RELAMPAGO | OTT Parsivel 2 | −32.716 | −62.075 | 112 | 25-05-2018 | 09-05-2019 | 1 | 1 | 6705 | C |
| 008 | NSF-RELAMPAGO | OTT Parsivel 2 | −32.804 | −62.960 | 147 | 22-05-2018 | 28-03-2019 | 1 | 1 | 4423 | C |
| 010 | NSF-RELAMPAGO | OTT Parsivel 2 | −33.156 | −62.823 | 121 | 25-05-2018 | 20-03-2019 | 1 | 1 | 4692 | C |
| 013 | NSF-RELAMPAGO | OTT Parsivel 2 | −32.967 | −64.652 | 1111 | 29-05-2018 | 13-03-2019 | 1 | 1 | 7500 | A |
| 014 | NSF-RELAMPAGO | OTT Parsivel 2 | −32.472 | −64.395 | 631 | 26-05-2018 | 05-05-2019 | 1 | 1 | 7938 | A |
| 015 | NSF-RELAMPAGO | OTT Parsivel 2 | −31.668 | −63.882 | 334 | 25-05-2018 | 11-03-2019 | 1 | 1 | 4711 | B |
| APU | NASA-GPM | OTT Parsivel 2 | −31.438 | −64.194 | 432 | 06-12-2018 | 09-02-2019 | 1 | 1 | 2210 | A |
| CCT | DOE-CACTI | OTT Parsivel 2 | −32.126 | −64.728 | 1142 | 01-10-2018 | 27-04-2019 | 1 | 1 | 9720 | A |
| FDC | SINARAME | OTT Parsivel 1 | −31.521 | −64.465 | 705 | 06-01-2019 | 31-05-2019 | 1 | 10 | 300 | A |
| Mean | Mode | Standard Dev. | Minimum | Maximum | 5th Percentile | 95th Percentile | ||
|---|---|---|---|---|---|---|---|---|
| A | 1.55 | 1.30 | 0.61 | 0.51 | 7.29 | 0.81 | 2.61 | |
| B | 1.69 | 1.39 | 0.61 | 0.65 | 5.24 | 0.92 | 2.86 | |
| C | 1.79 | 1.61 | 0.65 | 0.60 | 6.90 | 0.97 | 2.96 | |
| A | 1.40 | 1.29 | 0.57 | 0.44 | 9.88 | 0.73 | 2.41 | |
| B | 1.54 | 1.24 | 0.57 | 0.50 | 6.80 | 0.84 | 2.60 | |
| C | 1.62 | 1.27 | 0.60 | 0.54 | 8.82 | 0.88 | 2.65 | |
| A | 2.78 | 2.83 | 1.29 | 0.71 | 13.39 | 1.22 | 4.89 | |
| B | 3.01 | 2.83 | 1.33 | 0.84 | 11.33 | 1.42 | 5.66 | |
| C | 3.21 | 2.83 | 1.39 | 0.84 | 13.39 | 1.42 | 5.66 | |
| log | A | 3.19 | 3.07 | 0.45 | 0.60 | 4.67 | 2.47 | 3.89 |
| B | 3.09 | 3.21 | 0.42 | 0.85 | 4.34 | 2.44 | 3.77 | |
| C | 3.02 | 2.92 | 0.40 | 0.94 | 4.54 | 2.41 | 3.67 | |
| A | 6.17 | 2.32 | 3.76 | −0.66 | 15.00 | 1.22 | 13.44 | |
| B | 6.30 | 2.87 | 3.81 | −0.42 | 15.00 | 1.37 | 13.54 | |
| C | 5.58 | 2.47 | 3.50 | −0.48 | 15.00 | 1.33 | 12.84 | |
| Mean | Mode | Standard Dev. | Minimum | Maximum | Percentile 5 | Percentile 95 | ||
| LWC | A | 0.14 | 0.02 | 0.24 | 0.00 | 4.97 | 0.01 | 0.49 |
| B | 0.17 | 0.03 | 0.27 | 0.00 | 3.59 | 0.02 | 0.67 | |
| C | 0.19 | 0.03 | 0.33 | 0.01 | 5.57 | 0.02 | 0.78 | |
| R | A | 3.00 | 0.34 | 6.17 | 0.05 | 119.46 | 0.17 | 11.58 |
| B | 3.83 | 0.38 | 6.84 | 0.05 | 97.99 | 0.24 | 16.45 | |
| C | 4.44 | 0.40 | 8.74 | 0.05 | 147.34 | 0.26 | 20.03 |
| Amb. | Group 1: Convective Precipitation | Group 2: Stratiform Precipitation | Group 3: Weak, Shallow Convection | Group 4: Heavy Stratiform Precipitation | Group 5: Low-Latitude Warm Rain | Group 6: Mixed-Phase Precipitation | |
|---|---|---|---|---|---|---|---|
| ALL | 64% | 4% | 6% | 0% | 18% | 0% | 9% |
| A | 70% | 3% | 8% | 0% | 13% | 0% | 6% |
| B | 64% | 5% | 5% | 0% | 17% | 0% | 9% |
| C | 59% | 5% | 4% | 0% | 21% | 0% | 11% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casanovas, C.; Salio, P.; Galligani, V.; Dolan, B.; Nesbitt, S.W. Drop Size Distribution Variability in Central Argentina during RELAMPAGO-CACTI. Remote Sens. 2021, 13, 2026. https://doi.org/10.3390/rs13112026
Casanovas C, Salio P, Galligani V, Dolan B, Nesbitt SW. Drop Size Distribution Variability in Central Argentina during RELAMPAGO-CACTI. Remote Sensing. 2021; 13(11):2026. https://doi.org/10.3390/rs13112026
Chicago/Turabian StyleCasanovas, Candela, Paola Salio, Victoria Galligani, Brenda Dolan, and Stephen W. Nesbitt. 2021. "Drop Size Distribution Variability in Central Argentina during RELAMPAGO-CACTI" Remote Sensing 13, no. 11: 2026. https://doi.org/10.3390/rs13112026
APA StyleCasanovas, C., Salio, P., Galligani, V., Dolan, B., & Nesbitt, S. W. (2021). Drop Size Distribution Variability in Central Argentina during RELAMPAGO-CACTI. Remote Sensing, 13(11), 2026. https://doi.org/10.3390/rs13112026