New Gridded Product for the Total Columnar Atmospheric Water Vapor over Ocean Surface Constructed from Microwave Radiometer Satellite Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Satellite Remote Sensing Data
2.1.2. Water Vapor Background
2.1.3. Radiosonde Data
2.2. Methods
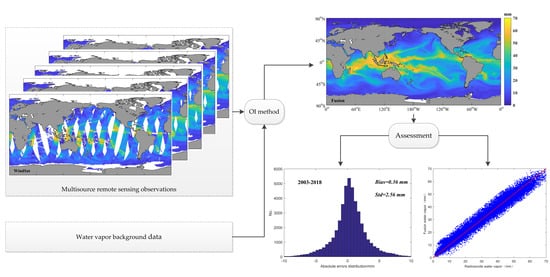
2.2.1. Water Vapor Remote Sensing Product Fusion Algorithm
2.2.2. Validation Method
3. Results
3.1. Remote Sensing Fusion Product
3.2. Precision Validation of Fusion Products Over the Past 16 Years
4. Discussion
5. Conclusions
- (1)
- Over the past 16 years, the RMSE and SD of satellite-derived atmospheric water vapor fusion products in the global ocean combined with radiosonde data are generally better than 3 mm. The Bias shows a positive deviation and is generally smaller than 0.6 mm. MAD is generally better than 2 mm, and R is stronger than 0.98. The errors of remotely sensed water vapor are normally distributed and slightly skewed to positive values from 2003 to 2018.
- (2)
- The possibility of replacing AMSR-E data with AMSR2 and HY-2A microwave radiometer data was studied after the data service of AMSR-E ceased. The findings showed that the fusion products obtained by combining AMSR2 and HY-2A microwave radiometer data show higher accuracy compared with the water vapor fusion products using AMSR-E data, based on the Bias, SD, and RMSE results. Thus, AMSR2 and HY-2A microwave radiometer data can be used to replace AMSR-E data.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sherwood, S.C.; Roca, R.; Weckwerth, T.M.; Andronova, N.G. Tropospheric water vapor, convection, and climate. Rev. Geophys. 2010, 48, 2500–2522. [Google Scholar] [CrossRef] [Green Version]
- Held, I.M.; Soden, B.J. Water vapor feedback and global warming. Annu. Rev. Energy Environ. 2000, 25, 441–475. [Google Scholar] [CrossRef] [Green Version]
- Soden, B.J.; Wetherald, R.T.; Stenchikov, G.L.; Robock, A. Global cooling after the eruption of Mount Pinatubo: A test of climate feedback by water vapor. Science 2002, 296, 727–730. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Z.; Li, M.; Zhong, W.; Wong, M.S. An approach to evaluate the absolute accuracy of WVR water vapor measurements inferred from multiple water vapor techniques. J. Geodyn. 2013, 72, 86–94. [Google Scholar] [CrossRef]
- Miloshevich, L.M.; Vömel, H.; Whiteman, D.N.; Lesht, B.M.; Schmidlin, F.J.; Russo, F. Absolute accuracy of water vapor measurements from six operational radiosonde types launched during AWEX-G and implications for AIRS validation. J. Geophys. Res. Atmos. 2006, 111, 1155–1164. [Google Scholar] [CrossRef] [Green Version]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Liu, Z.; Wong, M.S.; Nichol, J.; Chan, P.W. A multi-sensor study of water vapor from radiosonde, MODIS and AERONET: A case study of Hong Kong. Int. J. Climatol. 2013, 33, 109–120. [Google Scholar] [CrossRef] [Green Version]
- Høyer, J.L.; Karagali, I.; Dybkjær, G.; Tonboe, R. Multi sensor validation and error characteristics of Arctic satellite sea surface temperature observations. Remote Sens. Environ. 2012, 121, 335–346. [Google Scholar] [CrossRef]
- Wulfmeyer, V.; Bsenberg, J. Ground-Based Differential Absorption Lidar for Water-Vapor Profiling: Assessment of Accuracy, Resolution, and Meteorological Applications. Appl. Opt. 1998, 37, 3825–3844. [Google Scholar] [CrossRef] [PubMed]
- Cooney, J. Remote Measurements of Atmospheric Water Vapor Profiles Using the Raman Component of Laser Backscatter. J. Appl. Meteorol. 1970, 9, 182–184. [Google Scholar] [CrossRef] [Green Version]
- Huber, P.J. Projection Pursuit. Ann. Stat. 1985, 13, 435–475. [Google Scholar] [CrossRef]
- Wang, L.; Jin, W.; He, Y. Infrared and water vapor cloud image fusion using redundant dictionary sparse representation. J. Ningbo Univ. 2014, 3, 32–36. (In Chinese) [Google Scholar]
- Liu, K.; Kou, Z. Study of fusion of meteorological satellite infrared image and water vapor image. Hongwai 2013, 34, 8–15. (In Chinese) [Google Scholar]
- Wang, J.R.; Manning, W. Near concurrent MIR, SSM/T-2, and SSM/I observations over snow-covered surfaces. Remote Sens. Environ. 2003, 84, 457–470. [Google Scholar] [CrossRef]
- Hiroshima, K. Rainfall observation from Tropical Rainfall Measuring Mission (TRMM) satellite. J. Vis. 1999, 2, 93–98. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, J.; Wang, C. Objective analysis method of conventional SST data in the Northwest Pacific Ocean. I. Analysis of ten day average ship report data. Mar. Forecast. 2000, 17, 52–59. (In Chinese) [Google Scholar]
- Reynolds, R.W.; Marsico, D.C. An improved real-Time global sea surface temperature analysis. J. Clim. 1993, 6, 114–119. [Google Scholar] [CrossRef] [Green Version]
- Guan, L.; Kawamura, H. Merging satellite infrared and microwave SSTs: Methodology and evaluation of the new SST. J. Oceanogr. 2004, 60, 905–912. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Rayner, N.A.; Smith, T.M.; Wang, W. An improved in situ and satellite SST analysis for climate. J. Clim. 2002, 15, 1609–1625. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M. Improved global sea surface temperature analyses using optimum interpolation. J. Clim. 1994, 7, 929–948. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily high-resolution-blended analyses for sea surface temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Sun, W.; Wang, J.; Zhang, J.; Ma, Y.; Meng, J.; Yang, L.; Miao, J. A new global gridded sea surface temperature product constructed from infrared and microwave radiometer data using the optimum interpolation method. Acta Oceanol. Sin. 2018, 37, 41–49. [Google Scholar] [CrossRef]
- Zabolotskikh, E.; Mitnik, L.; Reul, N.; Chapron, B. New possibilities for geophysical parameter retrievals opened by GCOM-W1 AMSR2[C] Microwave Radiometry and Remote Sensing of the Environment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 161–166. [Google Scholar]
- Jiang, X.; Lin, M.; Liu, J.; Zhang, Y.; Xie, X.; Peng, H.; Zhou, W. The HY-2 satellite and its preliminary assessment. Int. J. Digit. Earth 2012, 5, 266–281. [Google Scholar] [CrossRef]
- Team of GCOM Project. GCOM-W1 “SHIZUKU” Data Users Handbook, AMSR2 Products, 1st ed.; Japan Aerospace Exploration Agency: Tokyo, Japan, 2013; pp. 4-38–4-39. [Google Scholar]
- Wenqing, T.; Yueh, S.H.; Fore, A.G.; Hayashi, A.; Lee, T.; Lagerloef, G. Uncertainty of Aquarius sea surface salinity retrieved under rainy conditions and its implication on the water cycle study. J. Geophys. Res. Oceans 2014, 119, 4821–4839. [Google Scholar]
- Martin, M.; Dash, P.; Ignatov, A.; Banzon, V.; Beggs, H.; Brasnett, B.; Gayula, J.-F.; Cummings, J.; Donlon, C.; Gentemann, C. Group for High Resolution Sea Surface temperature (GHRSST) analysis fields inter-comparisons. Part 1: A GHRSST multi-product ensemble (GMPE). Deep Sea Research Part II. Top. Stud. Oceanogr. 2012, 77, 21–30. [Google Scholar] [CrossRef]
- Kako, S.; Isobe, A.; Kubota, M. High-resolution ASCAT wind vector data set gridded by applying an optimum interpolation method to the global ocean. J. Geophys. Res. Atmos. 2011, 116, 23107. [Google Scholar] [CrossRef] [Green Version]
- Hoffmann, L.; Günther, G.; Li, D.; Stein, O.; Wu, X.; Griessbach, S.; Heng, Y.; Konopka, P.; Müller, R.; Vogel, B.; et al. From ERA-Interim to ERA5: The considerable impact of ECMWF’s next-generation reanalysis on Lagrangian transport simulations, Atmos. Chem. Phys. 2019, 19, 3097–3124. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Xu, T.; Nie, W.; Jiang, C.; Yang, Y.; Fang, Z.; Li, M.; Zhang, Z. Evaluation of Precipitable Water Vapor from Five Reanalysis Products with Ground-Based GNSS Observations. Remote Sens. 2020, 12, 1817. [Google Scholar] [CrossRef]











| Sensors | Resolution | Data Time Period Used | Spatial Coverage |
|---|---|---|---|
| AMSR-E | Daily/25 km | January 2003–October 2011 | Global ocean |
| AMSR2 | Daily/25 km | July 2012–December 2018 | Global ocean |
| WindSat | Daily/25 km | January 2003–December 2018 | Global ocean |
| SSMIS | Daily/25 km | January 2003–December 2018 | Global ocean |
| HY-2A MR | Swath/97 km | October 2011–December 2015 | Global ocean |
| Year | Data Matches | Bias (mm) | MAD (mm) | SD (mm) | RMSE (mm) | R |
|---|---|---|---|---|---|---|
| 2003 | 2365 | 0.50 | 2.07 | 2.79 | 2.84 | 0.99 |
| 2004 | 2961 | 0.52 | 1.94 | 2.60 | 2.65 | 0.99 |
| 2005 | 2916 | 0.87 | 2.04 | 2.66 | 2.80 | 0.99 |
| 2006 | 2771 | 0.99 | 2.52 | 3.17 | 3.33 | 0.98 |
| 2007 | 2616 | 0.36 | 2.24 | 3.02 | 3.04 | 0.99 |
| 2008 | 2847 | 0.48 | 2.04 | 2.78 | 2.83 | 0.98 |
| 2009 | 3036 | 0.66 | 1.80 | 2.43 | 2.53 | 0.99 |
| 2010 | 3490 | 0.43 | 1.53 | 2.11 | 2.15 | 0.99 |
| 2011 | 3098 | 0.41 | 1.84 | 2.67 | 2.70 | 0.99 |
| 2012 | 3014 | 0.24 | 1.56 | 2.15 | 2.16 | 0.99 |
| 2013 | 2969 | 0.30 | 1.72 | 2.42 | 2.44 | 0.99 |
| 2014 | 2998 | 0.57 | 1.87 | 2.52 | 2.59 | 0.98 |
| 2015 | 2870 | 0.37 | 1.96 | 2.70 | 2.73 | 0.98 |
| 2016 | 2755 | 0.30 | 1.85 | 2.60 | 2.62 | 0.99 |
| 2017 | 2520 | 0.54 | 1.78 | 2.51 | 2.57 | 0.99 |
| 2018 | 1965 | 0.66 | 1.65 | 2.27 | 2.36 | 0.99 |
| Year | Bias (mm) | MAD (mm) | SD (mm) | RMSE (mm) | R |
|---|---|---|---|---|---|
| 2016 | 0.64 | 1.94 | 2.86 | 2.93 | 0.99 |
| 2017 | 0.62 | 1.82 | 2.69 | 2.76 | 0.99 |
| 2018 | 0.87 | 1.96 | 3.17 | 3.29 | 0.99 |
| Data | Year | MAD (mm) | SD (mm) | RMSE (mm) | R |
|---|---|---|---|---|---|
| Fusion product | 2016 | 1.58 | 2.30 | 2.30 | 0.99 |
| Fusion product | 2017 | 1.69 | 3.89 | 3.89 | 0.97 |
| Fusion product | 2018 | 1.67 | 2.46 | 2.48 | 0.99 |
| RSS product | 2016 | 1.61 | 2.38 | 2.39 | 0.99 |
| RSS product | 2017 | 1.74 | 3.85 | 3.86 | 0.97 |
| RSS product | 2018 | 1.73 | 2.53 | 2.58 | 0.99 |
| Data | Bias (mm) | MAD (mm) | SD (mm) | RMSE (mm) | R |
|---|---|---|---|---|---|
| Fusion product using ERA-interim | 0.66 | 1.65 | 2.27 | 2.36 | 0.99 |
| Fusion product using ERA5 | 0.72 | 1.68 | 2.28 | 2.39 | 0.99 |
| ERA5 reanalysis | 1.08 | 2.12 | 3.44 | 3.60 | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Wang, J.; Li, Y.; Meng, J.; Zhao, Y.; Wu, P. New Gridded Product for the Total Columnar Atmospheric Water Vapor over Ocean Surface Constructed from Microwave Radiometer Satellite Data. Remote Sens. 2021, 13, 2402. https://doi.org/10.3390/rs13122402
Sun W, Wang J, Li Y, Meng J, Zhao Y, Wu P. New Gridded Product for the Total Columnar Atmospheric Water Vapor over Ocean Surface Constructed from Microwave Radiometer Satellite Data. Remote Sensing. 2021; 13(12):2402. https://doi.org/10.3390/rs13122402
Chicago/Turabian StyleSun, Weifu, Jin Wang, Yuheng Li, Junmin Meng, Yujia Zhao, and Peiqiang Wu. 2021. "New Gridded Product for the Total Columnar Atmospheric Water Vapor over Ocean Surface Constructed from Microwave Radiometer Satellite Data" Remote Sensing 13, no. 12: 2402. https://doi.org/10.3390/rs13122402
APA StyleSun, W., Wang, J., Li, Y., Meng, J., Zhao, Y., & Wu, P. (2021). New Gridded Product for the Total Columnar Atmospheric Water Vapor over Ocean Surface Constructed from Microwave Radiometer Satellite Data. Remote Sensing, 13(12), 2402. https://doi.org/10.3390/rs13122402