Influence of Wind-Induced Effects on Laser Disdrometer Measurements: Analysis and Compensation Strategies

Abstract

Nowadays, laser disdrometers constitute a very appealing tool for measuring surface precipitation properties, by virtue of their capability to estimate not only the rainfall amount and intensity, but also the number, the size and the velocity of falling drops. However, disdrometric measures are affected by various sources of error being some of them related to environmental conditions. This work presents an assessment of Thies Clima laser disdrometer performance with a focus on the relationship between wind and the accuracy of the disdrometer output products. The 10-min average rainfall rate and total rainfall accumulation obtained by the disdrometer are systematically compared with the collocated measures of a standard tipping bucket rain gauge, the FAK010AA sensor, in terms of familiar statistical scores. A total of 42 rainy events, collected in a mountainous site of Southern Italy (Montevergine observatory), are used to support our analysis. The results show that the introduction of a new adaptive filtering in the disdrometric data processing can reduce the impact of sampling errors due to strong winds and heavy rain conditions. From a quantitative perspective, the novel filtering procedure improves by 8% the precipitation estimates with respect to the standard approach widely used in the literature. A deeper examination revealed that the signature of wind speed on raw velocity-diameter spectrographs gradually emerges with the rise of wind strength, thus causing a progressive increase of the wrongly allocated hydrometeors (which reaches 70% for wind speed greater than 8 m s⁻¹). With the aid of reference rain-gauge rainfall data, we designed a second simple methodology that makes use of a correction factor to mitigate the wind-induced bias in disdrometric rainfall estimates. The resulting correction factor could be applied as an alternative to the adaptive filtering suggested by this study and may be of practical use when dealing with disdrometric data processing.

1. Introduction

Detailed and accurate knowledge about rainfall amount and its characteristics is useful in a lot of different applications and research fields. As an example, the importance of providing information about the type of particle in the managing of winter road traffic was discussed in [1]. Other applications concern the study of a relationship between soil erosion and rainfall characteristics [2] and the aerosol–precipitation interaction [3]. All the mentioned applications require a detailed microphysical description of falling hydrometeors. Nowadays, many hydrometeor measurement techniques are available. They evolved from initial manual methods, such as stain, flour pellet, oil immersion and photographic ones, into in automated devices such as disdrometers. The latter are weather sensors able to estimate the number, the size and the velocity of precipitation particles. Due to their affordable costs, low power consumption and maintenance requirements, such devices are more and more employed in both operational and research contexts. In recent years, disdrometers have been used for many hydrometeorological tasks (e.g., [4]), as well as for the evaluation of hydrometeor classification algorithms developed from dual-polarization weather radar measurements [5].

Among various type of disdrometers, those based on laser principles measure the modification of the emitted laser signal, within the small sensitive volume of detection, as the falling drops slice it. Each falling drop contributes to reducing the laser signal strength and the residence time within the sensitive volume. These two quantities are those being directly measured by the disdrometer and are used to obtain the size and fall velocity of each particle that crosses the measuring area. An alternative for the measure of drop size, velocity and number is offered by two-dimensional video disdrometers (2DVD), which are capable of recoding images of each hydrometeor passing through the sensing area. More in detail, the measurement principle of 2DVD can be described as follows. Two light planes, emitted by two internal lamps, cut across the virtual measurement area (approximately 100 cm²) and are projected onto two high-speed line-scan cameras. The drops that fall through the light planes cast a shadow that is recorded by the two cameras implanted within the instrument [6]. The light planes are divided by a calibrated distance between which the speed of a falling hydrometeor can be measured. The line scan cameras sample with a very high frequency (up to 18 microseconds), providing several line scans of each image. The 2DVD instrument has been involved in many field experiments, and its performance in rain rate and amount estimates have been recently compared in [7], using a laser disdrometer and a weighing precipitation gauge.

The accuracy of laser disdrometers, in terms of the output particles’ size vs. falling velocity spectrograph, may be influenced by several factors, such as wind and turbulence conditions, which may introduce some errors into the falling velocity measurements [8]. More specifically, whenever a vertical wind shear component of the horizontal winds is taking place and/or in the presence of turbulence, the particle’s fall speed is directly biased (i.e., it slows down or accelerates depending by the vertical wind orientation). However, even a purely horizontal wind component might alter the particle’s fall speed retrieved by the laser disdrometer. This could happen for two reasons. The first one is caused by the outer frame of the instrument, which exerts an air resistance to the external wind then produces a horizontal and a vertical small-scale airflow modification within the sensitive volume of the disdrometer [9]. The second reason is due to the drop trajectory deviation caused by an external horizontal wind. In this case, the falling particles cross the instrument sensitive volume following a slanted trajectory, the latter being a condition that the disdrometer is not able to discern with respect to the vertical path. Consequently, as a general rule, the particle residence time within the instrument sensitive volume is decreased, thus causing a higher fall speed estimation then what would be expected in calm air.

To compensate for wind effects, an alternative version of the classical optical laser didrometer was conceived in [10]. An evolution of this modified disdrometer, including a paired pulse and therefore named the paired-pulse optical disdrometer (P-POD), was then proposed in [11] and operationally used in [12,13]. Innovations brought by [10] and [11] were mainly concerned on the cylindical shape of the sensitive volume to avoid the dependence of the crossing drops by their incident angle of arrival.

Focusing on most popular and conventional devices (Thies Clima and Parsivel), the wind effects on disdrometric measurements were firstly investigated in [14] through a comparison between three differently oriented Thies Clima disdrometers. The results of this study showed that, in light winds, the orientation of the disdrometer was irrelevant, but as the wind increased in speed the instrument lost ever-higher proportions of drops. In fact, smaller drops were most susceptible to some form of masking, which prevented them from passing through the sensitive volume of the instrument, and, consequently, up to 20% of these drops remained undetected when the wind direction was from behind the body of the instrument. A comparison between a Thies Clima disdrometer and tipping-bucket rain-gauge measurements was carried out in [15]. The difference found between the two instruments did not show any relevant linear relationship with wind speed and direction, aside from a weak dependence on winds parallel to the disdrometer axis, although no information regarding the mean or maximum wind intensity was present in that paper. Measurements in windy conditions were also analyzed by comparing a stationary disdrometer (Parsivel) with an articulating disdrometer, which continuously oriented the sample area perpendicular to the wind [16,17]. Once the wind speed exceeded a critical value (10 m s⁻¹), the stationary disdrometers observed unrealistically large slow-falling drops that caused misclassification. The wind effects on the shape of drop size distribution (DSD) and the driving microphysical processes for the DSD shape evolution were investigated in [18], using the dataset from the Midlatitude Continental Convective Clouds Experiment (MC3E). This study highlighted that wind speed might impact on DSD shapes, resulting in an increase in the number of small drops and in a reduction of the number of large drops, indicating that the raindrop breakup process might govern the DSD shape evolution in such harsh conditions. In a very recent work [19], different aspects that can affect the quality of the optical disdrometer data (such as number of bits of the AD converters, sampling time, type of measurement technique, wind intensity and precipitation) have been analyzed. According to the achievements of this study, increasing wind speed values determine an underestimation in precipitation intensity estimated by the disdrometer. The wind-induced airflow near the Thies disdrometer has been recently analyzed and discussed in [9]. Starting from an ideal scenario, in which the device is free of obstacles and has no wind-protection shield, this work simulated the impact of the instrument itself on the wind field around the sensor trough computational fluid dynamics models. The results highlighted that the non-axisymmetric outer geometry of the instrument has an important effect on the airflow pattern near the sensing area, generating vertical and accelerated/decelerated velocity components. The authors found that the wind direction is the most impactful element in determining the magnitude of these perturbations: the most unfavorable (favorable) configuration is when the wind direction forms an angle of 180° (90°) with respect to the line of the sensing area.

However, wind effects are only one detrimental aspect that drives the final quality of disdrometer measures. The inaccuracies in disdrometer data may also be related to (i) an overestimation of particle size for multiple drops that simultaneously slice the sensitive volume and for this reason are detected as a single drop; (ii) drops that fall at the edge of the sensor’s sampling area (i.e., margin fallers) being, in general, wrongly sized (underestimation), although margin-faller effects can be mitigated by adopting a modified sampling area according to the particle size [20]; (iii) external structure effects, that is, the influence of surrounding structures (sensor mounting block included) that foster the breakup of drops by splashing them away with stronger acceleration, altering the natural variability of the drop size distribution.

Obviously, traditional reference rain gauges are not exempted by issues too. It is important to highlight that wind speed constitutes a serious drawback also for tipping-bucket rain gauges, as demonstrated by many studies (e.g., [21,22,23,24]). Recently, in [25], the relationships between catch efficiency, defined as the ratio between non-reference gauges (mounted above ground), reference (pit gauge) rainfall measurements and wind speed have been analyzed. The authors demonstrated that it is necessary to correct non-reference gauge records under certain conditions, to reduce wind-induced undercatch. The functional dependency of the collection efficiency on rainfall intensity was analyzed for a cylindrical gauge in [26]. A new adjustment curve, which requires only the wind speed and the measured rainfall intensity as input variables, was obtained.

Due to the just mentioned source of errors, a comparison between the data obtained from disdrometer and a traditional rain gauge is recommended in order to assess the accuracy of rain intensity and amount measurements. Many previous studies have compared different types of disdrometers to each other and have investigated the estimated precipitation parameters, whose differences can be explained by the different design and internal data-processing methods (e.g., [27,28,29,30]). However, there exists few studies focused on the assessment of disdrometer performance with respect to traditional reference gauges (e.g., [7,31,32]), and, more importantly, no post-processing method has been yet conceived to compensate for the bias introduced by wind speed in disdrometric data.

This work aims to fill this gap by proposing a new processing methodology to compensate for the detrimental wind effects that corrupt laser disdrometer measurements. To this goal, data from the Thies Clima laser disdrometer, collected between December 2019 and November 2020 in a mountainous site of Southern Italy (Montevergine Observatory), are considered. The performance of Thies disdrometers has been analyzed and discussed in terms of two essential precipitation parameters: the rainfall intensity (mm h⁻¹) and the rainfall amount (mm). The benchmark used as reference is a tipping-bucket rain gauge, the FAK010AA of MTX s.r.l., the output of which was compensated for wind effects. The corrected rain-gauge data have been compared with disdrometer measurements in three cases: (i) a “raw” disdrometric dataset (without any filtering procedure), (ii) an “ad hoc” disdrometric dataset, obtained by means of a new filtering procedure and (iii) a “literature” disdrometric dataset, obtained using the traditional filtering procedure suggested in [33]. In addition, using the data collected by the cup-anemometer operating in Montevergine Observatory, we have evaluated the impact of wind on disdrometer velocity-diameter spectrographs. With the support of this analysis and of the reference rain gauge, we have designed a correction factor to mitigate the adverse effects of wind speed in disdrometer rainfall estimates.

The quantitative analysis has been supported by some familiar statistical scores, such as the percentage error, the mean absolute error and the root mean square error.

The paper is organized as follows. Section 2 describes the device characteristics and their principles of functioning and provides a description of the collected dataset. Section 3 discusses the methodology proposed in this study to optimally process disdrometer data, as well as provide details about the criteria used to compare the data collected by the instruments. Section 4 presents the results of the comparison between the disdrometer and the rain gauge, whereas Section 5 analyzes and discusses the wind and turbulence effect on disdrometer data. In Section 6, conclusions are drawn.

2. Input Measurements

The measurement devices involved in this work are the Thies Clima disdrometer and the FAK010AA rain-gauge sensor, which are briefly described in this section together with the collected dataset.

2.1. Thies Clima Disdrometer

The Thies Clima disdrometer is a laser optical device and provides information on precipitation drop spectra and hydrometeor type (drizzle, rain, snow, hail and mixed precipitation). A laser-optical beam source produces an infrared (780 nm) parallel-beam and the optical intensity is transformed into an electrical signal by a photo diode placed on the receiver side [34]. The working principle is light extinction, and, when drops pass through the laser beam, the receiving signal is reduced according to the diameter of the hydrometeors. Velocity is determined from the residence time of crossing drops within the sensitive volume, while the diameter is calculated from the obscuration amplitude. The sampling area is 45.6 ${\mathrm{cm}}^2$, the result of a 20 mm wide and 0.75 mm thick beam. The sample rate (i.e., the rate at which the analog to digital (A/D) converter scans the optical signal) is 109 kHz. The Thies Clima stores data over one minute and groups particles into 22 and 20 classes of diameter size and fall velocity ranging from 0.125 to 9 mm and from 0 to 12 m s⁻¹, respectively. From raw device output, information about the number of hydrometeors detected for each size-velocity class has been grouped into a 22 × 20 matrix, which is called a spectrograph. In addition, rain rate, precipitation-amount and precipitation-type data, computed by Thies Clima software, are also available. To partly mitigate the turbulence and severe wind effects, a protection shield, consisting of laminations in stainless steel, has been mounted around the disdrometer.

The Thies Clima disdrometer combines affordable costs and easy deployment but has some intrinsic limits, mainly due to the hardware design and/or inadequate software corrections. These limits have been clearly highlighted by some previous studies e.g., [20,27] through comparisons with the Parsivel device. According to the findings of these works, the main difference between the Thies and Parsivel devices lies in the amount of recorded drops and in spectrograph spread, which are both higher in Thies. More specifically, in Thies, data on a significant number of drops with unexpected combination of very small size and excessive high velocities data has been observed. These anomalies are compatible with edge events [20] and can have a relevant impact on bulk variables estimates [27].

The precipitation amount and the rain rate have been derived from raw and filtered Thies spectrographs by the following equations [20,35]:

$$ND\left(D_j\right)={\displaystyle \sum }_{i=1}^{20}{N}_{ij}\left(\frac{1}{A_j∆t∆D_{j}v(D_j)}\right)$$

(1)

$$A_j=A\left(1-\frac{D_j}{2w}\right)$$

(2)

$$RR=\frac{6\pi }{{10}^4\rho }{\displaystyle \sum }_{j}v\left(D_j\right)D_j{}^{3}ND\left(D_j\right)∆D_j$$

(3)

$$P=RR∆t$$

(4)

where ND is the drop size distribution (m⁻³ mm⁻¹); D_j is the j-th diameter class (mm); N_i,j is the number of drops in the size class D_j and velocity class $v_i$; Δt is the sampling time interval (s); ΔD_j is the diameter interval for the j-th diameter class (mm); A is the sampling area of the disdrometer (45.6 cm²); w is the width of the laser beam (20 mm); RR is the rain rate (${\mathrm{mm} \mathrm{h}}^{-1}$); $\rho$ is the water density (1.0 g cm⁻³); P is the rainfall amount (mm), and v is the fall velocity (m s⁻¹). The latter has been obtained as follows: in the literature scenario, it has been determined from the theoretical terminal-velocity–diameter relationship proposed in [33], in the raw scenario from a simple power fitting of the available spectrograph and in the ad hoc scenario from a specific power fitting that will be described in detail in Section 3. It should be pointed out that the terminal velocity v used in Equation (1) is the same adopted in Equation (3), so it does not have a direct impact on the calculation of the rain rate since it cancels out in Equation (3). However, v has an indirect impact on rain-rate calculations because its behaviour drives the selection of the samples N_ij in Equation (1), thus modifying N(D) and RR accordingly. The sampling area A has been modified in A_j according to the drop size, in order to avoid measurement issues related with margin fallers [20].

2.2. FAK010AA Rain Gauge

The FAK010AA is a precipitation sensor with a collecting area of 1000 ${\mathrm{cm}}^2$. The collector is made of anodized aluminum, and the shape prevents rain from splashing in and out. An appropriate circular deflector reduces the undesired effects of the turbulence caused by wind. When the precipitation fills one of the collectors, the tipping bucket loses balance, overturns and puts the empty bucket in the collection position. The instrument reports upon the event by generating an electrical output signal. The process then repeats itself. This rain gauge has an accuracy of 2% over the entire operating range (0–300 mm h⁻¹) and a resolution of 0.2 mm. The technical specifications of the FAK010AA sensors meet the World Meteorological Organization (WMO) recommendations.

When the precipitation is solid (snow or hail), the measurement is carried out by evaluating the amount of water released by melting. However, in the period analyzed in this study, the FAK010AA was not equipped with a proper heating system, and, therefore, it was not able to provide reliable measurements of liquid equivalent for solid precipitation.

The rainfall records collected by the FAK010AA rain gauge in the considered period have been corrected for wind-induced bias using the relationship suggested in [26].

2.3. Masuring Site and Collecetd Dataset

The considered dataset includes 42 rainy events that occurred between December 2019 and November 2020 in the experimental site of the Montevergine observatory. The latter is located in the Southern Apennines (Figure 1) on the eastern hillside of the Partenio Mountains and is an historical observatory that was established in 1884 [36]. The meteorological instruments in Montevergine include an automatic weather station (AWS) that provides temperature, humidity, pressure, solar radiation and wind speed and direction; the FAK010AA rain gauge; and the Thies Clima disdrometer. All the instruments were placed on the observatory terrace (Figure 1).

Among all available events in the examined period, some of them have been discarded due to the presence of solid hydrometeors (graupel, snow and hail) that were not adequately detected by the rain gauge due to the absence of a heating system. The resulting final dataset encompasses a wide spectrum of meteorological scenarios, including different precipitation regimes (convective, stratiform and orographic), as well as different synoptic and mesoscale forcing.

Table 1. List of the selected events including average rain rate (mm h⁻¹) and total precipitation amount (mm) recorded by FAK010AA rain gauge, as well as 10-min average, maximum and minimum wind speed (m s⁻¹) measured by AWS.

Date (dd/mm/yy)	ID Number	Average Rain Rate (mm h−1)	Rainfall Amount (mm)	Average Wind Speed (m s−1)	Max Wind Speed (m s−1)	Min Wind Speed (m s−1)
09/12/2019	1	4.3	16.2	1.8	4.9	0.5
20/12/2019	2	2.5	8.1	1.9	3.6	0.5
29/12/2019	3	6.1	78.8	3.0	5.4	1.3
25/01/2020	4	1.3	1.7	0.9	1.8	0.0
26/01/2020	5	1.6	4.8	0.4	2.7	0.0
27/01/2020	6	2.1	1.4	2.7	3.6	2.2
29/01/2020	7	1.8	6.7	1.8	4.9	0.9
02/10/2020	8	1.7	3.8	0.5	1.8	0.0
02/11/2020	9	1.2	1.0	2.0	2.2	1.8
14/02/2020	10	4.4	18.9	1.4	3.6	0.5
28/02/2020	11	4.8	24.6	2.2	4.0	1.3
01/03/2020	12	4.4	8.1	2.2	3.1	1.8
02/03/2020	13	2.8	8.9	3.5	4.5	1.8
22/03/2020	14	1.3	1.3	8.5	9.8	6.7
26/03/2020	15	1.5	11.4	8.5	14.3	0.5
27/03/2020	16	2.0	9.8	1.8	4.5	0.0
20/04/2020	17	1.9	27.5	1.4	6.3	0.0
21/04/2020	18	1.5	7.2	4.2	8.5	0.5
22/04/2020	19	3.0	30.2	4.5	6.7	1.8
23/04/2020	20	1.3	2.4	8.0	9.4	6.7
28/04/2020	21	1.7	1.2	1.6	1.8	1.3
29/04/2020	22	3.3	1.1	0.7	0.9	0.5
05/03/2020	23	10.2	27.1	3.3	5.8	1.3
20/05/2020	24	2.0	8.7	3.4	5.8	0.5
21/05/2020	25	1.9	3.7	10.2	14.8	7.2
29/05/2020	26	11.4	9.7	1.4	2.2	0.5
30/05/2020	27	1.8	7.1	3.4	4.9	0.0
31/05/2020	28	4.3	7.3	1.3	3.1	0.5
01/06/2020	29	1.5	0.9	0.8	1.3	0.5
03/06/2020	30	7.2	4.8	5.9	6.7	4.5
05/06/2020	31	3.2	28.0	2.7	4.5	0.5
08/06/2020	32	6.9	4.0	0.7	1.3	0.0
10/06/2020	33	6.9	10.6	4.8	8.1	1.3
11/06/2020	34	2.0	5.3	2.2	5.8	0.5
16/06/2020	35	2.3	5.1	3.6	7.2	0.5
21/06/2020	36	5.0	11.7	2.3	4.9	0.5
04/07/2020	37	2.6	2.6	2.8	5.4	0.0
17/07/2020	38	2.4	7.0	2.6	6.3	0.0
18/07/2020	39	5.1	3.4	1.9	3.6	0.5
27/09/2020	40	11.3	125.2	2.9	6.3	0.9
20/11/2020	41	2.7	31.8	5.3	15.2	0.0
29/11/2020	42	1.6	14.6	6.1	13.9	1.8

provides a list of the events, including total precipitation amount and average rainfall rate recorded by the FAK010AA rain gauge, as well as average wind speed measured by the AWS. The average rain rate varies between 1.2 mm h⁻¹ (lower limit detected by rain gauge) and 11.4 mm h⁻¹, while cumulative rainfall ranges between 1 mm and 125 mm. For each event, disdrometric data, i.e., the number of hydrometeors collected for each class of velocity and diameter, are available with a resolution of 1 min. Other useful meteorological data collected by AWS, such as air temperature, relative humidity, atmospheric pressure, wind speed (average and gust) and wind direction are still available with the same temporal resolution. The FAK010AA rain gauge data, i.e., rainfall amount and average rainfall intensity, are also stored with a 1-min temporal resolution.

3. Methodology

In this section, disdrometer and rain-gauge data processing is discussed.

3.1. Disdrometric Data Filtering

In this work, three different processing levels applied to the available disdrometric dataset have been considered for the comparison with rain-gauge data. A “raw” version, which includes the unprocessed data collected by the device, and two filtered versions, defined as “literature” and “ad hoc”. The latter two are the result of two different filtering methods for velocity-diameter spectrographs acquired from the disdrometer. Both have been applied to raw disdrometric data and aim to remove or at least mitigate the impact of spurious measurements in the spectrographs. According to the “literature” method, hydrometeors whose velocity differs more than ∓50% from the theoretical terminal fall velocity [33] are removed (Figure 2a). Although the theoretical terminal fall velocity for rain drops is in generally average good agreement with experimental findings, it is derived under the assumption of still air, which is a condition not always met during precipitation events. Consequently, there could be cases, especially in the presence of turbulence and windy regimes, were the ∓50% rule is not adequate and the risk is to filter out (include) significant (not significant) parts of the spectrographs (Figure 2b).

The new “ad hoc” filtering procedure, proposed in this study can be considered an alternative to the literature approach, which is the most widely used method.

The motivation behind the “ad hoc” filtering method is to overcome the limitations caused by the still air assumption by adapting the filtering procedure to the observed spectrographs characteristics regardless any a-priori constraints related to theoretical assumptions on hydrometeor terminal velocity. In other words, the goal of the proposed filtering method is not to bring back the actual terminal velocity vs. drop diameter curve to that theoretically expected. Our filtering method indeed aims at estimating an experimental drop velocity vs. drop diameter curve more closely related to the windy environment in which the drops fall. Such obtained experimental drop velocity is not necessarily representative of the true unknown drop terminal velocity since the wind-induced errors in the disdrometer spectrographs are difficult to trace back to a precise source or to a wind configuration. For this reason, our filtering method is not exempt from errors, although the final error on the disdrometer rain rate is maintained lower than the benefit obtained by applying the proposed filtering procedure (see Section 4). After the experimental velocity curve is identified, the measured velocities inside a confidence interval are retained. This approach, as will be demonstrated in this study, can strongly mitigate the impact of some issues, such as strong wind conditions, that might distort the classical shape of the drop size distribution for rain events.

More specifically, the “ad hoc” filtering process consists of three steps. First, for each instant (one minute), raindrops with fall velocity greater or equal to 9.5 m s⁻¹ and diameter smaller or equal to 1.875 mm are deleted, and, if the number of recorded size classes is smaller than three, precipitation is considered zero. The second step consists of a weighted power fit of data, where weights are obtained as follows:

$$w_{ijk}=\frac{n_{ijk}}{m_k}$$

(5)

where n_ijk is the number of particles with fall velocity v_i and diameter D_j, and m_k is the absolute maximum value of n_ijk detected in a given k-time instant. Bins (i.e., size-velocity classes) whose velocity differs more than ∓60% with the weighted power fit, are discarded. In order to mitigate the incidence of residual anomalous raindrops (characterized, for example, by very high terminal velocity and very small diameter), a new power fitting without weights is applied to the spectrograph obtained in the previous step: only bins that are within ∓80% with power fit are accepted. As a result, a filtered “ad hoc” version of the original spectrograph that automatically adapts to various v_i vs. D_j scenarios is obtained.

Figure 3 shows two typical examples, collected on 09 December, 2019, of the disdrometric data filtering processes under light (left panels) and moderate (right panels) wind conditions, quantified by the AWS as 0.1 m s⁻¹ and 5.2 m s⁻¹, respectively.

The raw spectrograph data collected in the light-wind scenario (panel a of Figure 3) resembles the typical velocity-diameter distribution observed for rainfall events, except for some anomalous drops characterized by very low size (< 0.5 mm) and velocity between 3 and 6 m s⁻¹. The right top panel (b) presents a raw spectrograph that is strongly corrupted by the horizontal winds and that appears to diverge from the theoretical distribution for rain events. The effects of the “literature” filtering are shown in the middle panels: c, d. In a light-wind regime, the resulting spectrograph (c) is reasonably filtered by the literature approach that is able to discard the outliers present in the raw data (a). In a moderate-wind regime (b), the horizontal wind seems to have determined a shift of the velocity-diameter spectrograph towards the hydrometeor classes associated with a small diameter (<1 mm) and very high vertical speed (up to 10–12 m s⁻¹). In this situation, the literature approach (d) seems to be inadequate, since it tends to filter out most of the significant raw data, thus producing an unrealistic spectrograph. The “ad hoc” scenario (e, f) better represents the information content in the raw data and, at the same time, allows keeping out the outliers. From this example clearly emerges the more adaptive nature of the ad hoc method that has the ability to filter out the most anomalous region of the velocity-diameter spectrum and, at the same time, to retain the most-populated classes. The result is a spectrum that appears to be qualitatively in agreement with the theoretical one, although exhibiting slight differences compared to it, and the more important thing that it holds most of the information content in terms of hydrometeor numbers.

3.2. Metrics of Comparison

The following statistical performance indicators, the mean absolute error (MAE), the BIAS, the error percentage (E) and the root mean square error (RMSE) have been used to quantify the difference between the Thies Clima and the FAK010AA rain gauge:

$$MAE=\frac{{{\displaystyle \sum }}_{k=1}^n|R{R}_{di{s}_k}-R{R}_{pl{u}_k}|}{n},$$

(6)

$$BIAS=\frac{1}{n}{{\displaystyle \sum }}_{k=1}^n\left(\frac{R{R}_{pl{u}_k}}{R{R}_{di{s}_k}}\right),$$

(7)

$$E=\frac{P_{di{s}_k}-P_{pl{u}_k}}{P_{pl{u}_k}}\ast 100\%,$$

(8)

$$RMSE=\sqrt[2]{\frac{{{\displaystyle \sum }}_{k=1}^n{(R{R}_{di{s}_k}-R{R}_{pl{u}_k})}^2}{n}}$$

(9)

where $R{R}_{di{s}_k}$, $P_{di{s}_k}$ and $R{R}_{pl{u}_k}$, $P_{pl{u}_k}$ are the rain rate and rainfall amount measured at k-th time by disdrometer and rain gauge, respectively, and n is the total number of available records.

To alleviate the mismatches related to temporal misalignment between disdrometer and rain gauge measurements, which might be caused by the different measuring principles of the two devices, both data sources have been aggregated over a 10-min period. The rainfall amount is obtained as the time integral of 1-min rain intensity over the 10-min period in which each daily event in Table 1 has been undersampled. The rainfall intensity calculation follows the same criteria used for the rainfall amount except that the average is considered instead of the integral. Only 10-min records in which both instruments have detected rainfall have been taken into account. Using this strategy, a population of 954 10-min samples has contributed to the statistical analysis discussed in the next section.

4. Results

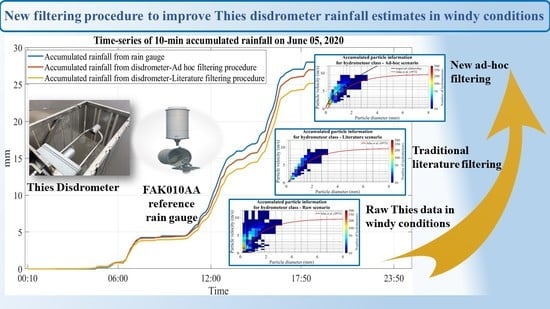
For each of the selected rainy events, a systematic comparison between 10-min precipitation intensities and rainfall amounts detected by a FAK010AA rain gauge and a Thies disdrometer has been performed. Figure 4 sketches the time-cumulative precipitation of the raw, ad hoc and literature disdrometric data as compared to the FAK010AA rain gauge. The full investigation period has been taken into account. A close inspection of this graph easily allows evaluating the benefits introduced by the new filtering procedure proposed in this study. More specifically, the ad hoc method has improved the agreement in terms of cumulated rainfall between the rain gauge and disdrometer by 14.8% with respect to the raw scenario over the full period. If we consider the classical literature approach for disdrometric data filtering, the improvement drops to 6.8% (nearly half less).

Additional and relevant evidence of the benefit of the “ad hoc” approach are also provided by Figure 5, which shows a scatter diagram between 10-min rainfall rate measurements collected by the two devices in the analyzed period for the three different scenarios considered in this work. The analysis of Figure 5a, in which raw disdrometric data are shown, reveals important discrepancies between the two devices, especially for RR values greater than 20 mm h⁻¹. Figure 5b highlights that the ad hoc filtering procedure produces a better alignment between disdrometer and rain-gauge measures. From the analysis of Figure 5c, which is referred to the literature scenario, emerge results similar to those just achieved for the ad hoc framework. However, there is an important difference, which justifies the discrepancies previously discussed in terms of E score (see also

Table 2. Rain gauge vs. disdrometer error statistical indicators of rain rate in terms of error percentage (E), mean absolute error (MAE) and the root mean square error (RMSE), as defined by Equations (8), (6) and (9), respectively. The mean and standard deviation (Std) are listed for all scenarios. These results refer to the whole dataset.

	Disdrometric Data Scenario
Statistical Indicator	Raw		Ad hoc		Literature
E	20.4%		−5.6%		−13.6%
	Mean	Std	Mean	Std	Mean	Std
MAE	1.2 mm h−1	1.1 mm h−1	1.0 mm h−1	0.6 mm h−1	1.1 mm h−1	0.6 mm h−1
RMSE	2.0 mm h−1	2.8 mm h−1	1.4 mm h−1	1.0 mm h−1	1.4 mm h−1	1.0 mm h−1

). For low rain-rate values, in fact, in the literature scenarios, there is a substantial number of records lying at the left of the reference line (means that the disdrometer underestimates the rain rate with respect to the reference rain gauge). As pointed out by the color scale, which shows the 10-min average wind speed registered by AWS, a large part of low rain rate samples is affected by moderate or strong horizontal wind. A focus on this aspect is provided in the next section.

Figure 6 presents MAE and RMSE values for each of the 42 rainy events, labeled on the x-axis of both panels through their ID number (see Table 1). More specifically, blue lines show the results obtained from raw Thies Clima data, whereas red and orange lines show those achieved from the ad hoc and literature scenarios, respectively. The impact of filtering processes determines, for both scores, a reduction of mean and standard deviation (Table 2). The results are slightly better when the ad hoc scenario is considered. The event-by-event MAE and RMSE trend sketched in Figure 6 allows to stress some evidence that emerged from the discussion of Figure 5. Focusing on the filtering scenarios, a close inspection of red (ad hoc) and orange (literature) curves reveals significant differences for the following events: 14, 15, 20, 25, 30, 33, 41 and 42. In all these cases, the MAE and RMSE scores obtained in the literature framework are worse than those achieved for the ad hoc method. In these events, an average wind speed ranging from 5.3 to 10 m s⁻¹ has been measured, as indicated by Table 1. Furthermore, it is worth noting that the blue curve strongly diverges from optimal MAE and RMSE values for events #3, 11, 23, 28, 32 and 40, wherein, according to the FAK010AA sensor, the average rain rate ranged from 4.3 to 11.3 mm h⁻¹.

5. Analysis of Wind Effects on Disdrometric Measurements

In this section, we investigate in more detail the impact of wind speed on disdrometric measurements. We have structured this analysis as follows:

• Firstly, we provide qualitative and quantitative evidence of the wind footprint on raw velocity-diameter spectrographs, by a proper matching between 1-min raw disdrometric and wind speed data. This investigation has been supported by a metric that assess the deviation of the observed spectrographs from the theoretical distribution for rainfall events as a function of different wind velocity classes, ranging from calm winds to strong breeze. Using the concept of turbulence intensity [37], we also estimate the effect of turbulence on the disdrometer spectrographs.
• Subsequently, for each wind class, we have computed the bias between 10-min rain gauge and disdrometric measurements, considering all different scenarios involved in this study (raw, ad hoc and literature). The functional dependence of the bias from wind speed has been modeled with a three-order polynomial fit.

5.1. Wind Effects Characterization

The first task of this analysis involves the 1-min disdrometer (raw data) and AWS measurements. To avoid undesired temporal mismatching that may be ascribed to a lack of synchronization between the clocks of the two devices, a careful manual inspection of available data has been performed. The latter highlighted slight temporal misalignment in some events, which have been discarded for this analysis. In order to filter out other impairments, such as double detection, that may mask or alter the wind speed effects in heavy rain conditions, we have selected only times in which the RR estimated by raw disdrometer data range between 0.1 and 2.5 mm h⁻¹ (i.e., only light rain events). Indeed, light rain is more easily influenced by moderate wind than heavy rain, and, for this reason, it is more suitable for a wind-effect investigation. The approach used to evaluate the possible impact of wind on Thies Clima velocity-diameter spectrographs starts from a classification of available data with respect to nine different wind speed thresholds (

Table 3. Classification of available data with respect to nine different wind speed thresholds with $w_{avg}$ ∈ [$w_{tr{e}_{low}}$, $w_{tr{e}_{up}}$).

Class	$\mathbf{Lower} \mathbf{Threshold} {\mathit{w}}_{\mathit{t}\mathit{r}{\mathit{e}}_{\mathit{l}\mathit{o}\mathit{w}}} \left({\mathbf{ms}}^{-1}\right)$	$\mathbf{Upper} \mathbf{Threshold} {\mathit{w}}_{\mathit{t}\mathit{r}{\mathit{e}}_{\mathit{u}\mathit{p}}} \left({\mathbf{ms}}^{-1}\right)$
1	0	0.5
2	0.5	1.5
3	1.5	3
4	3	4
5	4	5
6	5	6
7	6	8
8	8	10
9	10	15

). The Thies Clima spectrum collected in a determined 1-min interval has been associated with a certain wind class if, in that instant, the average wind speed is within the limits of that class and if the wind gust meets the following criterion, defined as:

$$w_{max}\le 0.5\ast w_{tr{e}_{up}}+w_{avg}$$

(10)

where w_max is the wind gust (defined as the maximum wind speed value observed in a 1-min interval); w_avg is the 1-min average wind speed, and $w_{tr{e}_{up}}$ is the upper threshold of a determined wind class. Both w_avg and w_max have been measured by AWS and are expressed in m s⁻¹. The criterion expressed by Equation (10) allows discarding some minutes in which the wind gust strongly departs from average wind speed. These cases are the result of very turbulent conditions and may undermine the reliability of our analysis, introducing potential biases in the wind-speed-based categorization of disdrometer spectrographs.

Subsequently, the spectrographs associated with each wind class have been aggregated through a simple sum of the number of hydrometeors detected for each velocity-diameter class. To quantify the number of drop-size classes erroneously categorized due to wind effects, we introduce a metric based on the two following indicators:

• Class ratio detection (CRD), which is defined as the ratio, computed for each wind group, between the number of classes that differ by more than ∓50% with the theoretical terminal velocity relationship found in [33] and the total number of classes detected by the disdrometer;
• Drop ratio detection (DRD), which is the actual number of drops correctly classified and has been determined as the ratio between the sum of particles inside the range ∓50% of the values imposed by the literature relationship [33] and the total number of hydrometeors detected by the disdrometer in each wind group.

Figure 7 provides graphical evidence of the results of this analysis. This figure presents the aggregated Thies Clima spectrograph for different wind speed classes, ranging from calm wind (0–0.5 m s⁻¹) to moderate strong breeze (10–15 m s⁻¹). Combinations differing by more than 50% with the theoretical fall velocity are represented in the figure with transparency. It can be easily noted that the number of anomalous velocity-diameter classes rapidly increases with increasing wind speed thresholds. The impact of wind speed results in a sort of dilatation of the Thies Clima spectrum, which is nearly centered to the theoretical distribution for rainfall events only in calm wind conditions and tends to a butterfly-like shape in the strongest wind considered. With the increasing of wind velocities thresholds, there is a rapid increase of spurious hydrometeor classes whose velocity-diameter values are not consistent with those expected for rainfall. It is interesting to highlight that, for wind speed up to 10 m s⁻¹, the anomalies in the Thies Clima spectrum grow in the region of high velocities (>3 m s⁻¹) and small diameter (<1 mm). This effect is likely the result of the natural increase in speed of small raindrops, which, as virtue of their reduced size, are easily subjected to strong departures from their theoretic terminal velocity in windy conditions. However, it should be kept in mind that this region of disdrometer spectrum may be affected by systematic errors due to the drops falling at the edge of the device’s visual field, where the accuracy in hydrometeor size and velocity estimation is poor.

For wind speed greater than 10 m s⁻¹, the spectrum appears to be dilated too in the region of low velocity (<3 m s⁻¹) and relatively higher diameter (2–3.5 mm). To explain this second effect, we guess that strong wind conditions may influence the disdrometer measure by altering the device’s ability to discriminate between each hydrometeor falling in a determined rain event. In other words, our hypothesis is that, in such circumstances, a certain number of drops that rapidly cross the field of view of the disdrometer are considered one drop by the device. This effect dilates the time employed by the particle to cross the light beam and, therefore, leads to an underestimation of the fall velocity and to a size overestimation.

Figure 8 shows the behavior of CRD (Figure 8a) and DRD (Figure 8b) indicators for increasing wind speed thresholds. According to CRD, the percentage of anomalous hydrometeor size classes goes from 43% in calm wind events to around 70% when wind speed is more than 10 m s⁻¹. Moreover, as clearly indicated by DRD index, for wind speed ranging to 0 and 0.5 m s⁻¹, almost the 70% of the hydrometeors is well-classified. This percentage dramatically drops with increasing wind speed, reaching a value below 20% for wind speed exceeding 4 m s⁻¹.

5.2. Turbulence Effect

The impact of the wind field on disdrometer data has also been investigated from the turbulence perspective. It is well known that a solid evaluation of turbulence can be performed only with a sonic anemometer, which is able to measure the fast-response wind measurements in two or three dimensions. Unfortunately, only 1-min average wind speed and direction data from three-cup anemometer are available for this study.

Therefore, to investigate the impact of the turbulence on disdrometer data, we calculated the turbulence intensity (TI), defined in [37], as:

$$TI=\frac{\sigma }{\mu }$$

(11)

where σ and $\mu$ are the standard deviation and average of the horizontal wind speed time series within a sliding time window $∆T=N \delta T$, respectively. The quantity $\delta T$ is the resolution time of the horizontal wind speed acquisitions by the three-cup anemometer, and it is set to 1 min. Consequently, N is set to 10 to have $∆T=10 \min$, which is the usual practice in the literature e.g., [37].

Figure 9 shows TI vs. the 10-min averaged wind speed for the entire analyzed dataset (black dots). A power law fitting curve is also overimposed (red). From this figure, an inverse relationship of TI and wind speed is clear, in agreement with previous studies [38,39]. For each wind speed level, we arbitrary defined high (low) turbulence regimes when TI is larger (lesser) than the 90h (10th) percentile represented in Figure 9.

The impact of the turbulence on the disdrometer is described by Figure 10 where some examples of 10-min aggregated spectrographs are shown for low (left panels a,c) and high (right panels b,d) TI conditions. The spectrographs in panels (a)–(b) and (c)–(d) are obtained under nearly the same wind speed, so the differences between the two set of panels are, with reasonable certainty, driven by turbulence effects. Indeed, comparing left and right panels, it is worth noting that, in high TI conditions, an increase of anomalous counts in the region characterized by very low diameters is registered. This result confirms that turbulence effects are more impactful on small-sized drop diameters, which follow more easily the turbulent flow [40]. The generalization of such a conclusion for the whole available dataset is investigated in terms of CRD and DRD indices, introduced in the previous section, which represent the degree of spectrograph deviation from the theoretical one. CRD = 0% and DRD = 100% indicate an optimal situation with no spectrograph deformation. To better isolate the turbulence effects, we restrict the evaluation of CRD and DRD scores to the spectrograph region of low diameters (<=1.5 mm). For small wind regimes (wind speed less than 3.0 m s⁻¹), wherein turbulence is expected to play a primary role, we found CRD = 50% and DRD = 80% for low TI cases, whereas for high TI, CRD = 58% and DRD = 62% evidenced lower spectrograph deformation for lower turbulence regimes.

Moreover, in the discussion of these results, it is important to take into account the direction of wind flow and the local installation facility, which may amplify or wear down the disdrometer sampling errors. In this respect, we have performed a further examination, testing the CRD and DRD indices for two particular wind directions (hereafter, WD1 and WD2) in high TI regimes. WD1 is within 0–180° sector (i.e., in a clockwise reference system with 0° indicating the north direction, the 0–180° sector indicates winds from the north, north-eastern, eastern, south-eastern directions) whereas WD2 is within 180–360° (i.e., winds from the south, south-western, western and north-western directions).

Due to the absence or scarcity of cases simultaneously characterized by wind speed greater than 4 m s⁻¹ and wind direction ranging from 180 to 360°, we have restricted this analysis to the first four wind classes.

Table 4. CRD and DRD index value, expressed in percentage, for two different wind direction classes, WD1 and WD2 (0–180° and 180–360°, respectively) in a high-turbulence scenario. The results are presented for the first four wind speed classes.

Wind Speed Class	CRD Index (%)		DRD Index (%)
	WD1 (0–180°)	WD2 (180–360°)	WD1 (0–180°)	WD2 (180–360°)
0–0.5 m s−1	40	38	52	81
0.5–1.5 m s−1	44	46	30	59
1.5–3.0 m s−1	55	49	16	37
3.0–4.0 m s−1	55	54	19	27

shows CRD (a) and DRD (b) indices for the two wind directions considered. It is quite clear that winds in WD1 from the north and east directions are associated with worse scores and, therefore, have a stronger impact on disdrometer spectrographs.

An explanation for such wind-direction dependence, in our environmental conditions, is likely that winds in WD1 from north-east, east and south-east are naturally forced upwards, following the eastern side of the Montevergine relief. Such an orographic upward velocity forcing is expected to have a specific impact on the disdrometer spectrographs.

In this respect, Figure 11 shows aggregated spectrographs for WD1 (Figure 11a) and WD2 (Figure 11b) for horizontal winds less than 4 m s⁻¹ conditioned to a high TI regime. As evident from this figure, the spectrograph for the WD1 sector, due to local vertical orographic forcing in a high turbulence environment, shows relevant growth in the number of particles characterized by a very small diameter (<0.4 mm) and relatively high terminal velocity than what happens for WD2. This finding highlights the importance of the orientation of the disdrometer with respect to the prevailing wind, as pointed out in [9,16], as well as the local orography of the installation site. Consequently, it would be highly recommended to have collocated wind and disdrometer measurement, as well as to accurately evaluate local orographic effects.

5.3. Wind Effects Compensation on Disdrometer Rainfall

The last part of this research has been devoted to the evaluation of wind speed impact on disdrometer rainfall estimates and its possible compensation. To pursue this goal, we have computed the bias (see Equation (7)) between the reference rain-gauge measurements and the disdrometer for each of the nine wind classes defined in Table 3. Figure 12 sketches the average bias value obtained for individual classes considering the three scenarios analyzed in this study (namely, raw, ad hoc and literature) and three different rain rate ranges: 0.1–2.5 mm h⁻¹ (blue curve in Figure 12), which is the same taken into account in the previous analysis; 2.5–10 mm h⁻¹ (red curve), which includes moderate rain rate events; and >10 mm h⁻¹ (orange curve), which represents the heavy rain events. Unfortunately, no heavy rain events are available for wind classes #1, 8 and 9.

Focusing on light-rain scenarios, in which it is reasonable to assume that sampling errors in disdrometric measurements are mainly due to wind effects, it is easy recognize that the discrepancies between the two devices abruptly grow from wind class #5 (4–5 m s⁻¹) and maximize for wind speeds between 6 and 8 m s⁻¹. For wind velocities greater than 8 m s⁻¹, a reduction of bias can be observed in ad hoc and raw scenarios. This result may be interpreted as a consequence of the appearance, in strong wind conditions, of anomalous hydrometeors characterized by the butterfly spectrograph shape, which has the property to be more symmetric, thus producing a balance between large drops vs. small velocities and small drops vs. high velocities zones. In this situation, the comparison with the reference rain gauge tends to be more unbiased (see Figure 7e,f). In other words, according to our findings, in very strong wind conditions there is a sort of “compensation effect” that tends to reduce the discrepancies with respect to rain-gauge data, especially in raw scenarios. The literature scenario seems to suffer more by the strong winds in terms of BIAS likely because of the static nature of the method.

For moderate-rain events, bias shows a gradual increase with the raising of wind velocity, reaching the highest value for wind class #7. It is straightforward noting that bias magnitude is lower than in light rain conditions. In heavy rain cases, the bias still has a slight positive trend with increasing wind speed, but it further reduces and became negligible for ad hoc and literature scenarios. As it can be expected based on the results discussed in Section 4, in a raw framework, strong rainfall events means an overestimation of rain-rate values (i.e., BIAS < 1).

Based on the results in Figure 12, we have derived a correction factor that may be useful to mitigate wind effects on disdrometer measurements. More specifically, the relationship between wind speed and BIAS score has been modeled with a Bisquare weight method, a robust regression technique that minimizes the effect of outliers. The best fit was achieved with a third-order polynomial fit. In this way, we have obtained a simple correction factor, dependent only on wind speed, which can be easily applied as a multiplier to rainfall intensity estimated by a disdrometer.

In order to explore the potential benefits introduced by this correction factor, we have applied it to the disdrometric dataset involved in this study. Among the scenarios presented in Figure 12, we have selected the one most affected by wind speed issues (literature disdrometric data with light-rain conditions). It is fair to note that the correction factor is applied to a subset of data used to derive it. This is obviously not strictly rigorous but it gives a general guidance, although optimistic, of the potentials of the method. A deep verification test is left to a future validation work. Figure 13 shows the results of this application: in particular, Figure 13a sketches the third-order polynomial fitting (blue curve) applied to the available data, whereas the right panel (Figure 13b) provides a comparison between the reference rain gauge and the corrected literature disdrometric records in terms of 10-min accumulated rainfall over the overall analyzed period.

The correction factor clearly improves the literature disdrometric measures, which exhibit a very good alignment with benchmark data provided by the FAK010AA sensor. To support this result, we have newly computed the statistical indices: as indicated by

Table 5. For each statistical indicator, the mean and standard deviation (named Std for the sake of brevity) are listed for literature disdrometric data before and after the correction for wind effects. As in Table 2, these results are referred to the whole dataset.

	Literature Disdrometric Data Scenario
Statistical Indicator	No Wind Correction		With Wind Correction
E	−13.6%		−1.8%
	Mean	Std	Mean	Std
MAE	1.1 mm h−1	0.6 mm h−1	1.0 mm h−1	0.7 mm h−1
RMSE	1.4 mm h−1	1.0 mm h−1	1.4 mm h−1	1.0 mm h−1

, a relevant improvement (13%) can be observed in the E score, whose value after wind correction is near to the optimal one. For MAE and RMSE indices, negligible or very slight improvements have been detected.

It is obvious that those achievements, although encouraging, are not sufficient for a robust assessment of the proposed correction methodology. More tests, based on independent datasets, are necessary to validate our methodology.

6. Conclusions

In this work, the performance of a Thies Clima laser-optical disdrometer has been investigated in Montevergine, a well-instrumented site of the Apennines in Southern Italy. Using a dataset consisting of 42 rainy events that occurred between December 2019 and November 2020, an extensive comparison between the disdrometer and a reference tipping-bucket rain gauge, the FAK010AA, has been performed in terms of two essential bulk variables, the rain rate and the accumulated rainfall.

The results achieved from this analysis clearly highlight that the filtering strategy employed in the processing of raw spectrographs plays a crucial role in compensating for the effects of sampling errors that can undermine disdrometer data quality. More specifically, we have tested two different filtering procedures, the one usually employed in the literature, based on the theoretical terminal velocity model for rain events introduced in [33], and a new adapting strategy. As testified by percentage error, the novel filtering approach outperforms by 8% the standard procedure in terms of accumulated rainfall over the entire analyzed period, proving to be efficient in mitigating the effects of horizontal winds. A proper matching between 1-min time resolution disdrometric and anemometric data demonstrated that wind speed has a double distortion effect on raw spectrographs: it determines a rapid growth of anomalous very fast and small particles and, for wind speed exceeding 10 m s⁻¹, an increase in slow and relative large hydrometeors. The net result of wind impact on spectrographs is a strong loss of mass when a standard filtering procedure is applied and, therefore, a relevant underestimation of rainfall amounts especially in light-rain events. This study has also proved that turbulence has a relevant effect on disdrometer data for low wind speed values (less than 3.0 m s⁻¹). The signature of turbulence on spectrographs is represented by an anomalous growth of very small hydrometeors (<0.4 mm), which results in a lowering of 18% of particles correctly located within a region close (±50%) to the theoretical line. In our test site, the impact of turbulence is emphasized when winds blow from specific directions (ranging from north-eastern to south-eastern): in these circumstances, in fact, the local orography forces an upward wind component, which contributes to distorting the spectrographs.

An alternative approach to compensate for wind errors relies on the design of a correction factor based on a systematic comparison of disdrometric records with reference to rain-gauge data. In this work, we have modeled the wind-induced bias affecting disdrometric records with a third-order polynomial fit. The latter has been applied to the available data determining a relevant improvement of rainfall estimates provided by standard literature filtering method, which exhibited a near optimal alignment to the benchmark data. It is important to highlight that this result is the fruit of an idealized scenario in which the dataset used to evaluate the performance of the correction method is the same involved for the training. In this respect, future work shall be devoted to assess the reliability of this approach through independent datasets collected in different locations and with different installation facilities.

At the same time, it should be pointed out that the findings of our study about wind effects on disdrometric spectrographs may be dependent on specific factors, such as site exposure and local wind field, and therefore, may be not generalizable without a proper tuning. In other words, the “added-value” of our work lies in the proposed methodological aspects, rather in their implementation on our specific test site.

To conclude, this work highlights that environmental conditions, and in particular the occurrence of strong winds, need to be carefully taken into account in the processing of disdrometric data for the retrieval of bulk variables. The standard procedure usually adopted to filter out spurious hydrometeors needs to be optimized and adapted in order to avoid undesired bias that may limit the reliability of these devices in both operational and research contexts. The two compensation methods proposed in this study, the ad hoc adaptive filter and the third-order polynomial factor, may be two valuable options to remove or at least mitigate the bias introduced by wind speed. The user may select one or other method or use both, depending on the specific situation and meteorological data availability.

Future research should also be dedicated to extend the comparison between rain gauges and disdrometers to winter precipitation events (i.e., snow and graupel).