Empirical Models for Spatio-Temporal Live Fuel Moisture Content Estimation in Mixed Mediterranean Vegetation Areas Using Sentinel-2 Indices and Meteorological Data
Abstract
:1. Introduction
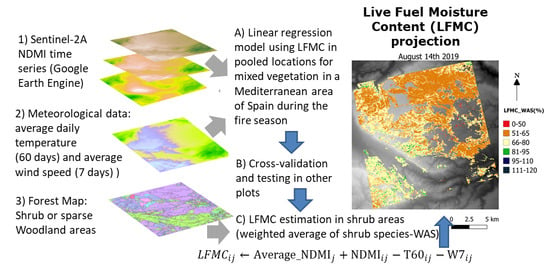
2. Materials and Methods
2.1. Study Area
2.2. Field Data
2.3. Remote Sensing Data
2.4. Meteorological Data
2.5. Statistical Analysis
- Analyze the seasonal variation of LFMC across species to assess for different water strategies in the study area.
- Assess the performance of different spectral indices on predicting LMFC_WAS across single locations, accounting also for meteorological information.
- Assess the performance of spectral indices on predicting LMFC_WAS in pooled locations considering site spectral characteristics (e.g., the average of the time series of the selected SI). The inclusion of long-term (cumulative) meteorological data was also evaluated to improve pooled site model predictions.
- Forward stepwise linear regression models were also applied considering all calibration plots from Table 1 distributed in the study area.
- The evaluation of the models was done using 10-fold cross-validation with 3 repetitions and leave-one-site-out cross validation.
- The precision of the best pooled site regression model was tested in the 5 additional plots of Table 2.
- Final regression model was applied to generate maps of LFMC_WAS estimations using Sentinel-2 images at 10 m/pixel spatial resolution.
3. Results
3.1. Variation of LFMC across Species and Individual Site Regressions
3.2. Pooled Site Regressions
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Plot Number | Model with Constant + NDMI + T30 | Model with Constant + Average_NDMI + NDMI + T60 + W7 | Model with Constant + Average_NDMI + NDMI + T60 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Plot | R-Squared | RMSE | MAE | R-Squared | RMSE | MAE | R-Squared | RMSE | MAE |
| 1 | 0.56 | 7.48 | 5.62 | 0.52 | 7.67 | 5.55 | 0.44 | 9.08 | 6.37 |
| 2 | 0.94 | 3.85 | 3.23 | 0.92 | 4.87 | 3.84 | 0.98 | 3.45 | 3.07 |
| 3 | 0.85 | 10.25 | 8.19 | 0.81 | 11 | 8.86 | 0.79 | 11.36 | 9.36 |
| 4 | 0.76 | 11.64 | 9.73 | 0.66 | 11.9 | 10.2 | 0.70 | 12.44 | 10.08 |
| 5 | 0.61 | 12.72 | 10.39 | 0.67 | 7.35 | 5.43 | 0.69 | 9.87 | 7.8 |
| 6 | 0.81 | 6.38 | 5.33 | 0.83 | 6.33 | 4.86 | 0.74 | 8.09 | 5.85 |
| 7 | 0.94 | 5.84 | 5.03 | 0.90 | 6.95 | 6.07 | 0.90 | 7.04 | 5.9 |
| 8 | 0.56 | 8.35 | 6.63 | 0.45 | 9.31 | 7.89 | 0.50 | 8.59 | 7.13 |
| 9 | 0.90 | 6.72 | 5.5 | 0.88 | 5.46 | 4.43 | 0.94 | 5.89 | 5.37 |
| 10 | 0.92 | 6.59 | 5.92 | 0.86 | 9.13 | 7.49 | 0.86 | 7.7 | 6.68 |
| 11 | 0.85 | 12.45 | 11.21 | 0.77 | 12.4 | 11.6 | 0.85 | 12.82 | 11.59 |
| 12 | 0.64 | 12.16 | 8.37 | 0.90 | 8.57 | 6.58 | 0.88 | 10.59 | 6.52 |
| 13 | 0.81 | 7.75 | 5.21 | 0.92 | 5 | 4.37 | 0.86 | 6.87 | 5.57 |
| 14 | 0.69 | 8.48 | 7.48 | 0.58 | 9.44 | 7.87 | 0.58 | 9.88 | 8.19 |
| 15 | 0.71 | 5.38 | 4.69 | 0.67 | 6.46 | 5.07 | 0.81 | 4.68 | 4.07 |
| Aver. | 0.77 | 8.40 | 6.83 | 0.76 | 8.12 | 6.67 | 0.76 | 8.56 | 6.90 |
Appendix B
| Spatial Resolution of Predictors | Formulation | p-Values | R2adj | RMSE | MAE |
|---|---|---|---|---|---|
| 3 × 3 Sentinel-2 pixels | <0.0000, <0.0000, <0.0000, <0.0000 <0.0000 | 0.72 | 7.80% | 5.95% | |
| 9 × 9 Sentinel-2 pixels | <0.0000, <0.0000 <0.0000, <0.0000, <0.0000 | 0.68 | 8.33% | 6.55% |
References
- Dimitriou, A.; Mantakas, G.; Kouvelis, S. An Analysis of Key Issues that Underlie Forest Fires and Shape Subsequent Fire Management Strategies in 12 Countries in the Mediterranean Basin; Final report prepared by Alcyon for WWF Mediterranean Programme Office and IUCN. 2001. Available online: https://ec.europa.eu/environment/forests/pdf/meeting140504_wwfsecondocument.pdf (accessed on 31 August 2021).
- Pausas, J.G.; Llovet, J.; Rodrigo, A.; Vallejo, V.R. Are wildfires a disaster in the Mediterranean basin?—A review. Int. J. Wildland Fire 2008, 17, 713–723. [Google Scholar] [CrossRef]
- He, T.; Lamont, B.B.; Pausas, J.G. Fire as a key driver of Earth’s biodiversity. Biol. Rev. 2019, 94, 1983–2010. [Google Scholar] [CrossRef]
- Tedim, F.; Leone, V.; Amraoui, M.; Bouillon, C.; Coughlan, M.R.; Delogu, G.M.; Fernandes, P.M.; Ferreira, C.; McCaffrey, S.; McGee, T.K.; et al. Defining Extreme Wildfire Events: Difficulties, Challenges, and Impacts. Fire 2018, 1, 9. [Google Scholar] [CrossRef] [Green Version]
- San-Miguel-Ayanz, J.; Durrant, T.H.; Boca, R.; Liberta, G.; Branco, A.; de Rigo, G.; Ferrari, D.; Maianti, P.; Vivancos, T.; Oom, D.; et al. Forest Fires in Europe, Middle East and North Africa 2018; Technical Report EUR 29856 EN; Publications Office of the European Union: Luxembourg, 2019; ISBN 978-92-76-12591-4. [Google Scholar] [CrossRef]
- Ribeiro, L.; Viegas, D.; Almeida, M.; McGee, T.K.; Pereira, M.G.; Parente, J.; Xanthopoulos, G.; Leone, V.; Delogu, G.M.; Hardin, H. Extreme wildfires and disasters around the world. In Extreme Wildfire Events and Disasters, Root Causes and New Management Strategies; Elsevier: Amsterdam, The Netherlands, 2020; pp. 31–51. [Google Scholar] [CrossRef]
- Dupuy, J.-L.; Fargeon, H.; Martin-StPaul, N.; Pimont, F.; Ruffault, J.; Guijarro, M.; Hernando, C.; Madrigal, J.; Fernandes, P. Climate change impact on future wildfire danger and activity in southern Europe: A review. Ann. For. Sci. 2020, 77, 1–24. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E. The 10% wind speed rule of thumb for estimating a wildfire’s forward rate of spread in forests and shrublands. Ann. For. Sci. 2019, 76, 44. [Google Scholar] [CrossRef] [Green Version]
- Brown, A.A.; Davis, K.P. Fire Danger Rating. In Forest Fire: Control and Use, 2nd ed.; Mac Graw Hill: New York, NY, USA, 1973; pp. 217–259. [Google Scholar]
- Sharma, S.; Carlson, J.D.; Krueger, E.S.; Engle, D.M.; Twidwell, D.; Fuhlendorf, S.D.; Patrignani, A.; Feng, L.; Ochsner, T.E. Soil moisture as an indicator of growing-season herbaceous fuel moisture and curing rate in grasslands. Int. J. Wildland Fire 2021, 30, 57–69. [Google Scholar] [CrossRef]
- Chuvieco, E.; Aguado, I.; Yebra, M.; Nieto, H.; Salas, J.; Martin, M.P.; Vilar, L.; Martínez, J.; Martín, S.; Ibarra, P.; et al. Development of a framework for fire risk assessment using remote sensing and geographic information system technologies. Ecol. Model. 2010, 221, 46–58. [Google Scholar] [CrossRef]
- Fares, S.; Bajocco, S.; Salvati, L.; Camarretta, N.; Dupuy, J.-L.; Xanthopoulos, G.; Guijarro, M.; Madrigal, J.; Hernando, C.; Corona, P. Characterizing potential wildland fire fuel in live vegetation in the Mediterranean region. Ann. For. Sci. 2017, 74, 1. [Google Scholar] [CrossRef] [Green Version]
- Martin-StPaul, N.; Pimont, F.; Dupuy, J.L.; Rigolot, E.; Ruffault, J.; Fargeon, H.; Cabane, E.; Duché, Y.; Savazzi, R.; Toutchkov, M. Live fuel moisture content (LFMC) time series for multiple sites and species in the French Mediterranean area since 1996. Ann. For. Sci. 2018, 75, 57. [Google Scholar] [CrossRef] [Green Version]
- Yebra, M.; Scortechini, G.; Badi, A.; Beget, M.E.; Boer, M.M.; Bradstock, R.; Chuvieco, E.; Danson, F.M.; Dennison, P.; De Dios, V.R.; et al. Globe-LFMC, a global plant water status database for vegetation ecophysiology and wildfire applications. Sci. Data 2019, 6, 155. [Google Scholar] [CrossRef] [Green Version]
- Gabriel, E.; Delgado-Dávila, R.; De Cáceres, M.; Casals, P.; Tudela, A.; Castro, X. Live fuel moisture content time series in Catalonia since 1998. Ann. For. Sci. 2021, 78, 1–10. [Google Scholar] [CrossRef]
- Yebra, M.; Dennison, P.; Chuvieco, E.; Riano, D.; Zylstra, P.; Hunt, E.R.; Danson, F.; Qi, Y.; Jurdao, S. A global review of remote sensing of live fuel moisture content for fire danger assessment: Moving towards operational products. Remote Sens. Environ. 2013, 136, 455–468. [Google Scholar] [CrossRef]
- Luo, K.; Quan, X.; He, B.; Yebra, M. Effects of Live Fuel Moisture Content on Wildfire Occurrence in Fire-Prone Regions over Southwest China. Forests 2019, 10, 887. [Google Scholar] [CrossRef] [Green Version]
- Arganaraz, J.P.; Landi, M.A.; Bravo, S.J.; Gavier-Pizarro, G.I.; Scavuzzo, C.M.; Bellis, L.M. Estimation of Live Fuel Moisture Content From MODIS Images for Fire Danger Assessment in Southern Gran Chaco. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5339–5349. [Google Scholar] [CrossRef]
- Bowman, D.; Williamson, G.; Yebra, M.; Lizundia-Loiola, J.; Pettinari, M.L.; Shah, S.; Bradstock, R.; Chuvieco, E. Wildfires: Australia needs national monitoring agency. Nature 2020, 584, 188–191. [Google Scholar] [CrossRef]
- Jolly, W.M.; Hadlow, A.M.; Huguet, K. De-coupling seasonal changes in water content and dry matter to predict live conifer foliar moisture content. Int. J. Wildland Fire 2014, 23, 480–489. [Google Scholar] [CrossRef] [Green Version]
- Viegas, D.; Pinol, J.; Viegas, M.T.; OgayaD, R. Estimating live fine fuels moisture content using meteorologically-based indices. Int. J. Wildland Fire 2001, 10, 223. [Google Scholar] [CrossRef]
- Helman, D.; Lensky, I.M.; Tessler, N.; Osem, Y. A Phenology-Based Method for Monitoring Woody and Herbaceous Vegetation in Mediterranean Forests from NDVI Time Series. Remote Sens. 2015, 7, 12314–12335. [Google Scholar] [CrossRef] [Green Version]
- Ruffault, J.; Martin-StPaul, N.; Pimont, F.; Dupuy, J.-L. How well do meteorological drought indices predict live fuel moisture content (LFMC)? An assessment for wildfire research and operations in Mediterranean ecosystems. Agric. For. Meteorol. 2018, 262, 391–401. [Google Scholar] [CrossRef]
- Castro, F.; Tudela, A.; Sebastià, M.T. Modeling moisture content in shrubs to predict fire risk in Catalonia (Spain). Agric. For. Meteorol. 2003, 116, 49–59. [Google Scholar] [CrossRef]
- Pellizzaro, G.; Cesaraccio, C.; Duce, P.; Ventura, A.; Zara, P. Relationships between seasonal patterns of live fuel moisture and meteorological drought indices for Mediterranean shrubland species. Int. J. Wildland Fire 2007, 16, 232–241. [Google Scholar] [CrossRef]
- Gao, B.-C.; Goetzt, A.F. Retrieval of equivalent water thickness and information related to biochemical components of vegetation canopies from AVIRIS data. Remote Sens. Environ. 1995, 52, 155–162. [Google Scholar] [CrossRef]
- Lasaponara, R. Inter-comparison of AVHRR-based fire susceptibility indicators for the Mediterranean ecosystems of southern Italy. Int. J. Remote Sens. 2005, 26, 853–870. [Google Scholar] [CrossRef]
- García, M.; Chuvieco, E.; Nieto, H.; Aguado, I. Combining AVHRR and meteorological data for estimating live fuel moisture content. Remote Sens. Environ. 2008, 112, 3618–3627. [Google Scholar] [CrossRef]
- Yebra, M.; Chuvieco, E.; Riaño, D. Estimation of live fuel moisture content from MODIS images for fire risk assessment. Agric. For. Meteorol. 2008, 148, 523–536. [Google Scholar] [CrossRef]
- Chuvieco, E.; Cocero, D.; Riaño, D.; Martin, P.; Martínez-Vega, J.; de la Riva, J.; Pérez, F. Combining NDVI and surface temperature for the estimation of live fuel moisture content in forest fire danger rating. Remote Sens. Environ. 2004, 92, 322–331. [Google Scholar] [CrossRef]
- Dennison, P.E.; Roberts, D.A.; Peterson, S.H.; Rechel, J. Use of Normalized Difference Water Index for monitoring live fuel moisture. Int. J. Remote Sens. 2005, 26, 1035–1042. [Google Scholar] [CrossRef]
- Quan, X.; He, B.; Yebra, M.; Yin, C.; Liao, Z.; Li, X. Retrieval of forest fuel moisture content using a coupled radiative transfer model. Environ. Model. Softw. 2017, 95, 290–302. [Google Scholar] [CrossRef]
- Marino, E.; Yebra, M.; Guillén-Climent, M.; Algeet, N.; Tomé, J.L.; Madrigal, J.; Guijarro, M.; Hernando, C. Investigating Live Fuel Moisture Content Estimation in Fire-Prone Shrubland from Remote Sensing Using Empirical Modelling and RTM Simulations. Remote Sens. 2020, 12, 2251. [Google Scholar] [CrossRef]
- Myoung, B.; Kim, S.H.; Nghiem, S.V.; Jia, S.; Whitney, K.; Kafatos, M.C. Estimating Live Fuel Moisture from MODIS Satellite Data for Wildfire Danger Assessment in Southern California USA. Remote Sens. 2018, 10, 87. [Google Scholar] [CrossRef] [Green Version]
- Peterson, S.H.; Roberts, D.A.; Dennison, P. Mapping live fuel moisture with MODIS data: A multiple regression approach. Remote Sens. Environ. 2008, 112, 4272–4284. [Google Scholar] [CrossRef]
- Caccamo, G.; Chisholm, L.A.; Bradstock, R.A.; Puotinen, M.; Pippen, B.G. Monitoring live fuel moisture content of heathland, shrubland and sclerophyll forest in south-eastern Australia using MODIS data. Int. J. Wildland Fire 2012, 21, 257–269. [Google Scholar] [CrossRef]
- Qi, Y.; Dennison, P.; Spencer, J.; Riano, D. Monitoring Live Fuel Moisture Using Soil Moisture and Remote Sensing Proxies. Fire Ecol. 2012, 8, 71–87. [Google Scholar] [CrossRef]
- Jia, S.; Kim, S.H.; Nghiem, S.V.; Cho, W.; Kafatos, M.C. Estimating Live Fuel Moisture in Southern California Using Remote Sensing Vegetation Water Content Proxies. In Proceedings of the IGARSS 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 5887–5890. [Google Scholar] [CrossRef]
- Chuvieco, E.; Aguado, I.; Salas, J.; García, M.; Yebra, M.; Oliva, P. Satellite Remote Sensing Contributions to Wildland Fire Science and Management. Curr. For. Rep. 2020, 6, 81–96. [Google Scholar] [CrossRef]
- Shu, Q.; Quan, X.; Yebra, M.; Liu, X.; Wang, L.; Zhang, Y. Evaluating the Sentinel-2a Satellite Data for Fuel Moisture Content Retrieval. In Proceedings of the IGARSS 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 9416–9419. [Google Scholar] [CrossRef]
- Lunetta, R.S.; Knight, J.F.; Ediriwickrema, J.; Lyon, J.G.; Worthy, L.D. Land-cover change detection using multi-temporal MODIS NDVI data. Remote Sens. Environ. 2006, 105, 142–154. [Google Scholar] [CrossRef]
- Stow, D.; Niphadkar, M. Stability, normalization and accuracy of MODIS-derived estimates of live fuel moisture for southern California chaparral. Int. J. Remote Sens. 2007, 28, 5175–5182. [Google Scholar] [CrossRef]
- García, M.; Riaño, D.; Yebra, M.; Salas, J.; Cardil, A.; Monedero, S.; Ramirez, J.; Martín, M.P.; Vilar, L.; Gajardo, J.; et al. A Live Fuel Moisture Content Product from Landsat TM Satellite Time Series for Implementation in Fire Behavior Models. Remote Sens. 2020, 12, 1714. [Google Scholar] [CrossRef]
- Costa, M. La Vegetació al País Valencià; Universitat de València: València, Spain, 1986; ISBN 84-370-0277-X. [Google Scholar]
- Gao, B.-C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.; Gao, X.; Ferreira, L. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.W.; Schell, J.A.; Deering, D.H.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Greenwave Effect) of Natural Vegetation; Type III Final Report; NASA/GSFC: Greenbelt, MD, USA, 1974. [Google Scholar]
- Pearson, R.L.; Miller, L.D. Remote mapping of standing crop biomass for estimation of the productivity of the shortgrass prairie, Pawnee National Grasslands, Colorado. In Proceedings of the 8th International Symposium on Remote Sensing of the Environment II, Ann Arbor, MI, USA, 2–6 October 1972; pp. 1355–1379. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef] [Green Version]
- Huntjr, E.; Rock, B. Detection of changes in leaf water content using Near- and Middle-Infrared reflectances. Remote Sens. Environ. 1989, 30, 43–54. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J. NMDI: A normalized multi-band drought index for monitoring soil and vegetation moisture with satellite remote sensing. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Piragnolo, M.; Lusiani, G.; Pirotti, F. Comparison of vegetation indices from rpas and sentinel-2 imagery for detecting permanent pastures. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-3, 1381–1387. [Google Scholar] [CrossRef] [Green Version]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Garnier, E.; Shipley, B.; Roumet, C.; Laurent, G. A standardized protocol for the determination of specific leaf area and leaf dry matter content. Funct. Ecol. 2001, 15, 688–695. [Google Scholar] [CrossRef]
- Yang, Y.; Luo, J.; Huang, Q.; Wu, W.; Sun, Y. Weighted Double-Logistic Function Fitting Method for Reconstructing the High-Quality Sentinel-2 NDVI Time Series Data Set. Remote Sens. 2019, 11, 2342. [Google Scholar] [CrossRef] [Green Version]
- De Cáceres, M.; Martin-StPaul, N.; Turco, M.; Cabon, A.; Granda, V. Estimating daily meteorological data and downscaling climate models over landscapes. Environ. Model. Softw. 2018, 108, 186–196. [Google Scholar] [CrossRef]
- Milliken, G.A.; Johnson, D.E. Analysis of Messy Data; Chapman & Hall/CRC: Boca Raton, FL, USA, 1992; Volume 1. [Google Scholar]
- Vrieze, S.I. Model selection and psychological theory: A discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). Psychol. Methods 2012, 17, 228–243. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Imdadullah, M.; Aslam, M.; Altaf, S. mctest: An R Package for Detection of Collinearity among Regressors. R J. 2016, 8, 495–505. [Google Scholar] [CrossRef]
- Marino, E.; Al., E. Estimation of live fuel moisture content of shrubland using MODIS and Sentinel-2 images. In Advances in Forest Fire Research 2018; Chapter 2—Fuel Management; Proceedings of the VIII Inter-National Conference on Forest Fire Research, Coimbra, Portugal, 10–16 November 2018; Viegas, D.X., Ed.; Imprensa da Universidade de Coimbra: Coimbra, Portugal, 2018; pp. 218–226. [Google Scholar] [CrossRef] [Green Version]
- Jolly, W.M.; Hintz, J.; Linn, R.L.; Kropp, R.C.; Conrad, E.T.; Parsons, R.A.; Winterkamp, J. Seasonal variations in red pine (Pinus resinosa) and jack pine (Pinus banksiana) foliar physio-chemistry and their potential influence on stand-scale wildland fire behavior. For. Ecol. Manag. 2016, 373, 167–178. [Google Scholar] [CrossRef] [Green Version]









| Plot Number | Zone Code | Altitude (m) | Slope (%) | Aspect (Degrees) | Species (% FCC) |
|---|---|---|---|---|---|
| 1 | A | 270 | 15.4 | 179 | Pinus halepensis (35), Rosmarinus Officinalis (25), Quercus coccifera (20), Erica multiflora (20), Pistacia lentiscus (20), Chamaerops humilis (15) |
| 2 | A | 302 | 12.5 | 157 | Pinus halepensis (20), Rosmarinus officinalis (30), Quercus coccifera (10), Phillyrea angustifolia (12), Pistacia lentiscus (17), Chamaerops humilis (15) |
| 3 | B | 217 | 5.7 | 127 | Pinus halepensis (20), Rosmarinus officinalis (30), Rhamnus lycioides (12), Juniperus oxycedrus (10), Pistacia lentiscus (7) |
| 4 | B | 203 | 3.4 | 90 | Pinus halepensis (40), Rosmarinus officinalis (35), Quercus coccifera (5), Juniperus oxycedrus (20), Rhamnus lycioides (10), Erica multiflora (1), Pistacia lentiscus (3), Stipa tenacissima (30) |
| 5 | C | 957 | 11.1 | 353 | Pinus halepensis (10), Rosmarinus officinalis (15), Quercus coccifera (40), Juniperus oxycedrus (15), Quercus ilex (35), Juniperus phoenicea (10) |
| 6 | D | 234 | 9.8 | 244 | Pinus halepensis (7), Rosmarinus officinalis (30), Quercus coccifera (45), Juniperus oxycedrus (5), Erica multiflora (15) |
| 7 | D | 267 | 16.9 | 76 | Pinus halepensis (15), Rosmarinus officinalis (25), Quercus coccifera (35), Cistus albidus (3), Erica multiflora (20) |
| 8 | E | 548 | 22.5 | 112 | Pinus halepensis (20), Rosmarinus officinalis (30), Ulex parviflorus (10), Juniperus oxycedrus (15), Quercus coccifera (5), Erica multiflora (30) |
| 9 | E | 665 | 15.8 | 212 | Rosmarinus officinalis (50), Quercus coccifera (50), Ulex parviflorus (5), Juniperus oxycedrus (20), Erica multiflora (7) |
| 10 | E | 672 | 16.4 | 345 | Pinus halepensis (10), Rosmarinus officinalis (30), Quercus coccifera (50), Juniperus oxycedrus (30), Erica multiflora (7) |
| 11 | F | 883 | 3.2 | 355 | Pinus halepensis (5), Rosmarinus officinalis (20), Quercus coccifera (20), Quercus ilex (10), Juniperus oxycedrus (10), Cistus albidus (3) |
| 12 | F | 873 | 6.0 | 73 | Quercus ilex (15), Rosmarinus officinalis (10), Quercus coccifera (30), Juniperus oxycedrus (10), Cistus albidus (3) |
| 13 | F | 882 | 2.0 | 45 | Rosmarinus officinalis (7), Quercus coccifera (10), Ulex parviflorus (3), Juniperus oxycedrus (20), Quercus ilex (15) |
| 14 | G | 577 | 18.8 | 92 | Erica multiflora (10), Quercus coccifera (60), Rosmarinus officinalis (30), Quercus ilex (20), Cistus ladanifer (5) |
| 15 | G | 390 | 16.7 | 0 | Erica multiflora (20), Quercus ilex (20), Quercus coccifera (40), Pistacia lentiscus (5), Ulex parviflorus (10) |
| Plot Number | Zone Code | Altitude (m) | Slope (%) | Aspect (Degrees) | %FCC Species |
|---|---|---|---|---|---|
| 16 | A | 323 | 12.4 | 231 | Pinus halepensis (70), Rosmarinus Officinalis (40), Erica multiflora (3), Pistacia lentiscus (30), Phillyrea angustifolia (20) |
| 17 | A | 299 | 9.2 | 150 | Pinus halepensis (15), Ulex parviflorus (10), Quercus coccifera (12), Pistacea lentiscus (20), Stipa tenacissima (40), Chamaerops humilis (15) |
| 18 | C | 740 | 12.9 | 36 | Pinus halepensis (20), Rosmarinus officinalis (10), Arbutus unedo (20), Juniperus oxycedrus (30), Erica multiflora (15), Ulex parviflorus (10) |
| 19 | D | 321 | 29.8 | 224 | Pinus halepensis (70), Rosmarinus officinalis (20), Quercus coccifera (35), Rhamnus lycioides(10), Erica multiflora (20) |
| 20 | D | 301 | 5.6 | 15 | Pinus halepensis (80), Rhamnus lycioides (15), Quercus coccifera (40), Pistacia lentiscus (20), Erica multiflora (15) |
| Spectral Index | Formulation for Sentinel-2 |
|---|---|
| Enhanced Vegetation Index [46] | EVI = 2.5 × (B8 − B4)/(B8 + 6 × B4 − 7.5 × B2 + 1) |
| Soil Adjusted Vegetation Index [47] | SAVI = ((B8 − B4)/(B8 + B4 + 0.5)) × 1.5 |
| Optimized Soil Adjusted Vegetation Index [48] | OSAVI = (1 + 0.16) × (B8 − B4)/(B8 + B4 + 0.16) |
| Normalized Difference Vegetation Index [49] | NDVI = (B8 − B4)/(B8 + B4) |
| Ratio Vegetation Index [50] | RVI = B8/B4 |
| Visible Atmospherically Resistant Index [51] | VARI = (B3 − B4)/(B3 + B4 − B2) |
| Normalized Difference Moisture Index [52] | NDMI = (B8 − B11)/(B8 + B11) |
| Normalized Multi-band Drought Index [53] | - |
| Normalized Difference Water Index [54] | NDWI = (B8 − B12)/(B8 + B12) |
| Vegetation Index-Green [55] | VIgreen = (B3 − B5)/(B3 + B5) |
| Transformed Chlorophyll Absorption Index [56] | TCARI = 3 × ((B5 - B4) − 0.2 × (B5 − B3) * (B5/B4)) |
| Ratio TCARI-OSAVI [56] | TCARI_OSAVI = TCARI/OSAVI |
| Specific leaf area [57] | SLA = (B9)/(B5 + B12) |
| Plot Number | R2 of LFMC_WAS Model Using the Best Spectral Index | R2 of LFMC_WAS Model Using Forward Stepwise Linear Regression with the Following Predic-Tors: NDMI and T60 | R2 of LFMC_WAS Model Using Forward Stepwise Linear Regression with the Following Predictors: NDMI, NMDI, T60, T30, and W7 | |||
|---|---|---|---|---|---|---|
| 1 | 0.56 | NDMI | 0.56 | NDMI | 0.56 | NDMI |
| 2 | 0.95 | SAVI | 0.97 | NDMI+T60 | 0.97 | NDMI + T30 |
| 3 | 0.59 | EVI | 0.46 | T60 | 0.75 | T30 |
| 4 | 0.57 | NDMI | 0.57 | NDMI | 0.83 | T30 + T60 |
| 5 | 0.86 | TCARI_OSAVI | 0.67 | T60 | 0.67 | T60 |
| 6 | 0.77 | NMDI | 0.64 | NDMI | 0.92 | T30 + W7 |
| 7 | 0.85 | NDMI | 0.85 | NDMI | 0.95 | T30 + T60 |
| 8 | 0.79 | SLA | 0.52 | NDMI | 0.52 | NDMI |
| 9 | 0.77 | NMDI | 0.94 | NDMI + T60 | 0.96 | NMDI + T30 |
| 10 | 0.71 | NDMI | 0.87 | NDMI + T60 | 0.87 | T30 |
| 11 | 0.86 | OSAVI | 0.78 | T60 | 0.83 | T30 |
| 12 | 0.71 | NDMI | 0.88 | T60 | 0.88 | T60 |
| 13 | 0.65 | NMDI | 0.86 | T60 | 0.95 | T60 + W7 |
| 14 | 0.66 | NMDI | 0.51 | NDMI | 0.84 | NMDI + T30 |
| 15 | 0.66 | NMDI | 0.77 | T60 | 0.77 | T60 |
| Model | Formulation | p-Values | VIF | R2adj | RMSE | MAE |
|---|---|---|---|---|---|---|
| SLR1 | <0.0000 | 0.29 | 12.46% | 9.93% | ||
| <0.0000 | 1.0 | |||||
| SLR2 | 0.6428 | 0.19 | 13.26% | 10.72% | ||
| <0.0000 | 1.0 | |||||
| AdLR | <0.0000 | 0.48 | 10.67%; | 8.42% | ||
| <0.0000 | 3.2329 | |||||
| <0.0000 | 3.2329 | |||||
| AdMLR | <0.0000 | 0.70 | 8.13% | 6.33% | ||
| 0.0008 | 4.1737 | |||||
| <0.0000 | 4.27214 | |||||
| <0.0000 | 1.54064 | |||||
| <0.0000 | 1.22462 | |||||
| MLR | <0.0000 | 0.66 | 8.54%; | 6.56% | ||
| <0.0000 | 1.07416 | |||||
| <0.0000 | 1.07416 |
| Plot | R-Squared | RMSE | MAE |
|---|---|---|---|
| 16 | 0.68 | 9.58% | 7.21% |
| 17 | 0.80 | 6.07% | 4.71% |
| 18 | 0.46 | 8.15% | 6.85% |
| 19 | 0.57 | 8.21% | 6.33% |
| 20 | 0.80 | 6.42% | 4.89% |
| All | 0.65 | 7.79% | 6.00% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa-Saura, J.M.; Balaguer-Beser, Á.; Ruiz, L.A.; Pardo-Pascual, J.E.; Soriano-Sancho, J.L. Empirical Models for Spatio-Temporal Live Fuel Moisture Content Estimation in Mixed Mediterranean Vegetation Areas Using Sentinel-2 Indices and Meteorological Data. Remote Sens. 2021, 13, 3726. https://doi.org/10.3390/rs13183726
Costa-Saura JM, Balaguer-Beser Á, Ruiz LA, Pardo-Pascual JE, Soriano-Sancho JL. Empirical Models for Spatio-Temporal Live Fuel Moisture Content Estimation in Mixed Mediterranean Vegetation Areas Using Sentinel-2 Indices and Meteorological Data. Remote Sensing. 2021; 13(18):3726. https://doi.org/10.3390/rs13183726
Chicago/Turabian StyleCosta-Saura, José M., Ángel Balaguer-Beser, Luis A. Ruiz, Josep E. Pardo-Pascual, and José L. Soriano-Sancho. 2021. "Empirical Models for Spatio-Temporal Live Fuel Moisture Content Estimation in Mixed Mediterranean Vegetation Areas Using Sentinel-2 Indices and Meteorological Data" Remote Sensing 13, no. 18: 3726. https://doi.org/10.3390/rs13183726
APA StyleCosta-Saura, J. M., Balaguer-Beser, Á., Ruiz, L. A., Pardo-Pascual, J. E., & Soriano-Sancho, J. L. (2021). Empirical Models for Spatio-Temporal Live Fuel Moisture Content Estimation in Mixed Mediterranean Vegetation Areas Using Sentinel-2 Indices and Meteorological Data. Remote Sensing, 13(18), 3726. https://doi.org/10.3390/rs13183726