1. Introduction
Compared with traditional panchromatic and multispectral remote sensing images, hyperspectral images (HSIs) contain rich spectral information owing to the hundreds of narrow contiguous wavelength bands. In addition, some spatial information from homogeneous areas is also incorporated into HSIs. Recently, HSIs have been widely used in various kinds of fields, such as land cover mapping [
1], change detection [
2], object detection [
3], vegetation analysis [
4], etc. With the rapid development of HSI technology, HSI classification has become a hot and valuable topic, which aims at assigning each pixel vector to a specific land cover class [
5,
6]. Due to the curse of dimensionality and the Hughes phenomenon [
7,
8], how to explore the plentiful spectral and spatial information of HSIs remains extremely challenging.
To take advantage of abundant spectral information, traditional HSI classification methods tend to take an original pixel vector as the input, such as
-nearest neighbors (KNNs) [
9], multinomial logistic regression (MLR) [
10], and linear discriminant analysis (LDA) [
11]. These methods mainly focus on two steps: feature engineering and classifier training. Feature engineering reduces the high dimensionality of the spectral pixel vector to capture effective features. Then, the extracted features are fed into a general-purpose classifier to yield the classification results. However, these spectral-based classifiers only concern spectral information while ignoring the spatial correlation and local consistency of HSI. Later, some spectral-spatial classifiers appeared for HSI classification, such as DMP-SVM [
12], Gabor-SVM [
13], and SVM-MRF [
14]. These methods improve the classification performance to a certain extent, such as approximately 10% overall accuracy on the popular Pavia University dataset. However, the aforementioned methods belong to shallow layer models, which have limited representation capacity to fully utilize the abundant spectral and spatial information of HSIs. Specifically, these models usually utilize handcrafted features, which cannot effectively reflect the characteristics of different objects. Consequently, they have poor adaptability to the spatial environment.
Recently, deep learning (DL) methods have achieved considerable breakthroughs in the field of computer vision [
15,
16,
17]. Along with the improvement of DL, many DL-based methods have been proposed for HSI classification. DL-based models usually have multiple hidden layers, which can combine low-level features to form abstract high-level feature representations. These features are closer to the intrinsic properties of the identified object compared to shallow features, which are more conducive for classification. Similar to the traditional methods exemplified above, DL-based methods can also be divided into two categories: spectral-based methods and spectral-spatial-based methods. The spectral-based methods primarily concern the rich spectral information from HSIs. For example, Hu et al. [
18] proposed a 1D CNN to classify HSIs directly in the spectral domain. Mou et al. [
19] exploited a novel RNN model for HSI classification for the first time to deal with hyperspectral pixels as sequential data and determined categories by network reasoning. Li et al. [
20] designed a novel pixel-pair method to reorganize training samples and used deep pixel-pair features for HSI classification. Zhan et al. [
21] proposed a novel generative adversarial network (GAN) to handle the problem of insufficient labeled HSI pixels. However, the spectral-based methods infer pixel labels by only using spectral signatures, which in the actual imaging process are easily disturbed by the atmospheric effects, instrument noises, and incident illumination [
22,
23]. Consequently, the results generated by these models are also unsatisfactory.
Different from spectral-based methods, spectral-spatial-based methods extract both spectral and spatial information for classification. For example, Chen et al. [
24] used the stacked autoencoder (SAE) to extract spectral and spatial features and then used logistic regression as the classifier. Chen et al. [
25] adopted a novel 3D-CNN model combined with regularization to extract spectral-spatial features for classification. Roy et al. [
26] proposed a model named HybridSN, which includes a spectral-spatial 3D-CNN followed by spatial 2D-CNN to facilitate the joint spectral-spatial feature representations and spatial feature representations. Inspired by the residual network [
27], Zhong et al. [
28] proposed a spectral–spatial residual network (SSRN), which extracts spectral features and spatial features sequentially. Based on SSRN and DenseNet [
29], Wang et al. [
30] proposed a fast densely-connected spectral–spatial convolution network (FDSSC) for HSI classification. Although the CNN-based methods mentioned above can extract abundant spectral and spatial signals from HSI cubes, the spectral responses of these signals may vary from band to band; likewise, the importance of spatial information may also vary from location to location. In other words, different spectral channels or spatial positions of feature maps may have different contributions to the classification. It is desired to recalibrate the feature responses of spectral channels or spatial positions adaptively, emphasizing informative features and suppressing less useful ones.
The attention mechanism (AM) is proposed as an analogy to the processing mechanism of human vision, which enables models to focus on key pieces of the feature space and differentiate irrelevant information. With the rapid progress of AMs, more and more HSI classification models combined with AMs appeared. For example, Ma et al. [
31] proposed a double-branch multi-attention mechanism network (DBMA) for HSI classification. The DBMA applies both the channel-wise attention and spatial-wise attention in the HSI classification task to emphasize informative features. However, the AMs in the DBMA have two drawbacks. On the one hand, they aggregate features by directly squeezing global spectral or spatial information, which inadequately utilizes global contextual information. On the other hand, they recalibrate the importance of channels and positions by the rescaling operation, which cannot effectively capture long-range feature dependencies. Then, Li et al. [
32] proposed a double-branch dual-attention mechanism network (DBDA) for HSI classification based on the DBMA and the DANet [
33]. The AMs in the DBDA consume considerable computing resources because of matrix multiplication operations when obtaining attention maps. The interactions among enhanced channels or positions are not well exploited.
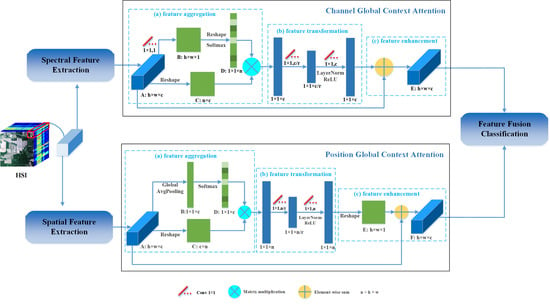
In order to alleviate the problems of AMs in the DBMA and the DBDA, we developed two novel AMs known as channel global context (GC) attention and position GC attention inspired by the GC block [
34]. The proposed channel GC attention and position GC attention can make full use of global contextual information with less time consumption. In addition, the interactions among enhanced channels or positions are modeled to learn high-level semantic feature representations. Concretely, our channel and position GC attentions can be abstracted into three procedures: (a) feature aggregation, which aggregates the features of all positions or channels via weighted summation under the aid of the channel or position attention map to yield global contextual features; (b) feature transformation, which learns the adaptive channel-wise or position-wise non-linear relationships by a bottleneck transform module consisting of two 1 × 1 convolutions, the ReLU activation function, and layer normalization; (c) feature enhancement, which merges the transformed global contextual information into features of all positions or channels by element-wise summation to capture long-range dependencies and obtain more powerful feature representations. To sum up, the main contributions of this paper are the following:
An end-to-end spectral-spatial framework with channel and position global context (GC) attention (SSGCA) is proposed for HSI classification. The SSGCA has two branches: the spectral branch with channel GC attention is used to capture spectral features, while the spatial branch with position GC attention is used to obtain spatial features. At the end of the network, spectral and spatial features are combined for HSI classification.
A channel GC attention and a position GC attention are proposed for feature enhancement in the spectral branch and the spatial branch, respectively. The channel GC attention is designed to capture interactions among channels, while the position GC attention is invented to explore interactions among positions. Both GC attentions can make full use of global contextual information with less time consumption and model long-range dependencies to obtain more powerful feature representations.
The SSGCA network is applied to three well-known public HSI datasets. Experimental results demonstrate that our network achieves the best performance compared with other well-known networks.
The remainder of this article is organized as follows.
Section 2 introduces the related work, and
Section 3 describes the proposed methodology in detail. Next, the experimental results and comprehensive analysis are reported in
Section 4 and
Section 5. Finally, some conclusions of this article are drawn in
Section 6.
2. Related Work
In this section, we introduce the related work that plays a significant role in our work, including 3D convolution operation, CNN-based methods for HSI classification, the dense connection block, and the attention mechanism (AM).
2.1. 3D Convolution Operation
The 3D convolution operation was first proposed in [
35] to compute features from both spatial and temporal dimensions for human action recognition. Later, various 3D CNN networks based on the 3D convolution operation were designed for HSI classification. For example, Chen et al. [
25] proposed a deep 3D CNN model, which employed several 3D convolutional and pooling layers to extract deep spectral-spatial feature maps for classification. Different from [
25], Li et al. [
36] designed a 3D CNN network, which stacks 3D convolutional layers without the pooling layer to extract deep spectral-spatial-combined features effectively. Furthermore, Roy et al. [
26] proposed a hybrid model named HybridSN which consists of 3D CNN based on 3D convolution and 2D CNN based on 2D convolution to facilitate the joint spectral-spatial feature representations and spatial feature representations. To sum up, 1D convolution extracts spectral features, whereas 2D convolution extracts local spatial features; unlike 1D and 2D convolution, 3D convolution allows extracting spatial and spectral information simultaneously.
In this paper, 3D convolution is employed as a fundamental element playing a crucial role in the feature extraction stage. At the same time, BN [
37] and the ReLU activation function are attached to each 3D convolution operation in our network, which can accelerate the learning rate of DL models and assist the network to learn non-linear feature relationships, respectively. The 3D convolution operation can be formulated as [
35]:
where
l indicates the layer that is discussed,
i is the number of feature maps in this layer,
represents the output at position
on the
ith feature maps of the
lth layer,
,
, and
stand for the height, width, and channel number of the 3D convolution kernel, respectively,
j indexes the feature maps in the
th layer connected to the current feature maps,
is the value at position
of the kernel corresponding to the
jth feature maps,
g is the activation function, and
b is the bias.
2.2. Cube-Based Methods for HSI Classification
Different from traditional pixel-based classification methods [
18,
19,
20] that only utilize spectral information, cube-based methods explore both spectral and spatial information from HSIs. Recently, many cube-based methods were proposed for HSI classification, such as DRCNN [
38], CDCNN [
39], DCPN [
40], and SSAN [
41]; these methods have attracted increasing attention and made considerable achievements. In the remainder of this section, we will briefly introduce the process of HSI classification with the aid of cube-based methods.
For a specific pixel of an HSI, a square HSI data cube is cropped, centered on this pixel, which is taken as the input data of the cube-based network, and the land cover label of the HSI cube is determined by its central pixel. Let represent the ith HSI data cube and represent the corresponding land cover label, where is the spatial size, c is the number of channels, and m is the number of land cover categories. Consequently, the ith sample can be denoted as , and all samples will be divided into three sets. To be specific, a certain number of samples are randomly selected as the training set; another certain number of samples are randomly assigned as the validation set; and the remaining samples are used as the testing set. The training set is fed into the network in batches to adjust the trainable parameters; the validation set acts as the monitor to observe the optimization process of the network, while the testing set serves to evaluate the classification performance of the network. In this article, the designed network is also cube-based, but the difference is that we introduce AMs into our network to enhance the extracted features and thus obtain more powerful feature representations for HSI classification.
2.3. Dense Connection Block
In order to alleviate the vanishing gradient problem, strengthen feature propagation, and encourage feature reuse, Gao et al. [
29] designed DenseNet, which introduces direct connections from any layer to all subsequent layers. Inspired by SSRN [
28] and DenseNet, Wang et al. [
30] proposed the FDSSC network for HSI classification to learn discriminative spectral and spatial features separately. The FDSSC consists of a spectral dense block, a reducing dimension block, and a spatial dense block. In the DBMA [
31] and DBDA [
32], the capability to extract features of dense connection blocks from the FDSSC was demonstrated once again. For this article, we also use the spectral dense block and spatial dense block from the FDSSC as the baseline network for feature extraction, and the difference is that the spectral and spatial branches are connected in parallel, the same as the DBMA and DBDA, rather than in a cascaded manner. These two dense connection blocks can reduce the high dimensionality and automatically learn more effective spatial and spectral features separately with little depletion of the computing resources.
As shown in
Figure 1 and
Figure 2, the spectral and spatial dense blocks consist of several sets of feature maps, direct connections, and 3D convolution operations. The BN operation and the ReLU activation function are also included. In the spectral dense block, the size of the 3D convolution kernels is
, the stride is
, and the manner of padding is “same”, which can ensure the output shape is the same as the input shape. The feature maps of the
lth layer receive feature maps from all previous outputs and the initial input. Consequently, if we set
as the
lth feature maps, we can calculate it by the previous
feature maps, as shown in the following equation:
where
refers to the concatenation of the previous feature maps.
includes batch normalization (BN), the ReLU activation function, and 3D convolution operations. Furthermore, the number of
lth input feature maps
can be calculated as follows:
where
is the number of initial feature maps and
k is the kernel number of the 3D convolution operation. In this paper, the spectral dense block consists of four layers; if the input shape is
, after the above analysis, we can know that the shape of the output remains
, and the channel number will change to
.
In the spatial dense block, the kernel size of 3D convolution is
, the manner of padding is “same”, and the stride is
. Same as spectral dense block, the feature maps of current layer have been linked to previous feature maps and back feature maps, and the final output is merged by all previous outputs and the initial input. As shown in
Figure 2, if the input shape is
, the shape of output feature maps remain
and the channel number will change into
after spatial dense block.
2.4. Attention Mechanism
Different spectral channel and spatial position features acquired by the DL-based network may provide different contributions to classification. Therefore, how to make models focus on the most informative part and differentiate low-correlation information is essential for classification. The AM was firstly presented in language translation [
42]. Immediately afterwards, it developed rapidly and acquired incredible breakthroughs in the field of computer vision. For example, Hu et al. [
43] invented a squeeze-and-excitation network (SENet) to adaptively refine the channel-wise feature response by modeling interdependencies among channels, which brings significant improvements to the performance of CNNs. Different from SENet, Woo et al. [
44] proposed a convolutional block attention module (CBAM), which exploits attention in both the channel and position dimensions to learn what and where to emphasize or suppress, aiming at refining intermediate features effectively. With the purpose of capturing long-range dependencies, Wang et al. [
45] presented non-local operations as a generic family of building blocks for capturing long-range dependencies, which compute the response at a position as a weighted sum of the features at all positions. Inspired by the non-local block from [
45] and the SE block from [
43], Yue Cao et al. [
34] proposed a global context (GC) block, which is lightweight and can model the global context more effectively.
Recently, AMs have received increasing attention in the field of remote sensing. Since HSIs contain more abundant information, especially in the spectral dimension, it is critical to avoid the impact of redundant information while utilizing useful information efficiently. Therefore, plenty of DL-based methods combined with various kinds of AMs have been designed for HSI classification, such as SSAN [
41], the DBMA [
31], the DBDA [
32], and so on. These networks further improved the classification performance with the assistance of AMs; however, previous AMs attached to CNN-based networks for HSI classification have some insufficiencies. For example, they inadequately utilize global contextual information and cannot model long-range dependencies effectively; in addition, they are time-consuming and cannot learn non-linear feature relationships. To tackle these issues, the GC block [
34] employed in the field of general images seems to work. However, the GC block only focuses on the channel dimension, and in the HSI data cube, the position characteristics also play a crucial role in classification. Therefore, we invented a position-wise framework resembling the GC block, aiming at processing the position information of HSIs. These two frameworks called channel GC attention and position GC attention are attached to the spectral and spatial branch to optimize the features, avoiding the disadvantages of previous AMs. The implementation details of our channel GC attention and position GC attention are described in
Section 3.1 and
Section 3.2.
4. Experiments
4.1. Datasets
In this paper, we selected three well-known HSI datasets to evaluate the effectiveness of our network compared with other widely used methods proposed before. The selected datasets include Indian Pines (IN), University of Pavia (UP), and the Salinas Valley (SV) dataset.
The IN dataset was captured by the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) over the Indian Pines test site in northwestern Indiana in 1992, and the image contains 16 vegetation classes and has pixels with a spatial resolution of 20 m per pixel. After removing 20 water absorption bands, this dataset includes 200 spectral bands for analysis ranging from 400 to 2500 nm.
The UP dataset was acquired over the city of Pavia, Italy, in 2002 by an airborne instrument—the Reflective Optics Spectrographic Imaging System (ROSIS). This dataset consists of pixels with a 1.3 m per pixel spatial resolution and 103 spectral bands ranging from 430 to 860 nm after removing 12 noisy bands. The dataset contains a large number of background pixels, so the total number of pixels including the features is only 42,776. There are 9 types of features, including asphalt roads, bricks, pastures, trees, bare soil, etc.
The SV dataset was also gathered by the AVIRIS sensor over the region of Salinas Valley, CA, USA, with a 3.7 m per pixel spatial resolution. The same as the IN dataset, twenty water absorption bands of the SV dataset were discarded. After that, the SV dataset consisted of 204 spectral bands and pixels for analysis from 400 to 2500 nm. The dataset presents 16 classes related to vegetables, vineyard fields, and bare soil.
In this paper, we randomly selected a few samples of each dataset for training and validation. To be specific, from the IN dataset, we selected 5% of the samples for training and 5% for validation. For the UP dataset, we selected 1% of the samples for training and 1% for validation. In addition, we also selected 1% as training samples and 1% as validation samples from the SV dataset.
Table 6,
Table 7 and
Table 8 list the sample numbers for the training, validation, and testing for the three datasets.
4.2. Evaluation Measures
In order to quantify the performance of the proposed method, four evaluation metrics were selected: the accuracy of each class, the overall accuracy (OA), the average accuracy (AA), and the kappa coefficient. The OA is the ratio of the number of correctly classified HSI pixels to the total number of HSI pixels in the testing samples. The AA is the mean of the accuracies for different land cover categories. Kappa measures the consistency between the classification results and the ground truth. Let
represent the confusion matrix of the classification results, where m denotes the number of land cover categories. The values of the OA, AA, and kappa can be calculated as follows [
47]:
where
is a vector of the diagonal elements of
M,
represents the sum of all elements of the matrix,
represents the sum of the elements in each column,
represents the sum of the elements in each row,
represents the mean of all elements, and
represents the element-wise division.
4.3. Experimental Setting
In this paper, SVM with the RBF kernel [
48] and several well-known DL-based methods were selected for comparison, including SSRN [
28], the FDSSC [
30], the DBMA [
31], and the DBDA [
32]. To ensure the fairness of the comparative experiments, we adopted the same hyperparameter settings for these methods, and all experiments were executed on an NVIDIA GeForce GTX 2070 SUPER GPU with a memory of 32 GB. For the DL-based methods, the spatial size of the HSI cubes was set to
, the batch size was 64, and the number of training epochs was set to 200. Besides, a cross-entropy loss function was exploited to measure the difference between the predicted value and the real value to train the parameters of the networks, which can be formulated as follows:
where
m is the number of land cover categories,
denotes the land cover label (if the category is
j,
is 1; otherwise,
equals to 0), and
represents the probability that the category is
j, which is calculated by the softmax function. To prevent overfitting, the early stopping strategy was adopted. If the loss value of the validation dataset no longer decreases for 20 epochs, the training process will be stopped. Furthermore, the optimizer was set to Adam with a 0.001 learning rate, and we used the cosine annealing [
49] method to dynamically adjust the learning rate, which can prevent the model from falling into local minima. The learning rate was adjusted according to the following equation [
32,
49]:
where
is the learning rate within the
ith run and
is the range of the learning rate.
represents the count of epochs that were executed, and
controls the count of epochs that will be executed in a cycle of adjustment. Finally, a dropout layer was adopted in the bottleneck transform module of GC attentions to further avoid overfitting, and the dropout percentage
p was set to
.
4.4. Classification Results
Table 9,
Table 10 and
Table 11 show the OAs, AAs, kappa coefficients, and classification accuracies of each class for the three HSI datasets. Obviously, the proposed method SSGCA achieves the best OAs, AAs, and kappa coefficients compared with the other methods on the three HSI datasets, which can demonstrate the effectiveness and generalizability of our method. For example, when 5% of the samples are randomly selected for training on the IN dataset, our method achieves the best accuracy with 98.13% OA, improving 1.14% over the DBDA (96.99%), 1.35% over the DBMA (96.78%), 1.95% over the FDSSC (96.18%), and 2.68% over SSRN (95.45%). In contrast to SVM (74.74%), our method achieves a considerable improvement of more than 23% in terms of OA. Besides, from the results, we can learn that all the DL-based methods achieve higher performance than SVM on three HSI datasets. For example, the OAs of the DL-based methods obtain more than a 20% increase in contrast to SVM on the IN dataset and about a 10% increase on the UP and SV dataset. The reason is that DL-based methods can exploit high-level, abstract, and discriminative feature representations to improve the classification performance.
Furthermore, the classification results of the FDSSC, DBMA, and DBDA on the three datasets are higher than those of SSRN with approximately a 1–2% improvement in OA. These results demonstrate the effectiveness of a dense connection structure, which is adopted in the FDSSC, DBMA, and DBDA. Moreover, comparing the FDSSC to the three attention-based methods, we can find that the proposed SSGCA achieves a higher OA than the FDSSC for all three datasets; however, the results of the DBMA and DBDA are not always higher than those of the FDSSC. For instance, the OA of the DBDA is lower than the FDSSC on the UP and SV datasets, and the OA of the DBMA is below the FDSSC on the UP dataset. This means that our GC attentions can optimize the feature representations more effectively compared with the AMs in the DBMA and DBDA when these three methods employ the same feature extraction network. The reason is that our GC attentions can utilize global contextual information adequately, capture feature interactions well, and model long-range dependencies effectively. Finally, from the classification accuracies of each class for the three HSI datasets, we can find that our SSGCA achieves more stable results, benefiting from the invented GC attentions. Taking the SV dataset as an example, the best and worst single-category results of the SSGCA are 100% and 95.76%, respectively, with a difference of only 4.24%, while the difference is 8.82% for the DBDA (best: 100%; worst: 91.18%), 8.26% for the DBMA and FDSSC (best: 100%; worst: 91.74%), 12.16% for SSRN (best: 100%; worst: 87.84%), and 43.19% for SVM (best: 99.62%; worst: 56.43%).
Figure 6,
Figure 7 and
Figure 8 show the visualization maps of all methods along with the corresponding ground truth maps for the three HSI datasets. Firstly, from the visual classification results, we can intuitively conclude that the proposed SSGCA delivers the most accurate and smooth classification maps on all datasets, because the SSGCA can obtained more powerful feature representations with the aid of our GC attentions for classification. Secondly, compared to DL-based methods, the classification maps of SVM on the three datasets show plenty of mislabeled areas due to the lack of incorporation of spatial neighborhood information, and the extracted features are at a low-level. Thirdly, we can find that the visual classification maps of the attention-based methods are smoother than SSRN and the FDSSC, especially at the edges of land cover areas, and it can be observed that the SSGCA yields better classification maps in contrast to the DBDA and DBMA, because our GC attentions can adequately utilize global contextual information, learn nonlinear feature interactions, and model long range dependencies for feature enhancing compared with the attentions in the DBDA and DBMA.
5. Other Investigations
In this section, we conduct further investigations in the following three aspects. Firstly, different proportions of training samples from the three datasets are selected for all methods to investigate the performance of our method with different training sample numbers. Secondly, several ablation experiments are designed to investigate the effectiveness of our channel GC attention and position GC attention; meanwhile, we explore the effectiveness of different bottleneck ratio values in GC attentions. Thirdly, we report the total trainable parameter number and running time of all methods to investigate the computational efficiency of different methods.
5.1. Investigation of the Proportion of Training Samples
In this part, several experiments are designed to explore the robustness and generalizability of the proposed method with different training proportions. On the one hand, two percent, 3%, 7%, and 9% training samples were randomly selected from the IN dataset; on the other hand, zero-point-three percent, 0.5%, 0.7%, and 1.3% training samples were randomly selected from the UP and SV datasets.
Figure 9,
Figure 10 and
Figure 11 display the results for the different training ratios of the six methods on the three datasets.
Firstly, it is evident that different numbers of training samples bring about different classification performances for all methods: as the number of training samples increases, the classification accuracy increases, and the proposed method SSGCA achieves the best performance compared with other methods with different numbers of training samples on the three datasets. Secondly, the performance of the FDSSC is relatively poor when the training set is quite small compared to the DBMA, DBDA, and SSGCA, but as the training samples increase, the FDSSC outperforms the DBMA and DBDA, while the classification accuracy is closer to the best result, especially on the UP and SV datasets. From this comparison, we can learn that AMs have a more significant effect when lacking training samples. Thirdly, we can see that the accuracies of the DL-based methods get closer along with the increasing of the training samples, particularly on the IN and SV datasets.
5.2. Investigation of the Global Context Attentions
In this part, several ablation experiments are executed to demonstrate the effectiveness of the GC attentions in this article, including experiments only with the channel GC attention, experiments only with the position GC attention, and experiments without GC attentions. The training sample proportions of IN, UP, and SV in these experiments were 5%, 1%, and 1%, respectively, and the bottleneck ratio r was set to 16. It can be observed from
Figure 12 that both GC attentions can improve the classification performance on each dataset. For example, on the IN dataset, the channel GC attention brings an improvement of 0.37% OA, the position GC attention brings an improvement of 0.55% OA, and using both GC attentions can improve by 1% OA, which is a considerable advance in the case of limited training samples and high baseline accuracy. In addition, we can find that the channel GC attention plays a more significant role compared with the position GC attention on the IN and SV datasets, and the result is opposite on the UP dataset; however, the highest results can be achieved when both GC attentions are included in our network for all three datasets.
The bottleneck ratio r introduced in
Section 3.1 and
Section 3.2 is a hyperparameter, which aims to reduce the computational cost of our GC attentions. In this part, we also designed several experiments to explore the effectiveness of different values of the bottleneck ratio. The training sample proportions of IN, UP, and SV selected in these experiments were 5%, 1%, and 1%, respectively. The classification results reported in
Table 12 show that our SSGCA network acquires the highest performance when the bottleneck ratio r is set to 16 on the three datasets.
5.3. Investigation on Running Time
Table 13,
Table 14 and
Table 15 report the total number of trainable parameters of the DL-based methods. From the results, we can find that the SSGCA has fewer trainable parameters than the FDSSC, DBMA, and DBDA. Meanwhile,
Table 13,
Table 14 and
Table 15 show the training time and test time of all methods on the three datasets. Note that all experiments’ results were collected when the training sample proportions were 5%, 1%, and 1% on IN, UP, and SV, respectively, and the bottleneck ratio r of the SSGCA was set to 16. From these three tables, we can learn that SVM consumes less training and testing time than the DL-based methods. Furthermore, the proposed SSGCA spends the least training time and the second least testing time among all DL-based methods on the three datasets. Above all, we can conclude that the proposed SSGCA obtains the best classification performance with little time consumption, which can prove the high efficiency of our method.
6. Conclusions
In this article, an end-to-end spectral-spatial network with channel and position global context (GC) attention (SSGCA) is proposed for HSI classification. The proposed SSGCA is based on the work of many predecessors, including 3D convolution, DenseNet, the FDSSC, GCNet, the DBDA, and so on. The SSGCA mainly contains three stages: feature extraction, feature enhancement, and feature fusion classification. Feature extraction is based on dense connection blocks to acquire discriminative spectral and spatial features in two separate branches. Feature enhancement aims to optimize spectral and spatial feature representations to improve the classification performance by the channel GC attention and the position GC attention, respectively. Compared to the previous AMs used in HSI classification methods, our GC attentions can make full use of global contextual information and capture adaptive nonlinear feature relationships in the spectral and spatial dimensions with less computation consumption. Furthermore, our AMs can adequately model long-range dependencies. Feature fusion classification concatenates two types of features in the channel dimension, then the fusion features are fed into an FC layer with the softmax function to generate the final land cover category. Moreover, we designed a great quantity of experiments on three public HSI datasets to verify the effectiveness, generalizability, and robustness of our method. Later, analyses on the experimental results demonstrated that the proposed method acquired the best performance compared to other well-known methods. In the future, we will combine our GC attention with other DL-based networks and apply these novel models on other HSI datasets.