Generating a Baseline Map of Surface Fuel Loading Using Stratified Random Sampling Inventory Data through Cokriging and Multiple Linear Regression Methods
Abstract
:1. Introduction
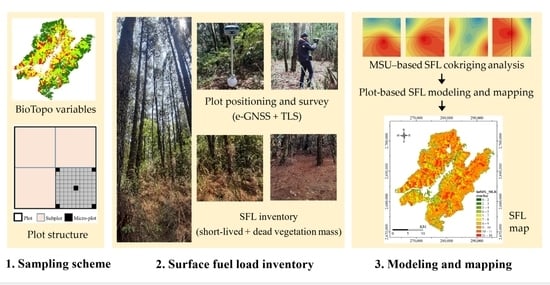
2. Materials and Methods
2.1. Study Site and Data Acquisition
2.2. Surface Fuel Load Inventory Using Stratified Random Sampling and Cokriging Analysis
2.3. Modeling of Surface Fuel Loads Using Multiple Linear Regression
3. Results
3.1. The Derived fSFL Semivariogram Models and Their Performance in Estimating Level-1 Plot Surface Fuel Loads
3.2. The Level-2 Subplot-Based fSFL-BioTopo Models and Their Performance in Generating the fSFL Map of the Whole Forest
3.3. The Level-2 Subplot-Based tSFL-BioTopo Model for Total Surface Fuel Loading Estimation
4. Discussion
4.1. The Uncertainty of Surface Fuel Loading Estimation in fSFL and tSFL Models
4.2. The Dependency of Estimation Bias on the Amount of Surface Fuel Loads
4.3. A Possible Strategy for Improving Surface fuel Load Mapping
4.4. An Examination of the Appropriateness of the Cokriging-Based Surface Fuel Mapping Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Simorangkir, D. Fire use: Is it really the cheaper land preparation method for large-scale plantations? Mitig. Adapt Strat. Glob. Chang. 2007, 12, 147–164. [Google Scholar] [CrossRef]
- Kurtulmuslu, M.; Yazici, E. Management of forest fires through the involvement of local communities in Turkey. In Community-Based Fire Management: Case studies from China, the Gambia, Honduras, India, the Lao People’s Democratic Republic and Turkey, Forest Resources Development Service; Working Paper FFM/2; FAO-Regional Office for Asia and the Pacific: Bangkok, Thailand, 2003; Available online: http://www.fao.org/3/ad348e/ad348e0m.htm (accessed on 22 February 2021).
- van der Werf, G.R.; Randerson, J.T.; Giglio, L.; Collatz, G.J.; Mu, M.; Kasibhatla, P.S.; Morton, D.C.; DeFries, R.S.; Jin, Y.; van Leeuwen, T.T. Global fire emissions and the contribution of deforestation, savanna, forest, agricultural, and peat fires (1997–2009). Atmos. Chem. Phys. 2010, 10, 11707–11735. [Google Scholar] [CrossRef] [Green Version]
- Doyog, N.D.; Lin, C.; Lee, Y.J.; Lumbres, R.I.C.; Daipan, B.P.O.; Bayer, D.C.; Parian, C.P. Diagnosing pristine pine forest development through pansharpened-surface-reflectance Landsat images derived aboveground biomass productivity. Forest Ecol. Manag. 2021, 487, 119011. [Google Scholar] [CrossRef]
- Shi, G.; Yan, H.; Zhang, W.; Dodson, J.; Heijnis, H.; Burrows, M. Rapid warming has resulted in more wildfires in northeastern Australia. Sci. Total Environ. 2021, 771, 144888. [Google Scholar] [CrossRef] [PubMed]
- Short, K.C. Spatial Wildfire Occurrence Data for the United States, 1992–2015. FPA_FOD_20170508, 4th ed.; Forest Service Research Data Archive: Fort Collins, CO, USA, 2017.
- Prichard, S.J.; Povak, N.A.; Kennedy, M.C.; Peterson, D.W. Fuel treatment effectiveness in the context of landform, vegetation, and large, wind-driven wildfires. Ecol. Appl. 2020, 30, e02104. [Google Scholar] [CrossRef] [PubMed]
- Viegas, D. Overview of forest fire propagation research. Fire Saf. Sci. 2011, 10, 95–108. [Google Scholar] [CrossRef]
- Burkle, L.A.; Myers, J.A.; Belote, R.T. Wildfire disturbance and productivity as drivers of plant species diversity across spatial scales. Ecosphere 2015, 6, 202. [Google Scholar] [CrossRef]
- Fernandes, P.M.; Barros, A.M.G.; Pinto, A.; Santos, J.A. Characteristics and controls of extremely large wildfires in the western Mediterranean Basin. J. Geophys. Res. Biogeosci. 2016, 121, 2141–2157. [Google Scholar] [CrossRef]
- Gonalez-Mathiesen, G.; Ruane, S.; March, A. Integrating wildfire risk management and spatial planning—A historical review of two Australian planning systems. Int. J. Disaster Risk Reduct. 2021, 53, 101984. [Google Scholar] [CrossRef]
- Ryan, R.G.; Silver, J.D.; Schofield, R. Air quality and health impact of 2019-20 Black Summer megafires and COVID-19 lockdown in Melbourne and Sydney, Australia. Environ. Pollut. 2021, 274, 116498. [Google Scholar] [CrossRef]
- Martins, F.; Xaud, H.; Dos Santos, J.; Galvão, L. Effects of fire on aboveground forest biomass in the northern Brazilian Amazon. J. Trop. Ecol. 2012, 28, 591–601. [Google Scholar] [CrossRef] [Green Version]
- Murphy, B.P.; Prior, L.D.; Cochrane, M.A.; Williamson, G.J.; Bowman, D.M.J.S. Biomass consumption by surface fires across Earth’s most fire prone continent. Glob. Chang. Biol. 2019, 25, 254–268. [Google Scholar] [CrossRef] [Green Version]
- Keith, H.; Lindenmayer, D.B.; Mackey, B.G.; Blair, D.; Carter, L.; McBurney, L.; Okada, S.; Konishi-Nagano, T. Accounting for Biomass Carbon Stock Change Due to Wildfire in Temperate Forest Landscapes in Australia. PLoS ONE 2014, 9, e107126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aragão, L.E.O.C.; Shimabukuro, Y.E. The incidence of fire in Amazonian forests with implications for REDD. Science 2010, 328, 1275. [Google Scholar] [CrossRef] [PubMed]
- Fitzerald, S.; Berger, C.; Leavell, D. Fire FAQs: What is forest fuel, and what are fuel treatments? In EM9230; Oregon State University Extension Service: Corvallis, OR, USA, 2019. [Google Scholar]
- Sikkink, P.G.; Lutes, D.E.; Keane, R.E. Field Guide for Identifying Fuel Loading Models; Gen. Tech. Rep. RMRS-GTR-225; Fort USDA, Forest Service, Rocky Mountain Research Station: Collins, CO, USA, 2009; 33p.
- Skowronski, N.; Clark, K.; Nelson, R.; Hom, J.; Patterson, M. Remotely sensed measurements of forest structure and fuel loads in the Pinelands of New Jersey. Remote Sens. Environ. 2007, 108, 123–129. [Google Scholar] [CrossRef]
- Lo, C.S.; Lin, C. Growth-competition-based stem diameter and volume modeling for tree-level forest inventory using airborne LiDAR Data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2216–2226. [Google Scholar] [CrossRef]
- Anderson, R.S.; Bolstad, P.V. Estimating aboveground biomass and average annual wood biomass increment with airborne leaf-on and leaf-off lidar in great lakes forest types. North. J. Appl. For. 2013, 30, 16–22. [Google Scholar] [CrossRef]
- Lin, C.; Thomson, G.; Popescu, S.C. An IPCC-compliant rechnique for forest carbon stock assessment using airborne lidar-derived tree metrics and competition index. Remote Sens. 2016, 8, 528. [Google Scholar] [CrossRef] [Green Version]
- Erdody, T.L.; Moskal, L.M. Fusion of LiDAR and imagery for estimating forest canopy fuels. Remote Sens. Environ. 2009, 114, 725–737. [Google Scholar] [CrossRef]
- Skowronski, N.S.; Clar, K.L.; Duveneck, M.; Hom, J. Three-dimensional canopy fuel loading predicted using upward and downward sensing LiDAR systems. Remote Sens. Environ. 2011, 115, 703–714. [Google Scholar] [CrossRef]
- Pesonen, A.; Maltamo, M.; Eerikainen, K.; Packalen, P. Airborne laser scanning based prediction of coarse woody debris volumes in a conservation area. Forest Ecol. Manag. 2008, 255, 3288–3296. [Google Scholar] [CrossRef]
- Beucher, S.; Meyer, F. The morphological approach to segmentation: The watershed transformation. In Mathematical Morphology in Image Processing; Marcel Dekker Inc.: New York, NY, USA, 1993; Volume 34, Chapter 12; pp. 452–464. [Google Scholar]
- Wang, D. A multiscale gradient algorithm for image segmentation using watersheds. Pattern Recogn. 1997, 30, 2043–2052. [Google Scholar] [CrossRef]
- Haris, K.; Efstradiadis, S.N.; Maglaveras, N.; Katsaggelos, A.K. Hybrid image segmentation using watersheds and fast region merging. IEEE T. Image Process 1998, 7, 1684–1699. [Google Scholar] [CrossRef] [Green Version]
- Derivaux, S.; Lefevre, S.; Wemmert, C.; Korczak, J. On machine learning in watershed segmentation. In Proceedings of the IEEE International Workshop on Machine Learning in Signal Processing, Thessaloniki, Greece, 27–29 August 2007; pp. 187–192. [Google Scholar] [CrossRef]
- Lin, C.; Thomson, G.; Lo, C.S.; Yang, M.S. A multi-level morphological active contour algorithm for delineating tree crowns in mountainous forest. Photogram. Eng. Remote Sens. 2011, 77, 241–249. [Google Scholar] [CrossRef]
- Lin, C.Y.; Lin, C.; Chang, C.I. A multilevel slicing based coding method for tree detection. In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS), 2018 IEEE International, Valencia, Spain, 22–27 July 2018; pp. 7524–7527. [Google Scholar]
- Alonso-Rego, C.; Arellano-Pérez, S.; Cabo, C.; Ordoñez, C.; Álvarez-González, J.G.; Díaz-Varela, R.A.; Ruiz-González, A.D. Estimating fuel loads and structural characteristics of shrub communities by using terrestrial laser scanning. Remote Sens. 2020, 12, 3704. [Google Scholar] [CrossRef]
- Stefanidou, A.; Gitas, I.Z.; Korhonen, L.; Georgopoulos, N.; Stavrakoudis, D. Multispectral lidar-based estimation of surface fuel load in a dense coniferous forest. Remote Sens. 2020, 12, 3333. [Google Scholar] [CrossRef]
- García, M.; Danson, F.M.; Riaño, D.; Chuvieco, E.; Ramirez, F.A.; Bandugula, V. Terrestrial laser scanning to estimate plot-level forest canopy fuel properties. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 636–645. [Google Scholar] [CrossRef]
- Rowell, E.; Loudermilk, E.L.; Hawley, C.; Pokswinski, C.; Seielstad, C.; Queen, L.; Q’Brien, J.J.; Hudak, A.T.; Goodrick, S.; Hiers, J.K. Coupling terrestrial laser scanning with 3D fuel biomass sampling for advancing wildland fuels characterization. Forest Ecol. Manag. 2020, 462, 117945. [Google Scholar] [CrossRef]
- Arroyo, L.A.; Pascual, C.; Manzanera, J.A. Fire models and methods to map fuel types: The role of remote sensing. Forest Ecol. Manage. 2008, 256, 1239–1252. [Google Scholar] [CrossRef] [Green Version]
- Popescu, S.C.; Zhao, K.; Neuenschwander, A.; Lin, C. Satellite lidar vs small footprint airborne lidar: Comparing the accuracy of aboveground biomass stimates and forest structure metrics at footprint level. Remote Sens. Environ. 2011, 115, 2786–27987. [Google Scholar] [CrossRef]
- Lin, C. Improved derivation of forest stand canopy height structure using harmonized metrics of full-waveform data. Remote Sens. Environ. 2019, 235, 111436. [Google Scholar] [CrossRef]
- Narine, L.L.; Popescu, S.C.; Malambo, L. Using ICESat-2 to estimate and map forest aboveground biomass: A first example. Remote Sens. 2020, 12, 1824. [Google Scholar] [CrossRef]
- Riaño, D.; Chuvieco, E.; Ustin, S.L.; Salas, F.J.; Rodriguez-Perez, J.R.; Ribeiro, L.M.; Viegas, D.X.; Moreno, J.F.; Fernandez, H. Estimation of shrub height for fuel-type mapping combining airborne LiDAR and simultaneous color infrared ortho imaging. Int. J. Wildland Fire 2007, 16, 341–348. [Google Scholar] [CrossRef] [Green Version]
- Jakubowski, M.K.; Guo, Q.; Collins, B.; Stephens, S.; Kelly, M. Predicting surface fuel models and fuel metrics using lidar and CIR imagery in a dense, mountainous forest. Photogram. Eng. Remote Sens. 2013, 79, 37–49. [Google Scholar] [CrossRef] [Green Version]
- Mutlu, M.; Popescu, S.C.; Stripling, C.; Spencer, T. Mapping surface fuel models using lidar and multispectral data fusion for fire behavior. Remote Sens. Environ. 2008, 112, 274–285. [Google Scholar] [CrossRef]
- García, M.; Riaño, D.; Chuvieco, E.; Salas, J.; Danson, F.M. Multispectral and lidar data fusion for fuel type mapping using support vector machine and decision rules. Remote Sens. Environ. 2011, 115, 1369–1379. [Google Scholar] [CrossRef]
- Cohen, J.D.; Deeming, J.E. The National Fire Danger Rating System: Basic Equations; Rep. No. PSW-82; Pacific Southwest Forest and Range Experiment Station: Berkeley, CA, USA, 1982. [Google Scholar]
- Brown, J.K. Bulk densities of nonuniform surface fuels and their application to fire modeling. For. Sci. 1981, 27, 667–683. [Google Scholar] [CrossRef]
- Lin, C.; Tsogt, K.; Zandraabal, T. A decompositional stand structure analysis for exploring stand dynamics of multiple attributes of a mixed-species forest. Forest Ecol. Manag. 2016, 378, 111–121. [Google Scholar] [CrossRef]
- Stephens, S.L.; Finney, M.A.; Schantz, H. Bulk density and fuel loads of ponderosa pine and white fir forest floors: Impacts of leaf morphology. Northwest Sci. 2004, 78, 93–100. [Google Scholar]
- Lin, C.; Dugarsuren, N. Deriving the spatiotemporal NPP pattern in terrestrial ecosystems of Mongolia using MODIS imagery. Photogram. Eng. Remote Sens. 2015, 81, 587–598. [Google Scholar] [CrossRef]
- Dugarsuren, N.; Lin, C. Temporal variations in phenological events of forests, grasslands and desert steppe ecosystems in Mongolia: A remote sensing approach. Ann. For. Res. 2016, 59, 175–190. [Google Scholar]
- Coates, T.A.; Johnson, A.; Aust, W.M.; Hagan, D.L.; Chow, A.T. Forest composition, fuel loading, and soil chemistry resulting from 50 years of forest management and natural disturbance in two southeastern Coastal Plain watersheds, USA. Forest Ecol. Manag. 2020, 473, 118337. [Google Scholar] [CrossRef]
- Su, H.J. Studies on the climate and vegetation types of the natural forests in Taiwan (II)—Altitudinal vegetation zones in relation to temperature gradient. Q. J. Chin. For. 1984, 17, 57–73. [Google Scholar]
- Battaglia, M.A.; Rocca, M.E.; Rhoades, C.C.; Ryan, M.G. Surface fuel loadings within mulching treatments in Colorado coniferous forests. Forest Ecol. Manag. 2010, 260, 1557–1566. [Google Scholar] [CrossRef]
- Mathews, S. Effect of drying temperature on fuel moisture content measurements. Int. J. Wildland Fire 2010, 19, 800–802. [Google Scholar] [CrossRef]
- Frandsen, W.H.; Andrews, P.L. Fire Behavior in Nonuniform Fuels, USDA Forest Service, Intermountain Forest and Range Experimental Station, Res. Paper INT-232, 1979.
- Deutsch, C.V.; Journel, A.G. Geostatistical Software Library and Users’ Guide; Oxford University Press: New York, NY, USA, 1992; 340p. [Google Scholar]
- Berman, J.D.; Breysse, P.N.; White, R.H.; Waugh, D.W.; Curriero, F.C. Evaluating methods for spatial mapping: Applications for estimating ozone concentrations across the contiguous United States. Environ. Technol. Innov. 2015, 3, 1–10. [Google Scholar] [CrossRef]
- Bright, C.B.; Tudak, A.T.; Meddens, A.J.H.; Hawbaker, T.J.; Briggs, J.S.; Kennedy, R.E. Predictin of forest canopy and surface fuels from lidar and satellite time series data in a bark beetle-affected forest. Forests 2017, 8, 322. [Google Scholar] [CrossRef] [Green Version]
- van Aardt, J.A.; Arthur, M.; Sovkoplas, G.; Swetnam, T.L. Lidar-based estimation of forest floor fuel loads using a novel distributional approach. In Proceedings of the SilviLaser 2011, Tasmania, Australia, 16–20 October 2011; pp. 1–8. [Google Scholar]
- Franke, J.; Barradas, A.C.S.; Borges, M.A.; Costa, M.M.; Dias, P.A.; Hoffmann, A.A.; Filho, J.C.O.; Melchiori, A.E.; Siegert, F. Fuel load mapping in the Brazilian Cerrado in support of fire management. Remote Sens. Environ. 2018, 217, 221–232. [Google Scholar] [CrossRef]
- Prichard, S.J.; Sandberg, D.V.; Ottmar, R.D.; Eberhardt, E.; Andreu, A.; Eagle, P.; Swedin, K. Fuel Characteristics Classification System version 3.0: Technical Documentation; General Technicl Report PNW-GTR-887; Pacific Northwest Research Station: Corvallis, OR, USA, 2013; pp. 39–42.
- Marino, E.; Ranz, P.; Tome, J.L.; Noriega, M.A.; Esteban, J.; Madrigal, J. Generation of high-resolution fuel model maps from discrete airborne laser scanner and Landsat-8 OLI: A low-cost and highly updated methodology for large areas. Remote Sens. Environ. 2016, 187, 267–280. [Google Scholar] [CrossRef]
- Sah, J.P.; Ross, M.S.; Rnyder, J.R.; Koptur, S.; Cooley, H.C. Fuel loads, fire regimes, and post-fire fuel dynamics in Florida Keys pine forests. Int. J. Wildland Fire 2006, 15, 463–478. [Google Scholar] [CrossRef]
- Bechtold, W.A.; Scott, C.T. The Forest Inventory and Analysis Plot Design; Gen. Tech. Rep. SRS-80; U.S. Department of Agriculture, Forest Service, Southern Research Station: Asheville, NC, USA, 2005; pp. 37–52.
- Forest Resources Development Service, Brief on National Forest Inventory, Indonesia. MAR-SFM Working Paper 18. Forestry Department, UN-FAO. 2007; 1–14.
- Lin, C.; Trianingsih, D. Identifying forest ecosystem regions for agricultural use and conservation. Sci. Agric. 2016, 73, 62–70. [Google Scholar] [CrossRef]













| Forest Type | Plot 1 | Plot 2 | Plot 3 | Plot 4 | Plot 5 | Plot 6 | Plot 7 | Plot 8 |
|---|---|---|---|---|---|---|---|---|
| Pine |  |  |  |  |  |  |  |  |
| Model * | Gaus (1) | Exp (2) | Exp (3) | Exp (3) | Exp (4) | Spher (1) | Exp (4) | Exp (4) |
| RMSE | 0.3036 | 0.3158 | 0.1604 | 0.1999 | 0.1762 | 0.1809 | 0.2667 | 0.0902 |
| PRMSE | 26.31 | 28.71 | 15.31 | 20.91 | 16.94 | 19.54 | 27.61 | 4.83 |
| Conifer |  |  |  |  |  |  |  |  |
| Model * | Exp (4) | Exp (4) | Exp (4) | Exp (1) | Exp (1) | Exp (1) | Exp (2) | Exp (4) |
| RMSE | 0.2428 | 0.2594 | 0.2023 | 0.1687 | 0.3012 | 0.1423 | 0.2750 | 0.2387 |
| PRMSE | 32.81 | 31.18 | 18.46 | 29.91 | 43.15 | 22.80 | 39.51 | 35.42 |
| Mixed |  |  |  |  |  |  |  | x |
| Model * | Exp (3) | Exp (5) | Exp (2) | Cir (4) | Exp (4) | Exp (3) | Exp (6) | x |
| RMSE | 0.6082 | 0.7723 | 0.2239 | 0.2777 | 0.4112 | 0.2295 | 0.1988 | x |
| PRMSE | 39.14 | 50.95 | 36.58 | 35.06 | 31.29 | 30.68 | 48.88 | x |
| Broadleaf |  |  |  |  |  |  |  | x |
| Model * | Exp (2) | Exp (4) | Exp (1) | Exp (5) | Exp (4) | Exp (4) | Exp (2) | x |
| RMSE | 0.2229 | 0.1215 | 0.0934 | 0.2685 | 0.1332 | 0.1712 | 0.3411 | x |
| PRMSE | 24.44 | 17.21 | 21.13 | 45.05 | 23.13 | 29.12 | 43.61 | x |
| Forest Type | Subplot ¶ | Plot 1 | Plot 2 | Plot 3 | Plot 4 | Plot 5 | Plot 6 | Plot 7 | Plot 8 | AVG | STD |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pine (n1 = 32) | LL | 149.75 | 132.98 | 75.89 | 161.72 | 121.82 | 63.54 | 92.59 | 79.22 | 107.32 | 24.56 |
| LR | 122.12 | 120.37 | 125.91 | 126.11 | 139.38 | 101.47 | 87.41 | 83.19 | |||
| UL | 139.70 | 120.52 | 73.71 | 119.99 | 82.82 | 84.83 | 86.04 | 109.47 | |||
| UR | 120.34 | 110.68 | 128.56 | 78.36 | 97.3 | 112.78 | 76.40 | 109.42 | |||
| Conifer (n2 = 32) | LL | 89.93 | 90.90 | 113.00 | 91.88 | 76.28 | 55.86 | 66.12 | 60.31 | 81.34 | 22.90 |
| LR | 95.32 | 76.19 | 135.27 | 46.10 | 76.17 | 40.48 | 82.05 | 48.35 | |||
| UL | 93.78 | 85.37 | 110.91 | 68.92 | 99.70 | 82.24 | 90.00 | 92.86 | |||
| UR | 85.60 | 56.18 | 138.06 | 49.73 | 67.62 | 68.18 | 84.53 | 84.99 | |||
| Mixed (n3 = 28) | LL | 86.04 | 223.01 | 104.74 | 87.04 | 225.84 | 73.07 | 36.48 | x | 99.58 | 56.11 |
| LR | 80.86 | 227.40 | 48.80 | 94.39 | 174.59 | 89.64 | 41.86 | x | |||
| UL | 87.53 | 138.60 | 63.41 | 80.39 | 111.58 | 73.27 | 56.27 | x | |||
| UR | 91.69 | 180.47 | 39.15 | 87.23 | 104.04 | 46.44 | 34.30 | x | |||
| Broadleaf (n4 = 28) | LL | 83.50 | 67.42 | 54.91 | 71.69 | 56.90 | 65.14 | 92.40 | x | 73.54 | 16.28 |
| LR | 107.28 | 74.87 | 53.79 | 64.40 | 62.95 | 58.54 | 104.31 | x | |||
| UL | 74.98 | 92.06 | 49.62 | 85.58 | 63.65 | 73.2 | 84.48 | x | |||
| UR | 100.47 | 77.08 | 44.76 | 68.04 | 70.53 | 64.07 | 92.55 | x |
| Forest Type | Subplot ¶ | Plot 1 | Plot 2 | Plot 3 | Plot 4 | Plot 5 | Plot 6 | Plot 7 | Plot 8 | AVG | STD |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pine (n1 = 32) | LL | 149.75 | 145.32 | 75.89 | 161.72 | 125.38 | 70.93 | 92.59 | 109.61 | 114.03 | 24.99 |
| LR | 122.12 | 132.71 | 125.91 | 126.11 | 142.93 | 108.86 | 87.41 | 113.58 | |||
| UL | 139.70 | 132.86 | 73.71 | 119.99 | 86.38 | 92.22 | 86.04 | 139.86 | |||
| UR | 120.34 | 123.02 | 128.56 | 78.36 | 100.86 | 120.17 | 76.40 | 139.81 | |||
| Conifer (n2 = 32) | LL | 89.93 | 90.90 | 113.00 | 91.88 | 77.19 | 55.86 | 66.12 | 114.54 | 88.23 | 26.70 |
| LR | 95.32 | 76.19 | 135.27 | 46.10 | 77.07 | 40.48 | 82.05 | 102.59 | |||
| UL | 93.78 | 85.37 | 110.91 | 68.92 | 100.61 | 82.24 | 90.00 | 147.10 | |||
| UR | 85.60 | 56.18 | 138.06 | 49.73 | 68.53 | 68.18 | 84.53 | 139.22 | |||
| Mixed (n3 = 28) | LL | 90.18 | 224.96 | 104.74 | 87.04 | 226.88 | 83.38 | 37.88 | x | 102.27 | 55.71 |
| LR | 85.00 | 229.36 | 48.80 | 94.39 | 175.62 | 99.94 | 43.26 | x | |||
| UL | 91.67 | 140.55 | 63.41 | 80.39 | 112.61 | 83.58 | 57.67 | x | |||
| UR | 95.83 | 182.43 | 39.15 | 87.23 | 105.08 | 56.75 | 35.70 | x | |||
| Broadleaf (n4 = 28) | LL | 83.50 | 67.42 | 54.91 | 72.18 | 56.90 | 88.72 | 92.40 | x | 76.98 | 16.63 |
| LR | 107.28 | 74.87 | 53.79 | 64.89 | 62.95 | 82.12 | 104.31 | x | |||
| UL | 74.98 | 92.06 | 49.62 | 86.06 | 63.65 | 96.78 | 84.48 | x | |||
| UR | 100.47 | 77.08 | 44.76 | 68.53 | 70.53 | 87.65 | 92.55 | x |
| Model ¶ | fSFL Model R2 | RMSE (kg/m2) | PRMSE (%) | tSFL Model R2 | RMSE (kg/m2) | PRMSE (%) |
|---|---|---|---|---|---|---|
| Equation (4)/Equation (6) | 0.162 (F = 3.096, p < 0.005, n = 120) | 34.10 | 37.59 | 0.144 (F = 2.701, p < 0.013, n = 120) | 35.02 | 36.57 |
| Equation (5)/Equation (7) | 0.173 (F = 8.063, p < 0.001, n = 120) | 33.07 | 38.03 | 0.168 (F = 7.836, p < 0.001, n = 120) | 33.81 | 37.85 |
| DeGroup 1 | 0.154 (F = 2.295, p = 0.034, n = 96) | 23.28 | 28.56 | 0.128 (F = 1.844, p = 0.089, n = 96) | 24.10 | 28.84 |
| DeGroup 2 | 0.167 (F = 2.526, p = 0.020, n = 96) | 25.82 | 33.75 | 0.164 (F = 2.469, p = 0.023, n = 96) | 25.73 | 31.44 |
| DeGroup 3 | 0.182 (F = 2.801, p = 0.011, n = 96) | 46.70 | 46.30 | 0.145 (F = 2.128, p = 0.049, n = 96) | 47.96 | 45.59 |
| DeGroup 4 | 0.136 (F = 1.986, p = 0.066, n = 96) | 39.25 | 37.91 | 0.120 (F = 1.713, p = 0.116, n = 96) | 39.05 | 36.11 |
| DeGroup 5 | 0.193 (F = 3.016, p = 0.007, n = 96) | 37.82 | 41.36 | 0.188 (F = 2.908, p = 0.009, n = 96) | 39.94 | 39.90 |
| DePine | 0.106 (F = 1.352, p = 0.237, n = 88) | 38.47 | 35.84 | 0.051 (F = 0.609, p = 0.747, n = 88) | 37.01 | 32.45 |
| DeConifer | 0.232 (F = 3.455, p = 0.003, n = 88) | 27.82 | 34.20 | 0.240 (F = 3.607, p = 0.002, n = 88) | 30.70 | 34.79 |
| DeMixed | 0.257 (F = 4.160, p = 0.001, n = 92) | 61.56 | 61.82 | 0.246 (F = 5.231, p < 0.001, n = 92) | 63.02 | 61.62 |
| DeBroadleaf | 0.342 (F = 6.242, p < 0.001, n = 92) | 80.11 | 108.94 | 0.258 (F = 4.167, p = 0.001, n = 92) | 78.89 | 102.48 |
| Models | Forest Types | Areas (ha) | Minimum (ton/ha) | Maximum (ton/ha) | Average (ton/ha) | STD (ton/ha) | Total (tons) |
|---|---|---|---|---|---|---|---|
| lnfSFL-BioTopo | Pine | 13,070 | 1.42 | 18.44 | 10.67 | 1.72 | 139,445.59 |
| (Equation (4)) | Conifer | 14,039 | 1.04 | 13.33 | 9.29 | 1.10 | 130,433.75 |
| Mixed | 7001 | 1.02 | 12.90 | 8.22 | 1.53 | 57,555.40 | |
| Broadleaf | 7280 | 0.66 | 13.96 | 7.18 | 2.40 | 52,283.57 | |
| Sum | 41,390 | 0.66 | 18.44 | 9.17 | 2.08 | 379,718.31 | |
| lntSFL-BioTopo | Pine | 13,070 | 1.28 | 11.95 | 9.61 | 1.01 | 125,665.94 |
| (Equation (6)) | Conifer | 14,039 | 1.03 | 11.62 | 8.81 | 1.03 | 123,659.56 |
| Mixed | 7001 | 1.06 | 12.81 | 8.40 | 1.49 | 58,835.28 | |
| Broadleaf | 7280 | 0.76 | 14.32 | 7.71 | 2.25 | 56,147.02 | |
| Sum | 41,390 | 0.76 | 14.32 | 8.80 | 1.55 | 364,307.80 | |
| Difference | Pine | 13,070 | −6.50 | 1.34 | −1.05 | 1.04 | −13,779.65 |
| (fSFL–tSFL) | Conifer | 14,039 | −3.34 | 0.83 | −0.48 | 0.45 | −6774.19 |
| Mix | 7001 | −2.52 | 0.79 | 0.18 | 0.26 | 1279.88 | |
| Broadleaf | 7280 | −2.19 | 1.10 | 0.53 | 0.32 | 3863.45 | |
| Sum | 41,390 | −6.50 | 1.34 | −0.37 | 0.89 | −15,410.51 |
| Template No. | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Locational template and the number of samples (NS) for deriving model ¶ |  |  |  |  |  |  |
| NS = 5@1 m | NS = 5@2 m | NS = 9@2 m | NS = 13@2 m | NS = 25@2 m | NS = 100@1 m | |
| SFL Prediction map |  |  |  |  |  |  |
| Semivariogram model | Exponential | Exponential | Gaussian | Gaussian | Gaussian | Exponential |
| Secondary variables | slope, aspect, fuel bed depth | slope, aspect, fuel bed depth | slope, aspect, fuel bed depth | slope, aspect, fuel bed depth | slope, aspect, fuel bed depth | slope, aspect, fuel bed depth |
| RMSE (kg/m2) | 0.59 | 0.65 | 0.80 | 0.69 | 0.40 | 0.05 |
| PRMSE (%) | 26.58 | 29.71 | 39.05 | 34.34 | 17.54 | 2.30 |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  |
| 0.60/26.85% | 0.59/26.30% | 0.59/26.12% | 0.59/26.35% | 0.72/31.80% | 0.79/35.42% | 0.79/35.42% | 0.89/39.92% |
 |  |  |  |  |  |  |  |
| 5 (CenLL) | 5 (CenLR) | 5 (CenUL) | 5 (CenUR) | 5 (LL) | 5 (LR) | 5 (UL) | 5 (UR) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.; Ma, S.-E.; Huang, L.-P.; Chen, C.-I.; Lin, P.-T.; Yang, Z.-K.; Lin, K.-T. Generating a Baseline Map of Surface Fuel Loading Using Stratified Random Sampling Inventory Data through Cokriging and Multiple Linear Regression Methods. Remote Sens. 2021, 13, 1561. https://doi.org/10.3390/rs13081561
Lin C, Ma S-E, Huang L-P, Chen C-I, Lin P-T, Yang Z-K, Lin K-T. Generating a Baseline Map of Surface Fuel Loading Using Stratified Random Sampling Inventory Data through Cokriging and Multiple Linear Regression Methods. Remote Sensing. 2021; 13(8):1561. https://doi.org/10.3390/rs13081561
Chicago/Turabian StyleLin, Chinsu, Siao-En Ma, Li-Ping Huang, Chung-I Chen, Pei-Ting Lin, Zhih-Kai Yang, and Kuan-Ting Lin. 2021. "Generating a Baseline Map of Surface Fuel Loading Using Stratified Random Sampling Inventory Data through Cokriging and Multiple Linear Regression Methods" Remote Sensing 13, no. 8: 1561. https://doi.org/10.3390/rs13081561
APA StyleLin, C., Ma, S. -E., Huang, L. -P., Chen, C. -I., Lin, P. -T., Yang, Z. -K., & Lin, K. -T. (2021). Generating a Baseline Map of Surface Fuel Loading Using Stratified Random Sampling Inventory Data through Cokriging and Multiple Linear Regression Methods. Remote Sensing, 13(8), 1561. https://doi.org/10.3390/rs13081561