A Most-Unfavorable-Condition Method for Bridge-Damage Detection and Analysis Using PSP-InSAR
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Materials Description
2.2. Method
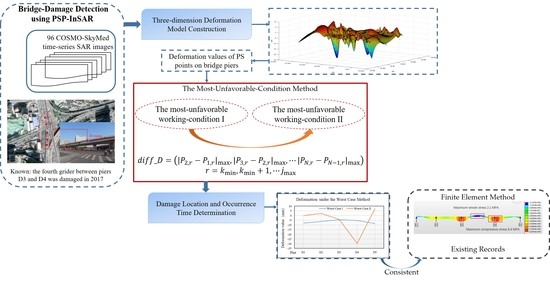
2.2.1. Three-Dimensional Deformation Model Construction
2.2.2. The Most-Unfavorable-Condition Method
- 1.
- The most-unfavorable working-condition I:
- 2.
- The most-unfavorable working condition II:
2.3. Test Design
3. Results
3.1. 3D Deformation Model Construction
3.1.1. Model Construction Method Comparison and Analysis
3.1.2. Three-Dimensional Deformation Model Construction
3.2. The Most-Unfavorable Working-Condition Analysis
- Condition I:
- 2.
- Condition II:
3.3. Damage Detection Using Finite Element Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lanari, R.; Reale, D.; Bonano, M.; Verde, S.; Muhammad, Y.; Fornaro, G.; Casu, F.; Manunta, M. Comment on “Pre-Collapse Space Geodetic Observations of Critical Infrastructure: The Morandi Bridge, Genoa, Italy” by Milillo et al. (2019). Remote Sens. 2020, 12, 4011. [Google Scholar] [CrossRef]
- Milillo, P.; Giardina, G.; Perissin, D.; Milillo, G.; Coletta, A.; Terranova, C. Pre-Collapse Space Geodetic Observations of Critical Infrastructure: The Morandi Bridge, Genoa, Italy. Remote Sens. 2019, 11, 1403. [Google Scholar] [CrossRef] [Green Version]
- Weissgerber, F.; Colin-Koeniguer, E.; Nicolas, J.-M.; Trouvé, N. 3D Monitoring of Buildings Using TerraSAR-X InSAR, DInSAR and PolSAR Capacities. Remote Sens. 2017, 9, 1010. [Google Scholar] [CrossRef] [Green Version]
- The State-of-the-Practice of Modern Structural Health Monitoring for Bridges: A Comprehensive Review. Available online: http://www.mtri.org/bridgecondition/doc/State-of-PracticeSHMforBridges(July2010).pdf (accessed on 3 February 2021).
- Omar, T.; Nehdi, M.L. Remote sensing of concrete bridges decks using unmanned aerial vehicle infrared thermography. Automat. Constr. 2017, 83, 360–371. [Google Scholar] [CrossRef]
- Liu, X.; Wang, P.; Lu, Z.; Gao, K.; Wang, H.; Jiao, C.; Zhang, X. Using terrestrial laser scanning (TLS), Ground-based microwave interferometry, and permanent scatterer interferometry synthetic aperture radar (PS-InSAR). Remote Sens. 2019, 11, 580. [Google Scholar] [CrossRef] [Green Version]
- Alani, A.M.; Aboutalebi, M.; Kilic, G. Applications of ground penetrating radar (GPR) in bridge deck monitoring and assessment. J. Appl. Geophys. 2013, 97, 45–54. [Google Scholar] [CrossRef]
- Meng, X.; Dodson, A.H.; Roberts, G.W. Detecting bridge dynamics with GPS and triaxial accelerometers. Eng. Struct. 2007, 29, 3178–3184. [Google Scholar] [CrossRef]
- Zhang, B.C.; Ding, X.L.; Werner, C.L.; Tan, K.; Zhang, B.; Jiang, M.; Zhao, J.W.; Xu, Y.L. Dynamic Displacement Monitoring of Long-Span Bridges with a Microwave Radar Interferometer. ISPRS J. Photogramm. Remote Sens. 2018, 138, 252–264. [Google Scholar] [CrossRef]
- Lee, J.; Lee, K.C.; Lee, S.; Lee, Y.J.; Sim, S.H. Long-term displacement measurement of bridges using a LiDAR system. Struct. Control Health Monit. 2019, 26, 2428. [Google Scholar] [CrossRef]
- Sousa, J.J.; Bastos, L. Multi-temporal SAR interferometry reveals acceleration of bridge sinking before collapse. Nat. Hazards Earth Syst. Sci. Discuss. 2013, 13, 659–667. [Google Scholar] [CrossRef]
- Sousa, J.J.; Hlavacova, I.; Bakon, M.; Lazecky, M.; Patricio, G.; Guimaraes, P.; Ruiz, A.M.; Bastos, L.; Sousa, A.; Bento, R. Potential of Multi-Temporal InSAR Techniques for Bridges and Dams Monitoring. Procedia Technol. 2014, 16, 834–841. [Google Scholar] [CrossRef] [Green Version]
- Costantini, M.; Falco, S.; Malvarosa, F.; Minati, F. A new method for identification and analysis of persistent scatterers in series of SAR images. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Boston, MA, USA, 7–11 July 2008; Volume 2, pp. 449–452. [Google Scholar]
- Costantini, M.; Falco, S.; Malvarosa, F.; Minati, F.; Trillo, F.; Vecchioli, F. Persistent Scatterer Pair Interferometry: Approach and Application to COSMO-SkyMed SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2869–2879. [Google Scholar] [CrossRef]
- Kireeva, V.I.; Volokhov, E.M.; Lebedev, M.O. Assessment of differential subsidence harmful effects on large bridge structures during the underground space development. E3S Web Conf. 2021, 266, 03003. [Google Scholar] [CrossRef]
- Abdelrahman, A.; Tawfik, M.; El-Saify, A. Investigation on the performance of bridge approach slab. MATEC Web Conf. 2018, 162, 04014. [Google Scholar] [CrossRef] [Green Version]
- Gao, S.; Zhang, C. Construction of Fairing Surface with Polynomial Interpolation. J. Comput.-Aided Des. Comput. Graph. 2008, 6, 759–764. (In Chinese) [Google Scholar]
- Cheng, Y.; Sun, H.Y. Thin Plate Spline Interpolation and Modeling of Height Anomaly of Large Area. Sci. Surv. Mapp. 2008, 4, 42–44. [Google Scholar]
- Wessel, P. A general-purpose Green’s function-based interpolator. Comput. Geosci. 2009, 35, 1247–1254. [Google Scholar] [CrossRef]
- Sandwell, D.T. Biharmonic Spline Interpolation of GEO-3 and SEASAT Altimeter Data. Geophys. Res. Lett. 1987, 14, 139–142. [Google Scholar] [CrossRef] [Green Version]
- Solovyev, S.A. Application of the low-rank approximation technique in the Gauss elimination method for sparse linear systems. A.a.trofimuk Institute of Petroleum Geology & Geophysics. Numer. Methods Program. 2014, 7, 441–460. [Google Scholar]
- Xiang, L.; Ding, Y.; Wei, Z.; Zhang, H.; Li, Z. Research on the Detection Method of Tunnel Surface Flatness Based on Point Cloud Data. Symmetry 2021, 13, 2239. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, K.; Ye, Z.; Liu, C.; Lu, K.; Wang, L. Influence of Temperature on the Natural Vibration Characteristics of Simply Supported Reinforced Concrete Beam. Sensors 2021, 21, 4242. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Wang, Z.; Lin, K.; Sun, Y.; Zhuo, W. Seismic Behavior of a Bridge with New Composite Tall Piers under Near-Fault Ground Motion Conditions. Appl. Sci. 2020, 10, 7377. [Google Scholar] [CrossRef]















| Item | Value |
|---|---|
| Satellite | COSMO-SkyMed |
| Imaging mode | Stripmap |
| Ground resolution | 3 m × 3 m |
| Incident angle | ~20.07° |
| Polarization mode | HH |
| Amount of data | 96 |
| Time span | Sep. 2011~Nov. 2017 |
| Dimension | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| m |
| Fitting Method | Max_Err/mm | SSE/mm2 | R2 |
|---|---|---|---|
| Quadratic polynomial surface interpolation | 11.296 | 4.237 | 0.0177 |
| Thin plate splines interpolation | 6.3394 | 1.655 | 0.6163 |
| Green’s function-based interpolation | 0.33 | 0.185 | 0.9182 |
| No. | D1 | D2 | D3 | D4 | D5 | No. | D1 | D2 | D3 | D4 | D5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 49 | −21.2 | −14.3 | −13 | −26 | −9.3 |
| 2 | −1.3 | 0.1 | 2.68 | 1.28 | 1.3 | 50 | −18.0 | −14.5 | −12.9 | −24.5 | −9 |
| 3 | −2.1 | −1.3 | 1.88 | 1.88 | 0.8 | 51 | −23.0 | −14.1 | −13 | −25 | −10.2 |
| 4 | −1 | −1.5 | 2.18 | 1.48 | 1 | 52 | −22.8 | −16.7 | −13.5 | −26 | −10.9 |
| 5 | −3.24 | −1.9 | −1.65 | 0.98 | 0.7 | 53 | −23.9 | −16.3 | −15.2 | −27.1 | −8.8 |
| 6 | −2.98 | −2.3 | 2.62 | 2.58 | −1.1 | 54 | −23.0 | −16.1 | −14.3 | −28.1 | −8.8 |
| 7 | −4.56 | −1.9 | 1.12 | 2.78 | 0.7 | 55 | −22.7 | −14.7 | −19.2 | −29.5 | 0.6 |
| 8 | −4.8 | −4.6 | 1.42 | 2.78 | 1.2 | 56 | −19.0 | −14.7 | −16.8 | −27.5 | −10.7 |
| 9 | −5.0 | −4.6 | 2.32 | 1.98 | 1.5 | 57 | −27.5 | −16.5 | −21.5 | −28.3 | −9.7 |
| 10 | −4.4 | −2.4 | 1.52 | 1.68 | 1.2 | 58 | −24.8 | −15.2 | −18.8 | −28.4 | −10.5 |
| 11 | −3.9 | −2.2 | 4.22 | 3.37 | 3.1 | 59 | −25.0 | −16.2 | −19.2 | −32.8 | −13.3 |
| 12 | −7.2 | −2.5 | 1.32 | −1.63 | −0.9 | 60 | −27.4 | −19.1 | −22.9 | −35.8 | −13.1 |
| 13 | −7.2 | −2.9 | −2.98 | −4.43 | −8.5 | 61 | −26.1 | −18.6 | −23.6 | −33 | −13.2 |
| 14 | −0.8 | −2 | 2.67 | 1.67 | 6.9 | 62 | −20.0 | −21 | −27.5 | −37.6 | −13.5 |
| 15 | 5.7 | −3.2 | 9.61 | 11.07 | 9.7 | 63 | −28.5 | −22.3 | −26.9 | −37.2 | −13.4 |
| 16 | 1.1 | 2.5 | 2 | 2.27 | 7.2 | 64 | −28.8 | −21.1 | −25.8 | −35.8 | −12.2 |
| 17 | −3.7 | 3.6 | 1.6 | 3.37 | 7.4 | 65 | −29.7 | −20.1 | −29.5 | −36.7 | −14.9 |
| 18 | −7.3 | −5.1 | −2.1 | −5.83 | 4.9 | 66 | −30.9 | −23 | −27.5 | −38.5 | −13.8 |
| 19 | 1.5 | 0.9 | 2.9 | −4.43 | 6 | 67 | −28.2 | −20.9 | −27.7 | −37 | −14.7 |
| 20 | −7.1 | −4.6 | 0.2 | −10.1 | 4.8 | 68 | −29.0 | −23.3 | −27.4 | −39 | −14.8 |
| 21 | −5.9 | 0.6 | 2.1 | −14.1 | 3.1 | 69 | −29.9 | −21.1 | −28.2 | −39.5 | −14.8 |
| 22 | −6.0 | 2.6 | 3.1 | −16.5 | 4.6 | 70 | −28.7 | −19.6 | −26.3 | −39.2 | −16 |
| 23 | −8.2 | 3.1 | 2.2 | −16.1 | 3.6 | 71 | −30.6 | −19.7 | −28.5 | −42 | −16.3 |
| 24 | −6.3 | 0 | 2.2 | −16.3 | 3.7 | 72 | −32.1 | −21.3 | −29 | −46 | −17.9 |
| 24 | −5.4 | 3.8 | 3.3 | −13.7 | 4.7 | 73 | −32.5 | −19.2 | −28.2 | −46.3 | −19.5 |
| 26 | −8.3 | 4.1 | 2.5 | −17 | 4.6 | 74 | −26.0 | −20.2 | −27.5 | −46.6 | −22.4 |
| 27 | −2.3 | 3.7 | −7.2 | −15.6 | 3.8 | 75 | −32.0 | −19.4 | −29.6 | −49.5 | −24.1 |
| 28 | −13.2 | −6.7 | −7.8 | −17.5 | 7.4 | 76 | −28.0 | −17.8 | −27.9 | −50.69 | −23.7 |
| 29 | −14.0 | −6.2 | −8.4 | −20.9 | −1.9 | 77 | −26.0 | −21.8 | −32.2 | −55.1 | −24.2 |
| 30 | −12.1 | −6.2 | −6.5 | −18.4 | 4 | 78 | −28.0 | −21.3 | −35.5 | −53.7 | −24.6 |
| 31 | −10.8 | −4.7 | −7.6 | −17.6 | 4.1 | 79 | −25.0 | −22.8 | −36.1 | −48.7 | −24.9 |
| 32 | −11.8 | −9.3 | −9.9 | −20.6 | 2.7 | 80 | −26.0 | −33.6 | −44.1 | −57.1 | −35 |
| 33 | −13.0 | −8.2 | −8.6 | −19.5 | 3.2 | 81 | −25.9 | −33 | −43.8 | −56.7 | −36.6 |
| 34 | −13.5 | −10.3 | −10.4 | −19.9 | 2.3 | 82 | −26.1 | −33.9 | −42.8 | −60.1 | −37 |
| 35 | −13.3 | −11.9 | −8.7 | −22 | 3.3 | 83 | −35.7 | −34.3 | −41.9 | −60.4 | −37.7 |
| 36 | −13.5 | −11.5 | −8.2 | −20.5 | 2.8 | 84 | −35.2 | −35.1 | −42.7 | −61.7 | −37.8 |
| 37 | −10.9 | −11.9 | −7.6 | −16.7 | 2.7 | 85 | −36.5 | −33.9 | −44.1 | −62.9 | −38.9 |
| 38 | −12.7 | −9.5 | −7.5 | −19.8 | −5.4 | 86 | −36.8 | −33.8 | −43.6 | −63.8 | −39.3 |
| 39 | −18.0 | −15.1 | −12 | −22.3 | −6.8 | 87 | −38.0 | −34.5 | −44.8 | −68.7 | −45.5 |
| 40 | −13.9 | −9.6 | −9.5 | −23.8 | −5.5 | 88 | −43.0 | −39.2 | −47.2 | −71 | −47.1 |
| 41 | −22.6 | −17.5 | −14.7 | −22.9 | −6.3 | 89 | −40.8 | −39.4 | −47 | −70.9 | −46.2 |
| 42 | −21.1 | −13.7 | −10.9 | −21.4 | −5.9 | 90 | −45.7 | −43.5 | −49.8 | −75.53 | −50.3 |
| 43 | −20.7 | −15.1 | −12.5 | −23.4 | −6.4 | 91 | −48.9 | −45.7 | −51.5 | −76.2 | −51.2 |
| 44 | −21.1 | −13.9 | −9.5 | −22.9 | −5.3 | 92 | −44.6 | −40.6 | −48.5 | −70.2 | −47.6 |
| 45 | −18.7 | −9.5 | −8.3 | −23.5 | −3.4 | 93 | −41.4 | −36.5 | −44.3 | −67.9 | −44.6 |
| 46 | −19.7 | −8.6 | −4.8 | −20.1 | −3.1 | 94 | −38.1 | −32.8 | −42.2 | −65.3 | −42 |
| 47 | −20.4 | −12.4 | −11.3 | −23.3 | −7.8 | 95 | −35.7 | −30.7 | −41.6 | −66.4 | −41.9 |
| 48 | −21.0 | −14.9 | −13.1 | −23.2 | −9 | 96 | −35.3 | −31.6 | −40.8 | −66.4 | −40.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Zhang, J.; Liu, X. A Most-Unfavorable-Condition Method for Bridge-Damage Detection and Analysis Using PSP-InSAR. Remote Sens. 2022, 14, 137. https://doi.org/10.3390/rs14010137
Wang R, Zhang J, Liu X. A Most-Unfavorable-Condition Method for Bridge-Damage Detection and Analysis Using PSP-InSAR. Remote Sensing. 2022; 14(1):137. https://doi.org/10.3390/rs14010137
Chicago/Turabian StyleWang, Runjie, Jiameng Zhang, and Xianglei Liu. 2022. "A Most-Unfavorable-Condition Method for Bridge-Damage Detection and Analysis Using PSP-InSAR" Remote Sensing 14, no. 1: 137. https://doi.org/10.3390/rs14010137
APA StyleWang, R., Zhang, J., & Liu, X. (2022). A Most-Unfavorable-Condition Method for Bridge-Damage Detection and Analysis Using PSP-InSAR. Remote Sensing, 14(1), 137. https://doi.org/10.3390/rs14010137