Infrasound Source Localization of Distributed Stations Using Sparse Bayesian Learning and Bayesian Information Fusion
Abstract
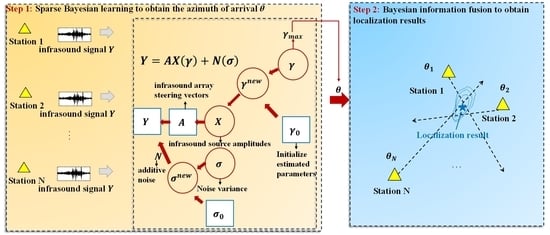
:1. Introduction
- An infrasound source localization method is developed based on the SBL algorithm under the plane wave assumption of infrasound propagation.
- The arrival azimuth estimation results, the uncertainty of the infrasound propagation environment, and the uncertainty of the measurement equipment are fused by the Bayesian information fusion algorithm to obtain the localization, making the infrasound source localization results robust to the actual atmosphere and measurement environment.
- The validity and feasibility of the proposed method are verified using a rocket motor explosion at the Utah Test and Training Range (UTTR).
2. Materials and Methods
2.1. The Tau-p Model for the Infrasound Propagation and Problem Statement
2.1.1. The Tau-p Model for the Infrasound Propagation
2.1.2. Problem Statement for the Infrasound Source Localization
2.2. Estimating the Arrival Azimuth of Infrasound Source Based on the SBL Algorithm
2.2.1. Signal Model for Arrival Azimuth Estimation Based on Plane Wave Assumption
2.2.2. The SBL Algorithm for Infrasound Source Arrival Azimuth Estimation
- (1)
- Stochastic likelihood for the SBL algorithm
- (2)
- Prior (prior distribution) on the infrasound sources
- (3)
- Posterior (posterior distribution) on the infrasound sources
- (4)
- Evidence on the infrasound sources
- (5)
- Infrasound source power estimation using the SBL algorithm
- (6)
- Infrasound source noise variance estimation (hyperparameter )
2.2.3. The Pseudocode for the SBL-Based Estimation Algorithm for Infrasound Arrival Azimuth
| Algorithm 1: The SBL-based infrasound source orientation algorithm |
Input:; |
Output:, ; |
1: initialize: ; |
2: while ; |
3: Compute: |
4: Compute: |
5: |
6: |
7: |
8: is the angle corresponding to |
9: end |
2.3. Bayesian Information Fusion for Infrasound Source Localization
2.3.1. Posteriori Distribution for Infrasound Source Localization
2.3.2. Likelihood Function
2.3.3. The Framework for Infrasound Source Localization
2.4. Technical Flow Chart of the Proposed Infrasound Source Localization Method
3. Results
3.1. Experimetntal Setup
3.2. Arrival Azimuth Estimation Results
3.3. Comparison of the Error of Arrival Azimuth Estimation between SBL Algorithm, FK Analysis, and BF Algorithm
3.4. Bayesian Information Fusion to Obtain Localization Results

4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| p | ray parameter in tau-p model |
| range along the ray direction | |
| the ray characteristic function | |
| transverse offset | |
| the horizontal wind speed along the propagation direction | |
| the maximum height of the infrasound trajectory | |
| the launch elevation angle at the start of the infrasound trajectory | |
| z (axis) | infrasound propagation height |
| angle of wave number vector with x-axis | |
| angle of wave number vector with z-axis | |
| wave number vector | |
| P (function) | the acoustic signal when the initial time is t |
| (vector) | propagation position vector |
| t | initial time |
| infrasound source amplitudes | |
| L | snapshot |
| infrasound signal of L snapshots observed by N infrasound sensors |
| additive noise | |
| N | the number of infrasound sensor |
| the normal distribution sign | |
| infrasound array steering vectors | |
| K | the number of infrasound sources |
| M | number of infrasound planar angle discretizations |
| probability density function | |
| complex Gaussian with noise variance | |
| the diagonal matrix formed by the diagonal elements | |
| the measured infrasound signal | |
| covariance of the posterior distribution on the infrasound source | |
| the infrasound sensor data covariance | |
| the infrasound array data sample covariance matrix (SCM) | |
| Frobenius norm | |
| tr | trace of square matrix |
| Hermitian transpose of the matrix | |
| E | expected value |
| the infrasound array steering vector | |
| 1 norm | |
| stochastic likelihood for the SBL algorithm | |
| posterior on the infrasound sources | |
| prior on the infrasound sources | |
| evidence on the infrasound sources | |
| posterior pdf for the Bayesian information fusion | |
| enables the integration of to be uniform | |
| the prior pdf for the Bayesian information fusion | |
| the likelihood function for the Bayesian information fusion | |
| the variance of azimuth on the random variable at the m-th | |
| snapshot | |
| arrival azimuth estimation | |
| the candidate source location | |
| the variance of the arrival azimuth estimation from the infrasound | |
| measurement equipment | |
| the variance of the arrival azimuth estimation from the infrasound | |
| propagation model |
References
- Le Pichon, A.; Blanc, E.; Hauchecorne, A. Infrasound Monitoring for Atmospheric Studies; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Freret-Lorgeril, V.; Bonadonna, C.; Corradini, S.; Donnadieu, F.; Guerrieri, L.; Lacanna, G.; Marzano, F.S.; Mereu, L.; Merucci, L.; Ripepe, M.; et al. Examples of Multi-Sensor Determination of Eruptive Source Parameters of Explosive Events at Mount Etna. Remote Sens. 2021, 13, 2097. [Google Scholar] [CrossRef]
- Cigna, F.; Tapete, D.; Lu, Z. Remote Sensing of Volcanic Processes and Risk. Remote Sens. 2020, 12, 2567. [Google Scholar] [CrossRef]
- Batubara, M.; Yamamoto, M.-y. Infrasound Observations of Atmospheric Disturbances Due to a Sequence of Explosive Eruptions at Mt. Shinmoedake in Japan on March 2018. Remote Sens. 2020, 12, 728. [Google Scholar] [CrossRef] [Green Version]
- De Angelis, S.; Diaz-Moreno, A.; Zuccarello, L. Recent Developments and Applications of Acoustic Infrasound to Monitor Volcanic Emissions. Remote Sens. 2019, 11, 1302. [Google Scholar] [CrossRef] [Green Version]
- Mutschlecner, J.P.; Whitaker, R.W. Infrasound from earthquakes. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef] [Green Version]
- Garces, M.; Pichon, A.L. Infrasound from Earthquakes, Tsunamis and Volcanoes. In Encyclopedia of Complexity and Systems Science; Springer: New York, NY, USA, 2011; pp. 663–679. [Google Scholar] [CrossRef]
- Laiolo, M.; Ripepe, M.; Cigolini, C.; Coppola, D.; Della Schiava, M.; Genco, R.; Innocenti, L.; Lacanna, G.; Marchetti, E.; Massimetti, F.; et al. Space- and Ground-Based Geophysical Data Tracking of Magma Migration in Shallow Feeding System of Mount Etna Volcano. Remote Sens. 2019, 11, 1182. [Google Scholar] [CrossRef] [Green Version]
- Rost, S.; Thomas, C. Array Seismology: Methods and Applications. Rev. Geophys. 2002, 40, 2-1–2-27. [Google Scholar] [CrossRef] [Green Version]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Wipf, D.; Rao, B. Sparse Bayesian learning for basis selection. IEEE Trans. Signal Process. 2004, 52, 2153–2164. [Google Scholar] [CrossRef]
- Zhang, Z.; Rao, B.D. Sparse Signal Recovery With Temporally Correlated Source Vectors Using Sparse Bayesian Learning. IEEE J. Sel. Top. Signal Process. 2011, 5, 912–926. [Google Scholar] [CrossRef] [Green Version]
- Gerstoft, P.; Mecklenbräuker, C.F.; Xenaki, A.; Nannuru, S. Multisnapshot Sparse Bayesian Learning for DOA. IEEE Signal Process. Lett. 2016, 23, 1469–1473. [Google Scholar] [CrossRef] [Green Version]
- Gemba, K.L.; Nannuru, S.; Gerstoft, P. Robust Ocean Acoustic Localization With Sparse Bayesian Learning. IEEE J. Sel. Top. Signal Process. 2019, 13, 49–60. [Google Scholar] [CrossRef]
- Nannuru, S.; Gemba, K.L.; Gerstoft, P.; Hodgkiss, W.S.; Mecklenbräuker, C.F. Sparse Bayesian learning with multiple dictionaries. Signal Process. 2019, 159, 159–170. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.M.; Huang, Z.T.; Zhou, Y.Y. An Efficient Maximum Likelihood Method for Direction-of-Arrival Estimation via Sparse Bayesian Learning. IEEE Trans. Wirel. Commun. 2012, 11, 1–11. [Google Scholar] [CrossRef]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic Decomposition by Basis Pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef] [Green Version]
- Garcés, M.A.; Hansen, R.A.; Lindquist, K.G. Traveltimes for infrasonic waves propagating in a stratified atmosphere. Geophys. J. Int. 1998, 135, 255–263. [Google Scholar] [CrossRef] [Green Version]
- Modrak, R.T.; Arrowsmith, S.J.; Anderson, D.N. A Bayesian framework for infrasound location. Geophys. J. Int. 2010, 181, 399–405. [Google Scholar] [CrossRef] [Green Version]
- Drob, D.P.; Garcés, M.; Hedlin, M.; Brachet, N. The temporal morphology of infrasound propagation. Pure Appl. Geophys. 2010, 167, 437–453. [Google Scholar] [CrossRef]
- Wipf, D.P.; Rao, B.D. An Empirical Bayesian Strategy for Solving the Simultaneous Sparse Approximation Problem. IEEE Trans. Signal Process. 2007, 55, 3704–3716. [Google Scholar] [CrossRef]
- Bohme, J. Source-parameter estimation by approximate maximum likelihood and nonlinear regression. IEEE J. Ocean. Eng. 1985, 10, 206–212. [Google Scholar] [CrossRef]
- Ji, S.; Xue, Y.; Carin, L. Bayesian Compressive Sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Blom, P.S.; Marcillo, O.; Arrowsmith, S.J. Improved Bayesian Infrasonic Source Localization for regional infrasound. Geophys. J. Int. 2015, 203, 1682–1693. [Google Scholar] [CrossRef] [Green Version]
- Stump, B.; Burlacu, R.; Hayward, C.; Pankow, K.; Nava, S.; Bonner, J.; Hock, S.; Whiteman, D.; Fisher, A.; Kim, T.S. Seismic and Infrasound Energy Generation and Propagation at Local and Regional Distances Phase 1-Divine Strake Experiment; Southern Methodist University: Dallas, TX, USA, 2008. [Google Scholar]
- Arrowsmith, S.J.; Whitaker, R.; Taylor, S.R.; Burlacu, R.; Stump, B.; Hedlin, M.; Randall, G.; Hayward, C.; ReVelle, D. Regional monitoring of infrasound events using multiple arrays: Application to Utah and Washington State. Geophys. J. Int. 2008, 175, 291–300. [Google Scholar] [CrossRef] [Green Version]
- Stump, B.W.; Zhou, R.M.; Kim, T.S.; Chen, Y.T.; Yang, Z.X.; Herrmann, R.B.; Burlacu, R.; Hayward, C.; Pankow, K. Shear Velocity Structure in NE China and Characterization of Infrasound Wave Propagation in the 1–210 km Range; Southern Methodist University: Dallas, TX, USA, 2008. [Google Scholar]
- Capon, J.; Bolt, B. Signal processing and frequency-wavenumber spectrum analysis for a large aperture seismic array. In Methods in Computational Physics; Elsevier: Amsterdam, The Netherlands, 1973; Volume 13, pp. 1–59. [Google Scholar]
- Aki, K.; Richards, P.G. Quantative seismology: Theory and methods. Earth Sci. Rev. 1981, 17, 296–297. [Google Scholar]
- Shani-Kadmiel, S.; Averbuch, G.; Smets, P.; Assink, J.; Evers, L. The 2010 Haiti earthquake revisited: An acoustic intensity map from remote atmospheric infrasound observations. Earth Planet. Sci. Lett. 2021, 560, 116795. [Google Scholar] [CrossRef]
















| Station | Location |
|---|---|
| Source location | 41.1310°N, 112.8950°W |
| BGU | 40.9204°N, 112.0309°W |
| BRP | 39.4727°N, 110.7409°W |
| HWU | 41.6071°N, 111.5652°W |
| WMU | 40.0795°N, 111.8310°W |
| Station Number | Snapshots | Array Aperture | Angular Resolution | Sensor |
|---|---|---|---|---|
| BGU | 39 | 135 m | 0.1 | BGU1, BGU3 |
| BRP | 39 | 150 m | 0.1 | BRP1, BRP3 |
| HWU | 39 | 140 m | 0.1 | HWU1, HWU3 |
| WMU | 39 | 150 m | 0.1 | WMU2, WMU3 |
| Station Number | Arrival Azimuth Estimation Results (°) | Actual Azimuths (°) | Estimation Error (°) |
|---|---|---|---|
| BGU | 32.91 | 31.99 | 0.92 |
| BRP | 307.35 | 307.51 | 0.16 |
| HWU | 252.07 | 250.54 | 1.53 |
| WMU | 314.35 | 314.66 | 0.31 |
| Station Number | SBL Arrival Azimuth Estimation Error (°) | FK Arrival Azimuth Estimation Error (°) | Beamforming Arrival Azimuth Estimation Error (°) |
|---|---|---|---|
| BGU | 0.92 | 2.94 | 3.48 |
| BRP | 0.16 | 4.78 | 3.23 |
| HWU | 1.53 | 2.71 | 4.43 |
| WMU | 0.31 | 9.18 | 1.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Yi, X.; Yu, L.; Zhang, C.; Wang, T.; Zhang, X. Infrasound Source Localization of Distributed Stations Using Sparse Bayesian Learning and Bayesian Information Fusion. Remote Sens. 2022, 14, 3181. https://doi.org/10.3390/rs14133181
Wang R, Yi X, Yu L, Zhang C, Wang T, Zhang X. Infrasound Source Localization of Distributed Stations Using Sparse Bayesian Learning and Bayesian Information Fusion. Remote Sensing. 2022; 14(13):3181. https://doi.org/10.3390/rs14133181
Chicago/Turabian StyleWang, Ran, Xiaoquan Yi, Liang Yu, Chenyu Zhang, Tongdong Wang, and Xiaopeng Zhang. 2022. "Infrasound Source Localization of Distributed Stations Using Sparse Bayesian Learning and Bayesian Information Fusion" Remote Sensing 14, no. 13: 3181. https://doi.org/10.3390/rs14133181
APA StyleWang, R., Yi, X., Yu, L., Zhang, C., Wang, T., & Zhang, X. (2022). Infrasound Source Localization of Distributed Stations Using Sparse Bayesian Learning and Bayesian Information Fusion. Remote Sensing, 14(13), 3181. https://doi.org/10.3390/rs14133181