MIMO Radar Sparse Recovery Imaging with Wideband Interference Prediction
Abstract
:1. Introduction
- (1)
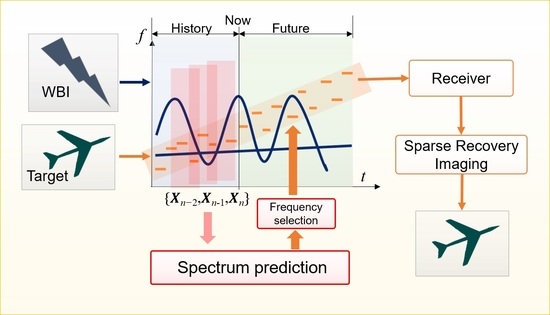
- The DL based method for WBI prediction in the TF domain is proposed. We explore the spatiotemporal correlation of WBI in the TF domain and transform the WBI prediction problem into a spatiotemporal image sequence prediction problem. By using a sliding short-time Fourier transform (STFT) to process the measured WBI to generate a sequence of TF images, the TF images of the WBI in the future are predicted based on a trained DL network.
- (2)
- According to the predicted WBI, we adaptively design the random sparse stepped frequency (RSSF) waveform to make it orthogonal to the future WBI in the TF domain. By doing so, it brings two advantages as follows. Compared to the waveform design method based on historical WBI, the designed waveform with our method can adaptively avoid the WBI in the measurement. Compared to the WBI mitigation method, we can reserve the total information of target signal, since the designed waveform avoid the WBI to the maximum extent. Thus, we can improve the target imaging performance with the proposed method.
- (3)
- Furthermore, we apply the tensor-based smoothed L0 (TSL0) algorithm [22] to reconstruct the 3D high-resolution target image from the sparse received signal cube. With the WBI prediction and due to the advantages of sparse recovery, the proposed imaging method can obtain high effectiveness and robustness in different WBI environments, which are verified by various simulations.
2. Materials and Methods
2.1. Signal Model
2.2. Conventional Imaging Methods
2.2.1. Imaging Method with WDR
2.2.2. Imaging Method with SWD
2.3. Proposed Imaging Method
2.3.1. Framework of Our Method
2.3.2. WBI Prediction via PredRNN
Introduction of PredRNN
Application to WBI Prediction
3. Results
3.1. Prediction Results of Different WBIs
3.2. Imaging Results under Different WBIs
3.3. Robustness of the Proposed Method
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fishler, E.; Haimovich, A.; Blum, R.; Chizhik, D.; Cimini, L.; Valenzuela, R. MIMO radar: An idea whose time has come. In Proceedings of the 2004 IEEE Radar Conference, Philadelphia, PA, USA, 29 April 2004; pp. 71–78. [Google Scholar]
- Bliss, D.W.; Forsythe, K.W. Multiple-input multiple-output (MIMO) radar and imaging: Degrees of freedom and resolution. In Proceedings of the Thirty-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; pp. 54–59. [Google Scholar]
- Ding, S.; Tong, N.; Zhang, Y.; Hu, X. Super-resolution 3D imaging in MIMO radar using spectrum estimation theory. IET Radar Sonar Navig. 2017, 11, 304–312. [Google Scholar] [CrossRef]
- Ding, S.; Tong, N.; Zhang, Y.; Hu, X.; Zhao, X. Cognitive MIMO Imaging Radar Based on Doppler Filtering Waveform Separation. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6929–6944. [Google Scholar] [CrossRef]
- Feng, W.; Friedt, J.-M.; Nico, G.; Sato, M. 3-D Ground-Based Imaging Radar Based on C-Band Cross-MIMO Array and Tensor Compressive Sensing. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1585–1589. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Hu, X.; Tong, N.; Zhang, Y.; Huang, D. MIMO Radar Imaging with Nonorthogonal Waveforms Based on Joint-Block Sparse Recovery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5985–5996. [Google Scholar] [CrossRef]
- Jiao, Z.; Ding, C.; Liang, X.; Chen, L.; Zhang, F. Sparse Bayesian learning based three-dimensional imaging algorithm for off-grid air targets in MIMO radar array. Remote Sens. 2018, 10, 369. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Feng, C.; Wang, Y.; Guo, Y. Adaptive Waveform Optimization for MIMO Radar Imaging Based on Sparse Recovery. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2898–2914. [Google Scholar] [CrossRef]
- Zhou, C.; Li, F.; Li, N.; Zheng, H.; Wang, R.; Wang, X. Improved eigensubspace-based approach for radio frequency interference filtering of synthetic aperture radar images. J. Appl. Remote Sens. 2017, 11, 25004. [Google Scholar] [CrossRef]
- Li, D.; Liu, H.; Yang, L. Efficient time-varying interference suppression method for synthetic aperture radar imaging based on time-frequency reconstruction and mask technique. IET Radar Sonar Navig. 2015, 9, 827–834. [Google Scholar] [CrossRef]
- Tao, M.; Zhou, F.; Zhang, Z. Wideband Interference Mitigation in High-Resolution Airborne Synthetic Aperture Radar Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 74–87. [Google Scholar] [CrossRef]
- Liu, H.; Li, D.; Zhou, Y.; Truong, T.-K. Simultaneous Radio Frequency and Wideband Interference Suppression in SAR Signals via Sparsity Exploitation in Time–Frequency Domain. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5780–5793. [Google Scholar] [CrossRef]
- Ding, Y.; Fan, W.; Tao, M.; Zhang, Z.; Wang, L.; Zhou, F.; Lu, B. Wideband interference mitigation for synthetic aperture radar based on the variational Bayesian method. Signal Process. 2022, 198, 108581. [Google Scholar] [CrossRef]
- Han, W.; Bai, X.; Fan, W.; Wang, L.; Zhou, F. Wideband Interference Suppression for SAR via Instantaneous Frequency Estimation and Regularized Time-Frequency Filtering. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Z.; Xie, R.; Ran, L.; Wang, J. MIMO radar waveform design for target detection in the presence of interference. Digit Signal Process. 2021, 114, 103060. [Google Scholar] [CrossRef]
- Tierney, C.; Mulgrew, B. Adaptive waveform design for interference mitigation in SAR. Signal Process. 2021, 178, 107759. [Google Scholar] [CrossRef]
- Shi, J.; Jiu, B.; Liu, Y.; Yan, J.; Liu, H.; Hu, L. Fast transmit waveform design method for interference mitigation in simultaneous multibeam MIMO scheme. Electron. Lett. 2016, 52, 1166–1168. [Google Scholar] [CrossRef]
- Fan, W.; Zhou, F.; Tao, M.; Bai, X.; Rong, P.; Yang, S.; Tian, T. Interference Mitigation for Synthetic Aperture Radar Based on Deep Residual Network. Remote Sens. 2019, 11, 1654. [Google Scholar] [CrossRef] [Green Version]
- Tao, M.; Li, J.; Su, J.; Wang, L. Characterization and Removal of RFI Artifacts in Radar Data via Model-Constrained Deep Learning Approach. Remote Sens. 2022, 14, 1578. [Google Scholar] [CrossRef]
- Li, W.; Gan, Y.; Zhao, J.; Zou, K.; Zheng, Z. Joint waveform design of cognitive radar based on LSTM network in the presence of signal-dependent interference. J. Appl. Remote. Sens. 2021, 15, 37501. [Google Scholar] [CrossRef]
- Qiu, W.; Zhou, J.; Zhao, H.Z.; Fu, Q. Fast sparse reconstruction algorithm for multidimensional signals. Electron. Lett. 2014, 50, 1583–1585. [Google Scholar] [CrossRef]
- Feng, W.; Yi, L.; Sato, M. Near range radar imaging based on block sparsity and cross-correlation fusion algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2079–2089. [Google Scholar] [CrossRef]
- Shawel, B.S.; Woldegebreal, D.H.; Pollin, S. Convolutional LSTM-based Long-Term Spectrum Prediction for Dynamic Spectrum Access. In Proceedings of the 2019 27th European Signal Processing Conference (EUSIPCO), A Coruna, Spain, 2–6 September 2019; pp. 1–5. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. Predrnn: Recurrent neural networks for predictive learning using spatiotemporal lstms. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 879–888. [Google Scholar]
- Huang, Y.; Zhang, L.; Li, J.; Chen, Z.; Yang, X. Reweighted tensor factorization method for SAR narrowband and wideband interference mitigation using smoothing multiview tensor model. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3298–3313. [Google Scholar] [CrossRef]
- Huang, Y.; Liao, G.; Xiang, Y.; Zhang, Z.; Li, J.; Nehorai, A. Reweighted nuclear norm and reweighted Frobenius norm minimizations for narrowband RFI suppression on SAR system. IEEE Trans. Geosci. Remote Sens. 2019, 11, 5949–5962. [Google Scholar] [CrossRef]














| Parameter | Value Range | Parameter | Value Range |
|---|---|---|---|
| BCM | ISR = [40, 70] dB | BSM | ISR = [40, 70] dB |
| fCM | ±[0, 50] MHz | K | {1, 2, 3} |
| TCM | [15, 20] μs | βk | [200, 500] |
| μ | ±[4, 6] MHz/μs | fk | [0.02, 0.05] MHz |
| fSM | ±[0, 40] MHz | φk | [−π, π] |
| Parameter | Value |
|---|---|
| Tx/Rx antenna number | M = N = 36 |
| Tx/Rx antenna spacing | dt = dr = 8 m |
| Center frequency | fc = 10 GHz |
| Frequency step | Δf = 2 MHz |
| Sub-pulse number | Q = 128 |
| Sub-pulse duration | Ts = 0.5 us |
| WBI | RND Sel. | WDR | SWD | Proposed | |
|---|---|---|---|---|---|
| MSE (dB) | CM-WBI | −5.0816 | −7.8354 | −8.2236 | −8.3893 |
| SM-WBI | 4.8549 | −6.8587 | 4.9389 | −7.6529 | |
| Mixed WBI | 13.7198 | −2.2180 | 3.1501 | −7.0912 | |
| IC | CM-WBI | 132.0076 | 156.2876 | 159.9774 | 159.1816 |
| SM-WBI | 38.0723 | 156.6958 | 38.9409 | 159.3246 | |
| Mixed WBI | 23.5171 | 99.5433 | 47.5641 | 155.4871 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, T.; Tong, N.; Feng, W.; Wan, P.; Hu, X. MIMO Radar Sparse Recovery Imaging with Wideband Interference Prediction. Remote Sens. 2022, 14, 3774. https://doi.org/10.3390/rs14153774
Pu T, Tong N, Feng W, Wan P, Hu X. MIMO Radar Sparse Recovery Imaging with Wideband Interference Prediction. Remote Sensing. 2022; 14(15):3774. https://doi.org/10.3390/rs14153774
Chicago/Turabian StylePu, Tao, Ningning Tong, Weike Feng, Pengcheng Wan, and Xiaowei Hu. 2022. "MIMO Radar Sparse Recovery Imaging with Wideband Interference Prediction" Remote Sensing 14, no. 15: 3774. https://doi.org/10.3390/rs14153774
APA StylePu, T., Tong, N., Feng, W., Wan, P., & Hu, X. (2022). MIMO Radar Sparse Recovery Imaging with Wideband Interference Prediction. Remote Sensing, 14(15), 3774. https://doi.org/10.3390/rs14153774