Impact of Training Set Configurations for Differentiating Plantation Forest Genera with Sentinel-2 Imagery and Machine Learning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Areas
2.2. Data Collection and Preparation
2.2.1. Imagery
2.2.2. In Situ Data
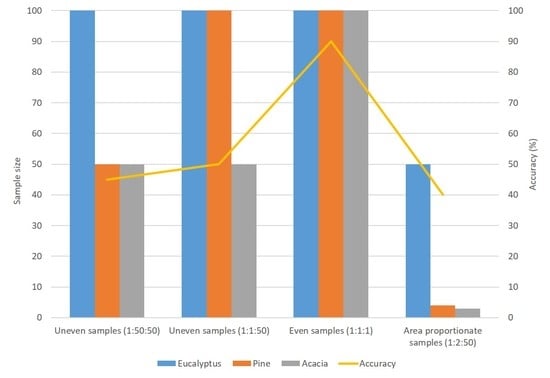
2.3. Experimental Design
- Experiment A1: P-3000, E-3000, and A-3000
- Experiment A2: P-2950, E-2950, and A-2950
- …
- Experiment A60: P-50, E-50, and A-50
- Experiment B1.1: P-3000, E-3000, and A-50
- Experiment B1.2: P-2950, E-2950, and A-50
- …
- Experiment B1.3 60: P-50, E-50, and A-50
- Experiment B2.1: P-3000, E-50, and A-3000
- Experiment B2.2: P-2950, E-50, and A-2950
- …
- Experiment B2.60: P-50, E-50, and A-50
- Experiment B2.1: P-50, E-3000, and A-3000
- Experiment B2.2: P-50, E-2950, and A-2950
- …
- Experiment B2.60: P-50, E-50, and A-50
- Experiment C1.1: P-3000, E-50, and A-50
- Experiment C1.2: P-2950, E-50, and A-50
- …
- Experiment C1.60: P-50, E-50, and A-50
- Experiment C2.1: P-50, E-3000, and A-50
- Experiment C2.2: P-50, E-2950, and A-50
- …
- Experiment C2.60: P-50, E-50, and A-50
- Experiment C3.1: P-50, E-50, and A-3000
- Experiment C3: P-50, E-50, and A-2950
- …
- Experiment C3.60: P-50, E-50, and A-50
- Experiment D1: P-3000, E-240, and A-180
- Experiment D2: P-2950, E-236, and A-177
- …
- Experiment D60: P-50, E-4, and A-3
2.4. Classifier Setup
2.5. Accuracy Assessment
2.6. Spectral Analysis
3. Results
3.1. Genus Spectral Profiles
3.2. Classification
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xulu, S.; Peerbhay, K.Y.; Forests, S.; Gebreslasie, M. Remote sensing of forest health and vitality: A South African perspective. South. For. 2018, 1, 12. [Google Scholar] [CrossRef]
- Poynton, R.J. A Silviculturalmap of Southern Africa. S. Afr. J. Sci. 1971, 67, 58–60. [Google Scholar]
- FP&M SETA. Paper and Pulp Sector; FP&M SETA: Johannesburg, South Africa, 2014. [Google Scholar]
- Steyl, I. Strategic Environmental Assessment for Stream Flow Reduction Activities in South Africa; Department of Water Affairs & Forestry, South Africa: Pretoria, South Africa, 1997; pp. 1–14. [Google Scholar]
- Wicks, T.E.; Smith, G.M.; Curran, P.J. Polygon-based aggregation of remotely sensed data for regional ecological analyses. Int. J. Appl. Earth Obs. Geoinf. 2002, 4, 161–173. [Google Scholar] [CrossRef]
- Scott, D.F.; Prinsloo, F.W.; Moses, G.; Mehlomakulu, M.; Simmers, A.D.A. A Re-Analysis of the South African Catchment Afforestation Experimental Data: Report to the Water Research Commission; WRC: Pretoria, South Africa, 2000. [Google Scholar]
- Savage, M.J.; Odhiambo, G.O.; Mengistu, M.G.; Everson, C.S.; Jarmain, C. Measurement of grassland evaporation using a surface-layer scintillometer. Water SA 2010, 36, 1–8. [Google Scholar] [CrossRef]
- van Wyk, D.B. Some Effects of Afforestation on Streamflow in the Western Cape Province, South Africa. Water SA 1987, 12, 31–36. [Google Scholar]
- Van Der Zel, D.W. Accomplishments and Dynamics of the South African Afforestation Permit System. South Afr. For. J. 1995, 172, 49–58. [Google Scholar] [CrossRef]
- Gush, M.B.; Scott, D.F.; Jewitt, G.P.W.; Schulze, R.E.; Hallowes, L.A.; Görgens, A.H.M. A new approach to modelling streamflow reductions resulting from commercial afforestation in south africa. S. Afr. For. J. 2002, 196, 27–36. [Google Scholar] [CrossRef]
- Clulow, A.D.; Everson, C.S.; Gush, M.B. The Long-Term Impact of Acacia Mearnsii Trees on Evaporation, Streamflow and Groundwater Resources; Water Research Commission Report No. TT505/11; WRC: Pretoria, South Africa, 2011. [Google Scholar]
- FSA. Environmental Guidelines for Commercial Forestry Plantations in South Africa; Forestry South Africa: Johannesburg, South Africa, 2019; pp. 1–130. [Google Scholar]
- Forestry South Africa. Timber Plantation Ownership; Forestry South Africa: Johannesburg, South Africa, 2019. [Google Scholar]
- Schulz, J.; Albert, P.; Behr, H.D.; Caprion, D.; Deneke, H.; Dewitte, S.; Dürr, B.; Fuchs, P.; Gratzki, A.; Hechler, P.; et al. Operational climate monitoring from space: The EUMETSAT satellite application facility on climate monitoring (CM-SAF). Atmos. Chem. Phys. 2009, 9, 1687–1709. [Google Scholar] [CrossRef]
- Jokar Arsanjani, J.; Tayyebi, A.; Vaz, E. GlobeLand30 as an alternative fine-scale global land cover map: Challenges, possibilities, and implications for developing countries. Habitat Int. 2016, 55, 25–31. [Google Scholar] [CrossRef]
- Department of Environmental Affairs. South African National Land-Cover 2018 Report & Accuracy Assessment; Department of Environmental Affairs, South Africa: Pretoria, South Africa, 2019; Volume 4. [Google Scholar]
- Lück, W. Generating Automated Forestry Geoinformation Products From Remotely Sensed Imagery. Master’s Thesis, Stellenbosch Unviersity, Stellenbosch, South Africa, 2018. [Google Scholar]
- Franco-Lopez, H.; Ek, A.R.; Bauer, M.E. Estimation and mapping of forest stand density, volume, and cover type using the k-nearest neighbors method. Remote Sens. Environ. 2001, 77, 251–274. [Google Scholar] [CrossRef]
- Stabach, J.A.; Dabek, L.; Jensen, R.; Wang, Y.Q. Discrimination of dominant forest types for Matschie’s tree kangaroo conservation in Papua New Guinea using high-resolution remote sensing data. Int. J. Remote Sens. 2009, 30, 405–422. [Google Scholar] [CrossRef]
- Cho, M.A.; Malahlela, O.; Ramoelo, A. Assessing the utility WorldView-2 imagery for tree species mapping in South African subtropical humid forest and the conservation implications: Dukuduku forest patch as case study. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 349–357. [Google Scholar] [CrossRef]
- Francois, A.; Leckie, D.G. Francios The individual tree crown approach to Ikonos images of a Coniferous Plantation Area. In Photogrammetric Engineering & Remote Sensing; American Society for Photogrammetry and Remote Sensing: Victoria, Canada, 2006. [Google Scholar]
- Immitzer, M.; Atzberger, C.; Koukal, T. Tree species classification with Random forest using very high spatial resolution 8-band worldView-2 satellite data. Remote Sens. 2012, 4, 2661–2693. [Google Scholar] [CrossRef]
- Ke, Y.; Quackenbush, L.J.; Im, J. Remote Sensing of Environment Synergistic use of QuickBird multispectral imagery and LIDAR data for object-based forest species classi fi cation. Remote Sens. Environ. 2010, 114, 1141–1154. [Google Scholar] [CrossRef]
- Pu, R.; Landry, S. A comparative analysis of high spatial resolution IKONOS and WorldView-2 imagery for mapping urban tree species. Remote Sens. Environ. 2012, 124, 516–533. [Google Scholar] [CrossRef]
- Franklin, S.E.; Ahmed, O.S.; Williams, G. Northern Conifer Forest Species Classification Using Multispectral Data Acquired from an Unmanned Aerial Vehicle. Photogramm. Eng. Remote Sens. 2017, 83, 501–507. [Google Scholar] [CrossRef]
- Franklin, S.E.; Ahmed, O.S. Deciduous tree species classification using object-based analysis and machine learning with unmanned aerial vehicle multispectral data. Int. J. Remote Sens. 2018, 39, 5236–5245. [Google Scholar] [CrossRef]
- Buddenbaum, H.; Schlerf, M.; Hill, J. Classification of coniferous tree species and age classes using hyperspectral data and geostatistical methods. Int. J. Remote Sens. 2005, 26, 5453–5465. [Google Scholar] [CrossRef]
- Bujang, M.A.; Baharum, N. Guidelines of the minimum sample size requirements for Cohen’ s Kappa. Epidemiol. Biostat. Public Health 2017, 17, e12267. [Google Scholar]
- Fagan, M.E.; DeFries, R.S.; Sesnie, S.E.; Arroyo-Mora, J.P.; Soto, C.; Singh, A.; Townsend, P.A.; Chazdon, R.L. Mapping species composition of forests and tree plantations in northeastern Costa Rica with an integration of hyperspectral and multitemporal landsat imagery. Remote Sens. 2015, 7, 5660–5696. [Google Scholar] [CrossRef]
- Peerbhay, K.Y.; Mutanga, O.; Ismail, R. Commercial tree species discrimination using airborne AISA Eagle hyperspectral imagery and partial least squares discriminant analysis (PLS-DA) in KwaZulu-Natal, South Africa. ISPRS J. Photogramm. Remote Sens. 2013, 79, 19–28. [Google Scholar] [CrossRef]
- Voss, M.; Sugumaran, R. Seasonal effect on tree species classification in an urban environment using hyperspectral data, LiDAR, and an object-oriented approach. Sensors 2008, 8, 3020–3036. [Google Scholar] [CrossRef] [PubMed]
- Nomura, K.; Mitchard, E.T.A. More than meets the eye: Using Sentinel-2 to map small plantations in complex forest landscapes. Remote Sens. 2018, 10, 1693. [Google Scholar] [CrossRef]
- Mngadi, M.; Odindi, J.; Peerbhay, K.; Mutanga, O. Examining the effectiveness of Sentinel-1 and 2 imagery for commercial forest species mapping. Geocarto Int. 2019, 36, 1–12. [Google Scholar] [CrossRef]
- Vaglio Laurin, G.; Puletti, N.; Hawthorne, W.; Liesenberg, V.; Corona, P.; Papale, D.; Chen, Q.; Valentini, R. Discrimination of tropical forest types, dominant species, and mapping of functional guilds by hyperspectral and simulated multispectral Sentinel-2 data. Remote Sens. Environ. 2016, 176, 163–176. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, J.; Gong, J. Urban flood mapping based on unmanned aerial vehicle remote sensing and random forest classifier-A case of yuyao, China. Water 2015, 7, 1437–1455. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Lukas, V.; Novák, J.; Neudert, L.; Svobodova, I.; Rodriguez-Moreno, F.; Edrees, M.; Kren, J. The combination of UAV survey and Landsat imagery for monitoring of crop vigor in precision agriculture. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 953–957. [Google Scholar] [CrossRef]
- Loggenberg, K.; Strever, A.; Greyling, B.; Poona, N. Modelling water stress in a Shiraz vineyard using hyperspectral imaging and machine learning. Remote Sens. 2018, 10, 202. [Google Scholar] [CrossRef]
- Ma, W.; Gong, C.; Hu, Y.; Meng, P.; Xu, F. The Hughes phenomenon in hyperspectral classification based on the ground spectrum of grasslands in the region around Qinghai Lake. In International Symposium on Photoelectronic Detection and Imaging 2013: Imaging Spectrometer Technologies and Applications; SPIE: Bellingham, DC, USA, 2013; Volume 8910, pp. 363–373. [Google Scholar]
- Belgiu, M.; Dragut, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data, 3rd ed.; Assessing the Accuracy of Remotely Sensed Data; Taylor & Francis Group: London, UK, 2019; pp. 87–106. [Google Scholar]
- Mather, P.M. Computer Processing of Remotely-Sensed Images, 3rd ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Thanh Noi, P.; Kappas, M. Comparison of Random Forest, k-Nearest Neighbor, and Support Vector Machine Classifiers for Land Cover Classification Using Sentinel-2 Imagery. Sensors 2017, 18, 18. [Google Scholar] [CrossRef] [PubMed]
- Foody, G.M. Sample size determination for image classification accuracy assessment and comparison. Int. J. Remote Sens. 2009, 30, 5273–5291. [Google Scholar] [CrossRef]
- Foody, G.M.; Mathur, A.; Sanchez-Hernandez, C.; Boyd, D.S. Training set size requirements for the classification of a specific class. Remote Sens. Environ. 2006, 104, 1–14. [Google Scholar] [CrossRef]
- Dalponte, M.; Ørka, H.O.; Gobakken, T.; Gianelle, D.; Næsset, E. Tree species classification in boreal forests with hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2632–2645. [Google Scholar] [CrossRef]
- Millard, K.; Richardson, M. On the importance of training data sample selection in Random Forest image classification: A case study in peatland ecosystem mapping. Remote Sens. 2015, 7, 8489–8515. [Google Scholar] [CrossRef]
- Mellor, A.; Boukir, S.; Haywood, A.; Jones, S. Exploring issues of training data imbalance and mislabelling on random forest performance for large area land cover classification using the ensemble margin. ISPRS J. Photogramm. Remote Sens. 2015, 105, 155–168. [Google Scholar] [CrossRef]
- Colditz, R.R. An evaluation of different training sample allocation schemes for discrete and continuous land cover classification using decision tree-based algorithms. Remote Sens. 2015, 7, 9655–9681. [Google Scholar] [CrossRef]
- Kraaij, T.; Baard, J.A.; Arndt, J.; Vhengani, L.; van Wilgen, B.W. An assessment of climate, weather, and fuel factors influencing a large, destructive wildfire in the Knysna region. S. Afr. Fire Ecol. 2018, 14, 4. [Google Scholar] [CrossRef]
- ESA. ESA’s Optical High-Resolution Mission for GMES Operational Services; ESA: Paris, France, 2015; 88p. [Google Scholar]
- Fuller, J.A.; Perrin, M.R. Habitat assessment of small mammals in the Umvoti Vlei conservancy, KwaZulu-Natal, South Africa. Afr. J. Wildl. Res. 2001, 31, 1–12. [Google Scholar]
- Breiman, L. Random forests. Mach Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Budei, B.C.; St-Onge, B.; Hopkinson, C.; Audet, F.A. Identifying the genus or species of individual trees using a three-wavelength airborne lidar system. Remote Sens. Environ. 2018, 204, 632–647. [Google Scholar] [CrossRef]
- Pontius, R.G.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Homayouni, S.; Gill, E. The first wetland inventory map of newfoundland at a spatial resolution of 10 m using sentinel-1 and sentinel-2 data on the Google Earth Engine cloud computing platform. Remote Sens. 2019, 11, 43. [Google Scholar] [CrossRef]
- Manna, S.; Raychaudhuri, B. Mapping distribution of Sundarban mangroves using Sentinel-2 data and new spectral metric for detecting their health condition. Geocarto Int. 2020, 35, 434–452. [Google Scholar] [CrossRef]
- Shetty, S. Analysis of Machine Learning Classifiers for LULC Classification on Google Earth Engine Analysis of Machine Learning Classifiers for LULC Classification on Google Earth Engine. Masters Thesis, University of Twente, Twente, The Nerthelands, 2019; pp. 1–65. [Google Scholar]
- Myburgh, G.; Van Niekerk, A. Impact of training set size on object-based land cover classification: A comparison of three classifiers. Int. J. Appl. Geospatial. Res. 2014, 5, 49–67. [Google Scholar] [CrossRef]
- Heydari, S.S.; Mountrakis, G. Effect of classifier selection, reference sample size, reference class distribution and scene heterogeneity in per-pixel classification accuracy using 26 Landsat sites. Remote Sens. Environ. 2018, 204, 648–658. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Viera, A.J.; Garrett, J.M. Understanding interobserver agreement: The kappa statistic. Fam. Med. 2005, 37, 360–363. Available online: http://www1.cs.columbia.edu/~julia/courses/CS6998/Interrater_agreement.Kappa_statistic.pdf (accessed on 4 April 2022). [PubMed]







| Sample Size | Effect on the Overall Accuracy | Author |
|---|---|---|
| The number of samples must be larger than the number of features | Improves accuracy | Belgiu and Dragut [40] |
| The number of samples must = 50 when the number of features = 12 and the area is smaller than 1 million hectares | Improves accuracy | Congalton and Green [41] |
| Must use 10n to 30n training samples, where n is the number of features | Improves accuracy | Mather [42] |
| Increase the number of samples as much as possible | Improves accuracy | Thanh, Noi and Kappas [43] |
| Must not increase the samples too much, as a saturation point exists | No value is added by increasing the samples beyond the saturation point | Foody [44] |
| Must use samples that maximizes interclass and minimizes intraclass separability | Improves accuracy | Foody et al. [45] |
| Unbalanced training sets | The class with the most samples is favoured in the classification | Dalponte et al. [46] |
| Unbalanced training sets | The class with the most samples is favoured in the classification | Millard and Richardson [47] |
| Unbalanced training sets | Improves the classification accuracy of complex classes | Mellor [48] |
| Larger balanced training sets for larger areas | Improves accuracy | Colditz [49] |
| Area-proportional samples | Improves the accuracy of the smallest class being mapped | Belgiu and Dragut [40] |
| Bands | Textural Measures | |
|---|---|---|
| B1—coastal aerosol | Angular second moment | Maximum correlation coefficient |
| B2—blue | Contrast | Cluster prominence |
| B3—green | Correlation | Sum average |
| B4—red | Difference entropy | Sum entropy |
| B5, B6, B7, B8A—vegetation red edge | Entropy | Cluster shade |
| B8—NIR | Inverse difference moment | Sum variance |
| B9—water vapour | Information measure of correlation 1 | Variance |
| B10—SWIR—cirrus | Information measure of correlation 2 | |
| B11, B12—SWIR | Inertia | |
| Vegetation Indices | ||
| NDVI | ||
| EVI | ||
| Study Area 1 (WC) | Study Area 2 (KZN) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Genus | Age (Mean) | Age (Std Dev) | Area (ha) | Area (%) | # | Age (Mean) | Age (Std Dev) | Area (ha) | Area (%) | # |
| Acacia | 35.94 | 12.61 | 118.14 | 3.56 | 40 | 8.75 | 7.10 | 3869.7 | 33.33 | 406 |
| Eucalyptus | 43.18 | 20.49 | 145.79 | 4.40 | 50 | 6.52 | 4.57 | 3869.4 | 33.33 | 718 |
| Pinus | 9.97 | 11.08 | 3052.81 | 92.04 | 940 | 8.78 | 6.50 | 3869.3 | 33.33 | 478 |
| Total | 3316.74 | 1030 | 11,608.4 | 1602 | ||||||
| Acacia vs. Eucalyptus | Acacia vs. Pinus | Eucalyptus vs. Pinus | ||||
|---|---|---|---|---|---|---|
| WC | KZN | WC | KZN | WC | KZ N | |
| Sentinel-2 bands | 0.01615204 | 0.027278119 | 0.01083795 | 0.001678353 | 0.0427256 | 0.041993623 |
| Sentinel-2 bands and vegetation indices | 0.02963264 | 0.017471886 | 0.01521441 | 0.002094672 | 0.08139061 | 0.031343328 |
| Sentinel-2 bands, vegetation indices, and textural features | 0.1258648 | 0.2534354 | 0.2615191 | 0.0000066 | 0.578058 | 0.2554823 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Higgs, C.; van Niekerk, A. Impact of Training Set Configurations for Differentiating Plantation Forest Genera with Sentinel-2 Imagery and Machine Learning. Remote Sens. 2022, 14, 3992. https://doi.org/10.3390/rs14163992
Higgs C, van Niekerk A. Impact of Training Set Configurations for Differentiating Plantation Forest Genera with Sentinel-2 Imagery and Machine Learning. Remote Sensing. 2022; 14(16):3992. https://doi.org/10.3390/rs14163992
Chicago/Turabian StyleHiggs, Caley, and Adriaan van Niekerk. 2022. "Impact of Training Set Configurations for Differentiating Plantation Forest Genera with Sentinel-2 Imagery and Machine Learning" Remote Sensing 14, no. 16: 3992. https://doi.org/10.3390/rs14163992
APA StyleHiggs, C., & van Niekerk, A. (2022). Impact of Training Set Configurations for Differentiating Plantation Forest Genera with Sentinel-2 Imagery and Machine Learning. Remote Sensing, 14(16), 3992. https://doi.org/10.3390/rs14163992