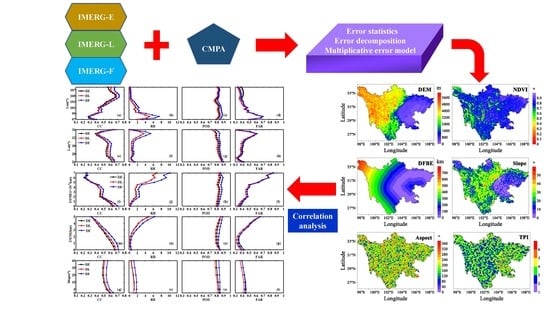
Spatial Patterns of Errors in GPM IMERG Summer Precipitation Estimates and Their Connections to Geographical Features in Complex Topographical Area
Abstract
:1. Introduction
- (1)
- Most studies use conventional statistical metrics to evaluate the overall performance of IMERG estimates, and ultimately attribute the errors to the features such as precipitation intensity and mechanism, solid precipitation, and high altitude [13,14,15,16,17]. However, this research seldom systematically analyzes the error sources and investigates the relationships between the characteristics of errors and the distributions of geographical features.
- (2)
- Some existing studies have proved that the data quality of IMERG varies greatly in different regions and seasons, and the lack of accuracy problem arises in IMERG summer precipitation estimates over the high latitude and elevation regions [5,16,18,19,20,21]. However, few studies have been carried out on the errors of IMERG summer estimates in Sichuan Province, which is one representative of the complex topographical areas and an ideal model for studying the influence of topography on precipitation.
- (3)
- Many studies have reported some potential influence factors of precipitation observation, such as complex precipitation mechanism [13], high elevation [15], high latitude [22], multiple-phase precipitation [14], complex topography [23], temperature [24], bodies of water [5], and so on. At the same time, it should be noted that topographical conditions have been shown to prominently affect the quality of remote sensing data [5,23,25,26,27,28,29,30]. Regrettably, the varieties of geographical features considered in this type of research are very limited.
2. Study Area and Data Sets
2.1. Study Area
2.2. Data Sets
2.2.1. GPM IMERG Precipitation Estimates
2.2.2. Ground Reference Data Sets
2.2.3. Topographical Data Sets
3. Methodologies
3.1. Traditional Statistical Error Metrics
3.2. Independent Error Components
3.3. Systematic and Random Errors
3.4. Regression Analysis
4. Results
4.1. Traditional Statistical Error Metrics
4.2. Independent Error Components
4.3. Systematic and Random Errors
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, S.; Zhou, T. Observed trends in the timing of wet and dry season in China and the associated changes in frequency and duration of daily precipitation. Int. J. Climatol. 2015, 35, 4631–4641. [Google Scholar] [CrossRef]
- Sadeghi, M.; Asanjan, A.A.; Faridzad, M.; Nguyen, P.; Hsu, K.; Sorooshian, S.; Braithwaite, D. PERSIANN-CNN: Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks–Convolutional Neural Networks. J. Hydrometeorol. 2019, 20, 2273–2289. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.P.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Li, N.; Wang, Z.; Sun, K.; Chu, Z.; Leng, L.; Lv, X. A Quality Control Method of Ground-Based Weather Radar Data Based on Statistics. IEEE Trans. Geosci. Remote Sens. 2017, 56, 2211–2219. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Lu, X.; Wei, M.; Tang, G.; Zhang, Y. Evaluation and correction of the TRMM 3B43V7 and GPM 3IMERGM satellite precipitation products by use of ground-based data over Xinjiang, China. Environ. Earth Sci. 2018, 77, 209. [Google Scholar] [CrossRef]
- Arkin, P.A.; Xie, P. The global precipitation climatology project: First algorithm intercomparison project. Bull. Am. Meteorol. Soc. 1994, 75, 401–420. [Google Scholar] [CrossRef]
- Hsu, K.-l.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. Climatol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Joyce, R.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K. Global precipitation map using satellite-borne microwave radiometers by the GSMaP project: Production and validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.-H. NASA global precipitation measurement (GPM) integrated multi-satellite retrievals for GPM (IMERG). Algorithm Theor. Basis Doc. 2015, 4, 26. [Google Scholar]
- Kummerow, C.D.; Barnes, W.L.; Kozu, T.; Shiue, J.; Simpson, J. The Tropical Rainfall Measuring Mission (TRMM) Sensor Package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Panegrossi, G.; Rysman, J.-F.; Casella, D.; Marra, A.C.; Sanò, P.; Kulie, M.S. CloudSat-based assessment of GPM Microwave Imager snowfall observation capabilities. Remote Sens. 2017, 9, 1263. [Google Scholar] [CrossRef]
- Tong, K.; Su, F.; Yang, D.; Hao, Z. Evaluation of satellite precipitation retrievals and their potential utilities in hydrologic modeling over the Tibetan Plateau. J. Hydrol. 2014, 519, 423–437. [Google Scholar] [CrossRef]
- Hosseini-Moghari, S.-M.; Tang, Q. Validation of GPM IMERG V05 and V06 precipitation products over Iran. J. Hydrometeorol. 2020, 21, 1011–1037. [Google Scholar] [CrossRef]
- Zhou, C.; Gao, W.; Hu, J.; Du, L.; Du, L. Capability of imerg v6 early, late, and final precipitation products for monitoring extreme precipitation events. Remote Sens. 2021, 13, 689. [Google Scholar] [CrossRef]
- Chen, F.; Li, X. Evaluation of IMERG and TRMM 3B43 monthly precipitation products over mainland China. Remote Sens. 2016, 8, 472. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.; Ndayisaba, F.; Liu, T.; Kurban, A.; De Maeyer, P. Systematical Evaluation of Satellite Precipitation Estimates Over Central Asia Using an Improved Error-Component Procedure. J. Geophys. Res. Atmos. 2017, 122, 10906–10927. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, X.; Shao, H.; Chen, S.; Liu, T.; Chen, C.; Ding, Q.; Du, H. Evaluation and Intercomparison of High-Resolution Satellite Precipitation Estimates—GPM, TRMM, and CMORPH in the Tianshan Mountain Area. Remote Sens. 2018, 10, 1543. [Google Scholar] [CrossRef]
- Tang, S.; Li, R.; He, J.; Wang, H.; Fan, X.; Yao, S. Comparative Evaluation of the GPM IMERG Early, Late, and Final Hourly Precipitation Products Using the CMPA Data over Sichuan Basin of China. Water 2020, 12, 554. [Google Scholar] [CrossRef] [Green Version]
- Yong, B.; Chen, B.; Gourley, J.J.; Ren, L.; Hong, Y.; Chen, X.; Wang, W.; Chen, S.; Gong, L. Intercomparison of the Version-6 and Version-7 TMPA precipitation products over high and low latitudes basins with independent gauge networks: Is the newer version better in both real-time and post-real-time analysis for water resources and hydrologic extremes? J. Hydrol. 2014, 508, 77–87. [Google Scholar] [CrossRef]
- Iguchi, T.; Kozu, T.; Kwiatkowski, J.; Meneghini, R.; Awaka, J.; Okamoto, K.i. Uncertainties in the rain profiling algorithm for the TRMM precipitation radar. J. Meteorol. Soc. Japan. Ser. II 2009, 87, 1–30. [Google Scholar] [CrossRef]
- Ombadi, M.; Nguyen, P.; Sorooshian, S.; Hsu, K.-l. How much information on precipitation is contained in satellite infrared imagery? Atmos. Res. 2021, 256, 105578. [Google Scholar] [CrossRef]
- Liu, B.; Wan, W.; Xie, H.; Li, H.; Zhu, S.; Zhang, G.; Wen, L.; Hong, Y. A long-term dataset of lake surface water temperature over the Tibetan Plateau derived from AVHRR 1981–2015. Sci. Data 2019, 6, 48. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Shi, Z.; Zhou, Y.; Xu, J.; Yu, W.; Yang, Y. A spatial data mining algorithm for downscaling TMPA 3B43 V7 data over the Qinghai–Tibet Plateau with the effects of systematic anomalies removed. Remote Sens. Environ. 2017, 200, 378–395. [Google Scholar] [CrossRef]
- Zhu, S.; Wan, W.; Xie, H.; Liu, B.; Li, H.; Hong, Y. An efficient and effective approach for georeferencing AVHRR and GaoFen-1 imageries using inland water bodies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2491–2500. [Google Scholar] [CrossRef]
- Wang, X.; Ding, Y.; Zhao, C.; Wang, J. Similarities and improvements of GPM IMERG upon TRMM 3B42 precipitation product under complex topographic and climatic conditions over Hexi region, Northeastern Tibetan Plateau. Atmos. Res. 2019, 218, 347–363. [Google Scholar] [CrossRef]
- Yang, M.; Liu, G.; Chen, T.; Chen, Y.; Xia, C. Evaluation of GPM IMERG precipitation products with the point rain gauge records over Sichuan, China. Atmos. Res. 2020, 246, 105101. [Google Scholar] [CrossRef]
- Zhu, S.; Shen, Y.; Ma, Z. A New Perspective for Charactering the Spatio-temporal Patterns of the Error in GPM IMERG Over Mainland China. Earth Space Sci. 2021, 8, 16. [Google Scholar] [CrossRef]
- Dan, C.; Changyan, Z.; Guangming, X.; Mengyu, D. Characteristics of Climate Change of Summer Rainstorm in Sichuan Basin in the Last 53 Years. Plateau Meteorol. 2018, 37, 197–206. [Google Scholar]
- Yu, L.; Chao, C.; Jia, L.; LI, X.-l.; Rong, Y. Characteristics and causes of regional extreme precipitation events in summer over Sichuan Basin. J. Southwest Univ. 2019, 41, 128–138. [Google Scholar]
- Zhou, Q.; Kang, L.; Jiang, X.; Liu, Y. Relationship between heavy rainfall and altitude in mountainous areas of Sichuan basin. Meteorol. Monogr. 2019, 45, 811–819. [Google Scholar] [CrossRef]
- Shen, P.F.; Zhang, Y.C. Numerical Simulation of Diurnal Variation of Summer Precipitation in Sichuan Basin. Plateau Meteorol. 2011, 30, 860–868. [Google Scholar]
- Sungmin, O.; Foelsche, U.; Kirchengast, G.; Fuchsberger, J.; Tan, J.; Petersen, W.A. Evaluation of GPM IMERG Early, Late, and Final rainfall estimates using WegenerNet gauge data in southeastern Austria. Hydrol. Earth Syst. Sci. 2017, 21, 6559–6572. [Google Scholar] [CrossRef]
- Shen, Y.; Zhao, P.; Pan, Y.; Yu, J. A high spatiotemporal gauge-satellite merged precipitation analysis over China. J. Geophys. Res. 2014, 119, 3063–3075. [Google Scholar] [CrossRef]
- Su, J.; Lü, H.; Crow, W.T.; Zhu, Y.; Cui, Y. The effect of spatiotemporal resolution degradation on the accuracy of IMERG products over the Huai River basin. J. Hydrometeorol. 2020, 21, 1073–1088. [Google Scholar] [CrossRef]
- Su, J.; Lu, H.; Zhu, Y.; Wang, X.; Wei, G. Component Analysis of Errors in Four GPM-Based Precipitation Estimations over Mainland China. Remote Sens. 2018, 10, 1420. [Google Scholar] [CrossRef]
- Tang, G. Characterization of the Systematic and Random Errors in Satellite Precipitation Using the Multiplicative Error Model. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5407–5416. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Y.; Yang, D.; Farhan, S.B. Precipitation bias variability versus various gauges under different climatic conditions over the Third Pole Environment (TPE) region. Int. J. Climatol. 2015, 35, 1201–1211. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4. 2008. Available online: Http://srtm.csi.cgiar.org (accessed on 15 January 2022).
- Skidmore, A.K. A comparison of techniques for calculating gradient and aspect from a gridded digital elevation model. Int. J. Geogr. Inf. Syst. 1989, 3, 323–334. [Google Scholar] [CrossRef]
- Weiss, A. Topographic position and landforms analysis. In Proceedings of the Poster Presentation, ESRI User Conference, San Diego, CA, USA, 9–13 July 2001. [Google Scholar]
- Makarieva, A.M.; Gorshkov, V.G.; Li, B.-L. Precipitation on land versus distance from the ocean: Evidence for a forest pump of atmospheric moisture. Ecol. Complex. 2009, 6, 302–307. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Eylander, J.B.; Joyce, R.J.; Huffman, G.J.; Adler, R.F.; Hsu, K.l.; Turk, F.J.; Garcia, M.; Zeng, J. Component analysis of errors in satellite-based precipitation estimates. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Tian, Y.; Huffman, G.J.; Adler, R.F.; Tang, L.; Sapiano, M.; Maggioni, V.; Wu, H. Modeling errors in daily precipitation measurements: Additive or multiplicative? Geophys. Res. Lett. 2013, 40, 2060–2065. [Google Scholar] [CrossRef] [Green Version]
- Tang, S.; Li, R.; He, J. Modeling and Evaluating Systematic and Random Errors in Multiscale GPM IMERG Summer Precipitation Estimates Over the Sichuan Basin. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4709–4719. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Aghakouchak, A.; Mehran, A.; Norouzi, H.; Behrangi, A. Systematic and random error components in satellite precipitation data sets. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Haiden, T.; Pistotnik, G. Intensity-dependent parameterization of elevation effects in precipitation analysis. Adv. Geosci. 2009, 20, 33–38. [Google Scholar] [CrossRef]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Assessment of GPM-IMERG and Other Precipitation Products against Gauge Data under Different Topographic and Climatic Conditions in Iran: Preliminary Results. Remote Sens. 2016, 8, 135. [Google Scholar] [CrossRef]
- Dipu, S.; Prabha, T.V.; Pandithurai, G.; Dudhia, J.; Pfister, G.; Rajesh, K.; Goswami, B.N. Impact of elevated aerosol layer on the cloud macrophysical properties prior to monsoon onset. Atmos. Environ. 2013, 70, 454–467. [Google Scholar] [CrossRef]
- Basist, A.; Bell, G.D.; Meentemeyer, V. Statistical relationships between topography and precipitation patterns. J. Clim. 1994, 7, 1305–1315. [Google Scholar] [CrossRef]













| Statistical Metric | Equation | Perfect Value | |
|---|---|---|---|
| Continuous statistical metrics | CC | 1 | |
| RB | 0 | ||
| Contingency statistical metrics | POD | 1 | |
| FAR | 0 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Tang, S.; Shi, Z.; He, J.; Shi, W.; Li, X. Spatial Patterns of Errors in GPM IMERG Summer Precipitation Estimates and Their Connections to Geographical Features in Complex Topographical Area. Remote Sens. 2022, 14, 4789. https://doi.org/10.3390/rs14194789
Li R, Tang S, Shi Z, He J, Shi W, Li X. Spatial Patterns of Errors in GPM IMERG Summer Precipitation Estimates and Their Connections to Geographical Features in Complex Topographical Area. Remote Sensing. 2022; 14(19):4789. https://doi.org/10.3390/rs14194789
Chicago/Turabian StyleLi, Rui, Shunxian Tang, Zhao Shi, Jianxin He, Wenjing Shi, and Xuehua Li. 2022. "Spatial Patterns of Errors in GPM IMERG Summer Precipitation Estimates and Their Connections to Geographical Features in Complex Topographical Area" Remote Sensing 14, no. 19: 4789. https://doi.org/10.3390/rs14194789
APA StyleLi, R., Tang, S., Shi, Z., He, J., Shi, W., & Li, X. (2022). Spatial Patterns of Errors in GPM IMERG Summer Precipitation Estimates and Their Connections to Geographical Features in Complex Topographical Area. Remote Sensing, 14(19), 4789. https://doi.org/10.3390/rs14194789