A Review of Marine Gravity Field Recovery from Satellite Altimetry

Abstract

Marine gravity field recovery relies heavily on satellite altimetry. Thanks to the evolution of altimetry missions and the improvements in altimeter data processing methods, the marine gravity field model has been prominently enhanced in accuracy and resolution. However, high-accuracy and high-resolution gravity field recovery from satellite altimeter data remains particularly challenging. We provide an overview of advances in satellite altimetry for marine gravity field recovery, focusing on the impact factors and available models of altimetric gravity field construction. Firstly, the evolution of altimetry missions and the contribution to gravity field recovery are reviewed, from the existing altimetry missions to the future altimetry missions. Secondly, because the methods of altimeter data processing are of great significance when obtaining high-quality sea surface height observations, these improved methods are summarized and analyzed, especially for coastal altimetry. In addition, the problems to be resolved in altimeter data processing are highlighted. Thirdly, the characteristics of gravity recovery methods are analyzed, including the inverse Stokes formula, the inverse Vening Meinesz formula, Laplace’s equation, and least squares collocation. Furthermore, the latest global marine gravity field models are introduced, including the use of altimeter data and processing methods. The performance of the available global gravity field model is also evaluated by shipboard gravity measurements. The root mean square of difference between the available global marine gravity model and shipboard gravity from the National Centers for Environmental Information is approximately 5.10 mGal in the low-middle latitude regions, which is better than the result in high-latitude regions. In coastal areas, the accuracy of models still needs to be further improved, particularly within 40 km from the coastline. Meanwhile, the SDUST2021GRA model derived from the Shandong University of Science and Technology team also exhibited an exciting performance. Finally, the future challenges for marine gravity field recovery from satellite altimetry are discussed.

1. Introduction

Marine gravity is a crucial component of the marine environment, and precise marine gravity information is essential to investigate the marine geological structure, explore marine resources, construct the Earth’s gravity field, etc. [1,2,3,4]. High-accuracy gravity information can be obtained from shipboard and airborne measurements [5], but it is limited by sparse coverage over the global ocean [6] and is inaccessible in certain regions owing to political reasons [7]. Satellite altimetry is nowadays the most important tool for recovering the marine gravity field since the altimetric gravity it provides has a uniform global distribution and consistent precision [8,9,10,11,12,13,14,15].

The advancement of satellite altimetry has substantially strengthened our understanding of the marine gravity field [11,16]. The evolution of altimetry missions has provided multi-source altimeter data for marine gravity field recovery, and advances in altimeter observations (altimeter range precision and spatial coverage) have considerably contributed to the marine gravity model recovery in accuracy and resolution [17,18]. Furthermore, improvements in altimeter data processing methods have also been made to refine the gravity model [15,19]. Accordingly, it is necessary to present recent advances in satellite altimetry for marine gravity field recovery.

Marine gravity field model accuracy is also influenced by gravity field recovery methods. Although these methods are now quite stable, there are advantages and disadvantages to different methods [20,21]. Thanks to multi-satellite altimeter data and improvements in altimeter data processing methods as well as gravity field recovery methods, marine gravity field models have been consistently constructed and released [9,13,22,23]. Consequently, we present a review on the characteristics of gravity field recovery methods, the progress of marine gravity field modeling, and the performance of the latest models.

The review is organized as follows: Section 2 reviews the evolution of altimetry missions from altimeter operating modes and their contribution to marine gravity field recovery. Section 3 summarizes the recent advances in altimeter data processing methods, especially in coastal and complicated sea surface regions. Section 4 reviews the advantages and disadvantages of different marine gravity field recovery methods. Section 5 reviews global marine gravity field modeling and the performance of available models. Section 6 presents the conclusions and recommendations for future research.

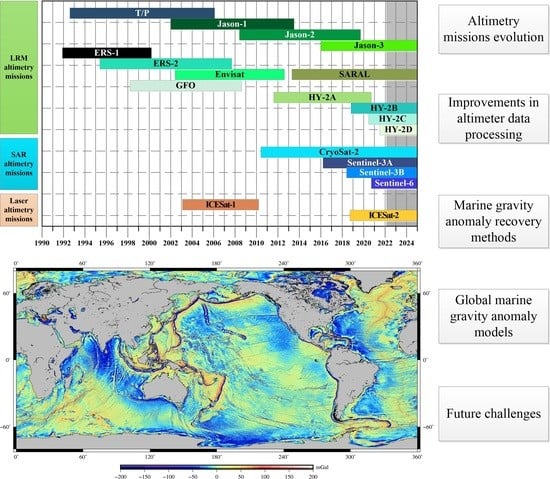
2. Altimetry Missions of Different Modes

The past 50 years have witnessed the successful implementation of more than 20 altimetry satellites. The information on the main altimetry missions is provided in Appendix A. Satellite altimetry involving sea surface observation has developed various altimeter operating modes [24], including low-resolution mode altimetry (LRM altimetry), synthetic aperture radar mode altimetry (SAR mode altimetry), and laser altimetry. In order to further enhance the range of observation accuracy and spatial coverage of the altimeter data, new altimetry operating modes have also been proposed, such as wide-swath interferometric mode altimetry, twin-satellite tandem altimetry, and GNSS-R (reflectometry) altimetry.

2.1. LRM Altimetry Missions

Sea surface height (SSH) observations with satellite altimetry refer to the average value within a certain area. The range of this certain area is usually represented by the diameter of the pulse footprint. In the conventional pulse-limited mode, the diameter of the pulse footprint under general ocean conditions (significant wave height, SWH: 2 m) generally reaches up to several kilometers; hence, the conventional pulse-limited radar altimetry is usually known as LRM altimetry [25].

From 1973 to 1985, the United States pioneered the development of a series of early satellite altimetry missions (Skylab, GEOS-3, Seasat, and Geosat), providing initial altimeter data for marine gravity field recovery. In 1985, the Soviet Union also implemented the satellite altimetry mission GEO-IK, used for Earth’s refined gravity field construction [26]. In the 1990s, the European Space Agency successively implemented the ERS-1 and ERS-2 altimetry missions. Along with Geosat data, the altimeter data from the ERS-1 and ERS-2 dramatically improved the accuracy and spatial resolution of the marine gravity field model, particularly the ERS-1 Geodetic Mission (GM) data [27,28,29].

The above altimetry missions mainly employed a single-frequency altimeter. To improve the altimetry range observation, the TOPEX/Poseidon (T/P, 1992–2005) satellite, operated jointly by the United States and France, employed a dual-frequency altimeter. Subsequently, altimetry missions such as the Jason series (Jason-1, Jason-2, and Jason-3) satellites, Envisat, and the Haiyang-2 series (HY-2A, HY-2B, HY-2C, HY-2D) of China were all equipped with a dual-frequency altimeter. The accuracy of satellite altimetry range observation was increased to the centimeter level by combining the dual-frequency altimeter with precision orbit determination [30].

Moreover, the Jason-1, Jason-2, and HY-2A performed GM and provided intensive altimeter data. These GM data, along with ERS-1/GM and Geosat/GM data, further strengthened the spatial coverage of the along-track altimeter data and enhanced the resolution and accuracy of the marine gravity field model [21,31,32]. The LRM altimetry missions have ushered in a new chapter of prosperous development.

The SARAL altimetry mission, jointly operated by India and France, employed a Ka-band (35 GHz) altimeter. The Ka-band altimeter has a higher frequency than the conventional altimeter (Ku/C band), with observations less affected by the ionosphere delay. Furthermore, the diameter of the pulse footprint of the Ka-band altimeter is reduced to ~1.4 km under general ocean conditions, and the ranging accuracy is improved to 1–2 cm [33]. With the improvement of ranging accuracy, SARAL altimeter data play an important role in high-accuracy marine gravity field recovery [22,34]. The altimetry mission GEO-IK-2, implemented by Russia in 2016, also employed a Ka-band altimeter [35]. The Ka-band altimeter is a step forward to the future of altimetry, although with possible drawbacks.

2.2. SAR Mode Altimetry Missions

Unlike traditional LRM altimetry, which uses only the frequency and amplitude of the electromagnetic wave, SAR altimetry also uses phase information [36]. With Doppler shifts technology, the pulse footprint of the SAR altimeter is reduced to a few hundred meters in diameter, enabling altimeter data closer to the coastline [37].

The CryoSat-2 mission, implemented by ESA, operates in SAR mode over a few parts of the Earth. Compared with the LRM mode altimeter data, Cryosat-2 SAR mode along-track altimeter data have an along-track resolution of 300 m [38,39]. Sentinel-3A and Sentinel-3B, inherited from Cryosat-2, operate entirely in SAR mode on a global scale. Subsequently, Jason-CS (including Sentinel-6A, and Sentinel-6B), belonging to the T/P-Jason series, also operate in SAR mode [40]. Combined with altimeter data from the SAR mode, the accuracy of the local marine gravity anomaly model is further enhanced, especially in areas close to offshore islands [12]. The high-resolution data provided by SAR mode altimeters will continuously improve the precision of global marine gravity field recovery.

The CryoSat-2 satellite has performed geodetic missions throughout its life cycle. With the accumulation of multi-satellite altimeter data, the ground track spacing of GM data at the equator is better than 7 km from Cryosat-2, SARAL, Jason-1, Jason-2, HY-2A, etc. These GM altimeter data greatly contribute to high-accuracy gravity field recovery in which Cryosat-2 altimeter data play an important role [8,17].

2.3. Laser Altimetry Missions

The pulse footprint diameter of the laser altimeter has been lowered to meter-level compared to the diameters of the LRM and SAR mode radar altimeters. Currently, the main laser altimetry missions are the ICESat and ICESat-2 satellites. The ICESat satellite, operated by the United States, provides novel along-track data for marine gravity field recovery, especially in Antarctic coverage [9]. The ICESat-2 satellite, the 2nd-generation laser altimeter ICESat mission, employs an advanced topographic laser altimeter system (ATLAS) with three pairs of laser beams (six beams), which can obtain altimeter data at a ground spacing of about 3.3 km between adjacent beams pairs [41]. The ICESat-2 altimeter data satellite has also been used to recover the marine gravity field in certain regions, and it is anticipated that this data will be crucial for improving the resolution of the model [42].

2.4. Advanced Modes Altimetry Missions

Expanding the application for understanding the mesoscale and microscale marine phenomena from satellite altimetry involves the use of high-resolution and high-accuracy altimeter data. If the goals are to be achieved, more satellites and a longer observation period are required to obtain the data under the existing altimeter operating mode. As a result, it is urgently necessary to develop new altimeter operating modes for altimetry missions.

Wide-swath interferometric altimetry is now being developed as a priority for next-generation altimetry missions. The SWOT (Surface Water and Ocean Topography) satellite, jointly developed by NASA (America), Centre National d’Etudes Spatiales (CNES, French), and the Canadian Space Agency, is designed to be equipped with a new Ka-band radar interferometric altimeter (KaRIN) and to obtain two-dimensional altimeter data with a width of up to 120 km [43]. Theoretically, altimeter data with a grid resolution of 2 km × 2 km can be obtained by the SWOT satellite. Based on simulated wide-swath SSHs, the SWOT observation has the potential advantage of delivering a high-quality marine gravity field model [12,44].

In addition to the SWOT mission, other missions with wide-swath interferometric altimetry have been designed by different institutions. The Japan Aerospace Exploration Agency (JAXA) proposed a new generation of the X-band wide-swath interferometric altimetry mission COMPIRA [45]. The China Academy of Space Technology has also conducted tests of the wide-swath interferometric altimeter using Tiangong-2. The tests confirmed the advantage of wide-swath altimeter data in spatial resolution [46]. In 2016, the Pilot National Laboratory for Marine Science and Technology (Qingdao) put forward the concept design of the “Guanlan” science mission, which is expected to use the dual-frequency (Ka and Ku) interferometric altimeter [47].

To achieve accuracy of 1 mGal and resolution of 1′ × 1′ for the altimetric gravity field, a new twin-satellite altimetry was proposed [48]. In this mode, two satellites are able to obtain altimeter data with a ground track spacing of 1 arcmin, combined with the Earth’s rotation. The altimeter data obtained by twin-satellite can be used to eliminate common errors and improve the spatial coverage of SSH observations in the east–west direction. It is anticipated that the marine gravity field recovery will be of excellent quality.

The study of new mode altimetry has also focused heavily on GNSS-R altimetry. Because of its numerous signal sources, GNSS-R is anticipated to enhance the spatial resolution of altimeter data as compared to radar altimetry or laser altimetry. GNSS-R altimetry techniques mainly include delay altimetry, phase altimetry, and interferometric mode technology [49], and these three techniques have their own advantages and disadvantages. Research institutions have conducted verification of various GNSS-R altimetry techniques based on space-borne, airborne, and shore-based data [50,51,52]. In the future, more research and specialized low-orbit satellite constellations for altimetry will be needed to confirm the adaptability of GNSS-R altimetry.

3. Altimeter Data Processing

The processing of altimeter data varies slightly depending on the application of satellite altimetry. For marine gravity field recovery, altimeter data processing mainly includes range corrections, altimeter data processing for different missions, and multi-satellite altimeter data fusion.

3.1. Range Corrections

SSH observation accuracy depends mainly on the accuracy of the satellite orbit determination and the altimeter range corrections. Because of the development of precise orbit determination technology, including GPS, DORIS, and SLR, the accuracy of radial orbit error has reached the centimeter level of SSH observation [19]. The range corrections generally include altimeter instrument error corrections, atmospheric propagation delay corrections, geophysical corrections, and waveform retracking correction.

Instrument error is mainly caused by the altimeter hardware, usually using the calibration sites for instrument error corrections. At present, several mature offshore calibration and validation (Cal/Val) sites for satellite altimetry have been developed around the world [53], such as the Harvest platform site (America), the Corsica site (French), the Crete/Gavdos site (Greece/ESA), and the Bass Strait site (Australia). China is also developing the Wanshan Cal/Val site specifically for the HY-2 series missions [54]. These Cal/Val sites play an important role in the altimeter instrument error corrections and absolute calibration of SSH observation. Because of the novel along-track data obtained from new altimetry missions as well as the development of altimeter operating mode, new challenges are being posed to the calibration of altimeter data [55].

The atmospheric delay corrections, geophysical corrections, and waveform retracking corrections are quite stable for open ocean altimeter data range corrections [19]. In coastal and complicated sea surface regions, however, these range corrections are currently considered the main factor contributing to the uncertainty of the SSH observation accuracy [56,57]. Accordingly, the follow-up parts have mainly focused on the corrections methods in the coastal and complicated sea surface areas.

The atmospheric delay corrections include the ionospheric delay correction and the tropospheric delay corrections. The ionospheric correction is generally derived from dual-frequency (Ku, C/S band) altimeter range measurements for altimetry missions after the 1990s [58]. Unfortunately, the two range measurements of dual-frequency have inconsistent accuracy owing to ionospheric delay dependent on frequency, such that a noisier correction would result from the dual-frequency range measurements [59]. To reduce the error of dual-frequency correction, an along-track low-pass filter is typically used to smooth the dual-frequency ionospheric correction [60]. In order to further mitigate the effects of ionospheric delay, the high-frequency (Ka-band) altimeter was developed for altimetry missions [34]. In coastal areas or inland water, the ionospheric correction is also derived from global ionospheric models when the dual-frequency range measurements are contaminated by land or invalid. The global models include the International References Ionosphere (IRI) [61], NIC09 [62], and Global Ionospheric Maps (GIM) [63]. The IRI represents the early attempts to model the ionosphere, but it is now rarely employed to correct altimeter range measurements owing to the low temporal resolution. The total electron content (TEC) used in the GIM and NIC09 is usually derived from GNSS observations, so additional altitude scaling is necessary for TEC data to estimate the ionospheric correction [64]. The commonly used scaling factors are 0.925 for satellites around an altitude of 1350 km, 0.856 for those around 800 km, and 0.844 for those around 730 km. Although the ionospheric model correction accuracy was improved by accurate estimates of TEC, the ionospheric models are inadequate for high-accuracy altimetry, especially in coastal areas and complicated sea surface areas [65,66,67]. Consequently, highly precise and long-term stable ionospheric corrections are still necessary for coastal altimeter range correction.

The tropospheric delay corrections include the dry tropospheric correction and the wet tropospheric correction (WTC). The WTC is considered to be a large sources of error and uncertainty in SSH observation because of the relatively low accuracy of water vapor estimation [68]. The WTC is generally obtained from the water vapor content from the on-board microwave radiometer (MWR) [69], with a high-accuracy in the open ocean. However, the accuracy of the WTC may be highly degraded by the contamination from land, rain, and ice, particularly in coastal or complicated sea surface areas. To ameliorate the WTC derived from the MWR, various correction methods have been developed over the open ocean and coastal areas. An overview of the various methods is available in [57,70]. Among those methods, the mixed-pixel algorithm (MPA) [71] and GPD+ algorithms [72] were revealed as the optimal methods to derive valid and continuous WTC by minimizing land and ice effects or combining all existing wet path delay measurements [73]. The WTC that is not obtained from the MWR is obtained from models produced by the European Centre for Medium-Range Weather Forecasts (ECMWF). In general, the WTC derived from models is not superior to the well-calibrated MWR. Although the WTC has been improved by various methods, a new generation of MWR and specialized retrieval methods equipped to capitalize on fresh information are necessary for the WTC not only in coastal areas and in the open ocean [74]. Meanwhile, the high-resolution WTC is also expected for SAR mode altimetry and future wide-swath interferometric altimetry [75].

Geophysical corrections generally include tidal corrections, dynamic atmospheric corrections, and sea state bias (SSB) correction. The tidal corrections are mostly obtained from global ocean tide models, including GOT4.10, EOT20, and FES2014. The GOT4.10 and EOT20 releases are both based on empirical tidal analysis of multi-satellite altimeter data. The GOT4.10 model is a collection of both global and regional models blended at mutual boundaries with a regular grid of 0.5° [76]. The EOT20 model makes full use of residual signals estimated by the reference tidal model FES2014 and improved coastal SSH observation from ALES retracker, with a regular grid of 1/8° [77]. The FES2014 release is based on a hydrodynamic solution and an assimilation process, with a regular grid of 1/16° [78]. The GOT4.10 and FES2014 models are operationally used in current altimeter geophysical data records (GDRs) [79]. Benefiting from data both motivated by and the result of satellite altimetry, the accuracy of global tide modes has advanced considerably, especially in coastal areas and in the deep ocean [80,81]. Based on the last accuracy assessment of global tide modes, there is approximately 0.9 cm of root sum square differences between the model and tide observations (bottom pressure data or tide gauges) in the deep ocean [82]. However, the differences comprise nearly several centimeters in the coastal areas, and there is a significant gap across models in high latitudes [83]. All the modes are still imperfect on basin and sub-basin scales, particularly close to Antarctica [84].

The dynamic atmospheric correction (DAC) is generally derived from a barotropic model forced by atmospheric pressure and wind [85]. The DAC has been improved by more than 3 cm in the open ocean and in some coastal areas, benefiting from the ERA-Interim meteorological reanalysis produced by the European Centre for Medium-Range Weather Forecasts (ECMWF) [86]. The DAC derived from the ERA-Interim meteorological reanalysis is a combination of the high and the low frequencies of the inverted barometer, and it is used in altimeter GDRs. Still, the fundamental issue with the DAC is that the accuracy of the model varies regionally, decreasing the closer it is to the coastline [87].

The SSB correction is also considered as a large source of uncertainty in SSH observation. There are two kinds of estimation for SSB correction: the parametric estimation [88] and the non-parametric estimation [89] based on empirical models. The parametric estimation is performed with different unknown parameters regarding significant wave height and wind speed. Based on the SSB modeling of different unknown parameters, functions with three, four, and six unknown parameters are commonly used for SSB models [90]. In coastal areas, considering that the parametric estimation has superior extensibility, regional SSB models are also built based on various waveform retracking methods [91,92]. The solution of unknown parameters for the parametric estimation is based on SSH discrepancies at the crossover or at repeat ground tracks, which is only an approximation of the SSB differences [93]. In this case, the non-parametric estimation is widely used in altimeter data GDRs because it does not presuppose specific functional relationships between SSB and SWH, wind speed [90]. The regression estimation, kernel function, and window width have a significant impact on the SSB correction derived from the non-parametric estimation. More recently, studies have shown that the determination of appropriate regression estimations, kernel functions, and global/local window width can improve the accuracy of the SSB correction [94,95,96]. On the basis of the SSB model as a function of SWH and wind speed, the mean wave period is also introduced as the third variable in the non-parametric estimation, which can further improve the SSB correction [97,98,99]. Unfortunately, theoretical modeling and understanding of the SSB remain difficult, so the accuracy of SSB correction is still uncertain.

Waveform retracking is a prominent issue for altimeter range corrections because of the variety of echo waveforms induced by non-homogeneous sea surfaces and the adaptability of different methods. In the open ocean, waveform retracking methods are quite stable for the standard waveforms reflected from sea or sea-ice surfaces [100]. In coastal or complicated sea surface areas, to solve the problem of retracking failure for the integral waveform, sub-waveform waveform retracking has been proposed to obtain range correction from the partial waveform, including the sub-waveform threshold method [101], the ALES method [102], and the spatiotemporal altimetry retracking (STAR) method [103]. On the basis of sub-waveform retrackers, a new retracker was proposed to detect peak-type noise and compensate for the power deficit of waveform trailing edges [104]. To optimize the estimated parameters of waveform retracking, smooth estimation retracking was developed [105]. Considering the interference of echo noise in waveform retracking, a family of waveform retracking methods based on waveform denoising (singular spectrum analysis retacking, singular value decomposition retracking, waveform decontamination retracking, etc.) was presented [106,107,108], which effectively improves the accuracy of retracked SSHs. To improve the SSH gradient accuracy, a two-pass waveform retracking was proposed [32,109]. The retracked SSHs from the two-pass retracking method contribute to high-accuracy marine gravity field recovery when compared with the result from conventional retracking methods. The above methods, undoubtedly, have been great achievements in waveform retracking [110,111]. However, an integrated method is needed to handle altimeter waveforms with different characteristics, with the development of retracking methods. It must be improved for open ocean and coastal areas.

3.2. GM and ERM Data Processing

After range error corrections, there remain residual systematic errors and high-frequency errors in the altimeter data. Generally, altimeter data are processed with different methods according to the GM and ERM altimeter data characteristics.

For GM data, Gaussian filtering is commonly used to reduce the high-frequency noise in the along-track altimeter data. For filtering methods, both methods are crucial to error correction [60] and the marine gravity field model [22]. The key to the filtering is to determine the appropriate filter radius, which will have an impact on the marine gravity field recovery [21].

For ERM data, the collinear adjustment is commonly used to weaken the residual systematic errors and high-frequency errors [112]. When recovering the marine gravity field, it is not necessary for the crossover adjustment. The main reason is that the along-track SSH gradients are used as input data for marine gravity field recovery, which can attenuate residual system errors [10].

After GM and ERM data processing, the residual errors of SSH observation can be further mitigated by marine gravity field recovery methods based on vertical deflection [22,23]. A detailed description combining the introduction of marine gravity recovery methods is provided in Section 5.

Although the GM and ERM data are processed using a variety of methods, it is still a challenge to utilize altimeter data with different characteristics. For instance, the accuracy of the ERM altimeter data after collinear adjustment is significantly higher than that of GM data [113]. Furthermore, the GM data have a higher spatial resolution compared to ERM data.

3.3. Multi-Satellite Altimeter Data Fusion

Multi-satellite altimeter data fusion is necessary for marine gravity field recovery, and the key is to determine the weight of each satellite’s altimeter data. The SSH crossover discrepancy is a common method to determine the weight of each satellite’s altimeter data [114]. For altimeter data from the Ka-band, however, the crossover discrepancy method is not effective in determining the weight of altimeter data. To improve the marine gravity field recovery accuracy from Ka-band and Ku-band altimeter data, an iterative method was proposed and used to determine the weight of Ka-band altimeter data, and the crossover discrepancy method was used to determine the weights of Ku-band altimeter data [113]. In addition, for different time periods of altimeter data from a single satellite, the method based on the root mean square of high-frequency altimeter data and the utilization rate of waveform was proposed to further improve the accuracy of marine gravity field recovery [115].

Along with the development of altimetry missions, altimeter data are obtained from different band (Ku-band and Ka-band) altimeters and altimeter operating modes. How to evaluate the quality of altimeter data for specific application purposes and determine the weights of altimeter data are still key in multi-satellite altimeter data fusion.

4. Marine Gravity Field Recovery Methods

Marine gravity field recovery methods, including the inverse Stokes formula, Laplace’s equation, inverse Vening Meinesz formula, and least squares collocation, are now quite stable with the advancement of satellite altimetry technology.

4.1. Inverse Stokes Formula

The inverse Stokes formula is used to recover marine gravity anomalies by using the geoid undulations as input data [116]. The formula is as follows:

$$\Delta g=-\frac{\overline{\gamma }}{R}{N}_p-\frac{\overline{\gamma }}{16\mathsf{\pi }R}{\displaystyle \underset{\sigma }{\iint }\frac{N_q-N_p}{{\sin }^3\frac{{\psi }_{pq}}{2}}}d\sigma ,$$

(1)

where $\Delta g$ is the marine gravity anomaly, $R$ is the average radius of Earth, $\overline{\gamma }$ is normal gravity, ${\psi }_{pq}$ is the spherical distance between two points, $N_p$ and $N_q$ are the geoid heights, $p$ stands for the calculation point, and $q$ for the flow point.

The geoid undulations are generally obtained from along-track SSH by subtracting mean dynamic topography (MDT). The MDT model commonly used includes DTU series models [117] and CNES-CLS series models [118]. The MDT solutions are calculated by merging the mean sea level from altimeter data and the geoid model from satellite gravity data [119]. Although the MDT has benefited from a number of improvements, the model’s resolution currently depends on satellite gravity data at 100 km resolution [120]. Consequently, the dynamic topography model with high resolution is one of the issues with this approach (and maybe not the biggest), and it is also an issue with other methods. All methods depend on the sea surface matching the geoid, and the extent to which there are unknown differences between the two is an issue.

The innermost zone effect is a key problem in the calculation of gravity anomalies by the inverse Stokes formula because of the singular integrals between adjacent points. This problem also exists for the inverse Vening Meinesz formula, so they will be explained together in the following method introduction.

4.2. Inverse Vening Meinesz Formula

The inverse Vening Meinesz formula is used to recover marine gravity anomalies by using the vertical deviations as input data. The commonly used equation is as follows:

$$\Delta g=\frac{\overline{\gamma }}{4\mathsf{\pi }}{\displaystyle \underset{\sigma }{\iint }{H}^{\prime }\left({\xi }_q\cos {\alpha }_{qp}+{\eta }_q\sin {\alpha }_{qp}\right)}d{\sigma }_q,$$

(2)

where $\Delta g$ is the gravity anomaly, $\overline{\gamma }$ is the normal gravity, and ${\xi }_q$ and ${\eta }_q$ are the meridian and prime components of vertical deflection, respectively. ${\alpha }_{qp}$ is the azimuth from the q point to the p point. $d{\sigma }_q$ is the areal element of the unit sphere $\sigma$.

The kernel function $H^{\prime }({\psi }_{pq})$ is described in [28] as

$$H^{\prime }({\psi }_{pq})=\frac{\cos (\raisebox{1ex}{${\psi }_{pq}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)}{2\sin (\raisebox{1ex}{${\psi }_{pq}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)}\left(-\frac{1}{\sin (\raisebox{1ex}{${\psi }_{pq}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)}+\frac{3+2\sin (\raisebox{1ex}{${\psi }_{pq}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)}{1+\sin (\raisebox{1ex}{${\psi }_{pq}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)}\right),$$

(3)

where ${\psi }_{pq}$ is the spherical distance between p point and q point.

Equation (2) can be rigorously evaluated by the 1-D fast Fourier transform (FFT) method to solve for the integral,

$$\Delta g_{{\phi }_p}=\frac{\overline{\gamma }\Delta \phi \Delta \lambda }{4\mathsf{\pi }}{F}^{-1}\left\{{\displaystyle \sum _{{\phi }_p}\cos {\phi }_p\left\{F_1\left[H^{\prime }(\Delta {\lambda }_{qp})\cos {\alpha }_{qp}\right]\cdot F_1({\xi }_q)+F_1\left[H^{\prime }(\Delta {\lambda }_{qp})\sin {\alpha }_{qp}\right]\cdot F_1({\eta }_q)\right\}}\right\},$$

(4)

where $\Delta \phi$ and $\Delta \lambda$ are the grid interval in latitude and longitude, respectively. $F_1$ is the 1-D FFT.

The innermost zone effect is also a key problem in the calculation of gravity anomalies by the inverse Vening Meinesz formula, similar to the inverse Stokes formula. To recover gravity anomalies in the innermost zone, the calculation equation is derived by assuming the shape of the innermost zone (circle and square) [28,121]. In addition, to improve the calculation accuracy and efficiency, the shape of the innermost zone is approximately rectangular, and the non-singular transformation is adopted to calculate gravity anomalies [122].

4.3. Laplace’s Equation

The relationship between gravity disturbance (over the ocean) and vertical deflection can be established based on Laplace’s equation [6],

$$\frac{\partial \delta g}{\delta z}=-{\gamma }_0\left(\frac{\partial \xi }{\partial x}+\frac{\partial \eta }{\partial y}\right).$$

(5)

The gravity anomalies solution in the wavenumber domain can be deduced by Fourier transformation,

$$\delta g(k,0)=\frac{i}{\left|k\right|}\overline{\gamma }\left[F^{-1}\left[k_x\xi (k)\right]+F^{-1}\left[k_y\eta (k)\right]\right],$$

(6)

where $\left|k\right|=\sqrt{k_x^2+k_y^2}$, $k_x$ and $k_y$ are spatial frequencies, $\xi (k)$ and $\eta (k)$ are the Fourier transform of the meridian and prime components of vertical deflection, respectively. $\delta g$ is gravity disturbance [20].

Once these methods are expressed as Fourier transforms, including the inverse Stokes formula, inverse Vening Meinesz formula, and Laplace’s equation, all depend on (or are related to) Laplace’s equation.

The gravity anomalies can be calculated from $\delta g$ by

$$\Delta g(x,y)=\delta g(x,y)-\frac{2}{R}T(x,y)=\delta g(x,y)-2\frac{{\gamma }_0}{R}N(x,y).$$

(7)

Vertical deflection is used as the input data in the marine gravity field recovery by the inverse Vening Meinesz formula and Laplace’s equation. Vertical deflection is generally obtained from the along-track SSH gradient, which can effectively attenuate the residual errors in the altimeter data compared to using SSHs directly to recover the gravity anomalies. Meanwhile, the solution of vertical deflection depends on the wavelength of SSH observation. To solve vertical deflections, several methods have been proposed. The method proposed by Sandwell and Smith [6] is used to solve the grid of vertical deflection using the derivative of the geoid height and the satellite’s velocity on the ground track crossover. Crossover adjustment is not commonly applied with this method, but that is a reasonable approach provided the discrepancies can be ignored for the wavelengths of interest. At a smaller scale and for higher accuracy, this can still be an issue. In addition, this method cannot accurately solve for the vertical deflection in the regions without SSH crossover [123]. The method proposed by Hwang et al. [28] is based on the geoid height gradients on the crossover from arbitrary ground tracks and adjacent to the crossover. This method makes full use of the along-track geoid height gradient information but is also limited by the absence of SSH crossover. The least squares collocation (LSC) is a method of directly calculating the vertical deflection, and it is unnecessary for the geoid height gradient on the crossover [124]. Since the LSC is also a marine gravity recovery method, the characteristics of the LSC are presented in Section 4.4.

For using vertical deviations to recover gravity anomalies, a key issue is determining the weights of the meridian and prime component of vertical deflection [125]. The main reason is that the accuracy of recovering marine gravity anomalies is impacted by an imbalance in the accuracy of the meridian and prime components [126,127]. To determine the weights, a method is proposed based on the covariance between the meridian and prime components, as well as their error variances in relation to the reference gravity field [124,125,128], which provides a new idea for improving the accuracy of gravity anomalies.

4.4. Least Square Collocation

The least squares collocation is also often used to recover gravity anomalies according to the relationship between geoid gradients and the gravity anomalies [124]. The commonly used equation is

$$\Delta g=C_{\Delta ge}{(C_{ee}+C_{nn})}^{-1}{e}_{res}+\Delta g_{ref},$$

(8)

$$M_g^{}=C_{\Delta g\Delta g}-C_{\Delta ge}{(C_{ee}+C_{nn})}^{-1}{C}_{e\Delta g},$$

(9)

where $C_{\Delta ge}$ is the covariance between residual gravity anomalies and residual geoid gradients, $C_{ee}$ is the covariance between residual geoid gradients and residual geoid gradients, $C_{nn}$ is the noise variance of geoid gradients, $e_{res}$ is the residual geoid gradients, $\Delta g_{ref}$ is the gravity anomaly from the reference field, $C_{\Delta g\Delta g}$ is the covariance between residual gravity anomalies, and $M_g^{}$ is the standard deviation of gravity anomalies recovery.

The LSC is used to recover gravity anomalies by integrating multiple-source gravity data, including altimeter data, shipboard and airborne gravity measurements [129]. Gravity anomalies obtained by LSC are smoother than the results of other methods even if somewhat time-consuming; the LSC is frequently used in complex sea surface regions [130,131]. The most important use of LSC is to determine the noise covariance matrix, particularly in various regions. However, the key parameters (covariance and variance) in the LSC are generally obtained from global anomalous gravity potentials [113]; accurately determining the key parameters within different regions remains challenging.

As mentioned above,

Table 1. Several methods impacted by different issues.

Methods	Issues
Inverse Stokes formula	MDT + innermost zone effect
Inverse Vening Meinesz formula	MDT + innermost zone effect + imbalance accuracy of vertical deflection components
Laplace’s equation	MDT + imbalance accuracy of vertical deflection components
Least squares collocation	MDT + Key parameters (covariance matrix) determination

summarizes several methods impacted by different issues.

5. Global Marine Gravity Anomaly Model

5.1. Global Gravity Anomaly Model

The accumulation of altimeter data and improvements in data processing have substantially increased the accuracy and resolution of the marine gravity anomaly model in both the global and regional models [9,22,132]. The advancement of the global gravity model is here presented since it is not practical to analyze the progress of the regional gravity model. The developed and released global gravity models primarily include the Sandwell and Smith (S&S) series model developed by the Scripps Institution of Oceanography (SIO) team and the KMS-DNSC-DTU series model developed by the Technical University of Denmark, etc.

The S&S series model recovery method employs Laplace’s equation [6]. The two-pass waveform retracking is used to improve the SSH gradients [34,109], and the depth-dependent 2-D filter is used in the final model [22]. More than two dozen versions of the S&S series model have been released since 2010, and information about each version can be found in Appendix B (

Table A2. Sandwell and Smith series global marine gravity anomaly models.

Version	Year	Reference Gravity Field	Grid Resolution	Coverage Range	Altimeter Data
V19.1	2012	EGM2008	1′ × 1′	80.7°S~80.7°N	Ge + E1 + T/P + E2 + J1 + En + C2
V20.1	2012	EGM2008	1′ × 1′	80.7°S~80.7°N	Ge + E1 + T/P + E2 + J1 + En + C2
V21.1	2013	EGM2008	1′ × 1′	80.7°S~80.7°N	Ge + E1 + T/P + E2 + J1 + En + Cr2
V22.1	2013	EGM2008	1′ × 1′	85°S~85°N	Ge + E1 + T/P + E2 + En + J1+ + C2
V23.1	2014	EGM2008	1′ × 1′	85°S~85°N	Ge + E1 + T/P + J1 + E2 + En + C2
V24.1	2016	EGM2008	1′ × 1′	85°S~85°N	Ge + E1 + T/P + J1 + E2 + En + C2
V25.1	2017	EGM2008	1′ × 1′	85°S~85°N	Ge + E1 + T/P + J1 + E2 + En + C2 + Al
V26.1	2018	EGM2008	1′ × 1′	85°S~85°N	Ge + E1 + T/P + J1 + E2 + En + C2 + Al
V27.1	2018	EGM2008	1′ × 1′	85°S~85°N	Ge + E1 + T/P + J1 + E2 + En + C2 + Al + J2
V28.1	2019	EGM2008	1′ × 1′	85°S~85°N	T/P + J1 + E2 + En + C2 + Al + J2
V29.1	2019	EGM2008	1′ × 1′	85°S~85°N	T/P + J1 + E2 + En + J2 + C2 + Al + S3A + S3B
V30.1	2020	EGM2008	1′ × 1′	85°S~85°N	T/P + J1 + E2 + En + J2 + C2 + Al + S3A + S3B
V31.1	2021	EGM2008	1′ × 1′	85°S~85°N	T/P + J1 + E2 + En + J2 + C2 + Al + S3A + S3B

(Ge: Geosat, E1: ERS-1, T/P: Topex/Poseidon, J1: Jason-1, E2: ERS-2, En: Envisat, C2: Cryosat-2, Al: Saral/Altika,. J2:Jason-2, S3A: Sentinel-3A, S3B: Sentinel-3B).

). Among these versions, the V7.2 model provides the most detailed view of global ocean floor structures based on the high-density altimeter data from Geosat and ERS-1. The V23.1 model has improved enormously in accuracy and resolution compared to the V7.2 model by increasing high-density altimeter data from Cryosat-2, Jason-1, Envisat, etc. [8]. Since the contribution of early altimeter data to model enhancements has been minimal with the accumulation of altimeter data and the improvement in range observation accuracy, the V28.1 and subsequent models no longer utilize Geosat and ERS-1 altimeter data [22]. As of 2022, the latest S&S series model is the V31.1 version. The accuracy of the V31.1 model is better than 2 mGal (1 mGal = 10⁻⁵ m/s²) in certain areas, with a grid resolution of 1 arcmin [2].

The KMS-DNSC-DTU series model recovery method employs the inverse Stokes formula. The double retracking technique (similar to two-pass retracking) is used to improve the quality of altimeter data [123]. Information on each version since 2010 is presented in Appendix B (

Table A3. KMS-DNSC-DTU series global marine gravity anomaly models.

Version	Year	Reference Gravity Field	Grid Resolution	Coverage Range	Altimeter Data
DTU10	2010	EGM2008	1′ × 1′	88°S~88°N	Ge + E1 + T/P + GFO + E2 + J1+ ICESat-1
DTU13	2013	EGM2008	1′ × 1′	88°S~88°N	Ge + E1 + T/P + GFO + E2 + J1 + C2 + ICESat-1
DTU14	2014	EGM2008	1′ × 1′	88°S~88°N	Ge + E1 + T/P + GFO + E2 + J1 + C2 + ICESat-1
DTU15	2015	EGM2008	1′ × 1′	88°S~88°N	Ge + E1 + T/P + GFO + E2 + J1 + C2 + ICESat-1
DTU17	2017	EGM2008	1′ × 1′	88°S~88°N	T/P + GFO + E2 + J1 + C2 + J2 + Al + ICESat-1

(Ge: Geosat, E1: ERS-1, T/P: Topex/Poseidon, J1: Jason-1, E2: ERS-2, En: Envisat, C2: Cryosat-2, Al: Saral/Altika. J2:Jason-2, S3A: Sentinel-3A, S3B: Sentinel-3B).

). These models are focused on improving the Arctic gravity field, so the model coverage is augmented to 88°N-88°S with the Earth gravity reference field [123]. In addition to radar altimeter data, the DTU10 model also uses laser altimeter data (ICESat-1). The DTU15 and DTU17 model accuracy has been further improved by increasing the Cryosat-2 SAR and SARin mode altimeter data, particularly in the Arctic region [9]. The latest model is the DTU21 version, but it is not available for confidentiality reasons. This series model with high-accuracy is also commonly used in global gravity field models (EGM2008 and XGM2019e) construction [1,14].

Since none of the above models used the HY-2A altimeter data, the global marine gravity anomaly model was developed based on multi-satellite altimeter data, including HY-2A, by the Wuhan University of China team and the Shandong University of Science and Technology team. The Wuhan University of China team likewise used the two-pass waveform retracking, and the global model Grav_Alti_WHU (80°N-80°S, 1′ × 1′ grid) was constructed on the basis of the South China Sea experiment [10]. To integrate the Ka-band and Ku-band altimeter data, a new iterative method was proposed by the Shandong University of Science and Technology team for determining the weight of Ka-band data [113]. Likewise, the global model SDUST2021 GRA (80°N-80°S, 1′ × 1′ grid) was also constructed based on the of South China Sea experiment [23]. The SDUST2021GRA is shown in Figure 1. The differences in global marine gravity anomalies (free air) between the models are shown in Figure 2.

5.2. Model Performance

To assess the performance of global models, the latest available models (SIO V31.1, DTU17, and SDUST2021GRA) were evaluated by shipboard gravity data from the National Centers for Environmental Information (NCEI). Since the global navigation satellite system (GNSS) improved the navigation accuracy of shipboard measurements, only the shipboard gravity data collected after 1990 were used. To eliminate the gross error, the cruise data with a large root mean square (RMS) between the shipboard gravity and reference gravity field (XGM2019e), as well as the points deviating from a certain threshold relative to the reference field were removed. Furthermore, to correct the long wavelength system errors, the data of each cruise were processed by a quadratic polynomial regression [21]. With a rejection rate of 2.9%, the remaining shipboard data were 7,432,051 points from 538 cruises.

The statistics of the difference between global gravity anomaly models and shipboard gravity in different regions are listed in

Table 2. The difference between global gravity anomaly models and shipboard gravity anomalies in different regions (Unit: mGal).

	Model	Min	Max	Mean	STD	RMS
Global [–80°S, 80°N]	DTU17	−83.48	99.25	−0.21	5.85	5.85
	SDUST2021GRA	−82.97	99.12	−0.17	5.62	5.62
	SIO V31.1	−83.51	177.35	−0.12	5.51	5.51
High-latitude [−80°S, −66°S), (66°N, 80°N]	DTU17	−83.48	99.25	−1.96	11.73	11.89
	SDUST2021GRA	−82.97	99.12	−1.34	11.60	11.68
	SIO V31.1	−81.10	76.25	−3.03	10.34	10.78
Low-middle latitude [−66°S, 66°N]	DTU17	−71.85	78.44	−0.13	5.38	5.38
	SDUST2021GRA	−68.45	64.14	−0.11	5.14	5.14
	SIO V31.1	−83.51	177.35	0.02	5.10	5.10

, according to the latitude coverage of orbital inclination for altimetry missions (all missions at [–66°S, 66°N]).

In low-middle latitude regions, the RMSs for all models are significantly better than the statistical results in high-latitude regions, which suggests that the model accuracy in high-latitude regions must be further enhanced. There are two main reasons for the poor accuracy in high-latitude regions. On the one hand, some altimetry satellites, such as the T/P-Jason series, cannot obtain altimeter data in high-latitude regions, resulting in fewer altimeter data and poor accuracy in these regions. On the other hand, sea ice in high-latitude regions affects the quality of altimeter data, thereby reducing the accuracy.

Considering the variability of shipboard gravity accuracy in different regions, the RMSs of shipboard gravity crossover discrepancies were obtained, being 4.75 mGal (global), 5.56 mGal (high-latitude), and 4.47 mGal (low-middle latitude). Then the RMS of models in different regions was determined by the error propagation law on the assumption that the shipboard gravity and gravity model are independent of each other, as follows:

$${\mathrm{RMS}}_{{}_{model}}^2={\mathrm{RMS}}_{ms}^2-{(\raisebox{1ex}{${\mathrm{RMS}}_s$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2}$}\right.)}^2,$$

(10)

where ${\mathrm{RMS}}_{{}_{model}}^{}$ is the RMS of the gravity model, ${\mathrm{RMS}}_{ms}^{}$ is the RMS of the differences between altimetric gravity and shipboard gravity, and ${\mathrm{RMS}}_s$ is the RMS of shipboard gravity crossover discrepancies.

As shown in

Table 3. The RMS of the gravity model in different regions (Unit: mGal).

Region	DTU17	SDUST2021GRA	SIO V31.1
Global	4.79	4.50	4.37
High-latitude	11.22	11.00	10.04
Low-middle latitude	4.35	4.05	4.00

, although the model assessment was not strictly precise, the model accuracy in the low-middle latitude was significantly better than the accuracy in the high-middle latitude region, which was consistent with the above model. Overall, the SIO V31.1 model had an excellent performance on a global scale, which may be related to the addition of the Sentinel-3A/3B SAR altimeter data not used in the DTU17 and SDUST2021GRA models. Meanwhile, the SDUST2021GRA model also achieved an exciting performance, thanks to the addition of HY-2A data and the improvement of multi-satellite altimeter data fusion.

To further assess the global model performance in coastal regions, the difference between the global model and shipboard gravity was obtained in different ranges from the coastline, as shown in

Table 4. The difference between the global model and shipboard gravity in different ranges from the coastline (Unit: mGal).

Range Away from the Coastline(km)	DTU17		SDUST2021GRA		SIO V31.1
	Mean	RMS	Mean	RMS	Mean	RMS
[80, 100)	0.19	4.73	0.03	4.53	−0.03	4.86
[60, 80)	0.85	5.20	0.03	5.25	−0.03	4.97
[40, 60)	0.17	5.43	−0.12	5.22	0.07	5.06
[20, 40)	−2.09	7.72	−1.87	7.01	−1.90	7.72
[0, 20)	−1.84	9.65	−1.54	8.96	−0.21	8.90

. The coastline data were determined by the coast module in GMT [133].

Table 4 data indicate that the closer they are to the coastline, the lower the accuracy of all models. The main reason is that the number of altimeter data observations and the accuracy of each error correction gradually decrease when close to the coastline. Additionally, it is likely that the gravity calculation is less reliable near the edge of the data set. Although the assessment was affected by the shipboard gravity accuracy to a certain extent, it also indicated that the model accuracy in coastal areas must be improved, particularly within 40 km from the coastline.

6. Conclusions

The advancement of satellite altimetry techniques has considerably enhanced marine gravity field recovery. Altimetry missions with various altimeter operating modes, including LRM, SAR mode, laser altimetry, etc., have provided multiple sources of data that contributed greatly to improving the accuracy and resolution of the marine gravity anomaly model. The upcoming operation of the next-generation wide-swath interferometric altimetry SWOT mission is expected to significantly improve the resolution and accuracy of the gravity model. Altimeter data processing has been improved in terms of altimetry error correction, GM and ERM altimeter data processing, and multi-satellite altimeter data fusion, which also further enhances marine gravity field recovery, particularly in coastal and complicated sea surface regions. Methods based on vertical deflection data, such as the inverse Vening Meinesz formula and Laplace’s equation, are frequently utilized in marine gravity field recovery owing to their ability to attenuate residual errors in altimeter data. Thanks to the improvements in various aspects not limited to the abovementioned, the altimeter-derived global marine gravity field has an accuracy of about 4.00 mGal in low-middle latitude regions compared with shipboard gravity from NECI.

Marine gravity field recovery has been significantly enhanced, but it is imperative to establish a high-accuracy and high-resolution marine gravity field model to aid in understanding the mesoscale and microscale marine phenomena. Accordingly, the following suggestions are made for future marine gravity field recovery:

(1) Altimetry range corrections in coastal areas and complicated sea surface regions. Although altimetry range correction methods have advanced greatly in coastal areas, the correction accuracy is still lower than that in the open ocean. In addition, the waveform retracking, SSB correction, WTC, and tidal corrections are still considered the main sources of uncertainty in SSH observation. Accurate regional range corrections based on the characteristics of the regional sea surface are imperative to improve the quality of SSH observations;

(2) Multi-satellite altimeter data fusion. The accuracy of marine gravity field recovery can be further improved by multi-satellite altimeter data fusion, including ERM and GM data fusion, Ka-band and Ku-band altimeter data fusion, and different altimeter operating mode data fusion. For ERM and GM data, Ka-band and Ku-band altimeter data, it is important to consider how to make full use of the altimeter data based on their characteristics. Furthermore, how to benefit from several altimeter operating modes, including radar altimetry, laser altimetry, and swath interferometric modes altimetry, will be a challenge to marine gravity field recovery;

(3) Gravity anomaly solutions from vertical deflections. There is an imbalance in the accuracy of the meridian and prime components derived from vertical deflections, and determining the weights of the meridian and prime components for marine gravity field recovery is key. The upcoming altimetry mission (SWOT) will provide two-dimensional grid SSH data, and determining the precise vertical deflections will be a challenge;

(4) Optimization of the marine gravity field model based on the shipboard and airborne gravity measurements. In some areas, the accuracy of the marine gravity field model is low, and it is difficult to improve the accuracy of the model simply using altimeter data. High-accuracy gravity data are also provided by shipboard and airborne measurements. Integrating multiple types of gravity data is a critical issue.