SAR Image Simulation Based on Effective View and Ray Tracing
Abstract
:1. Introduction
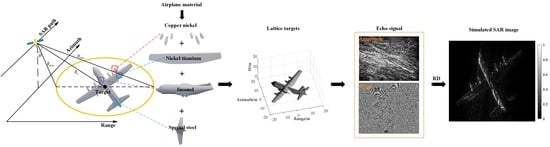
- An SAR effective view algorithm is designed to directly discretize the facets set in the SAR irradiated area into lattice targets. The algorithm adopts the idea of dual-scale subdivision and follows the SAR actual working system mode.
- A novel echo-based SAR image simulation method is proposed to improve the fidelity of simulated SAR images. The method provides a new research idea to combine the ray tracing algorithm and echo time-domain simulation. The method includes multiple scattering and records various kinds of backscatter coefficient for each point target within the synthetic aperture time.
- The proposed method is qualitatively and quantitatively evaluated with real scattering path analysis and structural similarity, respectively.
2. Target Model Latticing Using the SAR Effective View Algorithm
2.1. Construction of the Lattice Model
2.2. Calculation of the Lattice Coordinates
3. Echo Time-Domain Simulation and Imaging of Lattice Targets Based on Ray Tracing Algorithm
3.1. Improvement of the Illumination Model
- 1)
- The “stop-and-go” SAR signal mode is adopted.
- 2)
- The transmitting and receiving energy are located at the same position.
- 3)
- The actively transmitted microwave is the only energy source.
- 4)
- Multiple backscatter fields include the magnitude and phase.
- 5)
- The distance decay factor is added. The backscatter energy is inversely proportional to the 4th power of the propagation distance.
3.2. Setting of the Echo Time-Domain Simulation Model
3.3. Calculation of the Backscatter Field
- The sensor instantaneous position can be obtained by Equation (21). The initial incidence direction of the discrete electromagnetic waves can be provided by the lattice targets obtained by using the SAR effective view algorithm, with reference to Equation (30).
- After simulating the transmitted electromagnetic wave interactions with the target surface, the direction of specular reflection is calculated according to Fresnel’s law of reflection, as shown in Equation (31) for detail.
- The intersection of electromagnetic wave and target surface is used as the new starting point of incidence, and the specular reflection direction is used as the next new incidence direction to alternately complete multiple scattering of electromagnetic waves. The calculation of the single intersection coordinate of electromagnetic wave and target surface can refer to Equations (8)–(15) in detail.
- The termination conditions of multiple scattering are set according to the actual propagation path and energy decay of the electromagnetic wave. As the electromagnetic wave continues to track in the new reflection direction after each scattering, it still needs to traverse all the surface facets to find the location of the nearest collision point. If no collision occurs, the tracking of scattering path will end. After each scattering of the electromagnetic wave, the energy continues to decay, and the tracking of the scattering path will end when the energy decay threshold is met, with reference to Equation (32).
- Due to the complexity of the simulated targets or scenes, the multiple scattering intersections and the sensor location are not guaranteed to be through-view all the time. Therefore, it is necessary to add the through-view condition; that is, if there is a collision point, we transmit a ray from the collision point to the radar platform to see if there is any occlusion, and if so, the intersection of the -th scattering is not visible with the sensor, and the backscattering energy and phase of the point cannot be recorded.
- The intersection coordinate for the -th scattering of electromagnetic wave with the target surface can be obtained in turn using steps 1 to 5, and the instantaneous slant range of the -th scattering can be calculated by Equation (33):where is the instantaneous slant range of the -th scattering, which is equivalent to half the sum of the slant range from the sensor’s instantaneous position to the -th intersection point on the target. is the intersection coordinate for each scattering. is sensor’s instantaneous position, as shown in Equation (21) for detail. is the distance from the -th intersection coordinate on the target to the .
3.4. Generation and Imaging of the Echo Signal
- Range compression: The echo signal before and after range compression are shown in Figure 10c,d, respectively. The principle of stationary phase can be used to implement the range fast Fourier transform (FFT). When the echo signal is in the range frequency domain and the azimuth time domain, range compression can be performed by fast convolution. In particular, a matched filter should be designed to remove the second-order phase. Following the range FFT, the range-matched filter is performed immediately, and then the range compression is completed by using the range inverse Fourier transform (IFFT).
- Azimuth Fourier transform: The echo signal is transformed to the range-Doppler domain through the azimuth FFT, as shown in Figure 10e. Range cell migration correction is usually performed in the range-Doppler domain. In addition, Doppler centroid estimation and most subsequent operations are also performed in this domain.
- Range cell migration correction: As shown in Figure 10f, range cell migration correction is performed in the range-Doppler domain. Usually, in this domain, the trajectories of a group of targets in the same range cell coincide with each other. Mainly through interpolation processing based on the sinc function, the curve trajectory generated by the range cell migration correction can be straightened to be parallel to the azimuth frequency axis.
- Azimuth compression: After the range migration correction, the azimuth focusing of the echo signal can be carried out through the azimuth matched filter. In other words, azimuth compression is mainly achieved through azimuth matched filtering on each range cell, as shown in Figure 10g. Next, the echo signal is transformed to the 2D time domain through IFFT, and the result is the compressed complex image, as shown in Figure 10h.
4. Discussion of Simulation Results
4.1. Test Parameters and Models
4.2. Qualitative Analysis of the Test Results
4.3. Quantitative Analysis of the Test Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Holtzman, J.C.; Frost, V.S.; Abbott, J.L.; Kaupp, V.H. Radar image simulation. IEEE Trans. Geosci. Electron. 1978, 16, 296–303. [Google Scholar] [CrossRef]
- Chen, K.S. Principles of Synthetic Aperture Radar Imaging: A System Simulation Approach; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Brown, W.M. Synthetic aperture radar. IEEE Trans. Aerosp. Electron. Syst. 1967, AES-3, 217–229. [Google Scholar] [CrossRef]
- Franceschetti, G.; Migliaccio, M.; Riccio, D.; Schirinzi, G. SARAS: A synthetic aperture radar (SAR) raw signal simulator. IEEE Trans. Geosci. Remote Sens. 1992, 30, 110–123. [Google Scholar] [CrossRef]
- Franceschetti, G.; Marino, R.; Migliaccio, M.; Riccio, D. SAR simulation of three-dimensional scenes. In Proceedings of the Satellite Remote Sensing: SAR Data Processing for Remote Sensing, Rome, Italy, 26–30 September 1994. [Google Scholar]
- Franceschetti, G.; Guida, R.; Iodice, A.; Riccio, D.; Ruello, G.; Stilla, U. Simulation Tools for Interpretation of High Resolution SAR Images of Urban Areas. In Proceedings of the IEEE Urban Remote Sensing Joint Event, Paris, France, 11–13 April 2007. [Google Scholar]
- Horn, R. The DLR airborne SAR project E-SAR. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Lincoln, NE, USA, 31–31 May 1996. [Google Scholar]
- Boerner, E.; Uhlmann, F.H.; Grafmueller, B.; Zahn, R.; Braumann, H. SARIS: Synthetic aperture radar instrument simulator. In Proceedings of the Scanning the Present and Resolving the Future, Sydney, NSW, Australia, 9–13 July 2001. [Google Scholar] [CrossRef]
- Margarit, G.; Mallorqui, J.J.; Rius, J.M.; Marcos, J.S. On the Usage of GRECOSAR, an orbital polarimetric SAR simulator of complex targets, to vessel classification studies. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3517–3526. [Google Scholar] [CrossRef]
- Min, W.; Diannong, L.; Haifeng, H.; Zhen, D. SBRAS—An advanced simulator of spaceborne radar. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007. [Google Scholar]
- Dumont, R.; Guedas, C.; Thomas, E.; Cellier, F.; Donias, G. DIONISOS. An end-to-end SAR simulator. In Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010. [Google Scholar]
- Klaus, F. SiSAR: Advanced SAR simulation. In Proceedings of the Synthetic Aperture Radar and Passive Microwave Sensing, Paris, France, 25–28 September 1995; SPIE: Bellingham, WA, USA, 1995. [Google Scholar]
- Speck, R.; Hager, M.; Garcia, M.; Süß, H. An End-to-End-Simulator for Spaceborne SAR-Systems. In Proceedings of the European Conference on Synthetic Aperture Radar, Köln, Germany, 4–6 June 2002. [Google Scholar]
- Mori, A.; Vita, F.D. A time-domain raw signal Simulator for interferometric SAR. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1811–1817. [Google Scholar] [CrossRef]
- Allan, J.M.; Collins, M.J.; Gierull, C. Computational synthetic aperture radar (CSAR): A flexible signal simulator for multichannel SAR systems. Can. J. Remote Sens. 2010, 36, 345–360. [Google Scholar] [CrossRef]
- Drozdowicz, J. The Open-Source Framework for 3D Synthetic Aperture Radar Simulation. IEEE Access 2021, 9, 39518–39529. [Google Scholar] [CrossRef]
- Ilyushin, Y.A.; Orosei, R.; Witasse, O.; Sánchez, C.B. CLUSIM: A synthetic aperture radar clutter simulator for planetary exploration. Radio Sci. 2017, 52, 1200–1213. [Google Scholar] [CrossRef]
- Martino, G.D.; Iodice, A.; Poreh, D.; Riccio, D. Pol-SARAS: A Fully Polarimetric SAR Raw Signal Simulator for Extended Soil Surfaces. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2233–2247. [Google Scholar] [CrossRef]
- Franceschetti, G.; Iodice, A.; Riccio, D.; Ruello, G. SAR raw signal simulation for urban structures. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1986–1995. [Google Scholar] [CrossRef]
- Franceschetti, G.; Migliaccio, M.; Riccio, D. On Ocean SAR Raw Signal Simulation. IEEE Trans. Geosci. Remote Sens. 1998, 36, 84–100. [Google Scholar] [CrossRef]
- Franceschetti, G.; Lanari, R.; Marzouk, E.S. Two-dimensional squint mode SAR processing. In Proceedings of the Satellite Remote Sensing: SAR Data Processing for Remote Sensing, Rome, Italy, 26–30 September 1994. [Google Scholar]
- Franceschetti, G.; Iodice, A.; Riccio, D.; Ruello, G. SAR raw signal simulation of oil slicks in ocean environments. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1935–1949. [Google Scholar] [CrossRef]
- Franceschetti, G.; Iodice, A.; Riccio, D.; Ruello, G. Efficient hybrid stripmap/spotlight SAR raw signal simulation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004. [Google Scholar]
- Franceschetti, G.; Iodice, A.; Riccio, D.; Ruello, G. Efficient simulation of hybrid stripmap/spotlight SAR raw signals from extended scenes. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2385–2396. [Google Scholar] [CrossRef]
- Kaupp, V.H.; Waite, W.P.; Macdonald, H.C. SAR simulation. In Proceedings of the IGARSS ‘86: Remote Sensing: Today’s Solutions for Tomorrow’s Information Needs, Zuerich, Switzerland, 8–11 September 1986. [Google Scholar]
- Yoshida, T.; Rheem, C.K. Time domain simulation of ocean SAR image with wave and wind. In Proceedings of the IEEE Oceans, Yeosu, Korea, 21–24 May 2012. [Google Scholar]
- Chunyang, L.; Yongchang, J. SAR echo-wave signal simulation system based on MATLAB. In Proceedings of the IEEE 2012 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Shenzhen, China, 5–8 May 2012. [Google Scholar]
- Tao, J.; Auer, S.; Palubinskas, G.; Reinartz, P.; Bamler, R. Automatic SAR Simulation Technique for Object Identification in Complex Urban Scenarios. IEEE J. Select. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 994–1003. [Google Scholar] [CrossRef]
- Kai, W.; Jie, C.; Wei, Y.; Jian, Z. High accuracy SAR echo generation approach using space-time-variant backscatter characteristics. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014. [Google Scholar]
- Fan, Z.; Xiaojie, Y.; Hanyuan, T.; Qiang, Y.; Yuxin, H.; Bin, L. Multiple mode SAR raw data simulation and parallel acceleration for Gaofen-3 mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2115–2126. [Google Scholar] [CrossRef]
- Chengyen, C.; Kunshan, C.; Ying, Y.; Yang, Z.; Tong, Z. SAR Image Simulation of Complex Target including Multiple Scattering. Remote Sens. 2021, 13, 4854. [Google Scholar] [CrossRef]
- Qian, L.; Yanmin, Z.; Yunhua, W.; Yining, B.; Yushi, Z.; Xin, L. Numerical Simulation of SAR Image for Sea Surface. Remote Sens. 2022, 14, 439. [Google Scholar] [CrossRef]
- Dandan, W. Research on Target Simulation and Discrimination Technology of Wideband Radar. Bachelor’s Thesis, Xi Dian University, Xi An, China, 2020. [Google Scholar]
- Embrechts, J.J. Light scattering by rough surfaces: Electromagnetic model for lighting simulations. Light. Res. Technol. 1992, 24, 243–254. [Google Scholar] [CrossRef]
- The Phong Model, Introduction to the Concepts of Shader, Reflection Models and BRDF. Available online: https://www.scratchapixel.com/lessons/3d-basic-rendering/phong-shader-BRDF (accessed on 13 November 2019).
- Auer, S. 3d synthetic aperture radar simulation for interpreting complex urban reflection scenarios. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2011. [Google Scholar]



















| Parameter | SAR System1 | SAR System 2 |
|---|---|---|
| Model | Car body/Assault boat | Airplane |
| Signal form | Linear FM signal | Linear FM signal |
| Bandwidth | 50 MHZ | 180 MHZ |
| Pulse duration | 2.5 μs | 1.0 μs |
| Wavelength | 0.057 m | 0.020 m |
| Range sampling ratio | 60 MHZ | 190 MHZ |
| Range resolution | 3.0 m | 1.0 m |
| Incident angle | 60.00° | 59.92° |
| Center frequency | 5.3 GHZ | 15 GHZ |
| Platform height | 10 km | 2 km |
| Effective radar velocity | 400 m/s | 300 m/s |
| Doppler bandwidth | 125 HZ | 400 HZ |
| PRF | 200 HZ | 450 HZ |
| Slant range of scene center | 20 km | 4 km |
| Azimuth resolution | 3 m | 1 m |
| Squint angle | 0° | 0° |
| Material (Main Component) | Diffuse Coefficient | Specular Coefficient | Specular Index | Energy Decay Coefficient |
|---|---|---|---|---|
| Aluminum | 0.75 | 0.80 | 50.00 | 0.20 |
| Fiber reinforced plastics | 0.80 | 0.60 | 50.00 | 0.10 |
| Special steel | 0.65 | 0.80 | 30.00 | 0.25 |
| Copper nickel | 0.70 | 0.50 | 50.00 | 0.15 |
| Inconel | 0.75 | 0.40 | 30.00 | 0.10 |
| Nickel titanium | 0.65 | 0.70 | 40.00 | 0.20 |
| Normalized Cross-Correlation | Cosine Similarity | Mean Hash Similarity |
|---|---|---|
| 0.85 | 0.91 | 0.83 |
| CPU Specification | Model | SAR Image Size | Time (32-Threads) | |
|---|---|---|---|---|
| 12th Gen Intel (R) Core (TM)-i7-12900H-32G | Airplane | Azimuth | 378 samples | 0.63 h |
| Range | 429 samples | |||
| Aircraft Carrier | Azimuth | 1837 samples | 1.08 h | |
| Range | 1253 samples | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, K.; Jin, G.; Xiong, X.; Zhang, H.; Wang, L. SAR Image Simulation Based on Effective View and Ray Tracing. Remote Sens. 2022, 14, 5754. https://doi.org/10.3390/rs14225754
Wu K, Jin G, Xiong X, Zhang H, Wang L. SAR Image Simulation Based on Effective View and Ray Tracing. Remote Sensing. 2022; 14(22):5754. https://doi.org/10.3390/rs14225754
Chicago/Turabian StyleWu, Ke, Guowang Jin, Xin Xiong, Hongmin Zhang, and Limei Wang. 2022. "SAR Image Simulation Based on Effective View and Ray Tracing" Remote Sensing 14, no. 22: 5754. https://doi.org/10.3390/rs14225754
APA StyleWu, K., Jin, G., Xiong, X., Zhang, H., & Wang, L. (2022). SAR Image Simulation Based on Effective View and Ray Tracing. Remote Sensing, 14(22), 5754. https://doi.org/10.3390/rs14225754