High-Resolution Seamless Daily Sea Surface Temperature Based on Satellite Data Fusion and Machine Learning over Kuroshio Extension
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Satellite and In Situ Data
3. Methods
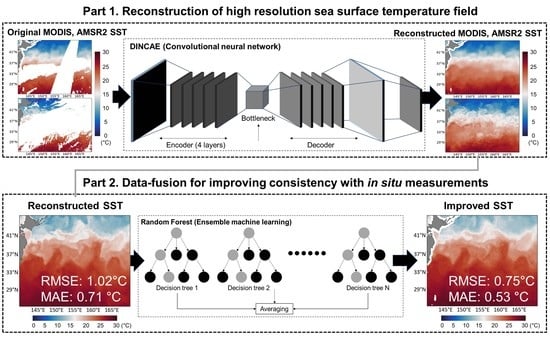
3.1. Reconstruction of SST
3.1.1. Data INterpolate Convolutional AutoEncoder (DINCAE)
3.2. Data Fusion for Improving Reconstructed SST
Random Forest (RF)
3.3. Performance Evaluation of the Proposed Approach
4. Results and Discussion
4.1. Performance of SST Reconstruction
4.2. Improvement of the Reconstructed SST
4.3. Feature Resolution Analysis
4.4. Novelty and Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dunstan, P.K.; Foster, S.D.; King, E.; Risbey, J.; O’Kane, T.J.; Monselesan, D.; Hobday, A.J.; Hartog, J.R.; Thompson, P.A. Global patterns of change and variation in sea surface temperature and chlorophyll a. Sci. Rep. 2018, 8, 14624. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, S.; Deser, C.; Alexander, M.A. Estimation of the surface heat flux response to sea surface temperature anomalies over the global oceans. J. Clim. 2005, 18, 4582–4599. [Google Scholar] [CrossRef] [Green Version]
- Podestá, G.P.; Glynn, P.W. Sea surface temperature variability in Panamá and Galápagos: Extreme temperatures causing coral bleaching. J. Geophys. Res. Ocean. 1997, 102, 15749–15759. [Google Scholar]
- Samelson, R.; Skyllingstad, E.; Chelton, D.; Esbensen, S.; O’Neill, L.; Thum, N. On the coupling of wind stress and sea surface temperature. J. Clim. 2006, 19, 1557–1566. [Google Scholar]
- Brasnett, B.; Colan, D.S. Assimilating retrievals of sea surface temperature from VIIRS and AMSR2. J. Atmos. Ocean. Technol. 2016, 33, 361–375. [Google Scholar] [CrossRef]
- Cummings, J.A. Operational multivariate ocean data assimilation. Q. J. R. Meteorol. Soc. 2005, 131, 3583–3604. [Google Scholar] [CrossRef] [Green Version]
- O’Carroll, A.G.; Armstrong, E.M.; Beggs, H.M.; Bouali, M.; Casey, K.S.; Corlett, G.K.; Dash, P.; Donlon, C.J.; Gentemann, C.L.; Høyer, J.L. Observational needs of sea surface temperature. Front. Mar. Sci. 2019, 6, 420. [Google Scholar] [CrossRef]
- Tory, K.J.; Dare, R.A. Sea surface temperature thresholds for tropical cyclone formation. J. Clim. 2015, 28, 8171–8183. [Google Scholar] [CrossRef]
- Vazquez-Cuervo, J.; Torres, H.S.; Menemenlis, D.; Chin, T.; Armstrong, E.M. Relationship between SST gradients and upwelling off Peru and Chile: Model/satellite data analysis. Int. J. Remote Sens. 2017, 38, 6599–6622. [Google Scholar] [CrossRef]
- Wentz, F.J.; Gentemann, C.; Smith, D.; Chelton, D. Satellite measurements of sea surface temperature through clouds. Science 2000, 288, 847–850. [Google Scholar] [CrossRef] [Green Version]
- Barth, A.; Beckers, J.-M.; Troupin, C.; Alvera-Azcárate, A.; Vandenbulcke, L. divand-1.0: N-dimensional variational data analysis for ocean observations. Geosci. Model Dev. 2014, 7, 225–241. [Google Scholar] [CrossRef] [Green Version]
- Barth, A.; Troupin, C.; Reyes, E.; Alvera-Azcárate, A.; Beckers, J.-M.; Tintore, J. Variational interpolation of high-frequency radar surface currents using DIVAnd. Ocean Dyn. 2021, 71, 293–308. [Google Scholar] [CrossRef]
- Beckers, J.-M.; Barth, A.; Alvera-Azcárate, A. DINEOF reconstruction of clouded images including error maps–application to the Sea-Surface Temperature around Corsican Island. Ocean Sci. 2006, 2, 183–199. [Google Scholar]
- Beckers, J.-M.; Rixen, M. EOF calculations and data filling from incomplete oceanographic datasets. J. Atmos. Ocean. Technol. 2003, 20, 1839–1856. [Google Scholar] [CrossRef]
- Chin, T.M.; Vazquez-Cuervo, J.; Armstrong, E.M. A multi-scale high-resolution analysis of global sea surface temperature. Remote Sens. Environ. 2017, 200, 154–169. [Google Scholar] [CrossRef]
- Donlon, C.J.; Martin, M.; Stark, J.; Roberts-Jones, J.; Fiedler, E.; Wimmer, W. The operational sea surface temperature and sea ice analysis (OSTIA) system. Remote Sens. Environ. 2012, 116, 140–158. [Google Scholar] [CrossRef]
- Fablet, R.; Viet, P.H.; Lguensat, R. Data-driven Models for the Spatio-Temporal Interpolation of satellite-derived SST Fields. IEEE Trans. Comput. Imaging 2017, 3, 647–657. [Google Scholar]
- Ouala, S.; Fablet, R.; Herzet, C.; Chapron, B.; Pascual, A.; Collard, F.; Gaultier, L. Neural network based Kalman filters for the Spatio-temporal interpolation of satellite-derived sea surface temperature. Remote Sens. 2018, 10, 1864. [Google Scholar] [CrossRef] [Green Version]
- Høyer, J.L.; Le Borgne, P.; Eastwood, S. A bias correction method for Arctic satellite sea surface temperature observations. Remote Sens. Environ. 2014, 146, 201–213. [Google Scholar] [CrossRef]
- Good, S.; Fiedler, E.; Mao, C.; Martin, M.J.; Maycock, A.; Reid, R.; Roberts-Jones, J.; Searle, T.; Waters, J.; While, J. The current configuration of the OSTIA system for operational production of foundation sea surface temperature and ice concentration analyses. Remote Sens. 2020, 12, 720. [Google Scholar] [CrossRef] [Green Version]
- Alvera-Azcárate, A.; Barth, A.; Parard, G.; Beckers, J.-M. Analysis of SMOS sea surface salinity data using DINEOF. Remote Sens. Environ. 2016, 180, 137–145. [Google Scholar] [CrossRef] [Green Version]
- Alvera-Azcárate, A.; Barth, A.; Beckers, J.M.; Weisberg, R.H. Multivariate reconstruction of missing data in sea surface temperature, chlorophyll, and wind satellite fields. J. Geophys. Res. Ocean. 2007, 112. [Google Scholar]
- Hilborn, A.; Costa, M. Applications of DINEOF to satellite-derived chlorophyll-a from a productive coastal region. Remote Sens. 2018, 10, 1449. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.; Khan, F.A.; Tian, H.; Liu, Q. Analysis of the monthly and spring-neap tidal variability of satellite chlorophyll-a and total suspended matter in a turbid coastal ocean using the DINEOF method. Remote Sens. 2021, 13, 632. [Google Scholar] [CrossRef]
- Barth, A.; Alvera-Azcárate, A.; Licer, M.; Beckers, J.-M. DINCAE 1.0: A convolutional neural network with error estimates to reconstruct sea surface temperature satellite observations. Geosci. Model Dev. 2020, 13, 1609–1622. [Google Scholar] [CrossRef] [Green Version]
- Jang, E.; Im, J.; Ha, S.; Lee, S.; Park, Y.-G. Estimation of water quality index for coastal areas in Korea using GOCI satellite data based on machine learning approaches. Korean J. Remote Sens. 2016, 32, 221–234. [Google Scholar] [CrossRef] [Green Version]
- Jang, E.; Kim, Y.J.; Im, J.; Park, Y.-G. Improvement of SMAP sea surface salinity in river-dominated oceans using machine learning approaches. GISci. Remote Sens. 2021, 58, 138–160. [Google Scholar] [CrossRef]
- Kumar, C.; Podestá, G.; Kilpatrick, K.; Minnett, P. A machine learning approach to estimating the error in satellite sea surface temperature retrievals. Remote Sens. Environ. 2021, 255, 112227. [Google Scholar] [CrossRef]
- Park, J.; Kim, J.-H.; Kim, H.-c.; Kim, B.-K.; Bae, D.; Jo, Y.-H.; Jo, N.; Lee, S.H. Reconstruction of ocean color data using machine learning techniques in Polar Regions: Focusing on Off Cape Hallett, Ross Sea. Remote Sens. 2019, 11, 1366. [Google Scholar] [CrossRef] [Green Version]
- Saux Picart, S.; Tandeo, P.; Autret, E.; Gausset, B. Exploring Machine Learning to Correct Satellite-Derived Sea Surface Temperatures. Remote Sens. 2018, 10, 224. [Google Scholar] [CrossRef] [Green Version]
- Stock, A.; Subramaniam, A.; Van Dijken, G.L.; Wedding, L.M.; Arrigo, K.R.; Mills, M.M.; Cameron, M.A.; Micheli, F. Comparison of cloud-filling algorithms for marine satellite data. Remote Sens. 2020, 12, 3313. [Google Scholar] [CrossRef]
- Sunder, S.; Ramsankaran, R.; Ramakrishnan, B. Machine learning techniques for regional scale estimation of high-resolution cloud-free daily sea surface temperatures from MODIS data. ISPRS J. Photogramm. Remote Sens. 2020, 166, 228–240. [Google Scholar] [CrossRef]
- Lee, J.; Kim, M.; Im, J.; Han, H.; Han, D. Pre-trained feature aggregated deep learning-based monitoring of overshooting tops using multi-spectral channels of GeoKompsat-2A advanced meteorological imagery. GISci. Remote Sens. 2021, 58, 1052–1071. [Google Scholar] [CrossRef]
- Pisoni, E.; Pastor, F.; Volta, M. Artificial Neural Networks to reconstruct incomplete satellite data: Application to the Mediterranean Sea Surface Temperature. Nonlinear Process. Geophys. 2008, 15, 61–70. [Google Scholar] [CrossRef]
- Han, Z.; He, Y.; Liu, G.; Perrie, W. Application of DINCAE to Reconstruct the Gaps in Chlorophyll-a Satellite Observations in the South China Sea and West Philippine Sea. Remote Sens. 2020, 12, 480. [Google Scholar] [CrossRef] [Green Version]
- Joh, Y.; Di Lorenzo, E.; Siqueira, L.; Kirtman, B.P. Enhanced interactions of Kuroshio Extension with tropical Pacific in a changing climate. Sci. Rep. 2021, 11, 6247. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S.; Hacker, P. Effect of mesoscale eddies on subtropical mode water variability from the Kuroshio Extension System Study (KESS). J. Phys. Oceanogr. 2007, 37, 982–1000. [Google Scholar] [CrossRef] [Green Version]
- Yang, P.; Jing, Z.; Sun, B.; Wu, L.; Qiu, B.; Chang, P.; Ramachandran, S. On the upper-ocean vertical eddy heat transport in the Kuroshio extension. Part I: Variability and dynamics. J. Phys. Oceanogr. 2021, 51, 229–246. [Google Scholar] [CrossRef]
- Donohue, K.; Watts, D.R.; Tracey, K.; Wimbush, M.; Park, J.H.; Bond, N.; Cronin, M.; Chen, S.; Qiu, B.; Hacker, P. Program studies the Kuroshio extension. Eos Trans. Am. Geophys. Union 2008, 89, 161–162. [Google Scholar] [CrossRef]
- Kawabe, M. Variations of current path, velocity, and volume transport of the Kuroshio in relation with the large meander. J. Phys. Oceanogr. 1995, 25, 3103–3117. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Tang, R.; Yu, Y.; Ji, F. Variability in the Sea Surface Temperature Gradient and Its Impacts on Chlorophyll-a Concentration in the Kuroshio Extension. Remote Sens. 2021, 13, 888. [Google Scholar] [CrossRef]
- Minnett, P.; Alvera-Azcárate, A.; Chin, T.; Corlett, G.; Gentemann, C.; Karagali, I.; Li, X.; Marsouin, A.; Marullo, S.; Maturi, E. Half a century of satellite remote sensing of sea-surface temperature. Remote Sens. Environ. 2019, 233, 111366. [Google Scholar] [CrossRef]
- Morak-Bozzo, S.; Merchant, C.; Kent, E.; Berry, D.; Carella, G. Climatological diurnal variability in sea surface temperature characterized from drifting buoy data. Geosci. Data J. 2016, 3, 20–28. [Google Scholar] [CrossRef] [Green Version]
- Brown, O.B.; Minnett, P.J.; Evans, R.; Kearns, E.; Kilpatrick, K.; Kumar, A.; Sikorski, R.; Závody, A. Modis Infrared Sea Surface Temperature Algorithm Algorithm Theoretical Basis Document Version 2.0; University of Miami: Miami, FL, USA, 1999; Volume 31. [Google Scholar]
- Kilpatrick, K.A.; Podestá, G.; Walsh, S.; Williams, E.; Halliwell, V.; Szczodrak, M.; Brown, O.; Minnett, P.; Evans, R. A decade of sea surface temperature from MODIS. Remote Sens. Environ. 2015, 165, 27–41. [Google Scholar] [CrossRef]
- Shibata, A. A change of microwave radiation from the ocean surface induced by air-sea temperature difference. Radio Sci. 2003, 38, 8063. [Google Scholar] [CrossRef]
- Gentemann, C.L.; Meissner, T.; Wentz, F.J. Accuracy of satellite sea surface temperatures at 7 and 11 GHz. IEEE Trans. Geosci. Remote Sens. 2009, 48, 1009–1018. [Google Scholar] [CrossRef]
- Imaoka, K.; Kachi, M.; Fujii, H.; Murakami, H.; Hori, M.; Ono, A.; Igarashi, T.; Nakagawa, K.; Oki, T.; Honda, Y. Global Change Observation Mission (GCOM) for monitoring carbon, water cycles, and climate change. Proc. IEEE 2010, 98, 717–734. [Google Scholar] [CrossRef]
- Gentemann, C.L. Three way validation of MODIS and AMSR-E sea surface temperatures. J. Geophys. Res. Ocean. 2014, 119, 2583–2598. [Google Scholar] [CrossRef]
- Donlon, C.; Minnett, P.; Gentemann, C.; Nightingale, T.; Barton, I.; Ward, B.; Murray, M. Toward improved validation of satellite sea surface skin temperature measurements for climate research. J. Clim. 2002, 15, 353–369. [Google Scholar] [CrossRef] [Green Version]
- Embury, O.; Merchant, C.J.; Corlett, G.K. A reprocessing for climate of sea surface temperature from the along-track scanning radiometers: Initial validation, accounting for skin and diurnal variability effects. Remote Sens. Environ. 2012, 116, 62–78. [Google Scholar] [CrossRef] [Green Version]
- Minnett, P.J.; Smith, M.; Ward, B. Measurements of the oceanic thermal skin effect. Deep Sea Res. Part II Top. Stud. Oceanogr. 2011, 58, 861–868. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.-A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
- Barth, A.; Azcárate, A.A.; Joassin, P.; Beckers, J.-M.; Troupin, C. Introduction to optimal interpolation and variational analysis. SESAME Summer Sch. Varna Bulg. 2008. [Google Scholar]
- Beckers, J.-M.; Barth, A.; Tomazic, I.; Alvera-Azcárate, A. A method to generate fully multi-scale optimal interpolation by combining efficient single process analyses, illustrated by a DINEOF analysis spiced with a local optimal interpolation. Ocean Sci. 2014, 10, 845–862. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Kim, H.-C.; Bae, D.; Jo, Y.-H. Data Reconstruction for Remotely Sensed Chlorophyll-a Concentration in the Ross Sea Using Ensemble-Based Machine Learning. Remote Sens. 2020, 12, 1898. [Google Scholar] [CrossRef]
- Chi, J.; Kim, H.-C. Retrieval of daily sea ice thickness from AMSR2 passive microwave data using ensemble convolutional neural networks. GISci. Remote Sens. 2021, 58, 812–830. [Google Scholar] [CrossRef]
- Cho, D.; Yoo, C.; Im, J.; Lee, Y.; Lee, J. Improvement of spatial interpolation accuracy of daily maximum air temperature in urban areas using a stacking ensemble technique. GISci. Remote Sens. 2020, 57, 633–649. [Google Scholar] [CrossRef]
- Gao, P.; Wu, T.; Ge, Y.; Li, Z. Improving the accuracy of extant gridded population maps using multisource map fusion. GISci. Remote Sens. 2022. [Google Scholar] [CrossRef]
- Pham, T.D.; Yokoya, N.; Nguyen, T.T.T.; Le, N.N.; Ha, N.T.; Xia, J.; Takeuchi, W.; Pham, T.D. Improvement of Mangrove Soil Carbon Stocks Estimation in North Vietnam Using Sentinel-2 Data and Machine Learning Approach. GISci. Remote Sens. 2021, 58, 68–87. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Dabrowski, T.; Lyons, K.; Nolan, G.; Berry, A.; Cusack, C.; Silke, J. Harmful algal bloom forecast system for SW Ireland. Part I: Description and validation of an operational forecasting model. Harmful Algae 2016, 53, 64–76. [Google Scholar] [CrossRef] [PubMed]
- Sutherland, J.; Walstra, D.; Chesher, T.; Van Rijn, L.; Southgate, H. Evaluation of coastal area modelling systems at an estuary mouth. Coast. Eng. 2004, 51, 119–142. [Google Scholar] [CrossRef] [Green Version]
- Nagy, H.; Lyons, K.; McGovern, J.; Pereiro, D.; Mamoutos, I.; Nolan, G.; Dabrowski, T. Recent Progress in Downscaled Local Ocean Forecast Models for Irish Maritime Users. In Proceedings of the 9th EuroGOOS International Conference, Brest, France, 3–5 May 2021. [Google Scholar]
- Winter, C.; Poerbandono, P.; Hoyme, H.; Mayerle, R. Modelling of Suspended Sediment Dynamics in Tidal Channels of the German Bight. Die Küste 2005, 69, 253–278. [Google Scholar]
- Kennedy, J.J.; Smith, R.; Rayner, N. Using AATSR data to assess the quality of in situ sea-surface temperature observations for climate studies. Remote Sens. Environ. 2012, 116, 79–92. [Google Scholar] [CrossRef]
- Kennedy, J.J. A review of uncertainty in in situ measurements and data sets of sea surface temperature. Rev. Geophys. 2014, 52, 1–32. [Google Scholar] [CrossRef]
- Merchant, C.J.; Embury, O.; Rayner, N.A.; Berry, D.I.; Corlett, G.K.; Lean, K.; Veal, K.L.; Kent, E.C.; Llewellyn-Jones, D.T.; Remedios, J.J. A 20 year independent record of sea surface temperature for climate from Along-Track Scanning Radiometers. J. Geophys. Res. Ocean. 2012, 117, C12013. [Google Scholar] [CrossRef] [Green Version]
- Le Menn, M.; Poli, P.; David, A.; Sagot, J.; Lucas, M.; O’Carroll, A.; Belbeoch, M.; Herklotz, K. Development of surface drifting buoys for fiducial reference measurements of sea-surface temperature. Front. Mar. Sci. 2019, 6, 578. [Google Scholar] [CrossRef] [Green Version]
- Alerskans, E.; Høyer, J.L.; Gentemann, C.L.; Pedersen, L.T.; Nielsen-Englyst, P.; Donlon, C. Construction of a climate data record of sea surface temperature from passive microwave measurements. Remote Sens. Environ. 2020, 236, 111485. [Google Scholar] [CrossRef]
- Wang, C.; Shu, Q.; Wang, X.; Guo, B.; Liu, P.; Li, Q. A random forest classifier based on pixel comparison features for urban LiDAR data. ISPRS J. Photogramm. Remote Sens. 2019, 148, 75–86. [Google Scholar] [CrossRef]










| Variable Type | Variable |
|---|---|
| Satellite data derived (MODIS/AMSR2) | - SST anomalies scaled by the inverse of the error variance (the scaled anomaly is zero when data are in an absence) |
| - Inverse of the error variance (zero when data are in an absence) | |
| - Scaled SST anomalies of the previous day | |
| - Inverse of error variance of the previous day | |
| - Scaled SST anomalies of the next day | |
| Inverse of error variance of the next day | |
| Auxiliary variables | - Longitude (scaled linearly between −1 and 1) |
| - Latitude (scaled linearly between −1 and 1) | |
| - Cosine of the day of the year divided by 365.25 | |
| - Sine of the day of the year divided by 365.25 |
| Hyper-Parameters | Options |
|---|---|
| Window of timeseries SST | 3 days (±3–7 days) |
| Epoch | 800–1000 (Stop with the lowest error) |
| Standard deviation of the noise | 1 (0.9–1.1) |
| Error standard deviation of the observations | 0.05 |
| Image (transposed convolutional layer) resize method in the decoder layers | Nearest neighbor |
| Pooling method in the decoder layers | Average |
| Number of convolution layers of the encoder and decoder | 4/4 (1–4) |
| Batch size | 64 (50–128) |
| Skip-connection between the encoder and decoder | 4 |
| Dropout rate during optimization | 0.3 |
| Number of filters for the encoder and decoder layers (from left to right for the encoder layers, and the opposite for the decoder layers) | 16/24/36/54 (16–128) |
| Dropout rate in the latent space | 0.2 (0.1–0.3) |
| Activation function for convolutional layers | Leaky ReLu |
| L2 regularization weight | 0.001 |
| Optimizer | Adam |
| Learning rate of step size in the optimizer | 1 × 10−3 |
| The exponential decay rate for the first moment (i.e., beta 1) in the optimizer | 0.9 |
| Variable Type | Variable |
|---|---|
| In situ data (Target variable) | - GTS drifting buoys |
| DINCAE outputs (MODIS/AMSR2, input variables) | - Estimated SST (Mean SST add with anomaly SST calculate from SST scaled by the inverse of the expected error variance and logarithm of the inverse of the expected error variance) |
| - Expected error standard deviation from the logarithm of the inverse of the expected error variance | |
| Auxiliary variables (Input variables) | - Latitude (Scaled linearly between −1 and 1) |
| - Sine of the day of the year divided by 365.25 | |
| - Presence of data (If value = 1, data are missing; otherwise, data are valid) |
| Satellite | The Number of Tiles | Coefficient of Determination (R2) | Bias (°C) | RMSE (°C) | rRMSE (%) | MAE (°C) | The Number of Data |
|---|---|---|---|---|---|---|---|
| MODIS | 1 | 0.98 | 0.01 | 1.12 | 7.72 | 0.79 | 321,128 |
| 2 | 0.98 | 0.08 | 1.10 | 6.57 | 0.81 | 298,132 | |
| 3 | 0.98 | −0.31 | 0.98 | 5.94 | 0.73 | 186,952 | |
| 4 | 0.98 | 0.04 | 0.76 | 3.17 | 0.53 | 526,838 | |
| 5 | 0.98 | 0.07 | 0.65 | 2.67 | 0.44 | 545,800 | |
| 6 | 0.98 | −0.18 | 0.69 | 2.85 | 0.50 | 479,770 | |
| AMSR2 | 1 | 0.99 | 0.43 | 0.85 | 5.83 | 0.66 | 471,262 |
| 2 | 0.99 | −0.24 | 0.78 | 5.42 | 0.61 | 566,431 | |
| 3 | 0.99 | 0.20 | 0.67 | 4.79 | 0.51 | 713,314 | |
| 4 | 0.99 | 0.11 | 0.50 | 2.17 | 0.38 | 664,447 | |
| 5 | 0.99 | 0.01 | 0.45 | 1.92 | 0.33 | 660,315 | |
| 6 | 0.99 | −0.00 | 0.38 | 1.63 | 0.30 | 781,999 |
| Satellite | Pixels | Coefficient of Determination (R2) | Bias (°C) | RMSE (°C) | rRMSE (%) | MAE (°C) | ARMAE | The Number of Data (N) |
|---|---|---|---|---|---|---|---|---|
| MODIS | Original SST pixels | 0.99 | −0.31 | 0.76 | 3.42 | 0.53 | 0.023 | 73,023 |
| Reconstructed SST pixels | 0.98 | −0.35 | 1.10 | 5.96 | 0.78 | 0.041 | 189,398 | |
| Total (i.e., original + reconstructed SST pixels) | 0.98 | −0.34 | 1.02 | 5.21 | 0.71 | 0.036 | 262,421 | |
| AMSR2 | Original SST pixels | 0.99 | −0.12 | 0.83 | 4.36 | 0.60 | 0.031 | 142,557 |
| Reconstructed SST pixels | 0.98 | −0.20 | 0.85 | 4.22 | 0.62 | 0.030 | 119,864 | |
| Total (i.e., original + reconstructed SST pixels) | 0.99 | −0.15 | 0.84 | 4.30 | 0.61 | 0.031 | 262,421 |
| SST | Validation Area (i.e., Pixels) | Coefficient of Determination (R2) | Bias (°C) | RMSE (°C) | rRMSE (%) | MAE (°C) | ARMAE | The Number of Data (N) |
|---|---|---|---|---|---|---|---|---|
| Scheme 1 | Original MODIS SST pixels | 0.99 | 0.04 | 0.74 | 3.31 | 0.51 | 0.022 | 73,023 |
| Scheme 1 | Reconstructed MODIS SST pixels | 0.98 | 0.02 | 1.05 | 5.70 | 0.74 | 0.039 | 189,398 |
| Scheme 2 | Original MODIS SST pixels | 0.99 | 0.04 | 0.58 | 2.61 | 0.41 | 0.018 | 73,023 |
| Scheme 2 | Reconstructed MODIS SST pixels | 0.99 | 0.00 | 0.80 | 4.35 | 0.57 | 0.030 | 189,398 |
| Scheme 2 (Calibration) | The entire study area | 1.00 | 0.00 | 0.09 | 0.46 | 0.04 | 0.002 | 262,421 |
| OSTIA | The entire study area | 0.99 | 0.05 | 0.52 | 2.65 | 0.32 | 0.016 | 262,421 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, S.; Yoo, C.; Im, J. High-Resolution Seamless Daily Sea Surface Temperature Based on Satellite Data Fusion and Machine Learning over Kuroshio Extension. Remote Sens. 2022, 14, 575. https://doi.org/10.3390/rs14030575
Jung S, Yoo C, Im J. High-Resolution Seamless Daily Sea Surface Temperature Based on Satellite Data Fusion and Machine Learning over Kuroshio Extension. Remote Sensing. 2022; 14(3):575. https://doi.org/10.3390/rs14030575
Chicago/Turabian StyleJung, Sihun, Cheolhee Yoo, and Jungho Im. 2022. "High-Resolution Seamless Daily Sea Surface Temperature Based on Satellite Data Fusion and Machine Learning over Kuroshio Extension" Remote Sensing 14, no. 3: 575. https://doi.org/10.3390/rs14030575
APA StyleJung, S., Yoo, C., & Im, J. (2022). High-Resolution Seamless Daily Sea Surface Temperature Based on Satellite Data Fusion and Machine Learning over Kuroshio Extension. Remote Sensing, 14(3), 575. https://doi.org/10.3390/rs14030575