The Role of Remote Sensing Data and Methods in a Modern Approach to Fertilization in Precision Agriculture

Abstract

The precision fertilization system is the basis for upgrading conventional intensive agricultural production, while achieving both high and quality yields and minimizing the negative impacts on the environment. This research aims to present the application of both conventional and modern prediction methods in precision fertilization by integrating agronomic components with the spatial component of interpolation and machine learning. While conventional methods were a cornerstone of soil prediction in the past decades, new challenges to process larger and more complex data have reduced their viability in the present. Their disadvantages of lower prediction accuracy, lack of robustness regarding the properties of input soil sample values and requirements for extensive cost- and time-expensive soil sampling were addressed. Specific conventional (ordinary kriging, inverse distance weighted) and modern machine learning methods (random forest, support vector machine, artificial neural networks, decision trees) were evaluated according to their popularity in relevant studies indexed in the Web of Science Core Collection over the past decade. As a shift towards increased prediction accuracy and computational efficiency, an overview of state-of-the-art remote sensing methods for improving precise fertilization was completed, with the accent on open-data and global satellite missions. State-of-the-art remote sensing techniques allowed hybrid interpolation to predict the sampled data supported by remote sensing data such as high-resolution multispectral, thermal and radar satellite or unmanned aerial vehicle (UAV)-based imagery in the analyzed studies. The representative overview of conventional and modern approaches to precision fertilization was performed based on 121 samples with phosphorous pentoxide (P₂O₅) and potassium oxide (K₂O) in a common agricultural parcel in Croatia. It visually and quantitatively confirmed the superior prediction accuracy and retained local heterogeneity of the modern approach. The research concludes that remote sensing data and methods have a significant role in improving fertilization in precision agriculture today and will be increasingly important in the future.

1. Introduction

The increasing need for food production due to population growth is the cause of the continuous intensification of agricultural production, which leads to higher yields of agricultural crops on existing agricultural land [1]. 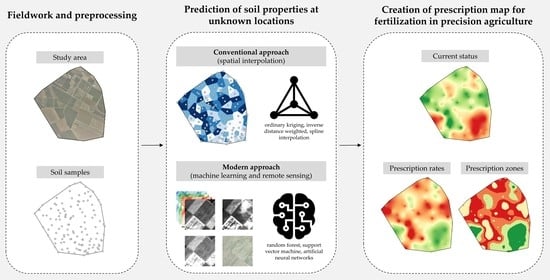Modern intensive agriculture makes fertilization one of the primary ways to achieve this goal; however, the short-term objectives of agricultural land management could seriously affect the long-term sustainability of food production [2]. Several authors have pointed out that farmers should not only consider fertilization with the aim of increasing their economic profits, but also in relation to maintaining the long-term biochemical soil composition and its effects on the ecosystem [3,4]. Poor management and understanding of fertilization itself have a significant negative impact on the environment, atmosphere, and natural resources, in addition to poor economic impacts on agricultural production [5]. The application of fertilizers in precision agriculture is an investment to increase the production potential of each plant within the agricultural parcel. This fact does not justify using a larger amount of fertilizer to achieve high yields, instead of achieving stable crop yields in an economical and efficient manner [6].

Fertilization in precision agriculture mainly ensures long-term optimal distribution of nutrients according to crop needs [7]. With technology development, conventional fertilization based on the average values of fertilizer applications within the agricultural land as a homogeneous unit is becoming obsolete. Instead, precision agriculture considers the agricultural parcel as a heterogeneous system, which is often very variable in its local spatial units [8]. Such an approach aims to balance the nutrients in the soil on the entire agricultural plot, so that all its parts enable optimal crop development [4]. Fertilization of agricultural crops is regularly performed in several iterations, following the current crop growth stage and the implementation of agrotechnical operations [9]. Basic fertilization involves the application of mineral and organic fertilizers before sowing, providing a sufficient amount of available nutrients in the soil to develop the plant root system. Supplementary fertilization allows for correcting the previously applied rates in basic fertilization, depending on the crop growth stage.

Spatial continuous data are crucial for making reliable prescription maps in precision fertilization. This property primarily refers to basic fertilization, where site-specific prescription zones form the basis of practical application based on discrete soil sampling [10]. Supplementary fertilization relies more heavily on indirect nutrient assessment in crops based on remote sensing, with soil sampling being used as a secondary spatial data source. Most of the collected data based on soil sampling are in a point vector format. To determine the continuous areas, it is necessary to estimate the values in non-sampled areas using spatial prediction methods [11]. A conventional postulate is that interpolation is one of the key components of data processing and analysis in the geographic information system (GIS) environment and is the subject of the study of statistics and geostatistics [12]. Interpolation is known as the process of deterministic or geostatistical prediction of the values of non-sampled areas, based on georeferenced soil samples to calculate a continuous surface. Papadopoulus et al. [13] stated that the key component in site-specific crop cultivation is geoinformation technologies, while agricultural land management depends on ecological and natural resources that have a spatial component. Geoinformation technologies are becoming a key factor in precision fertilization, as a basis for integrating discrete spatial data of soil sampling and their spatial prediction [4]. In addition to the direct application of spatial interpolation methods in precision fertilization, there is a successful long-term application in related soil-related activities.

Remote sensing data and methods were successfully implemented in various applications within precision agriculture [14,15,16,17]. Many authors have also used open and commercial satellite data for real-time monitoring of agricultural crops [16,18,19]. Earth observation satellites (e.g., PlanetScope) enable the daily monitoring of agricultural crops’ condition in large areas without going out into the field [20,21] and many authors give huge importance to developing fully automatic remote sensing methods that lead to complete automation of the satellite image-processing process [22,23]. In this way, end-users without advanced remote sensing knowledge can obtain a final product such as a weed map or soil moisture map automatically, almost in real-time. Remote sensing techniques based on machine learning algorithms can be used to predict and assess the physical and chemical parameters of the soil, which is extremely important for the fertilization process in precision agriculture [23,24,25], but although remote sensing data and methods are widely used in agriculture today, it is necessary to emphasize and exactly specify the importance of remote sensing applicability in the fertilization process. Since inadequate fertilization recommendations are directly affected by the inadequate choice of a spatial prediction method and input data [26], in the past few years, there has been a notable shift from the conventional interpolation methods to the modern approach based on machine learning (Figure 1). The number of scientific articles indexed in the Web of Science Core Collection (WoSCC) with the topic of “soil” combined with “fertilization” or “nutrient” and a particular prediction method rapidly increased during this period, and the remote sensing data have been as important as ever in soil prediction and precision fertilization studies. Their long-known importance as an abundant spatial data source has been further amplified by the application of machine learning methods to predict soil parameters, being one of the primary sources for covariates in these studies.

The main aim of this study was to investigate the ability of a modern machine learning approach supported by remote sensing for soil prediction in precision fertilization. Their relative prediction accuracy compared to conventional interpolation methods were investigated, as well as the conditions under which the cost-benefit and time-efficiency of soil sampling and the creation of a prescription map for fertilization are most affected. In accordance with the growing need and application of spatial prediction methods in precision fertilization, the specific objectives of this paper were to analyze, (1) the components of the integration of spatial prediction methods in the process of determining prescription rates in precision fertilization; and (2) the influence of modern remote sensing data and methods and their advantages according to the conventional approach in precision fertilization.

2. Integration of Geoinformation Technologies with Agronomic Principles of Precision Fertilization

Fertilization in precision agriculture is an inherently multidisciplinary approach, integrating the agronomic component of soil sampling and laboratory analysis with the spatial component of predicting soil parameters in a GIS environment (Figure 2). As the first step, soil sampling is intended to collect representative samples that will be used by chemical laboratory analysis to determine the state of soil nutrients. These generally consist of microelements and macroelements and other soil properties, such as soil pH, organic matter, and humus content. In addition to laboratory analysis, it is necessary to perform georeferencing of soil samples using global navigation satellite system (GNSS) positioning for further processing and interpretation of data for each sample [27]. De Zorzi et al. [28] stated that the spatial distribution of soil sampling depends on the area and geometrical properties of the agricultural parcel. The goal of the soil sampling is to collect the smallest possible number of representative samples that will not impair the accuracy of the spatial interpolation [29]. For this purpose, it is common to conduct preliminary zoning of agricultural plots before sampling, primarily by scanning the electrical conductivity of the soil. When sampling, it is important to choose the soil sampling depth, which depends on the type of crop and its root system, generally at two sampling depths, 0–30 cm and 30–60 cm.

By applying soil prediction methods, data from soil chemical analysis, GNSS observations and other relevant data are combined into one modular unit, representing a spatial distribution of the present state of available soil nutrients [30]. Such an approach enables observing local variability and creating prescription maps. For the prediction of soil properties at unknown locations, two main approaches are used: a conventional (based on geostatistical and deterministic interpolation methods) and a modern approach (based on machine learning) (Figure 3). After calculating the present state of a certain soil nutrient, areas of similar values are classified into several zones, with the aim of effective fertilizer application using agricultural machinery which supports precision fertilization [10]. Based on the current zones of nutrient status in the soil, the application zones for fertilization is calculated by subtracting the existing values from those prescribed by the agricultural expert [4]. Prescription maps are used to manage agricultural machinery as the final product of the whole process of computer processing. By exporting zoned prescription maps to the vector data format, the required amount of fertilizer for individual zones is defined. Among the included procedures, the selection of prediction methods and their parameters is a process in which the user has the highest subjective impact and dominantly determines the accuracy and reliability of the final prescription map [24]. Therefore, the two approaches to the prediction of soil properties in precision fertilization are analyzed in-depth in the following sections.

3. Conventional Approach to Fertilization in Precision Agriculture

Spatial interpolation to create a prescription map in precision fertilization is conventionally performed in 2D and based on prediction according to the values of neighboring samples and relative distance to them [31]. Due to a large number of methods, it is common to divide the spatial interpolation methods into two basic categories, namely, geostatistical and deterministic methods. In addition to interpolation, extrapolation is also used for irregular shapes of agricultural parcels to predict variables in locations outside the range of values covered by soil sampling. All methods of spatial interpolation can be represented by the weighted average of the sampled data according to Tobler’s first law of geography, according to which everything is related to everything else, but points that are closer to each other are strongly related [32]. In general, spatial interpolation methods share the same general Equation (1):

$${Z(x}_0)={{\displaystyle \sum }}_{i=1}^n{\lambda }_i{Z}_{x_i},$$

(1)

where ${Z(x}_0)$ represents the predicted value at the location, $x_0$_, n represents a total number of soil samples, $Z_{x_i}$ is the sampled value at the location i, while ${\lambda }_i$ is its respective weight. To select the most frequently used interpolation methods, the analysis using the annual number of published scientific studies was performed among the large number of available methods. According to the number of scientific papers indexed in the Web of Science Core Collection database between 2010 and 2020, the application of spatial interpolation methods, including conventional ones, is constantly growing (Figure 4). By searching for papers containing the topic keywords of “fertilization” and “agronomy” or “agriculture” in combination with the name of the spatial interpolation method, kriging, followed by the inverse distance weighted (IDW) and spline, deterministic methods were the most frequently used. Most of the analyzed methods implemented two or more spatial interpolation methods, which resulted in the higher sum of individual components than the total number of scientific papers.

The recent studies which utilized conventional interpolation methods for soil prediction in fertilization, sorted by the area of sampling sites, are presented in

Table 1. Studies which utilized a conventional interpolation method for soil prediction in fertilization.

Selected Soil Properties	Number of Samples (Study Area)	Country	Conventional Methods	R2 Accuracy Range	Reference
potassium	4266 (2,190,000 km2)	China	kriging with external drift	0.247–0.290	[38]
clay, silt, sand	1842 (34,151 km2)	France	CK, RK	0.460–0.780 (RK) 0.440–0.710 (CK)	[39]
SOC, pH, EC, bulk density	1044 (15,948 km2)	India	OK, IDW, EBK	0.928–0.941 (OK) 0.712–0.773 (IDW)	[40]
total nitrogen, phosphorous	259 (975 km2)	China	OK, RK	0.570–0.700 (RK) 0.510–0.680 (OK)	[41]
phosphorous, potassium	16,000 (245 km2)	Italy	OK	0.300–0.320	[42]
SOC	242 (141 km2)	China	OK, RK	0.166–0.263 (RK) 0.004–0.142 (OK)	[36]
pH, phosphorous, SOM	1004 (80.8 km2)	Croatia	IDW, OK, CK, spline	0.533–0.689 (OK) 0.504–0.672 (IDW)	[43]
phosphorous, potassium	160 (8.2 km2)	Croatia	OK, IDW	0.759–0.794 (IDW) 0.713–0.743 (OK)	[29]
total nitrogen	912 (1.9 km2)	China	GWR	0.670–0.925	[44]
phosphorous, potassium	296 (1.2 km2)	Croatia	OK, IDW	0.631–0.733 (OK) 0.400–0.693 (IDW)	[4]
pH, CEC, clay, EC, phosphorous, potassium	149 (0.2 km2)	Spain	OK	0.089–0.596	[33]
pH, EC, SOM, phosphorous, potassium	66 (0.003 km2)	Egypt	IK, PK	0.706 (PK) 0.533 (IK)	[34]

SOC: soil organic carbon, EC: soil electroconductivity, SOM: soil organic matter, CEC: cation exchange capacity, OK: ordinary kriging, CK: co-kriging, RK: regression kriging, EBK: empirical Bayesian kriging, IK: indicator kriging, PK: probability kriging, GWR: geographically weighted regression, IDW: inverse distance weighted.

. The interpolation accuracy was generally lower in study areas at the micro-level, which are highly common cases for precision fertilization [33,34]. Conventional interpolation methods were particularly unable to accurately predict and detect in-field variabilities in cases of lower spatial autocorrelation, which are a foundation of variable rate technology in precision agriculture [7]. According to Hengl [35], the higher spatial resolution necessary for small and moderately large agricultural parcels requires denser soil sampling in a conventional approach. This is a costly, labor- and time-expensive procedure, which disregards one of the purposes of precision agriculture. Furthermore, Radočaj et al. [29] proved that soil sampling density was a primary indicator of soil prediction accuracy using conventional interpolation methods. Mirás-Avalos et al. [33] observed a proportionally lower prediction accuracy of kriging with a larger distance from the nearest soil sample, resulting in unrealistic smoothing due to extrapolation, which is exaggerated for agricultural parcels with non-regular shapes. Reduced accuracy of conventional interpolation methods with a larger heterogeneity in soil types [33] and ineffective stratification [36] are the additional components which indicate a necessity for improving soil prediction performed by conventional interpolation methods [37].

The importance of selecting the optimal interpolation method and its parameters for fertilization in precision agriculture is manifested by avoiding poor agricultural practices and reducing the consumption of mineral and/or organic fertilizers. This directly impacts the financial savings in production and increases profits by achieving stable yields according to the local needs of crops. For these reasons, many previous studies have noted the importance of optimization of complete process prescription map creation in precision fertilization, which requires a multidisciplinary approach to obtain the desired result [45,46]. The selection of an optimal spatial interpolation method, and consequentially the prediction accuracy of soil parameters, depends on the properties of the input data set [47]. Therefore, there is no universally optimal spatial interpolation method, and multiple alternatives should be evaluated for each soil sample set [48].

The assessment of the accuracy of spatial interpolation methods is a necessary step for determining the optimal interpolation methods and parameters for the creation of a prescription map in precision fertilization [49]. Some of the most commonly used methods of the accuracy assessment of spatial interpolation results are the cross-validation and the split-sample methods. The cross-validation method is the most commonly used method of assessing the accuracy of interpolation methods and uses all sampled points to develop and compare models [50]. This method is also a suitable choice with a limited number of input values of soil samples, which is a very common case in agricultural land management conditions with smaller and fragmented agricultural parcels. The leave-one-out technique is the most common form of cross-evaluation, excluding each individual soil sample from the prediction and iteratively repeating the procedure for the number of input soil samples [51]. The reliability of this procedure particularly occurs for the high number of heterogenous soil sampling values. The split-sample method evaluates the prediction accuracy and robustness of the interpolation methods by splitting the input data into two parts based on a predefined ratio, forming training and test data [29]. The iteration of the procedure and repetitive accuracy assessment ensures the evaluation of consistency and robustness of the selected interpolation method.

Among the variety of statistical indicators of the interpolation accuracy, the coefficient of determination (R²) and the root-mean-square error (RMSE) are two of the most commonly used values [37], also enabling complementary accuracy assessment [52]. For the purpose of the accuracy assessment of predicted soil properties used in fertilization in precision agriculture, these are calculated according to Equation (2) and Equation (3) [47]:

$${\mathrm{R}}^2 = 1-\frac{{\mathrm{\sum }}_1^{\mathrm{n}}{({\mathrm{y}}_{\mathrm{i}}-{\widehat{\mathrm{y}}}_{\mathrm{i}})}^2}{{\mathrm{\sum }}_1^{\mathrm{n}}{({\mathrm{y}}_{\mathrm{i}}-{\overline{\mathrm{y}}}_{\mathrm{i}})}^2}$$

(2)

$$\text{RMSE}=\sqrt{\frac{{\mathrm{\sum }}_1^{\mathrm{n}}{({\mathrm{y}}_{\mathrm{i}}-{\widehat{\mathrm{y}}}_{\mathrm{i}})}^2}{\mathrm{n}}}$$

(3)

in which ${\mathrm{y}}_{\mathrm{i}}$ are the input sample values, ${\hat{\mathrm{y}}}_{\mathrm{i}}$ are the interpolated values, ${\overline{\mathrm{y}}}_{\mathrm{i}}$ is the average sample value, while n is the number of input samples. Besides their extensive application in conventional interpolation methods, these parameters are highly popular in evaluating the performance of the modern machine learning methods in soil mapping as well [53].

3.1. Geostatistical Spatial Interpolation Methods

The main feature of geostatistical methods is using variograms as a technique for quantifying and modelling continuous soil sampling values [54]. Unlike the classical deterministic approach, geostatistics considers the spatial dependence of variables, also known as spatial autocorrelation. Geostatistical interpolation methods assume that, by knowing the soil parameters at the sampled locations, it is possible to establish the relationship between these values and the distance from the unknown locations [55]. Although geostatistical methods in previous research have generally enabled a higher interpolation accuracy than deterministic methods, they require normal distribution and stationarity of soil sampling data [56]. In the absence of normal distribution of input data, the application of logarithmic transformation is recommended, which allows the implementation of kriging for such data sets [57]. While geostatistics is a straightforward concept, it includes several variations of kriging, which encompass the trends in soil sample data. Besides the spatial autocorrelation, particular multivariate kriging methods utilize independent predictors, unlike univariate methods. According to the number of scientific papers indexed in the Web of Science Core Collection database between 2010 and 2020, the most commonly used kriging methods are ordinary, regression, indicator, simple and universal kriging (Figure 5).

The variogram is used to quantify the spatial autocorrelation between sampling locations, by determining the relationship of sampled values according to their mutual distance [55]. The distance between the sampling locations is represented by h, and the value of the variogram concerning the h is known as a variance. If the values in a certain h deviate significantly from each other, meaning that their relationship has low spatial autocorrelation, then the variance is large. The semivariance (γ) of Z between the two sampling locations x_i and x₀ is a fundamental concept in geostatistics, defined by the expression [55] (4):

$$\gamma (x_i,x_0)=\gamma \left(h\right)=\text{var}⟦Z\left(x_i\right)-Z\left(x_0\right)⟧$$

(4)

To achieve an optimal interpolation result, it is necessary to fit a certain mathematical model to the variogram, represented by the highest possible coefficient of determination between the model and the variogram [58]. Each mathematical model is uniquely determined by nugget, sill, and range parameters. While nugget and sill indicate the shape of the selected mathematical model and its positioning relative to the y-axis, the range defines the maximum distance to neighboring soil samples until the presence of spatial autocorrelation is assumed. All soil samples located at the larger distances are considered spatially independent and do not affect predicted soil property values. Some of the most commonly used mathematical models are the linear, exponential, spherical, and Gaussian models [59].

3.2. Deterministic Spatial Interpolation Methods

IDW estimates the soil property values at unknown locations based on a weighted linear combination of the inverse distance function results per individual sampled locations. The deterministic function of IDW assumes that samples closer to the unknown location are proportionally more impactful, so the weight is represented by the expression [60] (5):

$${\lambda }_{i }=\frac{{1/h}_i^p}{{{\displaystyle \sum }}_{i=1}^n{1/h}_i^p},$$

(5)

where p represents power. The weight decreases as the distance and power parameter increase. The samples in the close neighborhood of the unknown location have a higher weight and thus a greater impact on the estimated value, resulting in local spatial interpolation. The power parameter and the neighborhood size are chosen arbitrarily, and the most common choice is the power parameter of 2 [61]. The higher p values decrease local heterogeneity and result in smoother areas, often resulting in lower interpolation accuracy when p is above 3.

The spline method belongs to the deterministic interpolation methods defined by polynomial curves [62]. Polynomials are used to describe parts of a line or surface, based on a small number of points, which results in the smooth surface by their mutual join. When choosing the p, the curve takes a linear, square or cubic shape, depending on whether the value of p is 1, 2 or 3, respectively. The third-degree cubic curves are most commonly used [63]. The linear spline interpolation method is often used to fill data gaps in tables and is much simpler than the cubic method. Additionally, if there are two spatial dimensions, it is considered a bi-linear method, and in the case of the third dimension, three-linear. Spline results in higher interpolation accuracy on surfaces with a less pronounced local variability, so they are not suitable for use in highly heterogenous or extreme cases, especially for smaller areas [64].

4. Modern Approach to Fertilization in Precision Agriculture

Over the past decade, the development of new technologies and sensors and sensor minimization has led to the development and improvement of the soil mapping and fertilization process in precision agriculture. Both soil prediction methods based on machine learning and remote sensing data are increasingly utilized in such studies, as presented in

Table 2. An overview of prediction methods and remote sensing data utilized in recent studies based on digital soil mapping.

Soil Properties	Prediction Methods	Multispectral/ Hyperspectral Images	DEM/ Radar Images	Reference
SOC, pH, sand, silt, clay, bulk density, CEC, coarse fragments	regression kriging, multiple linear regression, multinomial logistic regression	MODIS	SRTM	[65]
SOC, pH, sand, silt, clay, bulk density, CEC, coarse fragments	random forest, gradient boosting, neural networks	MODIS	SRTM	[66]
clay, silt, gravel, pH, SOM, bulk density, effective CEC	random forest, boosted regression trees	Landsat 7, SPOT5	custom DEM	[67]
SOC, pH, clay, CEC	multiple linear regression, regression kriging	/	custom DEM	[68]
nitrogen, phosphorous, boron	random forest, cubist model	Landsat 8	custom DEM	[69]
SOM, pH, SOC, total nitrogen, phosphorous, potassium	random forest, artificial neural network, co-kriging	GF-2	SRTM	[30]
SOC, sand, CCE	random forest, cubist model	Landsat 8	Alos AW3D	[70]
SOC	random forest, artificial neural networks, multiple linear regression	Landsat 8	ASTER	[71]
SOC, sand, silt, clay, pH, calcium, potassium, nitrogen, phosphorous, etc.	two-scale ensemble machine learning	Sentinel-2, Landsat 8, MODIS, PROBA-V, SM2RAIN	Sentinel-1, AW3D	[72]
SOC, total nitrogen, pH, sand, silt, clay, bulk density, CEC, coarse fragments	recursive feature elimination, quantile random forest	Landsat 8, MODIS	EarthEnv-DEM90	[73]
SOC, bulk density	partial least square regression, extreme learning machine	Sentinel-2, Landsat 8, Headwall-Hyperspec	/	[74]
SOM	random forest	Sentinel-2	custom DEM	[75]

SOC: soil organic carbon, SOM: soil organic matter, CEC: cation exchange capacity, CCE: calcium carbonate equivalent, SRTM: Shuttle Radar Topography Mission.

.

4.1. Remote Sensing Data

Novel multispectral and hyperspectral cameras on various platforms, from satellites to drones, enable high spatial and spectral remote sensing data that can be used in continuous agricultural field monitoring. Furthermore, with the development of Synthetic Aperture Radar (SAR; e.g., Sentinel-1) and optical satellite missions (e.g., Sentinel-2, PlanetScope), the Earth’s surface can be observed in high spatial resolution almost on a daily basis [76]. Satellite missions, but also new platforms such as unmanned aerial vehicles (UAVs) have led to the development and improvement of the quality of digital terrain models (DTM) and other important data in precision agriculture, e.g., the canopy height model (CHM). The development of remote sensing technologies and data lead to an increased application in precision agriculture. In the past few years, an increasing number of scientific articles in the field of remote sensing data in precision fertilization have been noted (Figure 6). A significant increase in the use of multispectral, hyperspectral and radar data is present, while the data on digital terrain models in precision fertilization are not growing at such a rate. Although the numbers of research with satellite data are significantly higher than the data obtained by UAV, a rapid growth in UAV application in the last five years has occurred. As in previous research [77], the prevalence of multispectral images is still higher than for radar. With the development of radar imaging technologies [78,79,80,81], mainly in soil moisture assessment, a significant increase in the number of studies in this area in the coming years is expected.

The above-mentioned remote sensing technology and sensors enable fast and accurate acquisition of the earth surface data. This data can describe the earth’s surface with 3D (e.g., digital elevation models, digital surface model) or in the 2D data type (e.g., spectral bands, composites) acquired by sensors located on various platforms, e.g., satellite, airplane, or UAV. The acquired data can be used to produce various crucial remote sensing data such as [82]:

(1)

various indices for an improved description of the earth’s surface (e.g., water, vegetation, soil) based on multispectral images or

(2)

various derivatives of the digital elevation models such as slope, curvature, or flow accumulation analysis.

Radar images must be emphasized while they find their application in detecting the amount of moisture in the soil [78,81], which is extremely important in precision agriculture. For example, the most used remote sensing data in precision fertilization for the exact location is shown in Figure 7.

4.2. Modern Remote Sensing Methods for Optimal Fertilization in Precision Agriculture

In the recent research [8,14,24,83,84,85], remote sensing methods for assessing precision agriculture and fertilization are divided into two different approaches:

(1)

Multivariate regressions based on various remote sensing data and

(2)

Machine and deep learning methods for predictions.

For many years, authors have used multivariate regressions to model the variables in precision agriculture [83,86]. With the development of remote sensing data, authors have introduced new measurements collected using remote sensing data [83] into the process of multivariate regressions. These data have greatly improved the process of estimating the required variables to create better and more productive crops [87]. Multivariate regressions based on various remote sensing data have greatly improved the estimates of soil parameters for precision fertilization in regards to the conventional spatial interpolation methods.

In the last decade, hardware and computer development have enabled and popularized the application of and development of advanced methods for processing large amounts of spatial data, such as machine learning and deep learning methods [88,89,90,91]. Nowadays, these methods are also often used in remote sensing to quickly and accurately classify large amounts of satellite images to obtain land use and land cover (LULC) maps of the earth’s surface [92,93]. The great importance of the machine and deep learning method lies in the rapid processing of various spatial and attribute data to improve the estimation and prediction of the variable, e.g., estimation of the fertilizer in crops from available satellite images [14,94,95]. Trends of the application of remote sensing methods in precision fertilization based on the research papers in the last decade are shown in Figure 8. Application of the random forest and support vector machine algorithm have shown an increasing trend during the previous five years, while the artificial neural network and decision tree methods applications have stagnated in precision fertilization.

Despite the existing conventional modern remote sensing methods, developing novel hybrid approaches would significantly improve the fertilization process in precision agriculture. Novel hybrid approaches would enable better spatial resolution and more accurate crop and soil conditions assessment, thus improving the fertilization process. The preliminary proposal of a novel hybrid approach is based on remote sensing data such as for vegetation, water and soil spectral indices, a digital elevation model and other remote sensing data (e.g., spectral bands) supported by raster data obtained by conventional spatial interpolation methods. Machine learning methods could quickly and accurately model all the mentioned data based on which of the above can be realized into a real and accurate prediction of the state of crops and soil.

5. A Representative Overview of Modern and Conventional Approaches for Fertilization in Precision Agriculture

To provide a more insightful overview of the efficiency of conventional and modern approaches to precision fertilization beyond the scientific review, a case study for a common agricultural parcel in Croatia was performed. Phosphorous pentoxide (P₂O₅) and potassium oxide (K₂O) were used for the prediction, representing two of the most important soil properties in agricultural fertilization [96]. A total of 121 samples were used in the agricultural parcel of 4.1 km², representing a micro-location such as in [29,44]. The descriptive statistics of the input soil sample set is presented in

Table 3. The descriptive statistics of the representative soil sample set used for the comparison of conventional and modern approaches to precision fertilization.

Soil Property	Average (mg 100 g–1)	Value Range (mg 100 g–1)	CV	SK	KT	Shapiro–Wilk Test		Moran’s I
						W	p
phosphorous pentoxide (P2O5)	23.2	8.9–41.0	0.364	0.587	–0.592	0.941	0.0005	0.209
potassium oxide (K2O)	26.1	17.2–50.5	0.253	1.517	3.092	0.877	< 0.0001	0.124

CV: coefficient of variation, SK: skewness, KT: kurtosis.

. All predicted results were calculated in a spatial resolution of 30 m, according to the specifications of Hengl [35]. Soil prediction accuracy was assessed using R² and RMSE, as the most commonly applied interpolation metrics in similar previous studies. The cross-validation using the leave-one-out technique was used for the accuracy assessment.

OK, as the most commonly applied geostatistical interpolation method, along with IDW, its deterministic counterpart, were used for the representation of the conventional prediction methods in fertilization. As the range of the OK interpolation is conditioned by spatial autocorrelation of the input values, some of the most commonly used mathematical models in previous studies were evaluated, as the primary parameter of the OK interpolation. Analogously, the most common power parameters of the IDW were evaluated. Due to the lack of data normality, a logarithmic transformation was performed in the preprocessing to OK interpolation.

Comparative displays of interpolation results produced by conventional interpolation methods for P₂O₅ and K₂O on the representative soil sample set are shown in Figure 9 and Figure 10. The interpolation results for both soil properties indicated a strong dependence of the prediction accuracy on the input parameters, indicating the importance of evaluating multiple methods, as well as their parameters, as noted in [47]. The R² of the OK ranged from 0.331 to 0.414 for the P₂O₅ and from 0.082 to 0.120 for the K₂O, indicating a proportionally lower accuracy for the input values with lower spatial autocorrelation, which is one of the main constraints of its prediction accuracy [97]. Due to its deterministic nature, IDW was resistant to this property, with its interpolation accuracy ranging from 0.233 to 0.405 for the P₂O₅ and from 0.234 to 0.374 for the K₂O. It generally produced a lower accuracy but with a more balanced approach regarding sensitivity to the input values, as noted in [29]. Besides varying the interpolation accuracy, the resulting value ranges and CV values were severely affected by the selection of the interpolation method and its parameters.

A total of twelve relevant covariates for the P₂O₅ and K₂O prediction used as the basis of the modern prediction approach are presented in

Table 4. Covariates used for the modern prediction using the representative soil sample set for precision fertilization.

Data Source	Environmental Segment	Covariate	Reference
digital elevation model (EU-DEM v1.1)	morphometry	slope	[99]
		aspect
		total curvature
		convergence index
	hydrology	flow accumulation	[100]
		topographic wetness index	[101]
multispectral satellite images (Landsat 8, sensed on 15th September 2021)	vegetation	normalized difference vegetation index (NDVI)	[102]
		enhanced vegetation index (EVI)	[103]
		normalized green-red vegetation index (NGRDI)	[104]
	soil	normalized difference soil index (NDSI)	[105]
		brightness index (BI)	[106]
	moisture	normalized difference moisture index (NDMI)	[107]

. These were defined with accordance to the specifications of soil mapping by Hengl and MacMillan [98] and which were used in similar soil prediction studies recently [66,73,82]. Six covariates were derived from a digital elevation model and six from Landsat 8 images, fully based on freely and widely available data. These covariates for the area covering the representative soil sample set are visually represented in Figure 7. Four of the most commonly applied machine learning methods in previous studies indexed in the WoSCC were used: random forest (RF), support vector machine (SVM), artificial neural networks (ANN) and decision tree (DT). These methods gained popularity in the modern approach to fertilization recently, allowing the integration of big data, that is highly accurate and with a computationally efficient prediction [53].

A comparative display of the modern soil prediction approach for fertilization in precision agriculture, along with the most accurate results of the conventional approach are displayed in Figure 11. Besides an improved prediction accuracy and resistance to the particular properties of input sample values, the modern approach included more soil heterogeneity in the result with higher CV values. Previous studies have also noted a superior prediction accuracy of the modern approach compared to conventional methods, especially in the cases of lower spatial autocorrelation indicated by high nugget values [38]. Besides the spectral indices and topographic indicators, which are applicable at both minor- and major-scales [82], climate data and auxiliary soil information are commonly included in the modern approach [73]. These values are generally more suitable for the macro-location studies due to their local homogeneity, as well as the lack of available spatial data at the higher spatial resolution to match those of satellite images and DEMs [2]. Despite the same spatial resolution of the P₂O₅ and K₂O rasters produced by the conventional and modern approaches, modern machine learning methods have resulted in much less smooth areas, retaining specific local information about field conditions, which are a backbone for precision agriculture [7]. Chen et al. [37] noted the improved spatial resolution as one of the key advantages of the modern approach over the conventional interpolation methods, alongside improved prediction accuracy and time- and cost-efficiency.

6. Conclusions

Fertilization is the foundation of agricultural production, which must be performed efficiently and in accordance with local crop needs to ensure sustainability and prevent soil degradation. Digitization of the entire procedure, from the collection of field data to the computer processing and production of a fertilization prescription map, is the basis of fertilization in precision agriculture. Management information systems are becoming critical in precision fertilization, and for such reasons, their importance inevitably becomes a priority. Technological progress leads to the development of more sophisticated and more accessible software packages that particularly segment the processing and application of spatial data. Modern fertilization relies on the use of agricultural information technology at an increasing level, which is a rapid development in agricultural practice, which now requires the constant learning and training of users and investment in new technological systems. Interpolation methods used for the purpose of precision fertilization play a very important role in the decision-making process and use of sampled data. Each of the methods described in this paper includes a certain level of uncertainty, but knowledge of their capabilities and utility enables the user to select an optimal method and its parameters to ensure maximum prediction accuracy. The further implementation of spatial interpolation methods in agricultural practice is expected to accelerate the transition from conventional intensive agriculture to precision agriculture, enabling stable yields and sustainable agricultural production in the future.

Modern remote sensing data improve the fertilization process in precision agriculture, as an abundant and freely accessible global data source. Radar and optical satellite imagery has allowed significant advances in cropland monitoring (e.g., soil moisture, phosphorous pentoxide) on a daily basis, while on the other side, UAVs equipped with novel hyperspectral and multispectral cameras enable the monitoring of crops at a centimeter-level. New radar imagery and satellite or UAV-based thermal imagery enables the development of novel algorithms and methods for obtaining crop and soil status. The novel, hybrid methods for modelling crop and soil quality improve the standard conventional and modern machine learning approaches. They also enable the computationally efficient and accurate integration of remote sensing data and achievements in precision agriculture and would also significantly improve the fertilization process. Novel hybrid approaches would enable a better spatial resolution and more accurate crop and soil conditions assessment. The application of earth observation satellites (e.g., PlanetScope) enables daily soil and crop status monitoring without going out into the field and novel, robust and automatic remote sensing methods will lead to the complete automation of the satellite image-processing process. This will enable end-users, without any remote sensing knowledge, to obtain a final product such as a weed map or soil moisture map automatically, almost in real-time.

Accordingly, it can be concluded that remote sensing data and methods now have a crucial role in the fertilization process in precision agriculture, and their importance is expected to increase in the future.