1. Introduction
In the GNSS/INS integrated system, INS is an autonomous navigation system that relies on airborne equipment to complete navigation tasks autonomously [
1,
2,
3]. However, the accumulation of position errors over time leads to poor accuracy. GNSS can obtain stable solutions in an open-sky environment, but its accuracy is severely reduced in the urban canyon with high-rise buildings, inside tunnels and under dense tree canopies [
4]. Therefore, combining the above two systems together can effectively leverage their respective advantages to form a navigation system with long-term stability, self-restraint, and high-frequency output [
3,
4,
5,
6]. Regarding the integration of GNSS/INS, the most common mode is the loosely coupled (LC) mode [
7]. The implementation of LC mode is relatively simple, but in the case of GNSS it must be receiving more than four satellites. However, the tightly coupled (TC) method is to directly fuse the GNSS raw output observations with the INS output, so the tightly coupled mode can still provide GNSS signal updates when fewer than four satellites are received [
8].
The TC integrated system can obtain better positioning accuracy in harsh environments. At this time, satellite signals may be blocked, making the statistical characteristics of measurement noise uncertain and time-varying. Inaccurate estimation of measurement noise covariance causes filter divergence [
9]. A TC integration system uses the GNSS raw observation data (pseudorange and pseudorange rate measurements) as a reference to evaluate and correct the INS error [
10]. For the measurement noise covariance in a tightly coupled integrated navigation system, traditional methods generally assume that it is a fixed a priori constant value, but it cannot truly represent the actual statistical characteristics of the measurement noise during actual operation. In actual navigation system applications, in order to be able to deal with the instability of the measurement noise covariance matrix [
11], the adaptive Kalman filter (AKF) that can estimate R online should be used to ensure the positioning accuracy and continuity of the navigation results [
12].
In recent years, deep learning domain knowledge has been widely used in natural language processing and computer vision [
13]. These methods discover complex structures through specific backpropagation and error correction mechanisms to instruct the machine how to change its internal parameters for learning features. Because a neural network has an ability to learn data relationships, for this article a neural network algorithm was designed in the TC integrated system. The algorithm can automatically learn the measurement noise parameters online and make adaptive adjustments according to the actual environment, so that the Kalman filter can perform accurate position estimation.
Conventionally, due to the inaccurate statistical characteristics of noise, the model cannot reflect the real physical process, so the observed values do not correspond to the model, which in turn leads to filter divergence [
14]. In practical application scenarios, it is inaccurate to assume that the noise is fixed. Therefore, adaptively adjusting the statistical characteristics of noise for different actual environments is more in line with the navigation process and improves the positioning performance in challenging environments.
For solving the problem of noise covariance estimation in the GNSS/INS integrated system, various adaptive adjustment methods have been developed in different scenarios [
15]. Cho and Choi combined Sigma-point KF (SPKF) with a receding-horizon strategy to propose a new filtering scheme that is beneficial for reducing initial estimation error and temporal unknown bias [
16]. Gao et al. [
17] proposed a strategy of seam tracking monitoring, in which the Sage–Husa AKF is given to estimate the statistical characteristics of noise, and the filter parameters are adjusted to achieve an adaptive ability in the case of noise changes. He et al. [
18] proposed a method to estimate the covariance matrix of measurement noise using a simplified Sage–Husa filter. Meng et al. [
15] presented an adaptive unscented Kalman filter (UKF) with a noise statistic estimator to make up for some of the shortcomings of the standard UKF.
Furthermore, covariance matching technology uses innovative covariance or residual covariance to reasonably estimate the covariance of the process noise and measurement noise at each sampling moment [
19]. When the statistical characteristics of noise need to be estimated, using the IAE method to estimate the covariance reduces the navigation accuracy, and even causes a risk of filtering divergence [
20]. In response to this problem, Zhang et al. [
21] proposed an INS/GNSS integrated navigation system adaptive estimation (RMAE) method based on redundant measurements, which uses the INS solution as redundant measurements to estimate the measurement noise covariance matrix. Due to the advantages of this aspect, in order to solve the coupling problem of estimating the measurement value and the process noise covariance at the same time, Ge et al. [
22] proposed a scheme combining the RMAE method with the estimation algorithm of process noise covariance. To improve the position accuracy and reliability, Ge et al. [
23] proposed a strategy for the mitigation of GNSS measurement disturbances in which the time-varying covariance of measurement noise is estimated by RMAE and Burg methods according to the statistical characteristics of the difference sequences. Sun et al. [
24] proposed a pseudorange error prediction method based on an ensemble bagged regression tree that updates the measurement noise covariance for tightly coupled GNSS/IMU navigation systems in urban areas. Ding et al. [
25] combined Bayesian inference methods with unscented Kalman filters to propose a new algorithm for estimating aerodynamic parameters and noise in aircraft dynamical systems. Bao et al. [
26] established an adaptive maneuvering target-tracking method using the interactive multiple method (IMM) for maneuver identification, and, at the same time, introduced the Sage–Husa adaptive filtering algorithm to estimate the measurement noise covariance in real time.
Due to the powerful data representation capabilities of neural networks in computer vision and natural language processing, there have been some methods combining neural networks with KF to improve the positioning accuracy of INS/GNSS integrated navigation systems. Haarnoja et al. [
27] designed a neural network suitable for state estimation by using covariance matrices to convey the expected degree of uncertainty in observations. Liu et al. [
28] introduced deep inference for covariance estimation (DICE) to predict the covariance of a sensor measurement from raw sensor data. The model restricts covariance predictions to positive definite values using a deep convolutional neural network to learn a noise model of sensor measurements. Coskun et al. [
29] proposed the LSTM Kalman filter (LSTM-KF), a new architecture which can learn the motion model and all noise parameters of the Kalman filter, thus allowing us to train our models with less data successfully. In the LC integrated navigation system, Gao et al. [
30] introduced reinforcement learning to estimate the process noise covariance adaptively. The algorithm takes the navigation system as the environment, takes the negative value of the positioning error as the reward and uses the deep deterministic policy as the gradient to obtain the optimal estimation. Wu et al. [
31] proposed an algorithm based on a multi-task learning model, which can estimate the processing noise covariance and measurement noise covariance of a Kalman filter simultaneously.
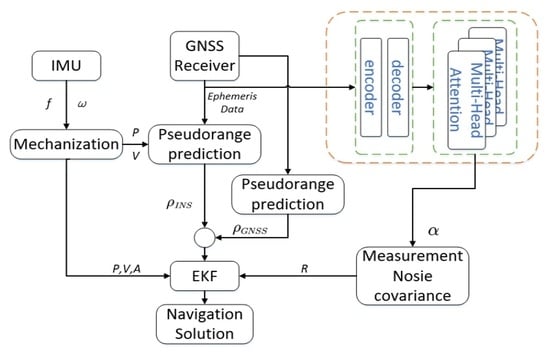
We propose a transformer-based noise covariance prediction model, which exploits an attention mechanism to learn the uncertainty of current raw satellite observations, and combines it with a Kalman filter to adaptively adjust the measurement noise covariance. Before the data enters the transformer network model, we use the residual denoising autoencoder (RDAE) to filter the original data. This method can make the model obtain better generalization ability, and make the task of adaptive adjustment of measurement noise covariance better. We conducted extensive experiments on practical road test data to evaluate our proposed navigation algorithm. Experimental results indicate that our proposed method is superior to the traditional algorithm of adjusting the covariance matrix of measurement noise, and obtains the best performance in comparison with other networks.
The remainder of this paper is organized as follows:
Section 2 briefly introduces the INS/GNSS tightly coupled integrated system and our proposed algorithm;
Section 3 demonstrates and presents an analysis of the algorithm based on actual road tests;
Section 4 discusses the experimental results; and
Section 5 presents the final conclusion.