Estimating Reservoir Storage Variations by Combining Sentinel-2 and 3 Measurements in the Yliki Reservoir, Greece
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
In Situ Observations
2.2. Remote Sensing Data
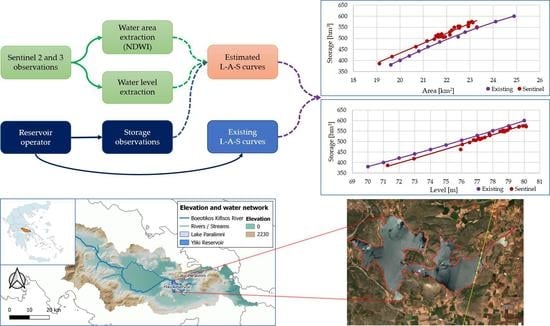
2.3. Methodology
2.3.1. Extracting Reservoir’s Water Area from Sentinel-2 Images
2.3.2. Extracting Reservoir’s Water Level from Sentinel-3 Measurements
2.3.3. Combination of Sentinel-2 and Sentinel-3 Measurements
2.3.4. Estimating Reservoir’s Storage Variation from Satellite Data
2.3.5. Comparing Remotely Sensed Reservoir Characteristics with a Known L–A–S Relationship
3. Results
3.1. Sentinel-2 Time Series
3.1.1. Sentinel-2-Derived Water Area—Storage Relationship and Reservoir Water Cycle
3.2. Sentinel-3 Time Series
3.2.1. Sentinel-3-Derived Water Level–Storage Relationship and Reservoir Water Cycle
3.3. Combination of Sentinel-2 and Sentinel-3 Data
3.4. Estimating Water Storage Variation
3.5. Comparison with Existing L–A–S Curve
4. Discussion
5. Conclusions
- Between March 2016 and September 2021, maximum and minimum water area observed were 23.14 km2 and 18.21 km2, respectively.
- Between November 2018 and September 2021, maximum and minimum water level observed were 80.1 m and 71.3 m, respectively.
- Water area short-term (monthly) maximum increase and decrease rates were calculated at 0.091 km2/d and 0.022 km2/d, respectively.
- Water level short-term (monthly) maximum increase and decrease rates were calculated at 0.132 m/d and 0.087 m/d, respectively.
- The estimation of storage variation for the available data range, corresponding to 64–96% of the reservoir capacity, was successful. The RMSE was found to be 7.69 hm3 (1.28% of reservoir capacity), and the correlation coefficient was 96.14%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Williamson, C.E.; Saros, J.E.; Vincent, W.F.; Smol, J.P. Lakes and Reservoirs as Sentinels, Integrators, and Regulators of Climate Change. Limnol. Oceanogr. 2009, 54, 2273–2282. [Google Scholar] [CrossRef]
- Busker, T.; de Roo, A.; Gelati, E.; Schwatke, C.; Adamovic, M.; Bisselink, B.; Pekel, J.-F.; Cottam, A. A Global Lake and Reservoir Volume Analysis Using a Surface Water Dataset and Satellite Altimetry. Hydrol. Earth Syst. Sci. Discuss. 2019, 23, 669–690. [Google Scholar] [CrossRef] [Green Version]
- Frappart, F.; Zeiger, P.; Betbeder, J.; Gond, V.; Bellot, R.; Baghdadi, N.; Blarel, F.; Darrozes, J.; Bourrel, L.; Seyler, F. Automatic Detec-Tion of Inland Water Bodies along Altimetry Tracks for Estimating Surface Water Storage Variations in the Congo Basin. Remote Sens. 2021, 10, 3804. [Google Scholar] [CrossRef]
- Kostianoy, A.G.; Lebedev, S.A.; Kostianaia, E.A.; Prokofiev, Y.A. Interannual Variability of Water Level in Two Largest Lakes of Europe. Remote Sens. 2022, 14, 659. [Google Scholar] [CrossRef]
- Gourgouletis, N.; Bariamis, G.; Baltas, E. Estimation of Characteristics of Surface Water Bodies Based on Sentinel-2 Images: The Case Study of Yliki Reservoir. In Proceedings of the Eighth International Conference on Environmental Management, Engineering, Planning & Economics, Thessaloniki, Greece, 20–24 July 2021; pp. 551–558. [Google Scholar]
- Schmitz, O.J.; Raymond, P.A.; Estes, J.A.; Kurz, W.A.; Holtgrieve, G.W.; Ritchie, M.E.; Schindler, D.E.; Spivak, A.C.; Wilson, R.W.; Bradford, M.A.; et al. Animating the Carbon Cycle. Ecosystems 2014, 17, 344–359. [Google Scholar] [CrossRef] [Green Version]
- Jimenez Cisneros, B.E.; Oki, T.; Arnell, N.W.; Benito, G.; Cogley, J.G.; Döll, P.; Jiang, T.; Mwakalila, S.S. Freshwater Resources. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V.R., Dokken, D.J., Mach, K.J., Mastrandrea, M.D., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 1199–1265. [Google Scholar]
- Kovats, R.S.; Valentini, R.M.; Bouwer, L.; Georgopoulou, E.; Jacob, D.; Martin, E.; Rounsevell, M.; Soussana, J.-F. Europe. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V.R., Dokken, D.J., Mach, K.J., Mastrandrea, M.D., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 1267–1326. [Google Scholar]
- Weatherhead, E.K.; Howden, N.J.K. The Relationship between Land Use and Surface Water Resources in the UK. Land Use Policy 2009, 26, S243–S250. [Google Scholar] [CrossRef]
- Thornton, P.K.; Herrero, M. The Inter-Linkages between Rapid Growth in Livestock Production, Climate Change, and the Impacts on Water Resources, Land Use, and Deforestation Background Paper to the 2010 World Development Report. 2010. Available online: http://hdl.handle.net/10986/9223 (accessed on 14 December 2021).
- Bariamis, G.; Paschos, G.; Baltas, E. Land Accounts in the River Basin Districts of Greece. Environ. Process. 2018, 5, 213–237. [Google Scholar] [CrossRef]
- Water and Climate Change Adaptation; OECD Studies on Water; OECD: Paris, France, 2013; ISBN 9789264200432.
- Karavitis, C.A.; Chortaria, C.; Alexandris, S.; Vasilakou, C.G.; Tsesmelis, D.E. Development of the Standardised Precipitation Index for Greece. Urban Water J. 2012, 9, 401–417. [Google Scholar] [CrossRef]
- Livada, I.; Assimakopoulos, V.D. Spatial and Temporal Analysis of Drought in Greece Using the Standardized Precipitation Index (SPI). Theor. Appl. Climatol. 2007, 89, 143–153. [Google Scholar] [CrossRef]
- Terzidis, G. Water Scarcity; Causes, Forecasting Potential and Mitigation Measures in the Urban and Agricultural Development of Greece. In Proceedings of the Water Scarcity and Floods, Geotechnical Chamber of Greece, Thessaloniki, Greece, 17 March 1992; pp. 25–40. [Google Scholar]
- Biswas, A.K. Integrated Water Resources Management: A Reassessment. Water Int. 2004, 29, 248–256. [Google Scholar] [CrossRef]
- Schwatke, C.; Dettmering, D.; Bosch, W.; Seitz, F. DAHITI—An Innovative Approach for Estimating Water Level Time Series over Inland Waters Using Multi-Mission Satellite Altimetry. Hydrol. Earth Syst. Sci. 2015, 19, 4345–4364. [Google Scholar] [CrossRef] [Green Version]
- Baup, F.; Frappart, F.; Maubant, J. Combining High-Resolution Satellite Images and Altimetry to Estimate the Volume of Small Lakes. Hydrol. Earth Syst. Sci. 2014, 18, 2007–2020. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Lv, A.; Zhu, W.; Yao, G.; Qi, S. Using Multisource Satellite Data to Investigate Lake Area, Water Level, and Water Storage Changes of Terminal Lakes in Ungauged Regions. Remote Sens. 2021, 13, 3221. [Google Scholar] [CrossRef]
- Lin, Y.; Li, X.; Zhang, T.; Chao, N.; Yu, J.; Cai, J.; Sneeuw, N. Water Volume Variations Estimation and Analysis Using Multisource Satellite Data: A Case Study of Lake Victoria. Remote Sens. 2020, 12, 3052. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, Y.; Ling, F.; Wang, Q.; Li, W.; Li, X. Water Bodies’ Mapping from Sentinel-2 Imagery with Modified Normalized Difference Water Index at 10-m Spatial Resolution Produced by Sharpening the Swir Band. Remote Sens. 2016, 8, 354. [Google Scholar] [CrossRef] [Green Version]
- Schmitt, M. Potential of Large-Scale Inland Water Body Mapping from Sentinel-1/2 Data on the Example of Bavaria’s Lakes and Rivers. PFG—J. Photogramm. Remote Sens. Geoinf. Sci. 2020, 88, 271–289. [Google Scholar] [CrossRef]
- Carabajal, C.C.; Boy, J.P. Lake and Reservoir Volume Variations in South America from Radar Altimetry, ICESat Laser Altimetry, and GRACE Time-Variable Gravity. Adv. Space Res. 2021, 68, 652–671. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. Estimating Water Volume Variations in Lakes and Reservoirs from Four Operational Satellite Altimetry Databases and Satellite Imagery Data. Remote Sens. Environ. 2013, 134, 403–416. [Google Scholar] [CrossRef]
- Song, C.; Huang, B.; Ke, L. Inter-Annual Changes of Alpine Inland Lake Water Storage on the Tibetan Plateau: Detection and Analysis by Integrating Satellite Altimetry and Optical Imagery. Hydrol. Processes 2014, 28, 2411–2418. [Google Scholar] [CrossRef]
- Kittel, C.M.M.; Jiang, L.; Tøttrup, C.; Bauer-Gottwein, P. Sentinel-3 Radar Altimetry for River Monitoring—A Catchment-Scale Evaluation of Satellite Water Surface Elevation from Sentinel-3A and Sentinel-3B. Hydrol. Earth Syst. Sci. 2021, 25, 333–357. [Google Scholar] [CrossRef]
- Arsen, A.; Crétaux, J.F.; Berge-Nguyen, M.; del Rio, R.A. Remote Sensing-Derived Bathymetry of Lake Poopó. Remote Sens. 2013, 6, 407–420. [Google Scholar] [CrossRef] [Green Version]
- Elsahabi, M.; Makboul, O.; Negm, A.M. Lake Nubia Bathymetry Detection by Satellite Remote Sensing. Int. Water Technol. J. IWTJ 2018, 8, 9–17. [Google Scholar]
- Forfinski-Sarkozi, N.A.; Parrish, C.E. Analysis of MABEL Bathymetry in Keweenaw Bay and Implications for ICESat-2 ATLAS. Remote Sens. 2016, 8, 772. [Google Scholar] [CrossRef] [Green Version]
- Getirana, A.; Jung, H.C.; Tseng, K.H. Deriving Three Dimensional Reservoir Bathymetry from Multi-Satellite Datasets. Remote Sens. Environ. 2018, 217, 366–374. [Google Scholar] [CrossRef]
- Markogianni, V.; Kalivas, D.; Petropoulos, G.P.; Dimitriou, E. Modelling of Greek Lakes Water Quality Using Earth Observation in the Framework of the Water Framework Directive (WFD). Remote Sens. 2022, 14, 739. [Google Scholar] [CrossRef]
- Peppa, M.; Vasilakos, C.; Kavroudakis, D. Eutrophication Monitoring for Lake Pamvotis, Greece, Using Sentinel-2 Data. ISPRS Int. J. Geo-Inf. 2020, 9, 143. [Google Scholar] [CrossRef] [Green Version]
- Alexandridis, T.K.; Takavakoglou, V.; Crisman, T.L.; Zalidis, G.C. Remote Sensing and GIS Techniques for Selecting a Sustainable Scenario for Lake Koronia, Greece. Environ. Manag. 2007, 39, 278–290. [Google Scholar] [CrossRef]
- Papastergiadou, E.S.; Retalis, A.; Apostolakis, A.; Georgiadis, T. Environmental Monitoring of Spatio-Temporal Changes Using Remote Sensing and GIS in a Mediterranean Wetland of Northern Greece. Water Resour. Manag. 2008, 22, 579–594. [Google Scholar] [CrossRef]
- Psomiadis, E.; Soulis, K.X.; Zoka, M.; Dercas, N. Synergistic Approach of Remote Sensing and Gis Techniques for Flash-Flood Monitoring and Damage Assessment in Thessaly Plain Area, Greece. Water 2019, 11, 448. [Google Scholar] [CrossRef] [Green Version]
- Capolongo, D.; Refice, A.; Bocchiola, D.; D’Addabbo, A.; Vouvalidis, K.; Soncini, A.; Zingaro, M.; Bovenga, F.; Stamatopoulos, L. Coupling Multitemporal Remote Sensing with Geomorphology and Hydrological Modeling for Post Flood Recovery in the Strymonas Dammed River Basin (Greece). Sci. Total Environ. 2019, 651, 1958–1968. [Google Scholar] [CrossRef]
- Kontopoulou, E.; Kolokoussis, P.; Karantzalos, K. Water Quality Estimation in Greek Lakes from Landsat 8 Multispectral Satellite Data. Eur. Water 2017, 58, 191–196. [Google Scholar]
- Elhag, M.; Yilmaz, N. Insights of Remote Sensing Data to Surmount Rainfall/Runoff Data Limitations of the Downstream Catchment of Pineios River, Greece. Environ. Earth Sci. 2021, 80, 35. [Google Scholar] [CrossRef]
- Special Secreteriat for Water. 1st Revision of the Management Plan of the River Basin District of Eastern Central Greece. Athens. 2017. Available online: http://wfdver.ypeka.gr/el/management-plans-gr/1revision-approved-management-plans-gr/approved-1revision-el07-gr/ (accessed on 6 January 2022).
- EYDAP. Water Supply Resources. Available online: https://www.eydap.gr/en/TheCompany/Water/WaterSources/ (accessed on 6 January 2022).
- Special Secreteriat for Water. Strategic Environmental Impact Assessment of the 1st Revision of the River Basin District Management Plan of Eastern Central Greece (EL07). Athens. 2017. Available online: http://wfdver.ypeka.gr/el/project/consultation-el07-18-1revision-smpe-gr/ (accessed on 6 January 2022).
- Efstratiadis, A.; Tsoukalas, I. Revision of the Yliki and Paralimni Water Balance and Evaluation of the Overflow Risk during Current Hydrologic Year. Athens. 2019. Available online: http://www.itia.ntua.gr/el/docinfo/2014/ (accessed on 14 December 2021).
- EYDAP. Raw Water Reserves. Available online: https://www.eydap.gr/en/TheCompany/Water/Savings/ (accessed on 14 December 2021).
- SUHET. SENTINEL-2 User Handbook. 2015. Available online: https://sentinels.copernicus.eu/web/sentinel/user-guides/document-library/-/asset_publisher/xlslt4309D5h/content/sentinel-2-user-handbook (accessed on 21 October 2021).
- European Space Agency. Sentinel-3 Altimetry Technical Guide. Available online: https://sentinel.esa.int/web/sentinel/technical-guides/sentinel-3-altimetry/ (accessed on 21 October 2021).
- European Space Agency. Sentinel-3 Atlimetry Overview. Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-3-altimetry/overview (accessed on 10 October 2021).
- EUMETSAT. Past Processing Baselines. Available online: https://www.eumetsat.int/past-processing-baselines (accessed on 23 October 2021).
- European Space Agency; French Space Agency. Radar Altimetry Tutorial & Toolbox. Available online: http://www.altimetry.info/radar-altimetry-tutorial/data-flow/data-processing/retracking/ (accessed on 27 October 2021).
- Yang, X.; Zhao, S.; Qin, X.; Zhao, N.; Liang, L. Mapping of Urban Surface Water Bodies from Sentinel-2 MSI Imagery at 10 m Resolution via NDWI-Based Image Sharpening. Remote Sens. 2017, 9, 596. [Google Scholar] [CrossRef] [Green Version]
- Cavallo, C.; Papa, M.N.; Gargiulo, M.; Palau-Salvador, G.; Vezza, P.; Ruello, G. Continuous Monitoring of the Flooding Dynamics in the Albufera Wetland (Spain) by Landsat-8 and Sentinel-2 Datasets. Remote Sens. 2021, 13, 3525. [Google Scholar] [CrossRef]
- McFeeters, S.K. The Use of the Normalized Difference Water Index (NDWI) in the Delineation of Open Water Features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Sekertekin, A. A Survey on Global Thresholding Methods for Mapping Open Water Body Using Sentinel-2 Satellite Imagery and Normalized Difference Water Index. Arch. Comput. Methods Eng. 2021, 28, 1335–1347. [Google Scholar] [CrossRef]
- Prewitt, J.M.S.; Mendelsohn, M.L. The Analysis of Cell Images. Ann. N. Y. Acad. Sci. 2006, 128, 1035–1053. [Google Scholar] [CrossRef]
- Crétaux, J.F.; Bergé-Nguyen, M.; Calmant, S.; Jamangulova, N.; Satylkanov, R.; Lyard, F.; Perosanz, F.; Verron, J.; Montazem, A.S.; Le Guilcher, G.; et al. Absolute Calibration or Validation of the Altimeters on the Sentinel-3A and the Jason-3 over Lake Issykkul (Kyrgyzstan). Remote Sens. 2018, 10, 1679. [Google Scholar] [CrossRef] [Green Version]
- Crétaux, J.F.; Abarca-del-Río, R.; Bergé-Nguyen, M.; Arsen, A.; Drolon, V.; Clos, G.; Maisongrande, P. Lake Volume Monitoring from Space. Surv. Geophys. 2016, 37, 269–305. [Google Scholar] [CrossRef] [Green Version]
- Vignudelli, S.; Scozzari, A.; Abileah, R.; Scozzari, A. A Completely Remote Sensing Approach To Monitoring Reservoirs Water Volume. Int. Water Technol. J. 2011, 1, 63–77. [Google Scholar]














Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gourgouletis, N.; Bariamis, G.; Anagnostou, M.N.; Baltas, E. Estimating Reservoir Storage Variations by Combining Sentinel-2 and 3 Measurements in the Yliki Reservoir, Greece. Remote Sens. 2022, 14, 1860. https://doi.org/10.3390/rs14081860
Gourgouletis N, Bariamis G, Anagnostou MN, Baltas E. Estimating Reservoir Storage Variations by Combining Sentinel-2 and 3 Measurements in the Yliki Reservoir, Greece. Remote Sensing. 2022; 14(8):1860. https://doi.org/10.3390/rs14081860
Chicago/Turabian StyleGourgouletis, Nikolaos, Georgios Bariamis, Marios N. Anagnostou, and Evangelos Baltas. 2022. "Estimating Reservoir Storage Variations by Combining Sentinel-2 and 3 Measurements in the Yliki Reservoir, Greece" Remote Sensing 14, no. 8: 1860. https://doi.org/10.3390/rs14081860
APA StyleGourgouletis, N., Bariamis, G., Anagnostou, M. N., & Baltas, E. (2022). Estimating Reservoir Storage Variations by Combining Sentinel-2 and 3 Measurements in the Yliki Reservoir, Greece. Remote Sensing, 14(8), 1860. https://doi.org/10.3390/rs14081860