A Scalable Method to Improve Large-Scale Lidar Topographic Differencing Results
Abstract
:1. Introduction
2. Indiana Statewide Multitemporal Lidar Datasets
3. Methodology
3.1. Extracting Additional Information
3.1.1. Water Mask
3.1.2. Flight Path Boundary Information
3.2. Estimating Erroneous Displacements of Target (2011–2013) DTMs
3.2.1. Gathering Height Values
3.2.2. Histogram-Based Comparison
3.3. Generating Improved Differencing Results
4. Experimental Results
4.1. Study Sites
4.2. Effectiveness of Proposed Method
4.2.1. Estimated Displacements by Vertical Positioning Errors
4.2.2. Improved County-Level DoD Results
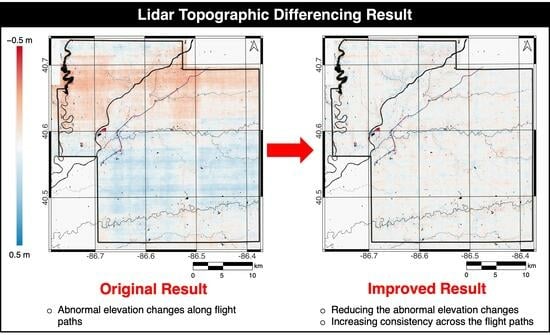
- Comparison on a county-level scale
- Detailed comparison with examples



4.3. Remaining Horizontal Positioning Errors
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wheaton, J.M.; Brasington, J.; Darby, S.E.; Sear, D.A. Accounting for uncertainty in DEMs from repeat topographic surveys: Improved sediment budgets. Earth Surf. Process. Landf. 2010, 35, 136–156. [Google Scholar] [CrossRef]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arıkan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514, 1–13. [Google Scholar] [CrossRef]
- Brozzetti, F.; Mondini, A.C.; Pauselli, C.; Mancinelli, P.; Cirillo, D.; Guzzetti, F.; Lavecchia, G. Mainshock anticipated by intra-sequence ground deformations: Insights from multiscale field and SAR interferometric measurements. Geosciences 2020, 10, 186. [Google Scholar] [CrossRef]
- Eltner, A.; Baumgart, P. Accuracy constraints of terrestrial Lidar data for soil erosion measurement: Application to a Mediterranean field plot. Geomorphology 2015, 245, 243–254. [Google Scholar] [CrossRef]
- Jones, L.; Hobbs, P. The application of terrestrial LiDAR for geohazard mapping, monitoring and modelling in the British Geological Survey. Remote Sens. 2021, 13, 395. [Google Scholar] [CrossRef]
- Joerg, P.C.; Morsdorf, F.; Zemp, M. Uncertainty assessment of multi-temporal airborne laser scanning data: A case study on an Alpine glacier. Remote Sens. Environ. 2012, 127, 118–129. [Google Scholar] [CrossRef]
- Oskin, M.E.; Arrowsmith, J.R.; Corona, A.H.; Elliott, A.J.; Fletcher, J.M.; Fielding, E.J.; Gold, P.O.; Garcia, J.J.G.; Hudnut, K.W.; Liu-Zeng, J.; et al. Near-field deformation from the El Mayor–Cucapah earthquake revealed by differential LIDAR. Science 2012, 335, 702–705. [Google Scholar] [CrossRef]
- Clark, K.J.; Nissen, E.K.; Howarth, J.D.; Hamling, I.J.; Mountjoy, J.J.; Ries, W.F.; Jones, K.; Goldstein, S.; Cochran, U.A.; Villamor, P.; et al. Highly variable coastal deformation in the 2016 Mw7. 8 Kaikōura earthquake reflects rupture complexity along a transpressional plate boundary. Earth Planet. Sci. Lett. 2017, 474, 334–344. [Google Scholar] [CrossRef]
- Ghuffar, S. DEM generation from multi satellite PlanetScope imagery. Remote Sens. 2018, 10, 1462. [Google Scholar] [CrossRef]
- Virtanen, J.P.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Turppa, T.; Hyyppä, H.; Hyyppä, J. Nationwide point cloud—The future topographic core data. ISPRS Int. J. GeoInf. 2017, 6, 243. [Google Scholar] [CrossRef]
- Li, X.; Liu, C.; Wang, Z.; Xie, X.; Li, D.; Xu, L. Airborne LiDAR: State-of-the-art of system design, technology and application. Meas. Sci. Technol. 2021, 32, 032002. [Google Scholar] [CrossRef]
- Chen, R.F.; Chang, K.J.; Angelier, J.; Chan, Y.C.; Deffontaines, B.; Lee, C.T.; Lin, M.L. Topographical changes revealed by high-resolution airborne LiDAR data: The 1999 Tsaoling landslide induced by the Chi–Chi earthquake. Eng. Geol. 2006, 88, 160–172. [Google Scholar] [CrossRef]
- Favalli, M.; Fornaciai, A.; Mazzarini, F.; Harris, A.; Neri, M.; Behncke, B.; Pareschi, M.T.; Tarquini, S.; Boschi, E. Evolution of an active lava flow field using a multitemporal LIDAR acquisition. J. Geophys. Res. 2010, 115, B11203. [Google Scholar] [CrossRef]
- Glennie, C.; Hinojosa-Corona, A.; Nissen, E.; Kusari, A.; Oskin, M.; Arrowsmith, J.; Borsa, A. Optimization of legacy lidar data sets for measuring near-field earthquake displacement. Geophys. Res. Lett. 2014, 41, 3494–3501. [Google Scholar] [CrossRef]
- Wagner, W.; Lague, D.; Mohrig, D.; Passalacqua, P.; Shaw, J.; Moffett, K. Elevation change and stability on a prograding delta. Geophys. Res. Lett. 2017, 44, 1786–1794. [Google Scholar] [CrossRef]
- DeLong, S.B.; Hammer, M.N.; Engle, Z.T.; Richard, E.M.; Breckenridge, A.J.; Gran, K.B.; Jennings, C.E.; Jalobeanu, A. Regional-scale landscape response to an extreme precipitation event from repeat lidar and object-based image analysis. Earth Space Sci. 2022, 9, e2022EA002420. [Google Scholar] [CrossRef]
- Entwistle, N.; Heritage, G.; Milan, D. Recent remote sensing applications for hydro and morphodynamic monitoring and modelling. Earth Surf. Process. Landf. 2018, 43, 2283–2291. [Google Scholar] [CrossRef]
- Okyay, U.; Telling, J.; Glennie, C.L.; Dietrich, W.E. Airborne lidar change detection: An overview of Earth sciences applications. Earth Sci. Rev. 2019, 198, 102929. [Google Scholar] [CrossRef]
- Zhong, C.; Liu, Y.; Gao, P.; Chen, W.; Li, H.; Hou, Y.; Nuremanguli, T.; Ma, H. Landslide mapping with remote sensing: Challenges and opportunities. Int. J. Remote Sens. 2020, 41, 1555–1581. [Google Scholar] [CrossRef]
- Chen, Z.; Gao, B.; Devereux, B. State-of-the-art: DTM generation using airborne lidar data. Sensors 2017, 17, 150. [Google Scholar] [CrossRef]
- Mitasova, H.; Drake, T.G.; Bernstein, D.; Harmon, R.S. Quantifying rapid changes in coastal topography using modern mapping techniques and geographic information system. Environ. Eng. Geosci. 2004, 10, 1–11. [Google Scholar] [CrossRef]
- Anderson, S.; Pitlick, J. Using repeat lidar to estimate sediment transport in a steep stream. J. Geophys. Res. Earth Surf. 2014, 119, 621–643. [Google Scholar] [CrossRef]
- Mora, O.E.; Lenzano, M.G.; Toth, C.K.; Grejner-Brzezinska, D.A.; Fayne, J.V. Landslide change detection based on multi-temporal Airborne LiDAR-derived DEMs. Geosciences 2018, 8, 23. [Google Scholar] [CrossRef]
- Scott, C.P.; Beckley, M.; Phan, M.; Zawacki, E.; Crosby, C.; Nandigam, V.; Arrowsmith, R. Statewide USGS 3DEP lidar topographic differencing applied to Indiana, USA. Remote Sens. 2022, 14, 847. [Google Scholar] [CrossRef]
- Favalli, M.; Fornaciai, A.; Pareschi, M.T. LIDAR strip adjustment: Application to volcanic areas. Geomorphology 2009, 111, 123–135. [Google Scholar] [CrossRef]
- What Is 3DEP? Available online: https://www.usgs.gov/3d-elevation-program/what-3dep (accessed on 15 July 2022).
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor Fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 12–15 November 1991. [Google Scholar] [CrossRef]
- Lallias-Tacon, S.; Liébault, F.; Piégay, H. Step by step error assessment in braided river sediment budget using airborne LiDAR data. Geomorphology 2014, 214, 307–323. [Google Scholar] [CrossRef]
- Nilsson, M.; Nordkvist, K.; Jonzén, J.; Lindgren, N.; Axensten, P.; Wallerman, J.; Egberth, M.; Larsson, S.; Nilsson, L.; Eriksson, J.; et al. A nationwide forest attribute map of Sweden predicted using airborne laser scanning data and field data from the National Forest Inventory. Remote Sens. Environ. 2017, 194, 447–454. [Google Scholar] [CrossRef]
- Stoker, J.; Miller, B. The accuracy and consistency of 3d elevation program data: A systematic analysis. Remote Sens. 2022, 14, 940. [Google Scholar] [CrossRef]
- Cserép, M.; Lindenbergh, R. Distributed processing of Dutch AHN laser altimetry changes of the built-up area. Int. J. Appl. Earth Obs. Geoinf. 2023, 116, 103174. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y. A fast global interpolation method for digital terrain model generation from large LiDAR-derived data. Remote Sens. 2019, 11, 1324. [Google Scholar] [CrossRef]
- Aljumaily, H.; Laefer, D.F.; Cuadra, D.; Velasco, M. Voxel change: Big data–based change detection for aerial urban LiDAR of unequal densities. J. Surv. Eng. 2021, 147, 04021023. [Google Scholar] [CrossRef]
- Oh, S.; Jung, J.; Shao, G.; Shao, G.; Gallion, J.; Fei, S. High-resolution canopy height model generation and validation using USGS 3DEP lidar data in Indiana, UAS. Remote Sens. 2022, 14, 935. [Google Scholar] [CrossRef]
- Indiana’s New 3DEP LiDAR Data and Informational Resources. Available online: https://igic.memberclicks.net/indiana-s-new-3dep-lidar-data-and-informational-resources (accessed on 31 July 2022).
- LiDAR Data Hosted by iDiF @ Purdue. Available online: https://lidar.digitalforestry.org (accessed on 15 July 2022).
- Topographic Data Quality Levels (QLs). Available online: https://www.usgs.gov/3d-elevation-program/topographic-data-quality-levels-qls (accessed on 10 October 2022).
- Indiana Statewide Topographic Differencing. Available online: https://portal.opentopography.org/indiana (accessed on 15 July 2022).
- Habib, A.; Kersting, A.P.; Bang, K.I.; Lee, D.C. Alternative methodologies for the internal quality control of parallel LiDAR strips. IEEE Trans. Geosci. Remote Sens. 2009, 48, 221–236. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Moore, R.B.; McKay, L.D.; Rea, A.H.; Bondelid, T.R.; Price, C.V.; Dewald, T.G.; Johnston, C.M. User’s Guide for the National Hydrography Dataset Plus (NHDPlus) High Resolution; U.S. Geological Survey Open-File Report 2019-1096; U.S. Geological Survey: Reston, VA, USA, 2019; p. 66. [Google Scholar] [CrossRef]
- TNM Download (v2.0). Available online: https://apps.nationalmap.gov/downloader/ (accessed on 4 February 2023).
- Florinsky, I.V. Errors of signal processing in digital terrain modelling. Int. J. Geogr. Inf. Sci. 2002, 16, 475–501. [Google Scholar] [CrossRef]
- Hyyppä, H.; Yu, X.; Hyyppä, J.; Kaartinen, H.; Kaasalainen, S.; Honkavaara, E.; Rönnholm, P. Factors affecting the quality of DTM generation in forested areas. In Proceedings of the ISPRS WG III/3, III/4, V/3 Workshop Laser Scanning 2005, Enschede, The Netherlands, 12–14 September 2005. [Google Scholar]
- Wilson, J.P.; Gallant, J.C. Terrain Analysis: Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2000; pp. 15–20. [Google Scholar]
- Lv, Z.Y.; Liu, T.F.; Zhang, P.; Benediktsson, J.A.; Lei, T.; Zhang, X. Novel adaptive histogram trend similarity approach for land cover change detection by using bitemporal very-high-resolution remote sensing images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9554–9574. [Google Scholar] [CrossRef]
- Chen, H.M.; Arora, M.K.; Varshney, P.K. Mutual information-based image registration for remote sensing data. Int. J. Remote Sens. 2003, 24, 3701–3706. [Google Scholar] [CrossRef]
- Shen, D. Image registration by local histogram matching. Pattern Recognit. 2007, 40, 1161–1172. [Google Scholar] [CrossRef]
- Cha, S.H. Taxonomy of nominal type histogram distance measures. In Proceedings of the American Conference on Applied Mathematics, Havard, MA, USA, 24–26 March 2008; pp. 325–330. [Google Scholar]
- Swain, M.J.; Ballard, D.H. Color indexing. Int. J. Comput. Vis. 1991, 7, 11–32. [Google Scholar] [CrossRef]
- Nummiaro, K.; Koller-Meier, E.; Van Gool, L. An adaptive color-based particle filter. Image Vis. Comput. 2003, 21, 99–110. [Google Scholar] [CrossRef]
- Pele, O.; Werman, M. The quadratic-chi histogram distance family. In Proceedings of the 11th European Conference on Computer Vision, Heraklion, Crete, Greece, 5–11 September 2010; Daniilidis, K., Maragos, P., Paragios, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 749–762. [Google Scholar] [CrossRef]
- Goodman, L.A. Kolmogorov-Smirnov tests for psychological research. Psychol. Bull. 1954, 51, 160–168. [Google Scholar] [CrossRef] [PubMed]
- Williams, R. DEMs of difference. Geomorphol. Tech. 2012, 2, 1–17. [Google Scholar]
- NASA JPL. NASA Shuttle Radar Topography Mission Water Body Data Shapefiles & Raster Files. Distributed by NASA EOSDIS Land Processes Distributed Active Archive Center; NASA: Washington, DC, USA, 2013. [Google Scholar] [CrossRef]
- Global Surface Water—Data Access. Available online: https://global-surface-water.appspot.com/download (accessed on 11 August 2023).










| County | The Number of Tiles | Area (km2) | The Number of Flight Path Pairs | Acquisition Months | |
|---|---|---|---|---|---|
| 2011–2013 | 2016–2020 | ||||
| Boone | 520 | 808.1 | 1057 | 2011/03, 2011/04, 2011/09 | 2018/03, 2018/04 |
| Brown | 414 | 1147.1 | 183 | 2011/03 | 2017/03, 2017/04, 2018/03 |
| Carroll | 450 | 964.0 | 799 | 2011/03, 2011/04 | 2018/03, 2018/04 |
| Decatur | 469 | 965.0 | 956 | 2012/03, 2012/04, 2012/12 | 2017/03, 2017/04, 2018/03 |
| Kosciusko | 651 | 1376.3 | 342 | 2011/03, 2011/04, 2012/03 | 2017/03, 2017/04 |
| Monroe | 525 | 1021.8 | 2241 | 2011/03, 2011/09 | 2017/04, 2018/03, 2018/04, 2018/12, 2019/03 |
| Starke | 399 | 800.6 | 316 | 2011/03, 2011/04 | 2018/03, 2018/04 |
| Tippecanoe | 648 | 1294.5 | 284 | 2013/03, 2013/04 | 2018/03, 2018/04 |
| Total | 4076 | 8377.4 | 6178 | - | - |
| County | Boone | Brown | Carroll | Decatur |
| 5th | −0.131 | −0.345 | −0.101 | −0.131 |
| 95th | 0.006 | 0.052 | 0.143 | 0.021 |
| County | Kosciusko | Monroe | Starke | Tippecanoe |
| 5th | −0.070 | −0.162 | −0.040 | −0.147 |
| 95th | 0.143 | 0.006 | 0.147 | 0.021 |
| County | Boone | Brown | Carroll | Decatur | |||||
| DoD | Original | Adjusted | Original | Adjusted | Original | Adjusted | Original | Adjusted | |
| Mean | m | 0.0629 | 0.0025 | 0.1701 | 0.0200 | 0.0546 | 0.0023 | 0.0562 | 0.0026 |
| R | % | - | 96.0 | - | 88.3 | - | 95.9 | - | 95.5 |
| STD | m | 0.0336 | 0.0030 | 0.1462 | 0.0240 | 0.0680 | 0.0031 | 0.0424 | 0.0037 |
| County | Kosciusko | Monroe | Starke | Tippecanoe | |||||
| DoD | Original | Adjusted | Original | Adjusted | Original | Adjusted | Original | Adjusted | |
| Mean | m | 0.0441 | 0.0195 | 0.0740 | 0.0210 | 0.0624 | 0.0084 | 0.0175 | 0.0065 |
| R | % | - | 55.7 | - | 71.6 | - | 86.5 | - | 62.8 |
| STD | m | 0.0618 | 0.0223 | 0.0545 | 0.0343 | 0.0499 | 0.0117 | 0.0170 | 0.0108 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, M.; Jung, J. A Scalable Method to Improve Large-Scale Lidar Topographic Differencing Results. Remote Sens. 2023, 15, 4289. https://doi.org/10.3390/rs15174289
Jung M, Jung J. A Scalable Method to Improve Large-Scale Lidar Topographic Differencing Results. Remote Sensing. 2023; 15(17):4289. https://doi.org/10.3390/rs15174289
Chicago/Turabian StyleJung, Minyoung, and Jinha Jung. 2023. "A Scalable Method to Improve Large-Scale Lidar Topographic Differencing Results" Remote Sensing 15, no. 17: 4289. https://doi.org/10.3390/rs15174289
APA StyleJung, M., & Jung, J. (2023). A Scalable Method to Improve Large-Scale Lidar Topographic Differencing Results. Remote Sensing, 15(17), 4289. https://doi.org/10.3390/rs15174289