1. Introduction
Remote sensing, with its advantages of wide observation ranges, short time cycles, and dynamic tracking, has become the primary means of Earth observation. Hyperspectral remote sensing technology, as an organic combination of spectral and imaging techniques, uses imaging spectrometers to measure radiation intensity within a wide spectral range for specific scenes, generating a data cube that combines one-dimensional spectral responses with two-dimensional spatial information. This enables the synchronous acquisition of geometric, radiometric, and spectral information pertaining to target objects. Compared to traditional remote sensing, hyperspectral remote sensing provides more abundant spectral–spatial information, greatly promoting the transition from qualitative analysis to quantitative analysis in remote sensing [
1]. The spectral fusion characteristic of hyperspectral image (HSI) data gives it prominent advantages in the fine classification and identification of land cover, making it widely applied in fields such as geological survey [
2], precision agriculture [
3], forest inventory [
4], environmental monitoring [
5], biomedical research [
6], and more.
HSI data has the advantage of high spectral resolution, allowing it to capture delicate spectral characteristics of the interested target. This has made land cover classification a popular research direction in the field of HSI analysis [
7]. Considering the high-dimensional nature of HSI samples, researchers have applied various machine learning methods to HSI classification over the past few decades, including logistic regression [
8], Support Vector Machines (SVM) [
9], Sparse Representation [
10], Random Forest (RF) [
11], and Decision Trees [
12]. However, due to the limited number of available training samples regarding HSI data, which often cannot satisfy the requirements of the spectral dimension, these classifiers still exhibit inadequate classification performance on the original data [
13]. Additionally, the high-spectral-resolution HSI data inevitably contain a certain amount of redundant information between adjacent spectral bands [
14], and the original spectral features are often not the most effective representation for distinguishing the target of interest.
To address the aforementioned problems, HSI feature extraction methods have emerged. The purpose of these methods is to explore discriminative information of different objects in order to enable more accurate category prediction in the feature space via the use of classifiers. Early feature extraction methods include singular spectrum analysis (SSA) [
15], principal component analysis (PCA) [
16], linear discriminant analysis (LDA) [
17], and independent component analysis (ICA) [
18], which primarily extract features by learning linear combinations of independent pixels. However, these methods often lack the consideration of spatial contextual information, leading to issues such as outliers and pixel-level misclassification in the resulting classification maps, seriously affecting the reliability of the results. As a result, more research studies have focused on how to extract effective spatial information and integrate it with spectral information for classification tasks [
19]. Ref. [
20] leverages the advantages of edge-preserving filters (EPF) in extracting image spatial structures by adjusting the parameters of the filters to obtain hyperspectral image spatial information at different scales. In [
21], HSI data were treated as a complete tensor, and a three-dimensional discrete wavelet transform was designed to decompose the data into geometric and statistical spatial structures.
The deep learning techniques in HSI classification have received widespread attention in recent years. Researchers have proposed deep learning-based multiscale spatial–spectral classification methods. Compared to traditional methods, deep neural networks have the advantage of extracting high-level nonlinear features from images [
22]. In a study by Liang et al., the VGG16 network was used to extract spatial information at different levels of HSI as spatial features at different scales [
23]. Wang et. al designed multiscale feature extraction sub-networks for the spectral and spatial information of HSI data. They proposed an adaptive spectral and spatial feature combination method, achieving the collaborative classification of spectral information [
24]. A model combining a Convolutional Neural Network (CNN) and Recurrent Neural Network (RNN) was proposed to enhance the discriminative ability of spectral features in [
25]. A deep 1D CNN model, which takes pixel vectors as input data and performs classification on hyperspectral data only in the spectral dimension, achieved outstanding accuracy surpassing traditional SVM classifiers [
26]. Wan et al. introduced a Graph Convolutional Network (GCN) to overcome the issue of traditional CNN models’ inability to adapt to the distribution and geometric shapes of different objects. They constructed multiple input graphs with different neighborhood scales to achieve multiscale classification [
27].
The Vision Transformer (ViT) [
28] is the first transformer network for the visual domain. The network treats image patches as inputs and maps them into features that are integrated into the ViT model. Following the emergence of ViTs, many studies have aimed to incorporate transformers such as IPT [
29], PVT [
30], and the Swin Transformer [
31] into image processing. Wang et al. combined K-nearest neighbor attention to utilize the local features of image patches and suppressed redundant information by only considering a subset of attention weights with the highest similarity [
32]. Mou et al. designed a spectral attention module that applies different attention weights to guide the network to focus on discriminative spectral information through a gating mechanism [
33]. Refiner explored the potential of attention expansion in high-dimensional space and enhanced the local structural characteristics of attention maps using convolutional operations [
34]. Zhu et al. studied the attention mechanism in spectral and spatial information and proposed the Residual Spectral–Spatial Attention (RSSAN) mechanism [
35], which selectively captures useful features in the spectral and spatial dimensions to improve hyperspectral classification. He et al. introduced a bidirectional encoder representation from a transformer (BERT) model [
36], and a new feature channel-based attention calculation method which improves the processing efficiency of high-resolution images compared to existing token-based attention calculation methods was also proposed [
37]. Hong et al. proposed SpectralFormer [
38], which captures local spectral sequence knowledge from neighboring spectral bands through pixel- or patch-wise inputs. Zhong et al. introduced a spectral-spatial transformer network, which includes a spatial attention module and a spectral correlation module [
39]. Some new transformer-based architectures [
40,
41,
42,
43,
44,
45,
46] were employed in HSI classification fields and achieved good performance.
In all supervised learning algorithms, the ultimate goal is to train a model that performs well in all aspects and remains stable. However, achieving such ideal results is often challenging. In many cases, only multiple models that excel in certain aspects can be trained (known as weakly supervised models). Ensemble learning aims to combine these weakly supervised models to create a more robust and accurate strongly supervised model. The fundamental idea behind ensemble learning is that by fusing predictions from diverse weak classifiers, errors made by one classifier can be corrected by others, ultimately improving overall performance. Typically, we test new data using a well-converged network to achieve good prediction results. However, in the case of HSI classification, when training samples are limited, a single classification network may perform poorly. Continuously improving the model structure and introducing more feature extraction modules can enhance the network’s feature extraction ability, which can theoretically continuously improve classification accuracy. However, this approach requires more data and greater algorithm requirements, meaning that it is more costly. The advantage of ensemble learning lies in its fewer requirements for each participating algorithm. By designing different ensemble strategies, it often achieves unexpectedly good classification accuracy, so it has a wide range of practical applications. Therefore, this paper adopts an ensemble learning approach using a two-level ensemble strategy to combine the outcomes of several single-classification networks based on ViT. Due to their different architectural designs, each ViT model has different feature extraction capabilities and can extract features for classification from multiple different aspects, which ensures that each basic ViT classifier has a large degree of diversity. Hence, the proposed approach yields stable and high-performing classification maps for HSI classification.
The main contributions of this paper are as follows:
Proposed an ensemble learning framework based on ViT that combines the classification performance of multiple ViT models using two levels of ensemble strategies. The two ensemble strategies consistently achieve higher classification accuracy compared to individual ViT methods.
Introduced the spatial shuffle pre-processing technique, which converts the three-dimensional cubic data into two-dimensional images for processing, making it more suitable for the ViT architecture.
With the two-level ensemble strategies, there is no need to divide a validation set to maximize the utilization of all precious and limited training data. Instead, the models from each training epoch can be directly used for predictions on the test data. The predictions are then ensemble, eliminating the impact of model fitting parameters and achieving more stable and higher classification accuracy.
The following sections of this manuscript are structured as follows. Seven ViT-based methods are described in
Section 2, as well as the spatial shuffle preprocessing operation and the ensemble strategy used in this study.
Section 3 and
Section 4 present the comparative experiments and the corresponding discussions, respectively.
Section 5 presents the concluding remarks of the study.
2. Proposed Method
2.1. ViT [28]
ViT is a model that utilizes the transformer architecture for image classification purposes. Its simplicity, excellent performance, and scalability have made ViT a significant milestone for the application of transformers in computer vision. While transformers have been widely used in natural language processing tasks, their application in computer vision still has certain limitations. Presently, in the domain of computer vision, attention mechanisms are either integrated with CNNs or employed to substitute specific components of CNNs while keeping the overall structure intact. However, ViT challenges this conventional reliance on CNNs by demonstrating that using pure transformers on sequences of image patches can effectively perform image classification tasks. Through the authors’ experiments, ViT has shown outstanding results while consuming fewer computational resources.
ViT divides the input image into 16 × 16 patches and converts them into fixed-length vectors. These vectors are then processed by a transformer for further computations. The subsequent encoder operations maintain the same principles as the original transformer model. However, for image classification purposes, a special token is included in the input sequence. The output corresponding to this token determines the predicted class of the image. The basic process is as follows: First, the input image is divided into patches, with each patch having a size of 16 × 16. Then, each patch is passed through an embedding layer known as the Linear Projection of Flattened Patches, which produces a series of vectors (tokens), with each patch corresponding to one vector. Additionally, a special token for classification is added before all the vectors, with the same dimension as the other vectors. Positional information is also incorporated. Next, all tokens are input into the transformer encoder, and the encoder is stacked L times. The output of the special token for classification is then fed into an MLP Head, resulting in the final classification result.
2.2. SimpleViT [47]
The main differences from ViT are as follows: the batch size is 1024 instead of 4096, it uses global average or max pooling without a class token, it incorporates fixed sin–cos positional embeddings, and it applies data augmentation techniques such as Randaugment and Mixup. This baseline model can further be optimized by adding regularization techniques like dropout or random depth, advanced optimization methods like SAM, additional data augmentation methods like Cutmix, high-resolution fine-tuning, and knowledge distillation for strong teacher supervision.
2.3. CaiT [48]
Based on previous experiences, increasing the depth of a model can allow the network to learn more complex representations. For example, models like ResNet have shown improved accuracy as the depth increases from 18 to 152 layers. However, in the case of transformers, expanding the architecture leads to difficulties in training, and instability in depth is one of the main challenges. To address this issue, CaiT proposes two improvements.
Firstly, after analyzing the interactions between different initialization methods, optimization techniques, and architectures, CaiT introduces a method called LayerScale. This method effectively enhances the training of deeper architectures. The technique known as LayerScale introduces a trainable diagonal matrix to the branches of each residual block in image transformers. This matrix is initialized near zero but not exactly zero. By incorporating this layer after each residual block, the dynamic training capabilities are enhanced, allowing for the training of deeper and higher-capacity image transformers. The LayerScale method greatly facilitates convergence and enhances the accuracy of image transformers with increased depth. Despite adding several thousand parameters to the network during training, while the overall weight count remains negligible, the LayerScale has a beneficial effect.
Another aspect of CaiT is the inclusion of class–attention layers, which effectively distinguish between the transformer layers responsible for processing patches and the class–attention layers. The primary purpose of these class–attention layers is to extract the information from processed patches into individual vectors, facilitating their use in a linear classifier. By explicitly separating these layers, CaiT prevents conflicting objectives that may arise when dealing with class embeddings. This architectural design is known as CaiT.
2.4. DeepViT [49]
Deep transformers exhibit increasingly similar attention maps as they get deeper, to the point of being nearly identical in certain layers. In essence, the feature maps in the upper layers of deep ViT models tend to exhibit similarity. This suggests that in deeper ViT models, the self-attention mechanism struggles to learn effective representations and hinders the expected performance improvement. Based on these observations, DeepViT introduces a straightforward and efficient technique known as Re-attention to enhance the variety of attention maps across various layers, all while incurring minimal computational costs and storage. By making minor adjustments to existing ViT models, this method enables the training of deeper ViT models, resulting in consistent performance enhancements. The idea behind Re-attention comes from observing that the similarity between attention maps from different heads in the same block is relatively low, even at higher layers. Therefore, a learnable transformation matrix is multiplied with the multi-head attention maps to generate new attention maps. The Re-attention layer enhances the diversity of attention across different layers. The improved ViT-32 achieves a 1.6% improvement on the ImageNet-1K dataset.
2.5. ViT with Patch Merger (ViTPM) [50]
Transformers are widely used in natural language understanding and computer vision tasks. While expanding these architectures can enhance performance, it often comes at the cost of higher computational expenses. To make large-scale models practical in real-world systems, it is necessary to reduce their computational costs. PatchMerger is a ViTs module that minimizes the number of tokens/patches fed into each transformer encoder block, preserving performance and reducing computational load. Utilizing a learnable weight matrix, it achieves this by applying a linear transformation to the input with shape N patches × D dimensions. The result is a tensor with shape M output patches × D dimensions. From this, M scores are generated and softmaxed individually. The resulting tensor, with shape M × N, is multiplied with the original input to yield an output of shape M × D. PatchMerger achieves significant acceleration across different model scales and matches the original performance in upstream and downstream tasks after fine-tuning.
2.6. Learnable Memory ViT (LMViT) [51]
Learnable memory ViT enhances visual transformer models by using learnable memory tokens. This method allows the model to adapt to new tasks with minimal parameters while selectively retaining its capabilities from previous tasks. At each layer, a set of learnable embedding vectors, known as “memory tokens”, are introduced to provide contextual information that is useful for specific datasets. Compared to traditional fine-tuning focused only on the heads, this approach enhances model accuracy by using a small number of tokens per layer, with performance being slightly below that of expensive full fine-tuning. This model proposes an attention masking method that can be extended to new downstream tasks and allows for computational reuse. In this setup, the model can execute new and old tasks as part of a single inference with a small incremental cost while achieving high parameter efficiency.
2.7. Adaptive Token Sampling ViT (ATSViT) [52]
Traditional visual transformer models have high computational costs and large parameter sizes, making them unsuitable for deployment on edge devices. While reducing the number of tokens in the network can decrease the GFLOPs, it is not possible to set the optimal tokens for different input images. During the classification process, not all image information is necessary, and depending on the image itself, some pixels in the image may be redundant or irrelevant. This model proposes the Adaptive Token Sampler (ATS) module based on self-attention matrices, which scores tokens to minimize information loss and remove redundant information from the input. This approach overcomes the limitations of introducing additional overhead in DynamicViT and achieves a reduction in computational costs and model parameters for visual transformers without the need for pre-training. The accuracy of the model is related to the number of input patches. Traditional CNNs use pooling operations, which gradually reduce the spatial resolution of the network and decrease model accuracy. Static sampling can lead to the neglect of important information or information redundancy. Therefore, this approach proposes a method for adaptively adjusting the number of tokens at different stages to achieve the goal of not ignoring important information while not wasting computational resources. The ATS module is integrated into the self-attention layer of the ViT block. It first scores the classification tokens using self-attention weights, then uses an inverse transformation to select a subset of tokens based on the scores, and finally performs soft token downsampling to remove redundant information from the output tokens with minimal information loss.
2.8. Spatial Shuffle Preprocessing
Fusing spatial and spectral features is a research hotspot in hyperspectral image classification. By processing the pixel information in the N × N neighborhood surrounding the current pixel, spatial features can be extracted and combined with spectral features to achieve high-accuracy classification. In the study of HSI classification, it is crucial to choose a specific number of labeled training sample pixels and capture the pixels within a designated neighborhood window surrounding these samples. This process involves two issues. The first issue is determining the number of training sample pixels to select. Choosing more training sample pixels can improve accuracy, but it may be challenging to obtain a large number of training sample pixels in practical applications, which reduces usability. Selecting fewer training sample pixels increases the difficulty of classification and may lead to the overfitting of deep learning models. Current research primarily focuses on how to improve classification accuracy in low-training sample scenarios. The second issue is determining the size of the neighborhood window. Using a larger neighborhood window can improve accuracy but might lead to increased dependency between training and testing samples. To mitigate this concern, a smaller neighborhood window is selected to minimize the correlation between the training and testing samples. However, this choice also reduces the number of spatial features and can potentially result in decreased accuracy.
In order to address the aforementioned issues, Wang et.al [
53] proposes a strategy called “spatial shuffle”. After obtaining the neighboring pixels of each training sample, this strategy involves randomly shuffling the positions of the pixels within the neighborhood, excluding the center pixel. Each shuffle generates a new neighborhood sample, which simulates potential pixel distribution patterns in the real world. For a 5 × 5 neighborhood, theoretically, it can produce 24! = 6.2 × 10
23 unique samples. This approach effectively alleviates the overfitting problem caused by a limited number of training samples in deep learning. Additionally, by increasing the training sample size, more diverse spatial features can be extracted, thereby improving classification accuracy.
Based on the principle of spatial shuffle and considering the requirements of the ViT for input data, the following preprocessing steps, which are the same as Ref. [
53], are performed for HSI training samples:
For a given dataset, a training sample proportion is set, such as selecting 10% of samples from each class. Then, the N × N neighborhood of each training sample is obtained, resulting in a three-dimensional data cube with dimensions of N × N × B, where B represents the number of spectral bands.
The position of the center pixel is fixed, while the other pixels within the neighborhood are randomly shuffled. Each shuffle transforms the N × N × B data cube into a two-dimensional image with a height of N × N and a width of B.
The aforementioned shuffle operation is performed 100,000/M times for each training sample from every class, where M is the number of training samples selected from that class. Consequently, each class ends up with 100,000 training samples.
After applying the shuffle operation to all training samples, a new dataset consisting of C × 100,000 training samples is formed, where C represents the total number of classes in the dataset.
Based on this new training sample dataset, various ViT models can be trained.
2.9. Ensemble Strategy
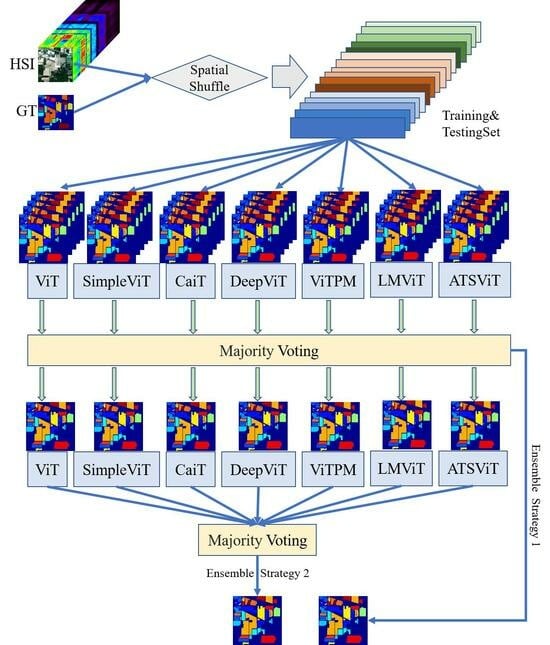
The proposed HSI classification scheme based on ensembled ViT is illustrated in
Figure 1.
The ensemble strategy described in this paper consists of two levels:
At the individual model level, due to the limited number of labels in each HSI dataset, the paper only divides the dataset into training and testing sets, without creating a separate validation set. Instead, a strategy based on majority voting is used for ensemble. Specifically, after each training epoch, the trained model is used to predict the labels for all the test samples, resulting in a predicted classification map. As the training progresses, multiple predicted classification maps are generated. After several training epochs, a pixel-level majority vote is conducted on all the generated predicted classification maps. This involves counting the occurrences of each class for each pixel across the different predicted maps and selecting the class with the highest count as the final classification result for that pixel. By employing this approach, the prediction for all the test samples can be completed. This voting-based ensemble strategy takes into account the prediction results from multiple training epochs to improve classification accuracy.
At the multiple model level, two ensemble voting strategies are employed. The first strategy (Ens1) involves conducting majority voting on the predicted classification maps from all epochs of each individual method. For instance, if there are N methods and each method undergoes M epochs of training, resulting in N × M predicted classification maps, the strategy involves performing a majority vote for each pixel of the test samples among the N × M predicted results and selecting the class with the highest number of votes as the label for that pixel. The second strategy (Ens2) starts with conducting a majority vote for each individual method, resulting in predicted classification maps for the N methods. Then, another round of majority voting is performed on the predicted classification maps of each method to obtain the final predicted classification map. The distinction between these two strategies lies in the treatment of weights for each method. Since each method may have different classification performance, the number of votes obtained through majority voting may vary for each method. For example, assuming 100 epochs of training for three methods, the highest votes obtained for each test pixel might be 90, 70, and 50 for the respective methods. In the first strategy, the weights for the three methods would be calculated as follows: 90/(90 + 70 + 50) = 9/21, 70/(90 + 70 + 50) = 7/21, and 50/(90 + 70 + 50) = 5/21. However, in the second strategy, the weights for the three methods would be equal: 1/3, 1/3, and 1/3. Therefore, there could be slight differences in the final classification accuracy values of these two strategies.
5. Conclusions
The fusion of spatial–spectral information in classification methods by combining spatial and spectral features can result in higher accuracy. This has become a topic of interest in hyperspectral image classification. Generally, larger neighborhood sizes for extracting spatial features lead to higher classification accuracy, but this also introduces the problem of overlap between the training and testing sets. ViT, by segmenting the image into independent patches, achieves a classification principle different from CNN and even surpasses CNN in terms of accuracy. This is also a current research hotspot. Combining the classification results of multiple models often yields higher accuracy than individual models. In this paper, to address the issue of spatial feature extraction, a preprocessing step called spatial shuffle is introduced. By randomly shuffling the spatial pixels, it not only simulates potential patterns in the real world but also increases the training sample size. Then, an ensemble learning framework based on various variants of ViT is constructed. Through two-level ensemble strategies, high-accuracy ensembles of multiple methods are achieved. Experimental results demonstrate that incorporating spatial shuffle as a preprocessing step effectively improves the classification accuracy of individual models, and the ensemble strategies also achieve stable high accuracy. Moreover, through ensemble strategies, valuable testing samples can be fully utilized without the need for a validation set. The proposed approach consistently achieves high classification accuracy across different training sample proportions. Compared to traditional machine learning, CNN architectures, and transformer models, the proposed ensemble strategy exhibits significant advantages on multiple datasets. According to the fundamental theory of ensemble learning, the more basic the used classifiers are, the higher the possible classification accuracy. For this paper, only seven ViT-based basic classifiers were used, and the ensemble strategy was a simple average. Therefore, using more advanced ensemble strategies may also lead to higher classification accuracy, but it may also bring higher training and inference costs. However, these costs can be greatly reduced through offline training. Our future research will focus on further optimizing ViT models and constructing more powerful individual models to enhance the fine classification capability of the ensemble framework.