A Parallel Computing Paradigm for Pan-Sharpening Algorithms of Remotely Sensed Images on a Multi-Core Computer
Abstract
:1. Introduction
2. A Short Overview of Existing Pan-Sharpening Algorithms
3. The Proposed Parallel Computing Framework
3.1. Direct Calculation of the Two Variables in the Generalized Model
3.2. Block Partition
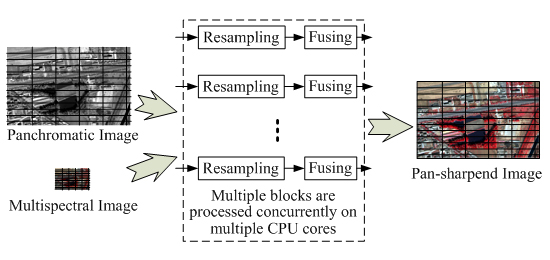
3.3. The Parallel Processing Mechanism
3.4. The Implemented Algorithms in the Framework
4. Experimental Results and Analysis
4.1. Experimental Results of Parallel Computing
4.2. Factors Determining the Maximum Speedup
4.3. The Optimal Selection of the Number of Processors
- (1)
- Linear combination: 8–12, such as IHS, PCA, Gram-Schmidt, and their variants.
- (2)
- Division operation: 14–18, such as CN, SFIM, and HPF.
- (3)
- (4)
- GLP and MRA with a higher number of decomposition levels: 16–20, such as ARSIS, context-based decision (CBD) [54].
- (5)
- Regression: 20–24, such BR, and LCM.
- (6)
4.4. Comparing with Other Multi-Core Parallel Techniques
4.5. Comparing with Commercial Software
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pohl, C.; van Genderen, J.L. Review article multisensor image fusion in remote sensing: Concepts, methods and applications. Int. J. Remote Sens 1998, 19, 823–854. [Google Scholar]
- Shettigara, V. A generalized component substitution technique for spatial enhancement of multispectral images using a higher resolution data set. Photogramm. Eng. Remote Sens 1992, 58, 561–567. [Google Scholar]
- Hill, J.; Diemer, C.; Stöver, O.; Udelhoven, T. A local correlation approach for the fusion of remote sensing data with different spatial resolutions in forestry applications. Int. Arch. Photogramm. Remote Sens 1999, 32, 4–3. [Google Scholar]
- Liu, J. Smoothing filter-based intensity modulation: A spectral preserve image fusion technique for improving spatial details. Int. J. Remote Sens. 2000, 21, 3461–3472. [Google Scholar]
- Ranchin, T.; Aiazzi, B.; Alparone, L.; Baronti, S.; Wald, L. Image fusion—The ARSIS concept and some successful implementation schemes. ISPRS J. Photogramm. Remote Sens 2003, 58, 4–18. [Google Scholar]
- Fasbender, D.; Radoux, J.; Bogaert, P. Bayesian data fusion for adaptable image pansharpening. IEEE Trans. Geosci. Remote Sens 2008, 46, 1847–1857. [Google Scholar]
- Ashraf, S.; Brabyn, L.; Hicks, B.J. Introducing contrast and luminance normalisation to improve the quality of subtractive resolution merge technique. Int. J. Image Data Fus 2013, 4, 230–251. [Google Scholar]
- Ehlers, M.; Klonus, S.; Johan Åstrand, P.; Rosso, P. Multi-sensor image fusion for pansharpening in remote sensing. Int. J. Image Data Fus 2010, 1, 25–45. [Google Scholar]
- González-Audícana, M.; Saleta, J.L.; Catalán, R.G.; García, R. Fusion of multispectral and panchromatic images using improved IHS and PCA mergers based on wavelet decomposition. IEEE Trans Geosci. Remote Sens 2004, 42, 1291–1299. [Google Scholar]
- Siddiqui, Y. The Modified IHS Method for Fusing Satellite Imagery. Proceedings of the Annual ASPRS Conference, Anchorage, AK, USA, 5–9 May 2003.
- Lee, C.A.; Gasster, S.D.; Plaza, A.; Chang, C.-I.; Huang, B. Recent developments in high performance computing for remote sensing: A review. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens 2011, 4, 508–527. [Google Scholar]
- Achalakul, T.; Taylor, S. A distributed spectral-screening PCT algorithm. J Parallel Distrib Comput 2003, 63, 373–384. [Google Scholar]
- Tehranian, S.; Zhao, Y.; Harvey, T.; Swaroop, A.; McKenzie, K. A robust framework for real-time distributed processing of satellite data. J. Parallel Distrib. Comput 2006, 66, 403–418. [Google Scholar]
- Plaza, A.; Valencia, D.; Plaza, J.; Martinez, P. Commodity cluster-based parallel processing of hyperspectral imagery. J Parallel Distrib Comput 2006, 66, 345–358. [Google Scholar]
- Plaza, A.J. Parallel techniques for information extraction from hyperspectral imagery using heterogeneous networks of workstations. J Parallel Distrib Comput 2008, 68, 93–111. [Google Scholar]
- Luo, W.; Zhang, B.; Jia, X. New improvements in parallel implementation of N-FINDR algorithm. IEEE Trans Geosci Remote Sens 2012, 50, 3648–3659. [Google Scholar]
- Winter, M.E. N-FINDR: An algorithm for fast autonomous spectral end-member determination in hyperspectral data. Proc. SPIE 1999. [Google Scholar] [CrossRef]
- Christophe, E.; Michel, J.; Inglada, J. Remote sensing processing: From multicore to GPU. IEEE J. Sel. Top. Appl Earth Observ Remote Sens 2011, 4, 643–652. [Google Scholar]
- Ma, Y.; Wang, L.; Liu, D.; Yuan, T.; Liu, P.; Zhang, W. Distributed data structure templates for data-intensive remote sensing applications. Concurr. Comput.: Pract Exp 2013, 25, 1784–1797. [Google Scholar]
- Ma, Y.; Wang, L.; Liu, D.; Liu, P.; Wang, J.; Tao, J. Generic Parallel Programming for Massive Remote Sensing Data Processing. Proceedings of the IEEE International Conference on Cluster Computing (CLUSTER), Beijng, China, 24–28 September 2012; pp. 420–428.
- Wei, J.; Liu, D.; Wang, L. A general metric and parallel framework for adaptive image fusion in clusters. Concurr. Comput.: Pract Exp 2014, 26, 1375–1387. [Google Scholar]
- Remon, A.; Sanchez, S.; Paz, A.; Quintana-Orti, E.S.; Plaza, A. Real-time endmember extraction on multicore processors. IEEE Geosci Remote Sens Lett 2011, 8, 924–928. [Google Scholar]
- Bernabe, S.; Sanchez, S.; Plaza, A.; Lopez, S.; Benediktsson, J.A.; Sarmiento, R. Hyperspectral unmixing on GPUs and multi-core processors: A comparison. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens 2013, 6, 1386–1398. [Google Scholar]
- Yang, J.H.; Zhang, J.X.; Li, H.T.; Sun, Y.S.; Pu, P.X. Pixel level fusion methods for remote sensing images: A current review. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2010, 38, 680–686. [Google Scholar]
- Alparone, L.; Wald, L.; Chanussot, J.; Thomas, C.; Gamba, P.; Bruce, L.M. Comparison of pansharpening algorithms: Outcome of the 2006 GRS-S data-fusion contest. IEEE Trans. Geosci. Remote Sens 2007, 45, 3012–3021. [Google Scholar]
- Nikolakopoulos, K.G. Comparison of nine fusion techniques for very high resolution data. Photogramm. Eng. Remote Sens 2008, 74, 647–659. [Google Scholar]
- Dahiya, S.; Garg, P.K.; Jat, M.K. A comparative study of various pixel-based image fusion techniques as applied to an urban environment. Int. J. Image Data Fus 2013, 4, 197–213. [Google Scholar]
- Ghosh, A.; Joshi, P. Assessment of pan-sharpened very high-resolution WorldView-2 images. Int. J. Remote Sens 2013, 34, 8336–8359. [Google Scholar]
- Jawak, S.D.; Luis, A.J. A comprehensive evaluation of PAN-Sharpening algorithms coupled with resampling methods for image synthesis of very high resolution remotely sensed satellite data. Adv. Remote Sens 2013, 2, 332–344. [Google Scholar]
- Witharana, C.; Civco, D.L.; Meyer, T.H. Evaluation of pansharpening algorithms in support of earth observation based rapid-mapping workflows. Appl. Geogr. 2013, 37, 63–87. [Google Scholar]
- Alimuddin, I.; Sumantyo, J.T.S.; Kuze, H. Assessment of pan-sharpening methods applied to image fusion of remotely sensed multi-band data. Int. J. Appl. Earth Observ. Geoinf 2012, 18, 165–175. [Google Scholar]
- Yusuf, Y.; Sri Sumantyo, J.T.; Kuze, H. Spectral information analysis of image fusion data for remote sensing applications. Geocarto Int 2012, 28, 291–310. [Google Scholar]
- Gamba, P. Image and data fusion in remote sensing of urban areas: Status issues and research trends. Int. J. Image Data Fus 2014, 5, 2–12. [Google Scholar]
- Carper, W.J. The use of intensity-hue saturation transformations for merging SPOT panchromatic and multispectral image data. Photogramm. Eng. Remote Sens 1990, 56, 459–467. [Google Scholar]
- Zhou, X.; Liu, J.; Liu, S.; Cao, L.; Zhou, Q.; Huang, H. A. GIHS-based spectral preservation fusion method for remote sensing images using edge restored spectral modulation. ISPRS J. Photogramm. Remote Sens 2014, 88, 16–27. [Google Scholar]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. US Patents 6011875. 4 January 2000. [Google Scholar]
- Tu, T.-M.; Huang, P.S.; Hung, C.-L.; Chang, C.-P. A fast intensity-hue-saturation fusion technique with spectral adjustment for IKONOS imagery. IEEE Geosci. Remote Sens. Lett 2004, 1, 309–312. [Google Scholar]
- Choi, M. A new intensity-hue-saturation fusion approach to image fusion with a tradeoff parameter. IEEE Trans.Geosci. Remote Sens 2006, 44, 1672–1682. [Google Scholar]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS+ Pan data. IEEE Trans. Geosci. Remote Sens 2007, 45, 3230–3239. [Google Scholar]
- Yee, L.; Liu, J.; Zhang, J. An improved adaptive Intensity–Hue–Saturation method for the fusion of remote sensing images. IEEE Geosci. Remote Sens. Lett 2014, 11, 985–989. [Google Scholar]
- González-Audícana, M.; Otazu, X.; Fors, O.; Alvarez-Mozos, J. A low computational-cost method to fuse IKONOS images using the spectral response function of its sensors. IEEE Trans. Geosci. Remote Sens 2006, 44, 1683–1691. [Google Scholar]
- Švab, A.; Oštir, K. High-resolution image fusion: Methods to preserve spectral and spatial resolution. Photogramm. Eng. Remote Sens 2006, 72, 565–572. [Google Scholar]
- Thomas, C.; Ranchin, T.; Wald, L.; Chanussot, J. Synthesis of multispectral images to high spatial resolution: A critical review of fusion methods based on remote sensing physics. IEEE Trans. Geosci. Remote Sens 2008, 46, 1301–1312. [Google Scholar]
- Malpica, J.A. Hue adjustment to IHS pan-sharpened IKONOS imagery for vegetation enhancement. IEEE Geosci. Remote Sens. Lett 2007, 4, 27–31. [Google Scholar]
- Ling, Y.; Ehlers, M.; Usery, E.L.; Madden, M. FFT-enhanced IHS transform method for fusing high-resolution satellite images. ISPRS J. Photogramm. Remote Sens 2007, 61, 381–392. [Google Scholar]
- Vrabel, J. Multispectral imagery advanced band sharpening study. Photogramm. Eng. Remote Sens 2000, 66, 73–80. [Google Scholar]
- Zhang, Y. A new merging method and its spectral and spatial effects. Int. J. Remote Sens 1999, 20, 2003–2014. [Google Scholar]
- Gangkofner, U.G.; Pradhan, P.S.; Holcomb, D.W. Optimizing the high-pass filter addition technique for image fusion. Photogramm. Eng. Remote Sens 2008, 74, 1107–1118. [Google Scholar]
- Garguet-Duport, B.; Girel, J.; Chassery, J.-M.; Patou, G. The use of multiresolution analysis and wavelets transform for merging SPOT panchromatic and multispectral image data. Photogramm. Eng. Remote Sens 1996, 62, 1057–1066. [Google Scholar]
- Nunez, J.; Otazu, X.; Fors, O.; Prades, A.; Pala, V.; Arbiol, R. Multiresolution-based image fusion with additive wavelet decomposition. IEEE Trans. Geosci. Remote Sens 1999, 37, 1204–1211. [Google Scholar]
- Amolins, K.; Zhang, Y.; Dare, P. Wavelet based image fusion techniques—An introduction, review and comparison. ISPRS J. Photogramm. Remote Sens 2007, 62, 249–263. [Google Scholar]
- El Ejaily, A.; Eltohamy, F.; Hamid, M.; Ismail, G. An image fusion method using DT-CWT and average gradient. Int. J. Comput. Sci. Mobile Comput 2014, 3, 272–280. [Google Scholar]
- Daza, R.J.M.; Ruiz, C.P.; Aguilar, L.J. Two-dimensional fast Haar wavelet transform for satellite-image fusion. J. Appl. Remote Sens 2013. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A. Context-driven fusion of high spatial and spectral resolution images based on oversampled multiresolution analysis. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2300–2312. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and Pan imagery. Photogramm. Eng. Remote Sens 2006, 72, 591–596. [Google Scholar]
- Garzelli, A.; Nencini, F. Interband structure modeling for Pan-sharpening of very high-resolution multispectral images. Inf. Fus 2005, 6, 213–224. [Google Scholar]
- Pradhan, P.S.; King, R.L.; Younan, N.H.; Holcomb, D.W. Estimation of the number of decomposition levels for a wavelet-based multiresolution multisensor image fusion. IEEE Trans. Geosci. Remote Sens 2006, 44, 3674–3686. [Google Scholar]
- Chen, S.; Su, H.; Tian, J.; Zhan, C. Best tradeoff for remote sensing image fusion based on three-dimensional variation and à trous wavelet. Appl. Remote Sens 2013. [Google Scholar] [CrossRef]
- Shah, V.P.; Younan, N.H.; King, R.L. An efficient pan-sharpening method via a combined adaptive PCA approach and contourlets. IEEE Trans. Geosci. Remote Sens 2008, 46, 1323–1335. [Google Scholar]
- Dong, Z.; Wang, Z.; Liu, D.; Zhang, B.; Zhao, P.; Tang, X.; Jia, M. SPOT5 multi-spectral (MS) and panchromatic (PAN) image fusion using an improved wavelet method based on local algorithm. Comput. Geosci 2013, 60, 134–141. [Google Scholar]
- Chibani, Y.; Houacine, A. The joint use of IHS transform and redundant wavelet decomposition for fusing multispectral and panchromatic images. Int. J. Remote Sens 2002, 23, 3821–3833. [Google Scholar]
- Shi, W.; Zhu, C.; Zhu, S. Fusing IKONOS images by a four-band wavelet transformation method. Photogramm. Eng. Remote Sens 2007. [Google Scholar] [CrossRef]
- Choi, J.; Yeom, J.; Chang, A.; Byun, Y.; Kim, Y. Hybrid pansharpening algorithm for high spatial resolution satellite imagery to improve spatial quality. IEEE Geosci. Remote Sens. Lett 2013, 10, 490–494. [Google Scholar]
- Otazu, X.; Gonzalez-Audicana, M.; Fors, O.; Nunez, J. Introduction of sensor spectral response into image fusion methods. Application to wavelet-based methods. IEEE Trans. Geosci. Remote Sens 2005, 43, 2376–2385. [Google Scholar]
- Ballester, C.; Caselles, V.; Igual, L.; Verdera, J.; Rougé, B. A variational model for P+ XS image fusion. Int. J. Comput. Vis 2006, 69, 43–58. [Google Scholar]
- Joshi, M.; Jalobeanu, A. MAP estimation for multiresolution fusion in remotely sensed images using an IGMRF prior model. IEEE Trans. Geosci. Remote Sens 2010, 48, 1245–1255. [Google Scholar]
- Joshi, M.V.; Bruzzone, L.; Chaudhuri, S. A model-based approach to multiresolution fusion in remotely sensed images. IEEE Trans. Geosci. Remote Sens 2006, 44, 2549–2562. [Google Scholar]
- Aanæs, H.; Sveinsson, J.R.; Nielsen, A.A.; Bovith, T.; Benediktsson, J.A. Model-based satellite image fusion. IEEE Trans. Geosci. Remote Sens 2008, 46, 1336–1346. [Google Scholar]
- Garzelli, A.; Nencini, F.; Capobianco, L. Optimal MMSE pan sharpening of very high resolution multispectral images. IEEE Trans. Geosci. Remote Sens 2008, 46, 228–236. [Google Scholar]
- Li, Z.; Leung, H. Fusion of multispectral and panchromatic images using a restoration-based method. IEEE Trans. Geosci. Remote Sens 2009, 47, 1482–1491. [Google Scholar]
- Duran, J.; Buades, A.; Coll, B.; Sbert, C. Implementation of nonlocal pansharpening image fusion. Image Process. On Line 2014. [Google Scholar] [CrossRef]
- Zhang, Y. Understanding image fusion. Photogramm. Eng. Remote Sens 2004, 70, 657–661. [Google Scholar]
- Li, S.; Yang, B. A new pan-sharpening method using a compressed sensing technique. IEEE Trans. Geosci. Remote Sens 2011, 49, 738–746. [Google Scholar]
- Zhu, X.X.; Bamler, R. A sparse image fusion algorithm with application to pan-sharpening. IEEE Trans. Geosci. Remote Sens 2013, 51, 2827–2836. [Google Scholar]
- Tu, T.-M.; Su, S.-C.; Shyu, H.-C.; Huang, P.S. A new look at IHS-like image fusion methods. Inf. Fus. 2001, 2, 177–186. [Google Scholar]
- Wang, Z.; Ziou, D.; Armenakis, C.; Li, D.; Li, Q. A comparative analysis of image fusion methods. IEEE Trans. Geosci. Remote Sens 2005, 43, 1391–1402. [Google Scholar]
- Zhang, J.X.; Yang, J.H.; Li, H.T.; Yan, Q. Generalized model for remotely sensed data pixel-level fusion. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2008, 37, 1051–1056. [Google Scholar]
- Palubinskas, G. Fast, simple, and good pan-sharpening method. J. Appl. Remote Sens 2013. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, B.; Yu, L. Intermodality models in pan-sharpening: Analysis based on remote sensing physics. Int. J. Remote Sens 2014, 35, 515–531. [Google Scholar]
- Zhang, J.X.; Yang, J.H. Data Fusion. In Advanced Remote Sensing: Terrestrial Information Extraction and Applications; Liang, S., Li, X., Wang, J., Eds.; Academic Press: San Diego, CA, USA, 2012; pp. 91–109. [Google Scholar]
- Nicolescu, C.; Jonker, P. A data and task parallel image processing environment. Parallel Comput. 2002, 28, 945–965. [Google Scholar]
- Zhang, J.X.; Yang, J.H.; Zhao, Z.; Li, H.T.; Zhang, Y.H. Block-regression based fusion of optical and SAR imagery for feature enhancement. Int. J. Remote Sens 2010, 31, 2325–2345. [Google Scholar]
- Gropp, W.; Lusk, E.; Doss, N.; Skjellum, A. A high-performance, portable implementation of the MPI message passing interface standard. Parallel Comput 1996, 22, 789–828. [Google Scholar]
- Wilkinson, B.; Allen, C.M. Parallel Programming; Prentice Hall: New Jersey, NJ, USA, 1999. [Google Scholar]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. Lett 2002, 9, 81–84. [Google Scholar]
- Möller, M.; Wittman, T.; Bertozzi, A.L.; Burger, M. A variational approach for sharpening high dimensional images. SIAM J. Imag. Sci 2012, 5, 150–178. [Google Scholar]
- Choi, Y.; Sharifahmadian, E.; Latifi, S. Fusion and quality analysis for remote sensing images using contourlet transform. Proc. SPIE 2013. [Google Scholar] [CrossRef]
- Zhou, J.; Civco, D.; Silander, J. A wavelet transform method to merge Landsat TM and SPOT panchromatic data. Int. J. Remote Sens 1998, 19, 743–757. [Google Scholar]
- Saeedi, J.; Faez, K. A new pan-sharpening method using multiobjective particle swarm optimization and the shiftable contourlet transform. ISPRS J. Photogramm. Remote Sens 2011, 66, 365–381. [Google Scholar]
- Lemoine, G.; Giovalli, M. Geo-correction of high-resolution imagery using fast template matching on a GPU in emergency mapping contexts. Remote Sens. 2013, 5, 4488–4502. [Google Scholar]







| Fusion Algorithm | α(k,i,j) | δ(i,j) |
| PCA | ωk1 | pan(i,j)–pc1(i,j) |
| IHS | 1 | pan(i,j)–I(i,j) |
| RVS | ωk1 | |
| SFIM | pan(i,j)− syn(i,j) where syn = f*pan | |
| CN | ||
| à trous | Additive: 1 Minimum spectral distortion: | where |
| GLP | Minimum spectral distortion:
Context-based decision: | |
| Fusion algorithm combining wavelet decomposition with PCA transform | ωk1 | where |
| Fusion algorithm combining wavelet decomposition with IHS transform | 1 | where |
| LCM | bk where | |
| ARSIS | Context-based decision: | |
| Block regression | pan(i,j) − syn(i,j), For each block: |
| Dell Precision T7500 workstation |
| CPUs: Two Intel Xeon X5675 CPU, 3.06 GHz, 6 cores per CPU, 24 virtual CPU cores using hyper-threading technology |
| RAM: 48 GB Disk and file system: A Solid-State Drive (SSD) with 120 G, NTFS file system |
| OS: Windows 7 Professional, Service Pack 1, 64-bit |
| Image Type | File Size | Image Size | Image File Format | Data Type | Bands |
|---|---|---|---|---|---|
| Panchromatic | 777 MB | 28,820 × 28,155 | ERDAS IMAGINE | Unsigned 8-bit | 1 |
| Multispectral | 196 MB | 7706 × 7068 | ERDAS IMAGINE | Unsigned 8-bit | 4 |
| Fusion results | 3.02 GB | 28,820 × 28,155 | ERDAS IMAGINE | Unsigned 8-bit | 4 |
| Number of Processors | 1 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IHS | Time | 286.26 | 252.93 | 102.14 | 73.39 | 65.90 | 65.54 | 66.81 | 64.71 | 66.38 | |||
| Speedup | 1.0 | 1.1 | 2.8 | 3.9 | 4.3 | 4.4 | 4.3 | 4.4 | 4.3 | ||||
| PCA | Time | 321.37 | 275.60 | 128.62 | 103.42 | 98.58 | 98.33 | 99.39 | 103.32 | 105.98 | |||
| Speedup | 1.0 | 1.2 | 2.5 | 3.1 | 3.3 | 3.3 | 3.2 | 3.1 | 3.0 | ||||
| CN | Time | 784.38 | 755.76 | 272.87 | 165.83 | 126.75 | 108.30 | 96.03 | 88.40 | 87.03 | 83.03 | ||
| Speedup | 1.0 | 1.0 | 2.9 | 4.7 | 6.2 | 7.2 | 8.2 | 8.9 | 9.0 | 9.4 | |||
| SFIM | Time | 685.80 | 678.66 | 236.03 | 149.31 | 113.76 | 98.86 | 86.89 | 82.86 | 80.41 | 76.15 | ||
| Speedup | 1.0 | 1.0 | 2.9 | 4.6 | 6.0 | 6.9 | 7.9 | 8.3 | 8.5 | 9.0 | |||
| BR | Time | 1683.76 | 1624.68 | 986.27 | 521.57 | 334.61 | 374.68 | 280.49 | 294.53 | 282.90 | 269.05 | 176.27 | |
| Speedup | 1.0 | 1.0 | 1.7 | 3.2 | 5.0 | 4.5 | 6.0 | 5.7 | 6.0 | 6.3 | 9.6 | ||
| LCM | Time | 7957.20 | 7948.99 | 3145.59 | 1805.61 | 1252.67 | 1103.82 | 877.48 | 811.57 | 733.28 | 658.81 | 698.27 | 573.81 |
| Speedup | 1.0 | 1.0 | 2.5 | 4.4 | 6.4 | 7.2 | 9.1 | 9.8 | 10.9 | 12.1 | 11.4 | 13.9 | |
| à trous | Time | 414.66 | 371.07 | 142.11 | 97.83 | 80.50 | 73.62 | 71.21 | 69.38 | 68.08 | |||
| Speedup | 1.0 | 1.1 | 2.9 | 4.2 | 5.2 | 5.6 | 5.8 | 6.0 | 6.1 | ||||
| PCA à trous | Time | 419.41 | 382.81 | 151.34 | 105.45 | 86.03 | 80.31 | 76.96 | 77.62 | 84.28 | |||
| Speedup | 1.0 | 1.1 | 2.8 | 4.0 | 4.9 | 5.2 | 5.4 | 5.4 | 5.0 | ||||
| Number of Processors | Processor Rank | Accumulated Receiving Time | Accumulated Writing Time | Total Time |
|---|---|---|---|---|
| 2 | 0 | 707.85 | 44.44 | 752.97 |
| 4 | 0 | 205.40 | 64.86 | 270.91 |
| 6 | 0 | 98.87 | 67.41 | 166.94 |
| 8 | 0 | 56.00 | 73.06 | 129.78 |
| 10 | 0 | 37.12 | 75.81 | 113.59 |
| 12 | 0 | 25.73 | 77.54 | 103.98 |
| 14 | 0 | 20.27 | 76.41 | 97.37 |
| 16 | 0 | 16.69 | 78.55 | 96.02 |
| 18 | 0 | 13.35 | 77.59 | 91. 73 |
| 20 | 0 | 18.91 | 79.67 | 99.37 |
| 22 | 0 | 10.41 | 79.02 | 90.22 |
| Number of Processors | Processor Rank | Accumulated Reading Time | Accumulated Computing Time | Accumulated Sending Time | Total Time |
|---|---|---|---|---|---|
| 2 | 1 | 5.6 | 744.86 | 1.83 | 752.97 |
| 4 | 1 | 2.48 | 261.10 | 5.97 | 270.91 |
| 6 | 5 | 1.60 | 155.64 | 9.04 | 166.94 |
| 8 | 5 | 1.18 | 110.59 | 14.75 | 129.78 |
| 10 | 8 | 1.10 | 90.01 | 19.53 | 113.59 |
| 12 | 6 | 1.22 | 72.81 | 26.18 | 103.98 |
| 14 | 13 | 1.25 | 64.84 | 29.49 | 97.37 |
| 16 | 4 | 1.24 | 59.42 | 32.76 | 96.02 |
| 18 | 13 | 1.56 | 52.89 | 33.92 | 91.73 |
| 20 | 2 | 1.54 | 61.65 | 30.08 | 99.37 |
| 22 | 14 | 1.39 | 47.64 | 38.95 | 90.22 |
| Algorithm | Number of Processors | ||
|---|---|---|---|
| 1 | 8 | 12 | |
| IHS in the framework | 286.26 | 65.90 | 66.81 |
| Mod. IHS (ERDAS) | 2147.9 | ||
| PCA in the framework | 321.37 | 98.58 | 99.39 |
| PCA (ERDAS) | 1376.2 | ||
| PC Spectral Sharpening (ENVI 4.7) | 600.20 | ||
| CN in the framework | 784.38 | 126.75 | 96.03 |
| Color Normalized (ENVI 4.7) | 756.67 | ||
| Algorithm | Band | ||||
|---|---|---|---|---|---|
| Blue | Green | Red | NIR | Average | |
| IHS in the framework | 0.7346 | 0.8928 | 0.9009 | 0.9494 | 0.9144 |
| Mod. IHS (ERDAS) | 0.8905 | 0.9303 | 0.8851 | 0.9020 | |
| PCA in the framework | 0.6008 | 0.8301 | 0.8482 | 0.9894 | 0.8171 |
| PCA (ERDAS) | 0.8513 | 0.8488 | 0.8549 | 0.9374 | 0.8731 |
| PC Spectral Sharpening (ENVI 4.7) | 0.8774 | 0.8707 | 0.8783 | 0.9453 | 0.8929 |
| CN in the framework | 0.8206 | 0.8739 | 0.9301 | 0.9398 | 0.9146 |
| Color Normalized (ENVI 4.7) | 0.8585 | 0.9143 | 0.9175 | 0.8968 | |
| Algorithm | IHS in the Framework | Mod. IHS (ERDAS) | PCA in the Framework | PCA (ERDAS) | PC Spectral Sharpening (ENVI 4.7) | CN in the Framework | Color Normalized (ENVI 4.7) |
|---|---|---|---|---|---|---|---|
| UIQI | 0.9866 | 0.7339 | 0.7400 | 0.9556 | 0.9757 | 0.9739 | 0.2768 |
| Algorithm | Band | ||||
|---|---|---|---|---|---|
| Blue | Green | Red | NIR | Average | |
| IHS in the framework | 0.9955 | 0.9977 | 0.9971 | 0.9892 | 0.9947 |
| Mod. IHS (ERDAS) | 0.9457 | 0.9201 | 0.9312 | 0.9323 | |
| PCA in the framework | 0.9965 | 0.9969 | 0.9981 | 0.8655 | 0.9643 |
| PCA (ERDAS) | 0.9971 | 0.9987 | 0.9972 | 0.9917 | 0.9962 |
| PC Spectral Sharpening (ENVI 4.7) | 0.9940 | 0.9984 | 0.9976 | 0.9847 | 0.9937 |
| CN in the framework | 0.9892 | 0.9942 | 0.9865 | 0.9734 | 0.9847 |
| Color Normalized (ENVI 4.7) | 0.9907 | 0.9846 | 0.9771 | 0.9841 | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yang, J.; Zhang, J.; Huang, G. A Parallel Computing Paradigm for Pan-Sharpening Algorithms of Remotely Sensed Images on a Multi-Core Computer. Remote Sens. 2014, 6, 6039-6063. https://doi.org/10.3390/rs6076039
Yang J, Zhang J, Huang G. A Parallel Computing Paradigm for Pan-Sharpening Algorithms of Remotely Sensed Images on a Multi-Core Computer. Remote Sensing. 2014; 6(7):6039-6063. https://doi.org/10.3390/rs6076039
Chicago/Turabian StyleYang, Jinghui, Jixian Zhang, and Guoman Huang. 2014. "A Parallel Computing Paradigm for Pan-Sharpening Algorithms of Remotely Sensed Images on a Multi-Core Computer" Remote Sensing 6, no. 7: 6039-6063. https://doi.org/10.3390/rs6076039
APA StyleYang, J., Zhang, J., & Huang, G. (2014). A Parallel Computing Paradigm for Pan-Sharpening Algorithms of Remotely Sensed Images on a Multi-Core Computer. Remote Sensing, 6(7), 6039-6063. https://doi.org/10.3390/rs6076039