Seasonal Variations of the Relative Optical Air Mass Function for Background Aerosol and Thin Cirrus Clouds at Arctic and Antarctic Sites
Abstract
:1. Introduction
| Ablesun-Photometer Model | Arctic Stations | Antarctic Stations | Peak-Wavelengths (nm) | References |
|---|---|---|---|---|
| Cimel CE-318 sun-photometer model of the AERONET and AEROCAN networks | Barrow (Alaska, USA); Resolute Bay (Nunavut, Canada); Eureka 0PAL (Nunavut, Canada); Eureka PEARL (Nunavut, Canada); Thule (North-Western Greenland); Ittoqqortoormiit (Eastern Greenland); Hornsund (Spitsbergen, Svalbard); Andenes (Norway); Sodankylä (Finland); Tiksi (NE Siberia, Russia) | Marambio (Argentina); Vechernaya Hill (Belarus); Utsteinen Ridge (Belgium); McMurdo (USA); Dome C (France/Italy); South Pole (USA) | 340, 380, 440, 500, 675, 870, 1020 | Holben et al. [2] |
| Precision Filter Radiometer PFR of the GAW-PFR Network, PMOD/WRC (Davos, Switzerland) | Summit (Central Greenland); Ny-Ålesund (Spitsbergen, Svalbard); Kiruna (Sweden); Sodankylä (Finland) | Troll (Norway) | 367.6, 367.7, 368.0, 368.7, 368.9, 411.4, 411.9, 412.0, 412.1, 499.7, 500.0, 500.5, 500.6, 861.6, 862.0, 862.2, 862.5 | Wehrli [8] |
| Carter Scott SP01, SP01-A, SP02 and SP022 models of the GMD/NOAA (Boulder, Colorado, USA) | Barrow (Alaska, USA); Alert (Nunavut, (Canada) | Dome C (France/Italy); South Pole (USA) | 367, 368, 412, 413, 500, 610, 675, 778, 862, 865, 1050 | Stone [9] |
| Prede POM-01L and POM-02L models of the NIPR (Tokyo, Japan); Prede POM-02L model of the ISAC-CNR Institute (Rome, Italy), and Prede POM-01L model of the British Antarctic Survey (BAS) (Cambridge, UK) of the SKYNET network | Ny-Ålesund (Spitsbergen, Svalbard) | Syowa (Japan); Rothera (UK); Halley (UK); Mario Zucchelli (Italy) | 315, 340, 380, 400, 500, 675, 870, 1020, 1627, 2200 | Shiobara et al. [10], di Carmine et al. [11] |
| SP1A and SP2H sun-photometer models and STAR 01 star-photometer of the Alfred Wegener Institute (AWI, Bremenhaven, Germany) | Ny-Ålesund (Spitsbergen, Svalbard) | Neumayer (Germany) | 351, 367, 371, 380, 390, 413, 416, 441, 443, 500, 501, 531, 532, 605, 609, 673, 675, 776, 778, 862, 864, 1023, 1025, 1045, 1046, 1062 | Herber et al. [12] |
| ABAS sun-photometer of the Alfred Wegener Institute (AWI, Bremenhaven, Germany) and the Arctic and Antarctic Research Institute (AARI, St. Petersburg, Russia) | - | Neumayer (Germany); Mirny (Russia) | 395, 408, 479, 581, 651, 789, 873, 1041 | Leiterer and Weller [13], Radionov et al. [14] |
| Portable SPM models of the Institute of Atmospheric Optics (IAO), Siberian Branch (SB), Russian Academy of Sciences (RAS) (Tomsk, Russia) | Barentsburg (Spitsbergen, Svalbard) | Mirny (Russia) | 339, 340, 379, 380, 442, 443, 499, 500, 547, 548, 675, 676, 871, 1019, 1020, 1240, 1244, 1553, 1555, 2134 | Sakerin et al. [15] |
| Handheld Microtops II of the Space Physics Laboratory, Trivandrum (India), the IAO-SB-RAS (Tomsk, Russia), the AARI Institute (St. Petersburg, Russia), and the OPAR Institute, University of Réunion, Saint Denis de la Réunion (France) | Ny-Ålesund (Spitsbergen, Svalbard) | Mirny (Russia); Novolazarevskaya (Russia); Dome C (France/Italy) | 379, 440, 441, 500, 674, 675, 868, 870 | Smirnov et al. [4] |
| EKO MS-110 of the Japan Meteorological Agency (JMA) (Tokyo, Japan) | -- | Syowa (Japan) | 368, 500, 675, 778, 862 | Ohno [5] |
| UVISIR-2, FISBAT and ASP-15WL sun-photometer models of the ISAC-CNR Institute (Bologna, Italy) | -- | Mario Zucchelli (Italy) | 320.2, 321.0, 335.3, 342.0, 359.8, 370.0, 381.0, 400.2, 401.3, 411.5, 441.5, 450.5, 459.6, 499.5, 500.6, 505.9, 550.0, 551.0, 610.0, 669.7, 671.3, 672.5, 774.6, 780.0, 861.2, 865.2, 868.0, 1025.7, 1040.6, 1047.4 | Tomasi et al. [6,16,17] |
2. The Atmospheric Model used to Calculate the Relative Optical Air Mass Functions and Determination of the Vertical Profiles of Aerosol Volume Extinction Coefficient

3. Calculations of Relative Optical Air Mass Function for Various Aerosol Types and Cloud Particle Layers
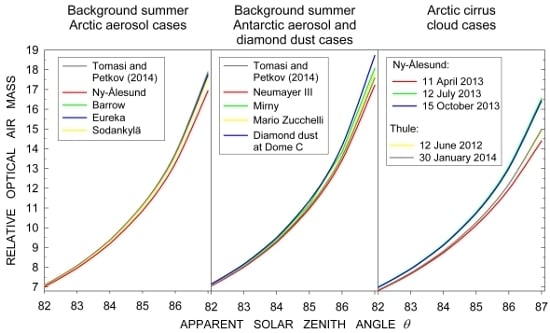
3.1. Background Arctic Aerosol Cases based on the Koldewey-Aerosol-Raman Lidar-System Measurements at Ny-Ålesund

| θ (°) | Ny-Ålesund | Barrow | Eureka | Sodankylä | Tomasi and Petkov [22] | |||
|---|---|---|---|---|---|---|---|---|
| January Average | April Average | June-July Average | October−December Average | Summer Average | Summer Average | Summer Average | ||
| 0 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 10 | 1.0154 | 1.0154 | 1.0154 | 1.0154 | 1.0154 | 1.0154 | 1.0154 | 1.0154 |
| 20 | 1.0641 | 1.0641 | 1.0641 | 1.0641 | 1.0641 | 1.0641 | 1.0641 | 1.0641 |
| 30 | 1.1545 | 1.1545 | 1.1545 | 1.1545 | 1.1546 | 1.1546 | 1.1546 | 1.1546 |
| 40 | 1.3050 | 1.3049 | 1.3049 | 1.3050 | 1.3051 | 1.3051 | 1.3051 | 1.3052 |
| 50 | 1.5547 | 1.5546 | 1.5546 | 1.5546 | 1.5551 | 1.5551 | 1.5550 | 1.5552 |
| 55 | 1.7418 | 1.7417 | 1.7416 | 1.7417 | 1.7424 | 1.7424 | 1.7423 | 1.7426 |
| 60 | 1.9972 | 1.9970 | 1.9969 | 1.9971 | 1.9982 | 1.9983 | 1.9981 | 1.9986 |
| 65 | 2.3611 | 2.3608 | 2.3606 | 2.3609 | 2.3630 | 2.3631 | 2.3628 | 2.3636 |
| 70 | 2.9135 | 2.9129 | 2.9126 | 2.9131 | 2.9173 | 2.9176 | 2.9169 | 2.9186 |
| 72 | 3.2218 | 3.2210 | 3.2206 | 3.2213 | 3.2271 | 3.2274 | 3.2265 | 3.2288 |
| 74 | 3.6076 | 3.6064 | 3.6058 | 3.6068 | 3.6151 | 3.6156 | 3.6143 | 3.6175 |
| 75 | 3.8389 | 3.8375 | 3.8368 | 3.8380 | 3.8481 | 3.8487 | 3.8471 | 3.8510 |
| 76 | 4.1031 | 4.1014 | 4.1005 | 4.1020 | 4.1144 | 4.1151 | 4.1131 | 4.1179 |
| 77 | 4.4075 | 4.4052 | 4.4041 | 4.4061 | 4.4214 | 4.4223 | 4.4198 | 4.4259 |
| 78 | 4.7617 | 4.7588 | 4.7574 | 4.7599 | 4.7793 | 4.7804 | 4.7772 | 4.7849 |
| 79 | 5.1789 | 5.1750 | 5.1733 | 5.1765 | 5.2014 | 5.2029 | 5.1988 | 5.2087 |
| 80 | 5.6771 | 5.6718 | 5.6697 | 5.6739 | 5.7065 | 5.7086 | 5.7030 | 5.7162 |
| 81 | 6.2820 | 6.2745 | 6.2717 | 6.2776 | 6.3213 | 6.3242 | 6.3166 | 6.3344 |
| 82 | 7.0311 | 7.0201 | 7.0165 | 7.0249 | 7.0852 | 7.0894 | 7.0786 | 7.1035 |
| 83 | 7.9817 | 7.9647 | 7.9601 | 7.9725 | 8.0586 | 8.0653 | 8.0490 | 8.0853 |
| 84 | 9.2259 | 9.1978 | 9.1921 | 9.2115 | 9.3395 | 9.3507 | 9.3248 | 9.3804 |
| 85 | 10.921 | 10.870 | 10.864 | 10.897 | 11.097 | 11.117 | 11.073 | 11.163 |
| 86 | 13.358 | 13.257 | 13.254 | 13.314 | 13.647 | 13.690 | 13.604 | 13.765 |
| 87 | 17.149 | 16.917 | 16.934 | 17.061 | 17.657 | 17.765 | 17.571 | 17.893 |
3.2. Background Summer Arctic Aerosol Cases based on the Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observations over Barrow, Eureka and Sodankylä

3.3. Background Austral Summer Antarctic Aerosol Cases at Neumayer III, Mirny and Mario Zucchelli from CALIPSO Observations
| θ (°) | Summer background Antarctic Aerosol ma(θ) | Diamond Dust Case | Tomasi and Petkov [22] | ||
|---|---|---|---|---|---|
| Neumayer III (Seasonal Average) | Mirny (Seasonal Average) | Mario Zucchelli (Seasonal Average) | mdd(θ) | mbAa(θ) | |
| 0 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 10 | 1.0154 | 1.0154 | 1.0154 | 1.0154 | 1.0154 |
| 20 | 1.0641 | 1.0641 | 1.0641 | 1.0642 | 1.0641 |
| 30 | 1.1545 | 1.1546 | 1.1546 | 1.1547 | 1.1546 |
| 40 | 1.3050 | 1.3052 | 1.3052 | 1.3053 | 1.3051 |
| 50 | 1.5548 | 1.5553 | 1.5551 | 1.5555 | 1.5550 |
| 55 | 1.7420 | 1.7427 | 1.7425 | 1.7431 | 1.7423 |
| 60 | 1.9976 | 1.9987 | 1.9983 | 1.9995 | 1.9981 |
| 65 | 2.3618 | 2.3639 | 2.3632 | 2.3652 | 2.3627 |
| 70 | 2.9149 | 2.9192 | 2.9178 | 2.9219 | 2.9168 |
| 72 | 3.2238 | 3.2297 | 3.2277 | 3.2334 | 3.2263 |
| 74 | 3.6104 | 3.6188 | 3.6160 | 3.6241 | 3.6140 |
| 75 | 3.8423 | 3.8525 | 3.8491 | 3.8591 | 3.8467 |
| 76 | 4.1072 | 4.1198 | 4.1156 | 4.1279 | 4.1126 |
| 77 | 4.4125 | 4.4282 | 4.4230 | 4.4383 | 4.4193 |
| 78 | 4.7680 | 4.7879 | 4.7813 | 4.8007 | 4.7766 |
| 79 | 5.1869 | 5.2126 | 5.2040 | 5.2292 | 5.1980 |
| 80 | 5.6874 | 5.7213 | 5.7101 | 5.7434 | 5.7020 |
| 81 | 6.2955 | 6.3415 | 6.3262 | 6.3716 | 6.3153 |
| 82 | 7.0493 | 7.1137 | 7.0922 | 7.1561 | 7.0770 |
| 83 | 8.0067 | 8.1006 | 8.0691 | 8.1630 | 8.0471 |
| 84 | 9.2609 | 9.4047 | 9.3564 | 9.5017 | 9.3226 |
| 85 | 10.970 | 11.205 | 11.126 | 11.367 | 11.071 |
| 86 | 13.426 | 13.846 | 13.703 | 14.146 | 13.605 |
| 87 | 17.223 | 18.075 | 17.780 | 18.720 | 17.584 |
3.4. A Diamond Dust Case at Dome C from National Institute of Optics (INO), National Council of Research (CNR) Antarctic Lidar Measurements

3.5. Various Tropospheric Cirrus Cloud Cases from Lidar Measurements at Ny-Ålesund and Thule

| θ (°) | Thin Cirrus Clouds at Ny-Ålesund | Thin Cirrus Clouds at Thule | Ratios mcc(θ)/ma(θ) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Case (a), 11 April 2013 | Case (b), 12 July 2013 | Case (c), 15 October 2013 | Case (d), 12 June 2012 | Case (e), 30 January 2014 | Case (a) | Case (b) | Case (c) | Case (d) | Case (e) | |
| 0 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 10 | 1.0154 | 1.0154 | 1.0154 | 1.0154 | 1.0154 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 20 | 1.0640 | 1.0641 | 1.0641 | 1.0640 | 1.0640 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 30 | 1.1543 | 1.1545 | 1.1545 | 1.1543 | 1.1543 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 40 | 1.3044 | 1.3049 | 1.3049 | 1.3045 | 1.3045 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 50 | 1.5533 | 1.5545 | 1.5544 | 1.5535 | 1.5534 | 0.999 | 1.000 | 1.000 | 0.999 | 0.999 |
| 55 | 1.7395 | 1.7415 | 1.7413 | 1.7399 | 1.7398 | 0.999 | 1.000 | 1.000 | 0.999 | 0.999 |
| 60 | 1.9933 | 1.9968 | 1.9964 | 1.9941 | 1.9938 | 0.998 | 1.000 | 1.000 | 0.999 | 0.998 |
| 65 | 2.3541 | 2.3604 | 2.3597 | 2.3555 | 2.3550 | 0.997 | 1.000 | 0.999 | 0.998 | 0.997 |
| 70 | 2.8995 | 2.9121 | 2.9106 | 2.9022 | 2.9013 | 0.995 | 1.000 | 0.999 | 0.996 | 0.996 |
| 72 | 3.2024 | 3.2199 | 3.2178 | 3.2061 | 3.2050 | 0.994 | 1.000 | 0.999 | 0.996 | 0.995 |
| 74 | 3.5797 | 3.6047 | 3.6018 | 3.5850 | 3.5834 | 0.993 | 1.000 | 0.999 | 0.994 | 0.993 |
| 75 | 3.8051 | 3.8355 | 3.8319 | 3.8115 | 3.8096 | 0.992 | 1.000 | 0.998 | 0.993 | 0.992 |
| 76 | 4.0614 | 4.0988 | 4.0944 | 4.0694 | 4.0671 | 0.990 | 1.000 | 0.998 | 0.992 | 0.991 |
| 77 | 4.3554 | 4.4020 | 4.3966 | 4.3653 | 4.3625 | 0.989 | 1.000 | 0.998 | 0.991 | 0.990 |
| 78 | 4.6955 | 4.7545 | 4.7478 | 4.7081 | 4.7046 | 0.987 | 0.999 | 0.997 | 0.990 | 0.988 |
| 79 | 5.0932 | 5.1694 | 5.1608 | 5.1095 | 5.1052 | 0.984 | 0.999 | 0.997 | 0.988 | 0.986 |
| 80 | 5.5636 | 5.6641 | 5.6529 | 5.5852 | 5.5798 | 0.981 | 0.999 | 0.996 | 0.985 | 0.983 |
| 81 | 6.1276 | 6.2636 | 6.2487 | 6.1570 | 6.1501 | 0.977 | 0.999 | 0.995 | 0.982 | 0.979 |
| 82 | 6.8142 | 7.0039 | 6.9837 | 6.8554 | 6.8467 | 0.971 | 0.998 | 0.994 | 0.977 | 0.974 |
| 83 | 7.6648 | 7.9395 | 7.9113 | 7.7249 | 7.7140 | 0.962 | 0.997 | 0.992 | 0.970 | 0.966 |
| 84 | 8.7394 | 9.1559 | 9.1153 | 8.8315 | 8.8186 | 0.950 | 0.996 | 0.990 | 0.961 | 0.956 |
| 85 | 10.126 | 10.794 | 10.734 | 10.276 | 10.264 | 0.932 | 0.994 | 0.985 | 0.946 | 0.940 |
| 86 | 11.954 | 13.102 | 13.014 | 12.217 | 12.218 | 0.902 | 0.989 | 0.977 | 0.922 | 0.915 |
| 87 | 14.401 | 16.551 | 16.432 | 14.910 | 14.980 | 0.851 | 0.977 | 0.963 | 0.880 | 0.873 |
4. Conclusions
Acknowledgments
Author Contributions
List of symbols
| α | Ångström (1964) exponent derived from spectral series of τa(λ) over the visible and near-infrared wavelength range |
| θ | apparent solar zenith angle |
| τ(λ) | total optical thickness of the atmosphere at wavelength λ |
| τa(λ) | aerosol optical thickness at wavelength λ |
| τa(0.532 μm) | aerosol optical thickness derived from lidar measurements at wavelength λ = 0.532 μm |
| τbaa(0.532 μm) | optical thickness derived from lidar measurements for summer background Arctic aerosols |
| τbAa(0.532 μm) | optical thickness derived from lidar measurements for austral summer background Antarctic aerosols |
| τcc(0.532 μm) | optical thickness derived from lidar measurements for cirrus cloud particles |
| τdd(0.532 μm) | optical thickness derived from lidar measurements for diamond dust at the Antarctic high-altitude sites |
| τj(λ) | optical thickness produced at wavelength λ by absorption of the j-th atmospheric gaseous constituent |
| τR(λ) | rayleigh scattering optical thickness at wavelength λ |
| Bbs(0.532 μm) | volume backscattering coefficient measured by the lidar-systems employed at Ny-Ålesund (Spitsbergen, Svalbard), onboard the CALIOP/CALIPSO satellite, at Thule (north-western Greenland) and Dome C (Antarctic Plateau) |
| D | correction factor used in the Bouguer-Lambert-Beer law applied to the Sun-photometry method to take into account the day-to-day variations in the direct solar irradiance associated with the Earth-Sun distance changes |
| e(z) | water vapor partial pressure at altitude z |
| J(λ) | ground-level direct solar irradiance at wavelength λ |
| Jo(λ) | extra-terrestrial output voltage of the sun-photometer at wavelength λ |
| Ka | integral of ka(z) made over the zo ≤ z ≤ z∞ altitude range |
| ka(0.532 μm) | aerosol volume extinction coefficient derived from lidar measurements |
| ka(z) | aerosol volume extinction coefficient at altitude z |
| m(θ), m | relative optical air mass of the atmosphere for a certain solar zenith angle θ |
| ma(θ), ma | relative optical air mass for aerosol extinction at solar zenith angle θ |
| mbaa(θ) | relative optical air mass calculated at solar zenith angle θ for summer background Arctic aerosols |
| mbAa(θ) | relative optical air mass calculated at solar zenith angle θ for austral summer background Antarctic aerosols |
| mcc(θ) | relative optical air mass calculated at solar zenith angle θ for cirrus cloud particles |
| mdd(θ) | relative optical air mass calculated at solar zenith angle θ for diamond dust at Antarctic high-altitude sites |
| mj | relative optical air mass for the j-th atmospheric gaseous constituent |
| n(z) | air refractive index at altitude z |
| no | refractive index of air at the sea-level |
| p(z) | air pressure at altitude z; |
| T(z) | air temperature at altitude z |
| V0 | ground-level visual range defined in the well-known Koschmieder [36] formula |
| λ | wavelength (usually measured in μm) |
| z | altitude measured above the mean sea-level |
| z∞ | atmospheric top-level |
| zo | mean sea-level |
Conflicts of Interest
References
- Tomasi, C.; Kokhanovsky, A.A.; Lupi, A.; Ritter, C.; Smirnov, A.; O’Neill, N.T.; Stone, R.S.; Holben, B.N.; Nyeki, S.; Wehrli, C.; Stohl, A.; et al. Aerosol remote sensing in polar regions. Earth-Sci. Rev. 2015, 140, 108–157. [Google Scholar] [CrossRef] [Green Version]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanré, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Nakajima, T.; Yoon, S.C.; Ramanathan, V.; Shi, G.Y.; Takemura, T.; Higurashi, A.; Takamura, T.; Aoki, K.; Sohn, B.J.; Kim, S.W.; et al. Overview of the atmospheric brown cloud East Asian regional experiment 2005 and a study of the aerosol direct radiative forcing in East Asia. J. Geophys. Res. 2007, 112, D24S91. [Google Scholar]
- Smirnov, A.; Holben, B.N.; Slutsker, I.; Giles, D.M.; McClain, C.R.; Eck, T.F.; Sakerin, S.M.; Macke, A.; Croot, P.; Zibordi, G.; et al. Maritime Aerosol Network as a component of Aerosol Robotic Network. J. Geophys. Res. 2009, 114, D06204. [Google Scholar]
- Ohno, T. Aerosol routine observation operated by the Japan Meteorological Agency. In Proceedings of WMO/GAW Experts Workshop on a Global Surface-Based Network for Long Term Observations of Column Aerosol Optical Properties, Davos, Switzerland, 8–10 March 2004; pp. 70–71.
- Tomasi, C.; Vitale, V.; Lupi, A.; Di Carmine, C.; Campanelli, M.; Herber, A.; Treffeisen, R.; Stone, R.S.; Andrews, E.; Sharma, S.; et al. Aerosols in polar regions: A historical overview based on optical depth and in situ observations. J. Geophys. Res. 2007, 112, D16205. [Google Scholar]
- Tomasi, C.; Lupi, A.; Mazzola, M.; Stone, R.S.; Dutton, E.G.; Herber, A.; Vitale, V.; Radionov, V.F.; Holben, B.N.; Sorokin, M.G.; et al. An update of the long-term aerosol optical properties in polar regions using POLAR-AOD and other measurements performed during the International Polar Year. Atmos. Environ. 2012, 52, 29–47. [Google Scholar] [CrossRef] [Green Version]
- Wehrli, C. Calibrations of filter radiometers for determination of atmospheric optical depths. Metrologia 2000, 37, 419–422. [Google Scholar] [CrossRef]
- Stone, R.S. Monitoring aerosol optical depth at Barrow, Alaska, and South Pole; Historical overview, recent results and future goals. SIF Conf. Proc. 2002, 80, 123–144. [Google Scholar]
- Shiobara, M.; Yamano, M.; Kobayashi, H.; Aoki, K.; Yabuki, M. Sky-radiometer measurement for monitoring column aerosol optical properties in Ny-Alesund—Recent results from the spring 2006–2007 measurements. In Proceedings of 8th Ny-Alesund Seminar, Cambridge, UK, 16–17 October 2007; pp. 32–35.
- Di Carmine, C.; Campanelli, M.; Nakajima, T.; Tomasi, C.; Vitale, V. Retrievals of Antarctic aerosol characteristics using a Sun-sky radiometer during the 2001–2002 austral summer campaign. J. Geophys. Res. 2005, 110, D13202. [Google Scholar] [CrossRef]
- Herber, A.; Thomason, L.W.; Gernandt, H.; Leiterer, U.; Nagel, D.; Schulz, K.-H.; Kaptur, J.; Albrecht, T.; Notholt, J. Continuous day and night aerosol optical depth observations in the Arctic between 1991 and 1999. J. Geophys. Res. 2002. [Google Scholar] [CrossRef]
- Leiterer, U.; Weller, M. Sunphotometer BAS and ABAS for atmospheric research. WMO Tech. Doc. 1988, 222, 21–26. [Google Scholar]
- Radionov, V.F.; Lamakin, M.V.; Herber, A. Changes in the aerosol optical depth of the Antarctic atmosphere. Izv. Atmos. Ocean. Phys. 2002, 38, 179–183. [Google Scholar]
- Sakerin, S.M.; Kabanov, D.M.; Rostov, A.P.; Turchinovich, S.A. Portative solar photometer. Prib. Tekhnika Eksp. (Instrum. Exp. Tech.). 2009, 2, 181–182. (In Russian) [Google Scholar]
- Tomasi, C.; Prodi, F.; Sentimenti, M.; Cesari, G. Multiwavelength sun-photometers for accurate measurements of atmospheric extinction in the visible and near-IR spectral range. Appl. Opt. 1983, 22, 622–630. [Google Scholar] [CrossRef] [PubMed]
- Tomasi, C.; Vitale, V.; Tagliazucca, M. Atmospheric turbidity measurements at Terra Nova Bay during January and February 1988. SIF Conf. Proc. 1989, 20, 67–77. [Google Scholar]
- Shaw, G.E. Error analysis of multi-wavelength sun photometry. Pure Appl. Geophys. 1976, 114, 1–14. [Google Scholar] [CrossRef]
- Iqbal, M. An Introduction to Solar Radiation; Academic Press: Toronto, ON, Canada, 1983; p. 390. [Google Scholar]
- Mazzola, M.; Stone, R.S.; Herber, A.; Tomasi, C.; Lupi, A.; Vitale, V.; Lanconelli, C.; Toledano, C.; Cachorro, V.E.; O’Neill, N.T.; et al. Evaluation of sun-photometer capabilities for retrievals of aerosol optical depth at high latitudes: The POLAR-AOD intercomparison campaigns. Atmos. Environ. 2012, 52, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Di Biagio, C.; Di Sarra, A.; Eriksen, P.; Ascanius, S.E.; Muscari, G.; Holben, B. Effect of surface albedo, water vapour, and atmospheric aerosols on the cloud-free shortwave radiative budget in the Arctic. Clim. Dyn. 2012, 39, 953–969. [Google Scholar] [CrossRef]
- Tomasi, C.; Petkov, B.H. Calculations of relative optical air masses for various aerosol types and minor gases in Arctic and Antarctic atmospheres. J. Geophys. Res.: Atmos. 2014, 119, 1363–1385. [Google Scholar] [CrossRef]
- Tomasi, C.; Vitale, V.; Petkov, B.; Lupi, A.; Cacciari, A. Improved algorithm for calculations of Rayleigh-scattering optical depth in standard atmospheres. Appl. Opt. 2005, 44, 3320–3341. [Google Scholar] [CrossRef] [PubMed]
- Tomasi, C.; Petkov, B.; Stone, R.S.; Benedetti, E.; Vitale, V.; Lupi, A.; Mazzola, M.; Lanconelli, C.; Herber, A.; von Hoyningen-Huene, W. Characterizing polar atmospheres and their effect on Rayleigh-scattering optical depth. J. Geophys. Res. 2010, 115, D02205. [Google Scholar] [CrossRef]
- Tomasi, C.; Cacciari, A.; Vitale, V.; Lupi, A.; Lanconelli, C.; Pellegrini, A.; Grigioni, P. Mean vertical profiles of temperature and absolute humidity from a twelve-year radiosounding data-set at Terra Nova Bay (Antarctica). Atmos. Res. 2004, 71, 139–169. [Google Scholar] [CrossRef]
- Kneizys, F.X.; Abreu, L.W.; Anderson, G.P.; Chetwind, J.H.; Shettle, E.P.; Berk, A.; Bernstein, L.S.; Robertson, D.C.; Acharya, P.; Rothman, L.S.; et al. The MODTRAN 2/3 Report and LOWTRAN 7 Model; Abreu, L.W., Anderson, G.P., Eds.; Ontar Corporation: North Andover, MA, USA, 1996; p. 261. [Google Scholar]
- Anderson, G.P.; Clough, S.A.; Kneizys, F.X.; Chetwind, J.H.; Shettle, E.P. AFGL Atmospheric Constituent Profiles (0–120 km); U.S. Air Force Geophysics Laboratory: Bedford, MA, USA, 1986; p. 43.
- Michalsky, J.; Beauharnois, M.; Berndt, J.; Harrison, L.; Kiedron, P.; Min, Q. O2-O2 absorption band identification based on optical depth spectra of the visible and near-infrared. Geophys. Res. Lett. 1999, 26, 1581–1584. [Google Scholar] [CrossRef]
- Hoffmann, A.; Ritter, C.; Stock, M.; Maturilli, M.; Eckhardt, S.; Herber, A.; Neuber, R. Lidar measurements of the Kasatochi aerosol plume in August and September 2008 in Ny-Ålesund, Spitsbergen. J. Geophys. Res. 2010, 115, D00L12. [Google Scholar] [CrossRef]
- Thomason, L.W.; Herman, B.M.; Reagan, J.A. The effect of atmospheric attenuators with structured vertical distributions on air mass determinations and Langley plot analyses. J. Atmos. Sci. 1983, 40, 1851–1854. [Google Scholar] [CrossRef]
- Tomasi, C.; Petkov, B.; Benedetti, E.; Valenziano, L.; Vitale, V. Analysis of a 4 year radiosonde data set at Dome C for characterizing temperature and moisture conditions of the Antarctic atmosphere. J. Geophys. Res. 2011, 116, D15304. [Google Scholar]
- Ansmann, A.; Wandinger, U.; Riebesell, M.; Weitkamp, C.; Michaelis, W. Independent measurement of extinction and backscatter profiles in cirrus clouds by using a combined Raman elastic-backscatter LiDAR. Appl. Opt. 1992, 31, 7113–7131. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, A.; Ritter, C.; Stock, M.; Shiobara, M.; Lampert, A.; Maturilli, M.; Orgis, T.; Neuber, R.; Herber, A. Ground-based lidar measurements from Ny-Ålesund during ASTAR 2007. Atmos. Chem. Phys. 2009, 9, 9059–9081. [Google Scholar] [CrossRef]
- Kim, S.-W.; Berthier, S.; Raut, J.-C.; Chazette, P.; Dulac, F.; Yoon, S.-C. Validation of aerosol and cloud layer structures from the space-borne LiDAR CALIOP using a ground-based lidar in Seoul, Korea. Atmos. Chem. Phys. 2008, 8, 3705–3720. [Google Scholar] [CrossRef]
- Muscari, G.; Di Biagio, C.; Di Sarra, A.; Cacciani, M.; Ascanius, S.E.; Bertagnolio, P.P.; Cesaroni, C.; de Zafra, R.L.; Eriksen, P.; Fiocco, G.; et al. Observations of surface radiative budget and stratospheric processes at Thule Air Base, Greenland. Ann. Geophys. 2014, 57, 1–14. [Google Scholar]
- Koschmieder, H. Theorie der horizontalen Sichtweite. Beitr. Phys. Atmos. 1925, 12, 33–53, 171–181. [Google Scholar]
- Ångström, A. The parameters of atmospheric turbidity. Tellus 1964, 16, 64–75. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomasi, C.; Petkov, B.H.; Mazzola, M.; Ritter, C.; Di Sarra, A.G.; Di Iorio, T.; Del Guasta, M. Seasonal Variations of the Relative Optical Air Mass Function for Background Aerosol and Thin Cirrus Clouds at Arctic and Antarctic Sites. Remote Sens. 2015, 7, 7157-7180. https://doi.org/10.3390/rs70607157
Tomasi C, Petkov BH, Mazzola M, Ritter C, Di Sarra AG, Di Iorio T, Del Guasta M. Seasonal Variations of the Relative Optical Air Mass Function for Background Aerosol and Thin Cirrus Clouds at Arctic and Antarctic Sites. Remote Sensing. 2015; 7(6):7157-7180. https://doi.org/10.3390/rs70607157
Chicago/Turabian StyleTomasi, Claudio, Boyan H. Petkov, Mauro Mazzola, Christoph Ritter, Alcide G. Di Sarra, Tatiana Di Iorio, and Massimo Del Guasta. 2015. "Seasonal Variations of the Relative Optical Air Mass Function for Background Aerosol and Thin Cirrus Clouds at Arctic and Antarctic Sites" Remote Sensing 7, no. 6: 7157-7180. https://doi.org/10.3390/rs70607157
APA StyleTomasi, C., Petkov, B. H., Mazzola, M., Ritter, C., Di Sarra, A. G., Di Iorio, T., & Del Guasta, M. (2015). Seasonal Variations of the Relative Optical Air Mass Function for Background Aerosol and Thin Cirrus Clouds at Arctic and Antarctic Sites. Remote Sensing, 7(6), 7157-7180. https://doi.org/10.3390/rs70607157