Validation and Performance Evaluations of Methods for Estimating Land Surface Temperatures from ASTER Data in the Middle Reach of the Heihe River Basin, Northwest China
Abstract
:1. Introduction
2. Study Area and Datasets
2.1. Study Area and in situ LST Measurements

| Name | Four-Component Radiometer Set | Land Cover Type | ||
|---|---|---|---|---|
| Instrument | Height (m) | Diameter of FOV (m) | ||
| >EC01 | CNR1 | 6.0 | 44.78 | Vegetable |
| EC02 | CNR4 | 4.0 | 29.86 | Maize |
| EC03 | NR01 | 6.0 | 44.78 | Maize |
| EC04 | CNR1 | 6.0 | 44.78 | Residential areas |
| EC05 | CNR1 | 4.0 | 29.86 | Maize |
| EC06 | CNR4 | 6.0 | 44.78 | Maize |
| EC07 | CNR4 | 4.0 | 29.86 | Maize |
| EC08 | CNR4 | 6.0 | 44.78 | Maize |
| EC09 | CNR1 | 6.0 | 44.78 | Maize |
| EC10 | CNR1 | 6.0 | 44.78 | Maize |
| EC11 | CNR1 | 4.0 | 29.86 | Maize |
| EC12 | CNR4 | 4.0 | 29.86 | Maize |
| EC13 | CNR4 | 5.5 | 41.05 | Maize |
| EC14 | CNR4 | 6.0 | 44.78 | Maize |
| EC15 | PSP and PIR | 12.0 | 89.57 | Maize |
| EC17 | CNR1 | 6.0 | 44.78 | Apple orchard |
| SD | NR01 | 6.0 | 44.78 | Wetland |
| GB | CNR1 | 6.0 | 44.78 | Gobi |
| SSW | NR01 | 6.0 | 44.78 | Sandy desert |
2.2. Remote Sensing Datasets

2.3. Atmospheric Profiles
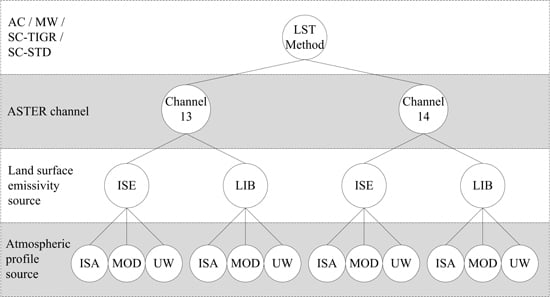
3. Methodology
3.1. Methods for Estimating LSTs
3.1.1. The Atmospheric Correction (AC) Method
3.1.2. The Mono-Window (MW) Method
| Channel | a | b | R2 | F Test | Standard Error of Estimation |
|---|---|---|---|---|---|
| 13 | 0.4404 | −66.0506 | 0.9995 | 128467.9511 | 0.1690 |
| 14 | 0.4620 | −68.8317 | 0.9996 | 136422.0490 | 0.1720 |
3.1.3. The Single-Channel (SC) Method
3.1.4. The Split-Window (SW) Method
3.2. Determining the Input Parameters for Each Method
3.3. Validation and Performance Evaluations of the LST Methods
3.3.1. The Actual ASTER Dataset

3.3.2. The Simulation Dataset
4. Results
4.1. Characterizing the Surface Homogeneity of the Ground Sites


4.2. Evaluation with the in Situ Measured LSTs
4.2.1. Implementing Methods with in situ Measured LSEs and Atmospheric Parameters

| Method | Bias and RMSE with Derived WVC and τ from the Atmospheric Profile (K) | Bias and RMSE with Estimated WVC and τ (K) | ||||
|---|---|---|---|---|---|---|
| Homogenous Samples | All Samples | Homogenous Samples | All Samples | |||
| All | Oasis | All | Oasis | |||
| AC-13-ISE-ISA | 0.65 / 2.14 | 0.73 / 1.49 | 0.58 / 2.54 | -- | -- | -- |
| AC-14-ISE-ISA | 0.63 / 2.21 | 0.73 / 1.55 | 0.55 / 2.65 | -- | -- | -- |
| MW-13-ISE-ISA | 0.05 / 2.31 | 0.11 / 1.56 | 0.0 / 2.67 | 0.09 / 2.39 | 0.13 / 1.63 | 0.02 / 2.73 |
| MW-14-ISE-ISA | −0.06 / 2.49 | 0.03 / 1.77 | −0.13 / 2.88 | 0.0 / 2.57 | 0.06 / 1.84 | −0.10 / 2.96 |
| SC-STD-13-ISE-ISA | 1.97 / 2.73 | 2.05 / 2.32 | 1.94 / 3.12 | 2.09 / 3.05 | 2.11 / 2.47 | 1.99 / 3.24 |
| SC-STD-14-ISE-ISA | 2.14 / 2.89 | 2.25 / 2.51 | 2.10 / 3.29 | 2.32 / 3.35 | 2.33 / 2.76 | 2.17 / 3.52 |
| SC-TIGR-13-ISE-ISA | 1.79 / 2.60 | 1.87 / 2.17 | 1.74 / 2.97 | 1.92 / 2.87 | 1.95 / 2.32 | 1.80 / 3.09 |
| SC-TIGR-14-ISE-ISA | 2.06 / 2.82 | 2.17 / 2.44 | 1.99 / 3.20 | 2.24 / 3.22 | 2.27 / 2.69 | 2.08 / 3.41 |
| SW-WE-ISE-ISA | 0.01 / 2.03 | 0.10 / 1.68 | −0.06 / 2.46 | 0.02 / 2.02 | 0.12 / 1.67 | −0.05 / 2.45 |
4.2.2. Implementing Methods with in Situ Measured LSEs and Alternative Atmospheric Parameters
4.2.3. Implementing Methods with Alternative LSEs and in Situ Measured Atmospheric Parameters
| Method | Bias and RMSE with Derived WVC and τ from the Atmospheric Profile (K) | Bias and RMSE with Estimated WVC and τ (K) | ||||
|---|---|---|---|---|---|---|
| Homogenous Samples | All Samples | Homogenous Samples | All Samples | |||
| All | Oasis | All | Oasis | |||
| AC-13-ISE-MOD | 2.18 / 3.03 | 2.24 / 2.66 | 2.14 / 3.39 | -- | -- | -- |
| AC-14-ISE-MOD | 2.61 / 3.48 | 2.68 / 3.16 | 2.55 / 3.82 | -- | -- | -- |
| MW-13-ISE-MOD | 0.10 / 2.29 | 0.15 / 1.46 | 0.09 / 2.68 | −0.11 / 2.22 | 0.0 / 1.56 | −0.20 / 2.57 |
| MW-14-ISE-MOD | 0.02 / 2.49 | 0.09 / 1.65 | 0.0 / 2.87 | −0.23 / 2.39 | −0.10 / 1.75 | −0.36 / 2.77 |
| SC-STD-13-ISE-MOD | 2.30 / 3.08 | 2.35 / 2.66 | 2.31 / 3.53 | 1.67 / 2.43 | 1.80 / 2.08 | 1.59 / 2.81 |
| SC-STD-14-ISE-MOD | 2.60 / 3.39 | 2.67 / 3.01 | 2.63 / 3.89 | 1.77 / 2.51 | 1.93 / 2.21 | 1.67 / 2.93 |
| SC-TIGR-13-ISE-MOD | 2.04 / 2.87 | 2.10 / 2.43 | 2.03 / 3.27 | 1.52 / 2.33 | 1.64 / 1.96 | 1.42 / 2.70 |
| SC-TIGR-14-ISE-MOD | 2.40 / 3.20 | 2.48 / 2.82 | 2.39 / 3.62 | 1.73 / 2.49 | 1.89 / 2.17 | 1.60 / 2.86 |
| SW-WE-ISE-MOD | 0.03 / 2.03 | 0.12 / 1.68 | -0.05 / 2.46 | −0.01 / 2.03 | 0.08 / 1.69 | −0.09 / 2.47 |
| AC-13-ISE-UW | 0.95 / 2.15 | 1.06 / 1.62 | 0.87 / 2.54 | -- | -- | -- |
| AC-14-ISE-UW | 1.01 / 2.22 | 1.15 / 1.71 | 0.91 / 2.64 | -- | -- | -- |
| MW-13-ISE-UW | −0.09 / 2.26 | 0.0 / 1.57 | −0.16 / 2.62 | 0.37 / 2.58 | 0.38 / 1.72 | 0.32 / 2.81 |
| MW-14-ISE-UW | −0.21 / 2.44 | −0.09 / 1.77 | −0.30 / 2.83 | 0.33 / 2.81 | 0.34 / 1.94 | 0.25 / 3.05 |
| SC-STD-13-ISE-UW | 1.68 / 2.49 | 1.79 / 2.13 | 1.61 / 2.87 | 2.98 / 4.02 | 2.90 / 3.31 | 2.91 / 4.15 |
| SC-STD-14-ISE-UW | 1.79 / 2.60 | 1.94 / 2.28 | 1.70 / 3.01 | 3.51 / 4.76 | 3.40 / 3.95 | 3.42 / 4.85 |
| SC-TIGR-13-ISE-UW | 1.51 / 2.38 | 1.62 / 1.99 | 1.43 / 2.76 | 2.68 / 3.67 | 2.64 / 3.03 | 2.60 / 3.81 |
| SC-TIGR-14-ISE-UW | 1.72 / 2.56 | 1.87 / 2.22 | 1.61 / 2.94 | 3.25 / 4.34 | 3.19 / 3.65 | 3.14 / 4.43 |
| SW-WE-ISE-UW | −0.02 / 2.03 | 0.07 / 1.68 | −0.09 / 2.46 | 0.09 / 1.99 | 0.19 / 1.66 | 0.01 / 2.43 |
| Method | Bias and RMSE with Derived WVC and τ from the Atmospheric Profile (K) | Bias and RMSE with Estimated WVC and τ (K) | ||||
|---|---|---|---|---|---|---|
| Homogenous Samples | All Samples | Homogenous Samples | All Samples | |||
| All | Oasis | All | Oasis | |||
| AC-13-LIB-ISA | 0.59 / 2.08 | 0.71 / 1.51 | 0.55 / 2.56 | -- | -- | -- |
| AC-14-LIB-ISA | 0.13 / 2.11 | 0.25 / 1.43 | 0.08 / 2.63 | -- | -- | -- |
| MW-13-LIB-ISA | −0.01 / 2.25 | 0.09 / 1.60 | −0.03 / 2.69 | 0.03 / 2.33 | 0.12 / 1.66 | −0.02 / 2.76 |
| MW-14-LIB-ISA | −0.61 / 2.55 | −0.51 / 1.87 | −0.65 / 2.98 | −0.55 / 2.62 | −0.47 / 1.93 | −0.62 / 3.05 |
| SC-STD-13-LIB-ISA | 1.91 / 2.65 | 2.03 / 2.32 | 1.90 / 3.11 | 2.04 / 2.96 | 2.09 / 2.47 | 1.95 / 3.22 |
| SC-STD-14-LIB-ISA | 1.61 / 2.51 | 1.73 / 2.08 | 1.60 / 3.02 | 1.79 / 3.00 | 1.82 / 2.36 | 1.68 / 3.25 |
| SC-TIGR-13-LIB-ISA | 1.73 / 2.52 | 1.85 / 2.17 | 1.70 / 2.96 | 1.86 / 2.79 | 1.93 / 2.33 | 1.76 / 3.08 |
| SC-TIGR-14-LIB-ISA | 1.52 / 2.45 | 1.64 / 2.02 | 1.49 / 2.93 | 1.71 / 2.86 | 1.76 / 2.28 | 1.59 / 3.14 |
| SW-WE-LIB-ISA | 1.62 / 2.48 | 1.81 / 2.40 | 1.48 / 2.81 | 1.61 / 2.48 | 1.80 / 2.39 | 1.47 / 2.81 |
4.2.4. Implementing Methods with Alternative LSEs and Atmospheric Parameters
| Method | Bias and RMSE with Derived WVC and τ from the Atmospheric Profile (K) | Bias and RMSE with Estimated WVC and τ (K) | ||||
|---|---|---|---|---|---|---|
| Homogenous Samples | All Samples | Homogenous Samples | All Samples | |||
| All | Oasis | All | Oasis | |||
| AC-13-LIB-MOD | 2.13 / 2.95 | 2.23 / 2.65 | 2.10 / 3.35 | -- | -- | -- |
| AC-14-LIB-MOD | 2.09 / 3.12 | 2.18 / 2.77 | 2.07 / 3.53 | -- | -- | -- |
| MW-13-LIB-MOD | 0.04 / 2.22 | 0.13 / 1.49 | 0.06 / 2.67 | −0.16 / 2.18 | −0.02 / 1.58 | −0.24 / 2.60 |
| MW-14-LIB-MOD | −0.52 / 2.52 | −0.44 / 1.73 | −0.50 / 2.93 | −0.79 / 2.50 | −0.64 / 1.89 | −0.89 / 2.91 |
| SC-STD-13-LIB-MOD | 2.24 / 3.00 | 2.33 / 2.66 | 2.28 / 3.49 | 1.62 / 2.36 | 1.78 / 2.08 | 1.55 / 2.80 |
| SC-STD-14-LIB-MOD | 2.07 / 3.00 | 2.16 / 2.60 | 2.14 / 3.59 | 1.23 / 2.15 | 1.41 / 1.78 | 1.17 / 2.69 |
| SC-TIGR-13-LIB-MOD | 1.99 / 2.79 | 2.08 / 2.43 | 2.00 / 3.24 | 1.47 / 2.26 | 1.63 / 1.96 | 1.38 / 2.69 |
| SC-TIGR-14-LIB-MOD | 1.87 / 2.83 | 1.96 / 2.40 | 1.89 / 3.32 | 1.18 / 2.13 | 1.35 / 1.75 | 1.09 / 2.63 |
| SW-WE-LIB-MOD | 1.61 / 2.47 | 1.80 / 2.39 | 1.47 / 2.80 | 1.64 / 2.49 | 1.83 / 2.41 | 1.50 / 2.81 |
| AC-13-LIB-UW | 0.90 / 2.09 | 1.04 / 1.63 | 0.83 / 2.55 | -- | -- | -- |
| AC-14-LIB-UW | 0.49 / 2.04 | 0.64 / 1.47 | 0.42 / 2.55 | -- | -- | -- |
| MW-13-LIB-UW | −0.15 / 2.21 | −0.02 / 1.60 | −0.20 / 2.65 | 0.32 / 2.50 | 0.36 / 1.74 | 0.28 / 2.81 |
| MW-14-LIB-UW | −0.77 / 2.55 | −0.63 / 1.91 | −0.83 / 2.96 | −0.20 / 2.78 | −0.18 / 1.96 | −0.25 / 3.07 |
| SC-STD-13-LIB-UW | 1.62 / 2.42 | 1.77 / 2.13 | 1.57 / 2.87 | 2.93 / 3.93 | 2.89 / 3.31 | 2.88 / 4.10 |
| SC-STD-14-LIB-UW | 1.24 / 2.26 | 1.41 / 1.87 | 1.19 / 2.77 | 3.02 / 4.39 | 2.93 / 3.56 | 2.96 / 4.52 |
| SC-TIGR-13-LIB-UW | 1.45 / 2.31 | 1.60 / 1.99 | 1.39 / 2.76 | 2.63 / 3.58 | 2.62 / 3.02 | 2.57 / 3.76 |
| SC-TIGR-14-LIB-UW | 1.16 / 2.22 | 1.32 / 1.82 | 1.09 / 2.72 | 2.75 / 3.96 | 2.70 / 3.26 | 2.67 / 4.11 |
| SW-WE-LIB-UW | 1.65 / 2.50 | 1.83 / 2.42 | 1.50 / 2.82 | 1.56 / 2.45 | 1.75 / 2.36 | 1.42 / 2.79 |
4.3. Comparisons between ASTER LST Images



4.4. Evaluation with the Simulation Dataset
| Method | With derived WVC and τ from the Atmospheric Profile (K) | With Estimated WVC and τ (K) | ||
|---|---|---|---|---|
| Bias | RMSE | Bias (K) | RMSE | |
| AC-13 | 0.0 | 0.08 | -- | -- |
| AC-14 | 0.0 | 0.10 | -- | -- |
| MW-13 | −0.77 | 0.84 | −0.73 | 0.95 |
| MW-14 | −0.95 | 1.02 | −0.90 | 1.15 |
| SC-STD-13 | 1.25 | 1.26 | 1.20 | 1.33 |
| SC-STD-14 | 1.41 | 1.43 | 1.33 | 1.56 |
| SC-TIGR-13 | 1.02 | 1.03 | 1.00 | 1.15 |
| SC-TIGR-14 | 1.27 | 1.28 | 1.23 | 1.45 |
| SW-WE | −1.06 | 1.37 | −1.06 | 1.37 |

5. Discussion
6. Conclusions
Acknowledgements
Author Contributions
Acronyms
| AC | atmospheric correction |
| AMS | Automatic Meteorological Station |
| HiWATER | Heihe Watershed Allied Telemetry Experimental Research |
| HRB | Heihe River basin |
| ISA | in situ measured atmospheric profile |
| ISE | in situ measured land surface emissivity |
| LIB | land surface emissivity determined based on the MODIS UCSB Emissivity Library |
| LSE | land surface emissivity |
| LST | land surface temperature |
| MOD | MOD07_L2 product |
| MUSOEXE | Multi-Scale Observation Experiment on Evapotranspiration |
| MW | mono-window |
| NDVI | normalized difference vegetation index |
| SC | single-channel |
| STD | standard atmospheric profiles in MODTRAN code |
| SW | split-window |
| SW-QUAD | split-window method without the water vapor content and land surface emissivity as the inputs |
| SW-WE | split-window method with the water vapor content and land surface emissivity as the inputs |
| TIGR | Thermodynamic Initial Guess Retrieval (TIGR) |
| TIR | thermal infrared |
| UW | University of Wyoming |
| WVC | water vapor content |
Conflicts of Interest
References
- Ma, Y.; Liu, S.; Zhang, F.; Zhou, J.; Jia, Z.; Song, L. Estimations of regional surface energy fluxes over heterogeneous oasis–desert surfaces in the middle reaches of the Heihe River during HiWATER-MUSOEXE. IEEE Geosci. Remote Sens. Lett. 2015, 12, 671–675. [Google Scholar] [CrossRef]
- Berk, A.; Bernstein, L.S.; Anderson, G.P.; Acharya, P.K.; Robertson, D.C. MODTRAN cloud and multiple scattering upgrades wit application to AVIRIS. Remote Sens. Environ. 1998, 65, 367–375. [Google Scholar]
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Kharraz, J.E.L. Surface temperature and water vapour retrieval from MODIS data. Int. J. Remote Sens 2003, 24, 5161–5182. [Google Scholar]
- Yu, Y.; Privette, J.L.; Pinheiro, A.C. Evaluation of split-window land surface temperature algorithms for generating climate data records. IEEE Trans. Geosci. Remote Sens. 2008, 46, 179–192. [Google Scholar] [CrossRef]
- Yu, Y.; Tarpley, D.; Privette, J.; Goldberg, M.D.; Varma Raja, M.K.R.; Vinnikov, K.Y.; Xu, H. Developing algorithm for operational GOES-R land surface temperature product. IEEE Trans. Geosci. Remote Sens. 2009, 47, 936–951. [Google Scholar]
- Guillevic, P.C.; Biard, J.C.; Hulley, G.C.; Privette, J.L.; Hook, S.J.; Olioso, A.; Göttsche, F.M.; Radocinski, R.; Román, M.O.; Yu, Y.; et al. Validation of land surface temperature products derived from the Visible Infrared Imaging Radiometer Suite (VIIRS) using ground-based and heritage satellite measurements. Remote Sens. Environ. 2014, 154, 19–37. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Paolini, L. Land surface temperature retrieval from Landsat TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Zhou, J.; Li, J.; Zhang, L.; Hu, D.; Zhan, W. Intercomparison of methods for estimating land surface temperature from a Landsat-5 TM image in an arid region with low water vapour in the atmosphere. Int. J. Remote Sens. 2012, 33, 2582–2602. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Anne, B.; Kahle, H.T. Overview of Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER). IEEE Trans. Geosci. Remote Sens. 1998, 36, 1062–1071. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Rem. Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Wang, K.; Liang, S. Evaluation of ASTER and MODIS land surface temperature and emissivity products using long-term surface longwave radiation observations at SURFRAD sites. Remote Sens. Environ. 2009, 113, 1556–1565. [Google Scholar] [CrossRef]
- Pu, R.; Gong, P.; Michishita, R.; Sasagawa, T. Assessment of multi-resolution and multi-sensor data for urban surface temperature retrieval. Remote Sens. Environ. 2006, 104, 211–225. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C. , Sobrino, J.A. Feasibility of retrieving land-surface temperature from ASTER TIR bands using two-channel algorithms: A case study of agricultural areas. IEEE Geosci. Remote Sens. 2007, 4, 60–64. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Sobrino, J.A. A single-channel algorithm for land-surface temperature retrieval from ASTER data. IEEE Geosci. Remote Sens. 2010, 4, 60–64. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y.; et al. Heihe watershed allied telemetry experimental research (HiWATER): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, S.; Li, X.; Shi, S.; Wang, J.; Zhu, Z.; Xu, T.; Wang, W.; Ma, M. Intercomparison of surface energy flux measurement systems used during the HiWATER-MUSOEXE. J. Geophys. Res. 2013, 118, 13140–13157. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Wang, W.; Bai, J.; Jia, Z.; Zhu, M.; Wang, J. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sc. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]
- Yan, K.; Ren, H.; Hu, R.; Mu, X.; Liu, Z.; Yan, G. Error analysis for emissivity measurement using FTIR spectrometer. In Proceedings of IEEE International Geoscience and Remote Sensing Symposium, Melbourne, VIC, Australia, 21–26 July 2013; pp. 3080–3083.
- Mu, X.; Hu, R.; Huang, S.; Chen, Y. HiWATER: Dataset of Emissivity in the Middle Reaches of the Heihe River Basin in 2012; Cold and Arid Regions Science Data Center at Lanzhou: Lanzhou, China, 2012. [Google Scholar]
- Berry, T.E.; Melton, R.E. Multi-spectral thermal image analysis of natural backgrounds and targets. Proc. SPIE 2005, 5794, 866–874. [Google Scholar]
- Mu, X.; Huang, S.; Chen, Y. HiWATER: Dataset of Fractional Vegetation Cover in the Middle Reaches of the Heihe River Basin; Cold and Arid Regions Science Data Center at Lanzhou: Lanzhou, China, 2012. [Google Scholar]
- Liu, Y.; Mu, X.; Wang, H.; Yan, G. A novel method for extracting green fractional vegetation cover from digital images. J. Veg. Sci. 2012, 23, 406–418. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, X.; Zhan, W.; Zhang, H. Land surface temperature retrieval from MODIS data by integrating regression models and the genetic algorithm in an arid region. Remote Sens. 2014, 6, 5344–5367. [Google Scholar] [CrossRef]
- Xiao, Q.; Wen, J. HiWATER: Land Surface Temperature Product in the Middle Reaches of the Heihe River Basin (30th, June, 2012); Cold and Arid Regions Science Data Center at Lanzhou: Lanzhou, China, 2012. [Google Scholar]
- Xiao, Q.; Wen, J. HiWATER: Land Surface Temperature Product in the Middle Reaches of the Heihe River Basin (10th, July, 2012); Cold and Arid Regions Science Data Center at Lanzhou: Lanzhou, China, 2012. [Google Scholar]
- Wang, H.; Xiao, Q.; Li, H.; Zhong, B. Temperature and emissivity separation algorithm for TASI airborne thermal hyperspectral data. In Proceedings of IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1075–1078.
- TASI-600 Thermal Airborne Broadband Imager. Available online: http://www.itres.com/tasi-600/ (accessed on 19 April 2015).
- Tan, J.; Ma, M. HiWATER: Dataset of Radiosonde Sounding Observations in Zhangye National Climate Observatory; Cold and Arid Regions Science Data Center at Lanzhou: Lanzhou, China, 2012. [Google Scholar]
- Ottlé, C.; Stoll, M. Effect of atmospheric absorption and surface emissivity on the determination of land surface temperature from infrared satellite data. Int. J. Rem. Sens. 1993, 14, 2025–2037. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. Int. J. Remote Sens. 2001, 22, 3719–3746. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Sobrino, J.A. A generalized single-channel method for retrieving land surface temperature from remote sensing data. J. Geophys. Res. 2003. [Google Scholar] [CrossRef]
- Chédin, A.; Scott, N.A.; Wahiche, C.; Moulinier, P. The improved initialization inversion method: A high resolution physical method for temperature retrievals from satellites of the Tiros-N series. J. Appl. Meteorol. 1985, 24, 128–143. [Google Scholar] [CrossRef]
- Chevallier, F.; Cheruy, F.; Scott, N.A.; Chédin, A. A neural network approach for a fast and accurate computation of a longwave radiative budget. J. Appl. Meteorol. 1998, 37, 1385–1397. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Cristóbal, J.; Sobrino, J.A.; Sòria, G.; Ninyerola, M.; Pons, X. Revision of the single-channel algorithm for land surface temperature retrieval from Landsat thermal-infrared data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 339–349. [Google Scholar] [CrossRef]
- Li, Z.L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.; Tang, B.H.; Yan, G. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens. 2013, 34, 3084–3127. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N. Toward remote sensing methods for land cover dynamic monitoring: Application to Morocco. Int. J. Remote Sens. 2000, 21, 353–366. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Fujisada, H.; Kahle, A.B.; Tsu, H.; Kato, M.; Watanabe, H.; Kudoh, S.M. ASTER instrument performance, operation status, and application to Earth sciences. In Proceedings of IEEE International Geoscience and Remote Sensing Symposium, Sydney, NSW, Australia, 9–13 July 2001; pp. 1215–1216.
- ASTER Product Guide. Available online: http://gds.aster.ersdac.jspacesystems.or.jp/ (accessed on 19 April 2015).
- Wan, Z.; Li, Z.L. Radiance-based validation of the V5 MODIS land-surface temperature product. Int. J. Rem. Sens. 2008, 29, 5373–5395. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N.; Li, Z. A comparative study of land surface emissivity retrieval from NOAA data. Remote Sens. Environ. 2001, 75, 256–266. [Google Scholar] [CrossRef]
- Coll, C.; Wan, Z.; Galve, J.M. Temperature-based and radiance-based validation of the V5 MODIS land surface temperature product. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Ermida, S.L.; Trigo, I.F.; DaCamara, C.S.; Göttsche, F.M.; Olesen, F.S.; Hulley, G. Validation of remotely sensed surface temperature over an oak woodland landscape—The problem of viewing and illumination geometries. Remote Sens. Environ. 2014, 148, 16–27. [Google Scholar] [CrossRef]
- Todd, S.W.; Hoffer, R.M. Responses of spectral indices to variations in vegetation cover and soil background. Photogramm. Eng. Remote Sens. 1998, 64, 915–921. [Google Scholar]
- Timmermans, W.J.; Kustas, W.P.; Anderson, M.C.; French, A.N. An intercomparison of the Surface Energy Balance Algorithm for Land (SEBAL) and Two-Source Energy Balance (TSEB) modeling schemes. Remote Sens. Environ. 2007, 108, 369–384. [Google Scholar] [CrossRef]
- Zhou, J.; Hu, D.; Weng, Q. Analysis of surface radiation budget during the summer and winter in the metropolitan area of Beijing, China. J. Appl. Remote Sens. 2010. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, Y.; Zhang, X.; Zhan, W. Modelling the diurnal variations of urban heat islands with multi-source satellite data. Int. J. Remote Sens. 2013, 34, 7568–7588. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Li, M.; Liu, S.; Jia, Z.; Ma, Y. Validation and Performance Evaluations of Methods for Estimating Land Surface Temperatures from ASTER Data in the Middle Reach of the Heihe River Basin, Northwest China. Remote Sens. 2015, 7, 7126-7156. https://doi.org/10.3390/rs70607126
Zhou J, Li M, Liu S, Jia Z, Ma Y. Validation and Performance Evaluations of Methods for Estimating Land Surface Temperatures from ASTER Data in the Middle Reach of the Heihe River Basin, Northwest China. Remote Sensing. 2015; 7(6):7126-7156. https://doi.org/10.3390/rs70607126
Chicago/Turabian StyleZhou, Ji, Mingsong Li, Shaomin Liu, Zhenzhen Jia, and Yanfei Ma. 2015. "Validation and Performance Evaluations of Methods for Estimating Land Surface Temperatures from ASTER Data in the Middle Reach of the Heihe River Basin, Northwest China" Remote Sensing 7, no. 6: 7126-7156. https://doi.org/10.3390/rs70607126
APA StyleZhou, J., Li, M., Liu, S., Jia, Z., & Ma, Y. (2015). Validation and Performance Evaluations of Methods for Estimating Land Surface Temperatures from ASTER Data in the Middle Reach of the Heihe River Basin, Northwest China. Remote Sensing, 7(6), 7126-7156. https://doi.org/10.3390/rs70607126