1. Introduction
A lot of geomatic applications use DTMs as the basis to derive other products such as cartography, hydrological features, engineering solutions, urban planning, environmental studies, time series analyses, reports, statistics,
etc. The precision and accuracy of DTMs, required for deriving the above-mentioned products, however, may vary substantially. The data capture methodology is one key to explain the precision and accuracy of DTMs and how they influence the derived product. There is a need for reliable measures of accuracy allowing comparative evaluations of DTMs from different sources, e.g., LiDAR
versus photogrammetry. Most studies thus far focus on the height variable [
1,
2]. As the easiest variable to statistically compute and interpret, such studies focus on vertical accuracy. Some authors [
3,
4] studied the DEM accuracy as a function of some features (topographic index, hydrological objects). There are no reports to date of horizontal accuracy of DTMs or DEMs linked with the derived features, most likely because any such measure, if it exists, would hardly be applicable to other features [
5]. More recently, algorithms were defined to link the differences between horizontal accuracy and the derived parameters of features; such algorithms could be based on a triangulated irregular network (TIN) [
6,
7] or DEM grid models [
8]. The first approach generalizes the separation between homologous contours as the measure of horizontal discrepancy for the whole DEM, whereas the second compares several cells in two or more DEMs to estimate the horizontal discrepancy.
We can define the vertical accuracy for a DEM (grid structure composed of rows and columns) as the magnitude indicating how close the height of a point is, located by its horizontal position (row and column), on a DEM with respect its true value. If we have a reference DEM (RefDEM) as the ground truth we could estimate the vertical accuracy from any other DEM (CompDEM) just by computing the differences between the corresponding cell’s height from both DEMs. The vertical accuracy can be seen as the matrix: accMat = RefDEM − ComDEM. Horizontal accuracy is a little bit more complicated to understand because it may be difficult, given a point (RefP) on a RefDEM, to find its homologous point (HomP) on a CompDEM, except, for example, when RefP and HomP are a building corner, but that is not usually the case. We could understand the horizontal accuracy of a CompDEM with respect to its RefDEM; imagining the case where the CompDEM is identical to the RefDEM, then their contours would be the same. However, if we move the identical CompDEM horizontally, then the homologous contours from the CompDEM and RefDEM would not match and the discrepancy between the homologous contours indicates the horizontal discrepancy, which, consequently, is a measure of the horizontal accuracy. It is possible for each cell in the CompDEM to be horizontally displaced in any direction, so that homologous contours cross each other as shown in
Figure 1, where the area between homologous contours has been filled with gray color.
Figure 1.
Homologous contours (coming from homologous DEM: RefDEM and CompDEM) crossing each other and filling the area with gray color. The black color is a river piece.
Figure 1.
Homologous contours (coming from homologous DEM: RefDEM and CompDEM) crossing each other and filling the area with gray color. The black color is a river piece.
Both vertical and horizontal accuracy are important features to keep in every DEM because error in vertical and horizontal positioning could have bad consequences when, for example, computing flood risk areas. If we miscompute flood areas as a consequence of inaccurate DEMs, it would be possible to authorize, by error, the construction of some houses in flood risk areas. An illustration for both errors (vertical and horizontal inaccuracy) is shown in
Figure 2: on the left the real flood area has been computed, and the image on the upper right shows an error due to vertical inaccuracy (the CompDEM altitude is higher than the RefDEM altitude and an urban area is flooded); the image on the bottom right shows the error due to horizontal inaccuracy (the CompRef is moved to the left and up direction and an urban area is flooded). Another example of horizontal accuracy importance comes from the ability of LiDAR data to produce a highly detailed drainage network [
9] and it would be interesting to know the variation in the streams if computed with different DEM sources.
Landslide is another field where horizontal displacement has to be computed. There are several approaches to get such calculations, and one of them is based on series of images taken in different epochs, e.g., [
10,
11]. Those studies base their computation on minimizing a correlation function between a local window in the reference image and its homologous window in the compared image, according to the method explained by [
12].
In our present study we use an approach similar to that of [
8], but apply the particle image velocimetry (PIV) algorithm. PIV comes from a distant research field, more commonly used in studies involving aerodynamics [
13], transonic flows [
14], wind tunnels [
15], or aeroacoustic predictions [
16]. PIV can be used to determine the velocity field generated by a flow, tracking the particles inside that flow by repeated photography of the same area; an algorithm then computes the displacement of a particle (or a set of particles) from one photograph to the next. Dividing the particle displacement (number of pixels multiplied by the pixel size on the ground) by the time between photos gives us the velocity.
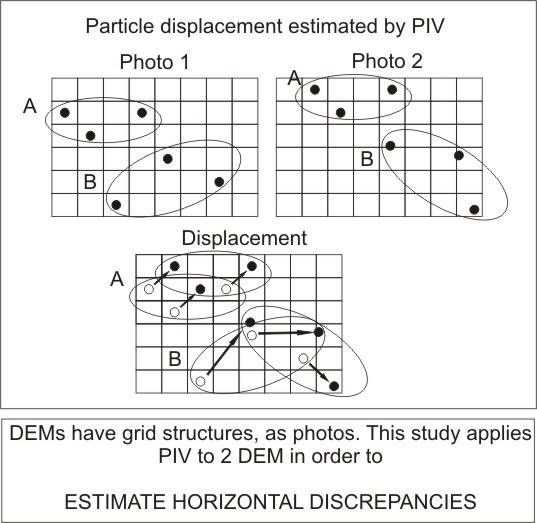
Figure 3 shows how two sets of particles are displaced from Photo 1 to Photo 2.
Figure 2.
Importance of vertical and horizontal accuracy.
Figure 2.
Importance of vertical and horizontal accuracy.
Figure 3.
Particle displacement derived from the position captured in two different photographs.
Figure 3.
Particle displacement derived from the position captured in two different photographs.
A DEM resembles a digital photograph in two ways:
- -
Both of them are made up of a regular grid of cells.
- -
Each cell is represented by a numerical value.
For these reasons, the PIV algorithm used on photos can almost directly be applied to DEMs. The only difference is that RGB (Red, Green, Blue) color photos must be transformed to a gray scale in the case of PIV, while DEM does not require transforming the cell values.
2. Materials and Methodology
In order to test the ability of PIV in estimating the horizontal displacement between two DEMs, we adopted the dataset used in [
8]. It consists of four samples (corresponding to four different places) pertaining to terrains with different slopes; they are labeled as upland, hill and mountain according to the classification from [
17]. Each sample is composed of two DEMs from two different sources: “Instituto Geográfico Nacional” (IGN) [
18] and “Instituto Cartográfico de Andalucía” (ICA) [
19], Spanish cartographic agencies at the national and regional level, respectively. The data captured correspond to the years 2005 (IGN) and 2004 (ICA). The cell size for the ICA DEMs is 10 m, and for the IGN ones it is 25 m. This means that the IGN DEMs must be resized in order to have the same dimensions in homologous DEMs (we will refer to homologous DEMs to the sample composed for the ICA and the IGN DEMs from the same place). Once we resize an IGN DEM, its cell size is the same as the ICA one, 10 m. There are several interpolating methods that could be used for resizing the IGN DEM, taking into account the cell neighborhood, e.g., the nearest, the bilinear or the bicubic. We decided to use the bicubic one, because the interpolating method influence on the estimated horizontal displacement is small, according to the study shown in
Section 3.1.
The names and the areas of each sample DEM are as follows: Seville (63.98 km
2), Huétor-Tájar (34.39 km
2), Colmenar (70.64 km
2) and Quéntar (51.85 km
2).
Table 1 shows the classification and the slope value for each place.
Table 1.
Slopes (%), heights (m) and category for each DEM from the dataset.
Table 1.
Slopes (%), heights (m) and category for each DEM from the dataset.
| Slope (%) | Terrain category | | Upland | Hill | Mountain |
| Places | | Seville | Huétor-Tájar | Colmenar | Quéntar |
| Cartographic Agencies | ICA (10 m cell size) | slope | 2.66 | 8.24 | 17.93 | 23.28 |
| Height | 50.29 | 566.4 | 367.30 | 1330.19 |
| IGN (25 m cell size) | slope | 2.53 | 8.4 | 17.41 | 22.11 |
| Height | 50.30 | 566.41 | 367.32 | 1330.25 |
To compare the PIV-estimated horizontal displacement (PIVEHD) with a reference displacement, we compute what we called the “real horizontal displacement” (RHD), which will be considered as the ground truth.
The RHD was computed by digitizing, as a polygonal shape (linear polyline), the same hydrological feature (creek or river) from the two DEM sources (ICA and IGN). Because both polygonals are in the same reference system (ETRS89 Datum) and they do not coincide exactly, the horizontal displacement can be computed as the area comprised between the two homologous polygonals and divided by their mean length. Each hydrological feature was digitized by four different people to enhance RHD accuracy. For the sake of redundancy we compute the RHD for four different hydrological features in each DEM (denoted as hydrological features 1, 2, 3 and 4 in
Table 2, distributed as shown in
Figure 4).
Table 2 shows the RHD between homologous hydrological features and their corresponding length; the last columns give the RHD mean value for each place, taking into account the four hydrological features.
Table 2.
Real displacement (RD) between homologous DEMs computed comparing linear hydrological features.
Table 2.
Real displacement (RD) between homologous DEMs computed comparing linear hydrological features.
| Hydrological Features | 1 | 2 | 3 | 4 | |
|---|
| Measures | RHD (m) | Length (m) | RHD (m) | Length (m) | RHD (m) | Length (m) | RHD (m) | Length (m) | (m) |
|---|
| Quéntar | 4.45 | 6416.92 | 4.75 | 7574.68 | 4.55 | 3530.28 | 4.01 | 2454.97 | 4.53 |
| Colmenar | 5.14 | 10,519.14 | 5.36 | 5180.19 | 4.99 | 3537.42 | 4.57 | 7054.26 | 5.01 |
| Huétor-Tájar | 5.03 | 3155.43 | 5.67 | 1356.23 | 5.18 | 2151.20 | 5.44 | 13,410.00 | 5.36 |
| Seville | 6.84 | 5279.10 | 6.55 | 3782.67 | 4.58 | 3527.30 | 5.01 | 14,224.70 | 5.53 |
Figure 4.
Sample DEMs (four different places) and distribution of the digitized linear hydrological features. Surrounding each hydrological feature is a buffer 600 m wide.
Figure 4.
Sample DEMs (four different places) and distribution of the digitized linear hydrological features. Surrounding each hydrological feature is a buffer 600 m wide.
It may be argued that applying the PIV to the whole DEM—comparing the PIVEHD of the entire DEM with the RHD from linear hydrological features—is an over-generalization. Hence, we computed the PIVEHD inside a buffer 600 m wide surrounding each hydrological feature. This was compared to the corresponding RHD. The size and shape of the buffers can be seen in
Figure 4.
Depending on the type of analysis needed, the PIV algorithm can be set with different parameters. A complete overview of PIV setting variability is found in [
20]. We opted to run the algorithm based on the cross-correlation function performed under Fast Fourier Transform (FFT), taking into account that displacement could entail translation (case A in
Figure 3) or a mixture of translation and rotation (case B in
Figure 3), as explained in [
20].
We used PIVlab software [
21] to arrive at parameters suitable for the above requirements.
The PIV method consists of defining an interrogation window in the first DEM (D) and displacing it over the second DEM (D′) around the original position of the window in D (
Figure 5).
Figure 5.
Interrogation window on the first DEM (D) and a displacement over the homologous DEM (D′).
Figure 5.
Interrogation window on the first DEM (D) and a displacement over the homologous DEM (D′).
The PIV algorithm attempts to find the best match between images (in our case DEMs D and D′) using the discrete cross-correlation function defined in Equation (1).
where H and H′ respectively represent the cell height in D and D′. For each displacement (x, y) selected, we obtain a
cross-correlation value. If we select a shift range
we obtain a correlation plane of size
. The cell value for the correlation plane is the sum of the products of all overlapping cells in D and D′. A graphic illustration is shown in
Figure 6. The best match would be the highest cell value in the correlation plane, and therefore the displacement is the corresponding (x, y) shifts that generated such a high cell value.
Figure 6.
Cross-correlation plane derived from the cross-correlation function using an interrogation window 4 × 4 in size.
Figure 6.
Cross-correlation plane derived from the cross-correlation function using an interrogation window 4 × 4 in size.
The cross-correlation function as expressed in Equation 1 has two weak points:
The solution to the first weak point is to compute the cross-correlation function as a complex conjugate multiplication of their Fourier transforms: , where and are the Fourier transforms from and .
The second weak point can be overcome using the cross-correlation coefficient, which normalizes the cross-correlation function and its definition as expressed by Equation (2):
where
The value is the average of the template and is computed only once while is the average of coincident with the template at position .
PIVlab [
21] software offers the option of applying a multiple pass interrogation window that improves the PIV results in the sense that more particle matching is achieved in the successive passes. Each pass decreases the interrogation window size. We tried three hierarchy passes, where in the next pass the interrogation window was one half of the previous one.
4. Conclusions
In our study we compute the horizontal displacement between two homologous DEMs coming from different sources. This is important because the horizontal discrepancy in both DEMs puts some derived features in non-corresponding places (e.g., hydrological linear features). Such discrepancies may be estimated by using the PIV algorithm as proposed in this paper. However, a larger number of cases must be computed in order to completely generalize our results. Our findings are a novelty in that an algorithm from the distant disciplines of aerodynamics or water flows is here applied to the DTM field.
The PIV algorithm underestimates the real horizontal displacement, but it does so in a scalar sense, which means that it as a scale factor can be used to arrive at a suitable estimation.
Using PIV and applying the scale factor, the error is around one-seventh of the cell size of the smaller DEMs (the ICA DEMs) and around one-nineteenth in the case of the larger cell size DEMs (the IGN DEMs). We consider these to be acceptable error values.
One remarkable finding is that the PIV approach provides reliable horizontal displacement values for nearly flat terrain types, which are the most difficult ones to compute due to their horizontal displacement.
The recommended interrogation windows are similar to those recommended in the original fields of PIV (aerodynamics, fluid mechanics...),
i.e., 32 × 32 [
20].
Future works along these lines will involve exploring PIV behavior in the horizontal displacement estimation between DEMs derived from LiDAR (very small cell sizes) and photogrammetry (cell sizes similar to the one used here). It would be interesting to determine whether the three interrogation window categories produce results that agree with the results presented here, or if new dimensions for the interrogation windows are necessary. In the case of LiDAR, because the cell size could be around a few centimeters, it would likely be better to use smaller features than hydrological ones, in order to compute the ground truth for the horizontal displacement, e.g., houses, buildings, fences, small dams, small pieces of roads. Another important point will be the computation time, because if we want to analyze a significant area, the file size will increase considerably, as will the PIV computation. Such a situation could need to parallelize some functions from the PIV software.