Pre-Launch Radiometric Characterization of JPSS-1 VIIRS Thermal Emissive Bands

Abstract

Pre-launch characterization and calibration of the thermal emissive spectral bands on the Joint Polar Satellite System (JPSS-1) Visible Infrared Imaging Radiometer Suite (VIIRS) is critical to ensure high quality data products for environmental and climate data records post-launch. A comprehensive test program was conducted at the Raytheon El Segundo facility in 2013–2014, including extensive environmental testing. This work is focused on the thermal band radiometric performance and stability, including evaluation of a number of sensor performance metrics and estimation of uncertainties. Analysis has shown that JPSS-1 VIIRS thermal bands perform very well in relation to their design specifications, and comparisons to the Suomi National Polar-orbiting Partnership (SNPP) VIIRS instrument have shown their performance to be comparable.

1. Introduction

The Visible Infrared Imaging Radiometer Suite (VIIRS) is a key sensor aboard the Joint Polar Satellite System (JPSS-1) mission, scheduled for launch in late 2016. JPSS-1 VIIRS is the second VIIRS instrument (the first currently flying on the SNPP (Suomi National Polar-orbiting Partnership) satellite [1,2]) and is the follow-on to heritage sensor MODIS [3]. VIIRS is a cross-track scanning radiometer capable of making continuous global observations twice daily. The sensor observes the Earth through 21 spectral bands and one pan-chromatic band covering a spectral range from 0.4 µm to 12.6 µm. These bands are used in support of a number of environmental data records covering land, ocean, and atmospheric science disciplines [4,5,6]. Seven of these spectral bands are considered thermal emissive (covering 3.7 µm to 12.6 µm) and are listed in Table 1 along with some of their characteristics. The performance and calibration of the VIIRS instrument thermal emissive bands pre-launch is critical to ensure high quality science data records are produced on-orbit, and that the calibration on-orbit is maintained. The pre-launch radiometric calibration and characterization of these thermal bands is the focus of this paper.

1.1. VIIRS Emissive Bands Overview

The VIIRS optical path from the entrance aperture, as viewed by the emissive bands, first passes though an afocal three mirror anastigmat and a fold mirror, known as the rotating telescope assembly (RTA) [1,7]. The RTA is a cross-track scanner that rotates once about every 1.78 s, viewing a ±56 degree swath through the Earth view (EV) port as well as three calibration views, each about 1 degree wide: a view of deep space (SV) used to determine the dark offset at about −66 degrees off nadir; a view of an on-board blackbody (referred to as the OBCBB) at about 100 degrees off nadir, used for on-orbit thermal band calibration; and a view of the solar diffuser at about 159 degrees off nadir, used for reflective band calibration on-orbit. The RTA directs the light onto a two-sided rotating fold mirror, known as the half angle mirror (HAM). The HAM, rotating at half the speed of the RTA, de-rotates the light beam and directs it into the fixed aft-optics. The light entering the aft-optics passes through a fold mirror, a four mirror anastigmat, and two dichroic beamsplitters. The first beamspitter reflects the visible and near-infrared light onto a focal plane assembly (FPA), while longer wavelengths pass through to the second dichroic beamsplitter. The second beamsplitter separates the short and mid-wave infrared (∼1–7 µm) from the long-wave infrared (∼7–16 µm), and directs the light onto two separate FPAs (via a steering mirror for the short and mid-wave infrared). Both of these FPAs will be cryogenically controlled at about 80.5 K on-orbit by means of a three-stage radiative cooler.

Table 1. VIIRS thermal bands with center wavelengths, bandwidths, gain mode, spatial resolution at nadir, upper and lower dynamic range limits, and typical scene temperature as defined by the sensor specification [8]. SG, HG, and LG refer to single gain, high gain, and low gain, respectively.

Band	Gain	Wavelength	Bandwidth	Resolution	$T_{\mathit{MIN}}$	$T_{\mathit{TYP}}$	$T_{\mathit{MAX}}$
	Mode	[nm]	[nm]	[m]	[K]	[K]	[K]
I4	SG	3740	380	375	210	270	353
I5	SG	11450	1900	375	190	210	340
M12	SG	3700	180	750	230	270	353
M13	HG	4050	155	750	230	300	343
M13	LG	4050	155	750	343	380	634
M14	SG	8550	300	750	190	270	336
M15	SG	10763	1000	750	190	300	340
M16	SG	12013	950	750	190	300	340

Table 1. VIIRS thermal bands with center wavelengths, bandwidths, gain mode, spatial resolution at nadir, upper and lower dynamic range limits, and typical scene temperature as defined by the sensor specification [8]. SG, HG, and LG refer to single gain, high gain, and low gain, respectively.

Band	Gain	Wavelength	Bandwidth	Resolution	$T_{\mathit{MIN}}$	$T_{\mathit{TYP}}$	$T_{\mathit{MAX}}$
	Mode	[nm]	[nm]	[m]	[K]	[K]	[K]
I4	SG	3740	380	375	210	270	353
I5	SG	11450	1900	375	190	210	340
M12	SG	3700	180	750	230	270	353
M13	HG	4050	155	750	230	300	343
M13	LG	4050	155	750	343	380	634
M14	SG	8550	300	750	190	270	336
M15	SG	10763	1000	750	190	300	340
M16	SG	12013	950	750	190	300	340

The emissive bands are located on the two temperature controlled FPAs: the mid-wave infrared (MWIR) bands I4, M12, and M13 are located on one FPA (along with five reflective bands covering ∼1.2 µm to 2.3 µm) and the long-wave infrared (LWIR) bands I5, M14, M15, and M16 are located on a dedicated FPA. All of the thermal bands use HgCdTe photo-voltaic detector arrays of 16 (or 32 for I4 and I5), staggered perpendicular to the direction of scan on the focal plane. A microlens focuses the light onto each detector after it passes through a spectral bandpass filter, defined by the center wavelength and bandpass listed in Table 1. Two bands, I4 and I5, are imaging bands with nadir resolutions of ∼375 m; the remaining thermal bands have resolutions of about 750 m at nadir. One band (M16) has two detector arrays (M16A and M16B) which are combined on-orbit through time-delayed integration. In addition, the 4.05 µm band M13 has two gain states (high and low); the M13 low gain stage is used to access very high temperature scenes (useful on-orbit for fire detection).

On-orbit, the calibration of the thermal bands is referenced to an internal blackbody, the OBCBB. The OBCBB is a V-groove blackbody with an emissivity above 99.6% in the spectral regions accessed by VIIRS thermal bands. The OBCBB is viewed once per scan and on-orbit will be controlled at a fixed temperature (∼292 K); it can also be cycled through a series of temperature levels between instrument ambient and 315 K. During pre-launch environmental testing, instrument ambient ranges from ∼253–276 K, while on-orbit instrument ambient is expected to be about 267 K (based on SNPP experience [1]).

1.2. Testing Overview

Before launch, a series of comprehensive performance tests were conducted for JPSS-1 VIIRS at the Raytheon El Segundo facility from 2012–2014 [9,10]. This work will focus on the radiometric portions of the test program performed under environmental conditions in the summer/fall of 2014. During the thermal vacuum test program, the bulk of testing was performed at three instrument temperature plateaus (referred to as cold, nominal, and hot) designed to cover the range of possible on-orbit conditions.

Four blackbodies were used as sources during radiometric testing. VIIRS thermal band calibration is referenced pre-launch to an external, NIST traceable blackbody (known as the BCS); the BCS is a cavity type blackbody with an emissivity greater than 99.96% and temperature levels ranging from 190 K to 345 K with a temperature uncertainty of less than 0.06 K (at 10 µm and 300 K). The BCS was located inside the thermal vacuum chamber at approximately 41 degrees scan angle. However, the BCS maximum temperature of 345 K was insufficient to characterize the M13 low gain state; as a result, an additional high temperature blackbody (referred to as the TMCBB), referenced to the BCS, was used for M13 low gain calibration. The TMCBB is an extended area, emissive source that was viewed through collimating optics located outside the thermal vacuum chamber and accessed temperatures ranging from laboratory ambient (about 294 K) up to 763 K. The TMCBB was viewed through a ZnSe window in the thermal vacuum chamber at about −1 degrees scan angle. In addition, an external cold target (known as the SVS) was used to simulate the deep space view. The SVS was located inside the thermal vacuum chamber, viewed at a scan angle of about −65.7 degrees, and controlled at approximately 90 K. The fourth and final blackbody was the OBCBB, which was described above.

The radiometric testing for the thermal bands can be divided into two sections: performance and stability (see Table 2). For the performance testing, the sources (either internal or external) were cycled through a series of discrete temperature levels; for stability testing, the source temperatures remained fixed while the instrument conditions were varied. The performance tests were used to determine the model coefficients relating the detector response to the radiance as well as assess a number of performance metrics, such as response non-linearity and detector-to-detector uniformity. The BCS and TMCBB were cycled through their respective temperature ranges as indicated in Table 2, while the OBCBB was fixed at 292 K. First the BCS was commanded through 12 discrete temperature settings from 190 K to 345 K; while this was happening, the TMCBB temperature also increased from laboratory ambient up to ∼375 K. The TMCBB temperature then continued to increase up to 763 K while the BCS temperature remained fixed at 345 K. Note that the TMCBB temperatures listed here refer to blackbody temperature and that the equivalent scene temperature at-aperture is lower. There were additional, special tests in which the BCS temperature was cycled at elevated focal plane temperatures (82 K and 83.5 K). In separate tests, the OBCBB was cycled from instrument ambient to 315 K in discrete temperature levels while the BCS and TMCBB temperatures were fixed (at about 300 K and laboratory ambient, respectively). After reaching 315 K, the OBCBB temperature control was turned off and the OBCBB was allowed to cool down to ∼292 K, during which data was also taken.

The stability tests were performed to check the instrument response to variations in operating conditions. For these tests, the BCS and OBCBB were commanded to fixed temperatures (300 K and 292 K, respectively). First, the instrument stability was tested versus time for about 3–8 h. The thermal band radiometric stability was also tested with respect to changes in the instrument temperatures while transitioning between plateaus. In particular, the stability was assessed with respect to the electronics temperature and instrument temperature. Stability was also investigated with respect to BUS voltage and FPA temperature changes.

Table 2. Radiometric testing performed for JPSS-1 VIIRS emissive bands during environmental testing [10]. C, N, and H refer to cold, nominal, and hot instrument plateaus; T refers to transitions between instrument plateaus. A and B denote the primary and redundant electronic hardware configuration settings.

Test	Instrument	Electronics	$T_{\mathit{BCS}}$	$T_{\mathit{TMCBB}}$	$T_{\mathit{OBCBB}}$	$T_{\mathit{FPA}}$	$V_{\mathit{BUS}}$
Type	Plateaus	Sides	[K]	[K]	[K]	[K]	[V]
Performance	C, N, H	A, B	190–345	294–375	292	80.5	28
Performance	N, H	A	190–345	294–375	292	82	28
Performance	N	A	190–345	294–375	292	83.5	28
Performance	C, N, H	A, B	345	388–763	292	80.5	28
Performance	C, N, H	A	300	294	Amb - 315	80.5	28
Stability	C, N, H	A, B	270	294	292	80.5	28
Stability	T	A	270	294	292	80.5	28
Stability	C, H	A, B	270	294	292	80.5	27–32
Stability	N	A	270	294	292	80.5–83.5	28

Table 2. Radiometric testing performed for JPSS-1 VIIRS emissive bands during environmental testing [10]. C, N, and H refer to cold, nominal, and hot instrument plateaus; T refers to transitions between instrument plateaus. A and B denote the primary and redundant electronic hardware configuration settings.

Test	Instrument	Electronics	$T_{\mathit{BCS}}$	$T_{\mathit{TMCBB}}$	$T_{\mathit{OBCBB}}$	$T_{\mathit{FPA}}$	$V_{\mathit{BUS}}$
Type	Plateaus	Sides	[K]	[K]	[K]	[K]	[V]
Performance	C, N, H	A, B	190–345	294–375	292	80.5	28
Performance	N, H	A	190–345	294–375	292	82	28
Performance	N	A	190–345	294–375	292	83.5	28
Performance	C, N, H	A, B	345	388–763	292	80.5	28
Performance	C, N, H	A	300	294	Amb - 315	80.5	28
Stability	C, N, H	A, B	270	294	292	80.5	28
Stability	T	A	270	294	292	80.5	28
Stability	C, H	A, B	270	294	292	80.5	27–32
Stability	N	A	270	294	292	80.5–83.5	28

2. Methodology

In this section, the methodology used to determine the radiometric model coefficients is reviewed, as well as the derivation of a number of performance and stability metrics. In addition, an uncertainty assessment is conducted on the radiance and brightness temperature products.

2.1. Radiometric Performance

The at-detector radiance when VIIRS views the BCS is the sum of the source radiance and the radiance from a number of emissive sources along the optical path (RTA, HAM, and aft optics) [7,11], or

$$\begin{array}{ccc}\hfill L_{BCS-path}& =& {\rho }_{RTA}·{\rho }_{HAM}·RV{S}_{BCS}·{\rho }_{aft}·{ϵ}_{BCS}·L_{BCS}\hfill \\ \hfill & & +\left(1-{\rho }_{RTA}\right){\rho }_{HAM}·RV{S}_{BCS}·{\rho }_{aft}·L_{RTA}\hfill \\ \hfill & & +\left(1-{\rho }_{HAM}·RV{S}_{BCS}\right){\rho }_{aft}·L_{HAM}+\left(1-{\rho }_{aft}\right)L_{aft}\hfill \end{array}$$

(1)

The reflectance factors (${\rho }_{RTA}$ and ${\rho }_{aft}$) represent the product of individual reflectances of the RTA and aft-optics surfaces respectively and ${ϵ}_{BCS}$ is the emissivity of the BCS. For VIIRS, the only optic that has a varying angle of incidence (AOI) is the HAM; here, the reflectance is represented by the product ${\rho }_{HAM}RVS$, where ${\rho }_{HAM}$ is the reflectance at the SV HAM AOI. $RVS$ is the AOI dependent, relative reflectance of the HAM [12]; in Equation (1), it is at the view angle of the BCS. The radiances of the sources (L) are determined via Planck’s law, convolved over the extended bandpass of the spectral transmittance of each band [13]. The temperature of each source is determined from one or more thermistors located on or near each component. Similarly, the at-detector radiance from the OBCBB and SV views are given by [7,11]

$$\begin{array}{ccc}\hfill L_{OBCBB-path}& =& {\rho }_{RTA}·{\rho }_{HAM}·RV{S}_{OBCBB}·{\rho }_{aft}·{ϵ}_{OBCBB}·L_{OBCBB}\hfill \\ \hfill & & +{\rho }_{RTA}·{\rho }_{HAM}·RV{S}_{OBCBB}·{\rho }_{aft}\left(1-{ϵ}_{OBCBB}\right)\hfill \\ \hfill & & \times \left(F_{RTA}·L_{RTA}+F_{SH}·L_{SH}+F_{CAV}·L_{CAV}\right)\hfill \\ \hfill & & +\left(1-{\rho }_{RTA}\right){\rho }_{HAM}·RV{S}_{OBCBB}·{\rho }_{aft}·L_{RTA}\hfill \\ \hfill & & +\left(1-{\rho }_{HAM}·RV{S}_{OBCBB}\right){\rho }_{aft}·L_{HAM}+\left(1-{\rho }_{aft}\right)L_{aft}\hfill \end{array}$$

(2)

and

$$\begin{array}{ccc}\hfill L_{SV-path}& =& \left(1-{\rho }_{RTA}\right){\rho }_{HAM}·RV{S}_{SV}·{\rho }_{aft}·L_{RTA}\hfill \\ \hfill & & +\left(1-{\rho }_{HAM}·RV{S}_{SV}\right){\rho }_{aft}·L_{HAM}+\left(1-{\rho }_{aft}\right)L_{aft}\hfill \end{array}$$

(3)

The cold reference target (SVS) was at a low enough temperature that the source radiance in the SV was negligible. The relative contributions of light reflected off the OBCBB into the path by the RTA, the blackbody shield (SH), and the scan cavity (CAV) are denoted by $F_{RTA}$, $F_{SH}$, and $F_{CAV}$, respectively. Here ${ϵ}_{OBCBB}$ is the emissivity of the OBCBB.

The path difference radiance between two sources (the latter of which is the SVS) is [7,11]

$$\begin{array}{ccc}\hfill \Delta L_{BCS}& =& \frac{L_{BCS-path}-L_{SV-path}}{{\rho }_{RTA}·{\rho }_{HAM}·{\rho }_{aft}}\hfill \\ \hfill & =& RV{S}_{BCS}·{ϵ}_{BCS}·L_{BCS}-\frac{\left(RV{S}_{BCS}-RV{S}_{SV}\right)}{{\rho }_{RTA}}\left[L_{HAM}-\left(1-{\rho }_{RTA}\right)L_{RTA}\right]\hfill \end{array}$$

(4)

and

$$\begin{array}{ccc}\hfill \Delta L_{OBCBB}& =& \frac{L_{OBCBB-path}-L_{SV-path}}{{\rho }_{RTA}·{\rho }_{HAM}·{\rho }_{aft}}\hfill \\ \hfill & =& RV{S}_{OBCBB}·{ϵ}_{OBCBB}·L_{OBCBB}\hfill \\ \hfill & & +RV{S}_{OBCBB}\left(1-{ϵ}_{OBCBB}\right)\left(F_{RTA}·L_{RTA}+F_{SH}·L_{SH}+F_{CAV}·L_{CAV}\right)\hfill \\ \hfill & & -\frac{\left(RV{S}_{OBCBB}-RV{S}_{SV}\right)}{{\rho }_{RTA}}\left[L_{HAM}-\left(1-{\rho }_{RTA}\right)L_{RTA}\right]\hfill \end{array}$$

(5)

Note that the aft optics radiance contribution canceled in the above equations as it is common to both paths and that the reflectance factors (RTA, HAM, and aft-optics) were absorbed into the left hand side of each equation.

The path difference radiance is modeled as a quadratic polynomial in the offset corrected digital response [7,11], or

$$\Delta L=c_0+c_1·dn+c_2·d{n}^2$$

(6)

Both the BCS and OBCBB were transitioned through a series of temperature levels; the data acquired was used to determine the coefficients by fitting the path difference radiance versus the detector response within the dynamic range (as discussed in Section 3.1). A check on the linearity of Equation (6) was performed by computing

$$NL=\frac{max\left({\Delta }_{fit}\right)}{L_{MAX}}$$

(7)

where the numerator is the maximum fitting residual for a linear fit and $L_{MAX}$ is the upper limit of the specified dynamic range.

The low gain state of band M13 cannot be calibrated using either the BCS or the OBCBB like the high gain state, so the high temperature external blackbody (TMCBB) was used. The TMCBB was tied to the BCS by cross calibration in the temperature range where both sources overlap (∼300–345 K), and then this calibration was extended to the high temperature region, using [7]

$$\begin{array}{ccc}\hfill \Delta L_{TMCBB}& =& RV{S}_{TMCBB}·{ϵ}_{TMCBB}·L_{TMCBB}+RV{S}_{TMCBB}\left(1-{\tau }_{TMC-op}\right)L_{TMC-op}\hfill \\ \hfill & & +RV{S}_{TMCBB}\left(1-{\rho }_{window}\right)L_{window}\hfill \\ \hfill & & -\frac{\left(RV{S}_{TMCBB}-RV{S}_{SV}\right)}{{\rho }_{RTA}}\left[L_{HAM}-\left(1-{\rho }_{RTA}\right)L_{RTA}\right]\hfill \end{array}$$

(8)

Additional source terms in the TMCBB path were included for the TMC optics ($L_{TMC-op}$) and the thermal vacuum chamber window ($L_{window}$), as the TMCBB was outside the thermal vacuum chamber. ${\rho }_{window}$ is the reflectance of the chamber window. The transmittance of the TMC optics (${\tau }_{TMC-op}$) was used to facilitate the calibration transfer from the BCS to the TMCBB. As with Equations (4) and (5), the reflectance factors (RTA, HAM, and aft-optics) were absorbed into the left hand side of the equation.

The radiometric sensitivity was determined by fitting the signal to noise ratio (SNR) to the path difference source radiance [7,11], or

$$SNR=\frac{\Delta L}{NEdL}=\frac{\Delta L}{\sqrt{k_0+k_1·\Delta L+k_2·\Delta L}}$$

(9)

As the BCS provided the more stable source, the SNR results derived from that source were closer to the true sensor SNR. The NEdT (the fluctuation in the scene temperature equivalent to the system noise) was computed by the equation

$$NEdT=\frac{\Delta L}{SNR·\frac{\partial L}{\partial T}}$$

(10)

The derivative is of Planck’s law with respect to the source temperature.

Inverting Equation (4) and substituting in Equation (6), the retrieved EV radiance is [7,11]

$$L_{EV-ret}=\frac{\left(c_0+c_1·dn+c_2·d{n}^2\right)}{RV{S}_{EV}}+\frac{\left(RV{S}_{EV}-RV{S}_{SV}\right)}{RV{S}_{EV}·{\rho }_{RTA}}\left[L_{HAM}-\left(1-{\rho }_{RTA}\right)L_{RTA}\right]$$

(11)

An additional factor,

$$\frac{\Delta L_{OBCBB}}{c_0+c_1·d{n}_{OBCBB}+c_2·d{n}_{OBCBB}^2}$$

(12)

is included on-orbit to adjust the calibration coefficients for scan-to-scan variations in the detector responsivity. For the purposes of this work, this factor will also be included when considering the uncertainty estimate in Section 2.3, so as to better estimate the expected on-orbit uncertainty. The detector-to-detector uniformity (or striping) is quantified by the following metric

$$RRU=\frac{\left|L_{EV-ret}-{〈L_{EV-ret}〉}_D\right|}{NEdL}$$

(13)

where the average EV retrieved radiance is over all detectors in a band and the NEdL was derived from Equation (9).

2.2. Radiometric Stability

Limited knowledge of how the instrument behaves with changing instrument conditions was obtained through performance testing. Stability tests were performed to more comprehensively investigate the impact of variations in instrument condition on the thermal band radiometry. The radiometric stability was assessed by trending the linear gain ($1/c_1$), derived from Equation (6) assuming $c_0$ and $c_2$ are negligible, or

$$\frac{1}{c_1}\cong \frac{dn}{\Delta L}$$

(14)

The linear gain was trended for all the stability cases listed in Table 2: with time, with changes in instrument temperature, with variation of the FPA temperature, and with changes in the BUS voltage. Assessments were made in terms of unit time, temperature, or voltage.

2.3. Uncertainty

The 1-sigma uncertainty of the retrieved EV radiance is estimated by propagating the uncertainty of the terms in Equation (11) following the methodology outlined in [14,15],

$$u^2\left(L_{EV-ret}\right)=\sum _{i=1}^N{\left(\frac{\partial L_{EV-ret}}{\partial x_i}\right)}^2{u}^2\left(x_i\right)+2\sum _{i=1}^{N-1}\sum _{j=i+1}^N\left(\frac{\partial L_{EV-ret}}{\partial x_i}\right)\left(\frac{\partial L_{EV-ret}}{\partial x_j}\right)u\left(x_i,x_j\right)$$

(15)

Here $u\left(x_i\right)$ is the uncertainty of the underlying variable $x_i$ that enters into the calculation of the radiance retrieval and $u(x_i,x_j)$ is the covariance between $x_i$ and $x_j$. The EV retrieved radiance was defined in Equation (11) and is a function of $c_0$, $c_1$, $c_2$, $L_{OBCBB}$, $L_{HAM}$, $L_{RTA}$, $L_{CAV}$, $L_{SH}$, $F_{SH}$, $F_{CAV}$, $F_{RTA}$, $RV{S}_{OBCBB}$, $RV{S}_{EV}$, $RV{S}_{SV}$, ${ϵ}_{OBCBB}$, ${\rho }_{RTA}$, $d{n}_{EV}$, and $d{n}_{OBCBB}$. Note that the total uncertainty here is for a single EV pixel; the effects of aggregation and scan angle were also investigated.

In general, the covariance terms were not directly calculated (the exception is the covariance terms between the radiometric coefficients $c_0$, $c_1$, and $c_2$); a direct calculation of these terms is beyond the scope of this work. However, an upper bound on the covariance terms is determined through use of the Schwarz inequality [14], or

$$\left|u\left(x_i,x_j\right)\right|\le u\left(x_i\right)u\left(x_i\right)$$

(16)

Results will be presented without covariance terms (excepting those terms between the radiometric coefficients) as a baseline and with covariance terms determined using the Schwarz inequality as a worst case estimate.

What follows is a brief description of the individual uncertainty contributors that enter into the full uncertainty analysis.

The radiance uncertainty for each of the radiances that factor into the present calculation ($L_{BCS}$, $L_{OBCBB}$, $L_{HAM}$, $L_{RTA}$, $L_{SH}$, and $L_{CAV}$) is the RSS of a number of uncertainty contributors. Each of these radiances was converted from a temperature provided by one or more thermistors once per scan (or for the external sources, temperature readings about every 10 s) using the Planck equation, integrated over the spectral response of each band [13]. The error is composed of four components: temperature, spectral, interpolation, and statistical uncertainties. The temperature uncertainties used in this analysis are 0.057 K, 0.03 K, 0.59 K, 9.0 K, 3.0 K, and 6.0 K, respectively [16]. The radiance uncertainty associated with each temperature error was determined by taking the absolute value of the difference between the Planck radiance with and without the temperature uncertainty, or

$$max\left|L\left(T,\lambda \right)-L\left(T\pm \Delta T,\lambda \right)\right|$$

(17)

The spectral errors used here are 1.2 nm for the MWIR bands and 4 nm for the LWIR bands [16]. The radiance uncertainties due to spectral errors were determined in the same manner as the temperature uncertainties,

$$max\left|L\left(T,\lambda \right)-L\left(T,\lambda \pm \Delta \lambda \right)\right|$$

(18)

On-orbit, the calibration relies on pre-calculated tables to convert source temperature to radiance with temperature intervals of 0.25 K. A linear interpolation is used to determine the radiance at the actual source temperature every scan. The interpolation uncertainty is determined by the following,

$$\frac{1}{2}\left(T-T_0\right)\left(T-T_1\right)f^{\left(2\right)}\left(T\right)$$

(19)

where $T_0$ and $T_1$ are the table values bracketing the measured T and the second derivative is of Planck’s radiation law with respect to the measured T. The statistical uncertainties were the standard deviation of the radiances determined within one data collection (or over 100 scans).

The RVS and its associated uncertainties were determined in earlier testing [12]. The derived RVS uncertainty was a combination of fitting error and measurement error; the band averaged values used in this work are 0.05%, 0.12%, 0.07%, 0.06%, 0.08%, 0.07%, 0.06% for bands I4–I5 and M12–M16. No uncertainty due to emission versus scan was included in the present work.

The uncertainties for the OBCBB reflectance shape factors are all taken to be 0.01 (the precision error of the calculation). The uncertainty for the reflectance of the RTA is 0.5% at 270 K [16]. This uncertainty was used for all source temperature levels. The OBCBB emissivity was measured at 3.39 µm; the error in the emissivity measurement was determined to be 0.04% for I4, M12, and M13, 0.05% for M14, and 0.06% for I5, M15, and M16 [16].

The uncertainty in the response was the RSS of the precision and accuracy errors for the background subtracted digital response. The precision error was the standard deviation over all analyzed samples and scans. The accuracy error was zero for the purposes of this work; any biases common to all sectors were removed in the background subtraction. The exception is a known bias between fixed and auto gain configurations for M13, which was not included in this work.

The vertical least-squares fitting algorithm used in this work determined the vertical deviations of the set of data points from the fit. The minimum of the vertical deviations was computed by setting the partial derivatives with respect to the coefficients equal to zero. This leads to the a matrix equation, the solution to which determined the radiometric coefficients in Equation (6). This algorithm also produced 1-sigma uncertainties and covariance terms. This approach assumes that the uncertainties in $\Delta L$ are roughly constant over the data points used (and uncertainties in $dn$ are negligible). However, this algorithm only included some effects from precision error (random statistical variations), but excluded any bias uncertainties (accuracy error). Furthermore, it should be noted that the uncertainties are valid only insomuch as the model itself is valid. An initial investigation into the quality of the model is discussed below. For the purposes of this work, the radiometric model is considered sufficiently valid to proceed with the uncertainty analysis.

The above procedure was followed at each instrument condition (temperature plateaus and electronics sides) as well as for both internal and external sources. In the present work, only the uncertainty derived using the BCS data is shown. On-orbit, the pre-launch radiometric coefficients will be used as a baseline, to which a scan-by-scan correction is applied (Equation (12)); the coefficients derived from the OBCBB during its warm-up/cool-down cycle will be used as a check on the calibration and replace the BCS coefficients only if a large change in behavior occurs.

2.4. Model Validity

As stated above, the radiometric fitting results are valid only insomuch as the model itself is valid. The functional form of the model was investigated by varying the order of the polynomial used in the fitting. Linear, quadratic, and cubic polynomials were employed. The full error analysis was conducted for each, and the results were compared to determine any relative improvement with increasing polynomial order. In addition, a parametric model was used to vary the source temperatures in the radiometric model in order to minimize the difference between the retrieved radiance and the source radiance determined from Planck’s radiation law. This would determine if there was any temperature bias between the BCS and OBCBB sources.

3. Results

3.1. Data Quality and Reduction

This section briefly describes the data selection and reduction performed to determine the radiometric fitting coefficients as well as the performance and stability metrics. The sensor specification defines the dynamic range over which VIIRS thermal bands must be calibrated [8]. However, valid science data may exist for some bands outside the specified range, and in some cases data inside the specified range is of low quality. In this work the fitted range was modified to include all available measured data not contaminated at high temperature by saturation and for which the SNR was greater than 5 at low temperature. The dynamic ranges are shown in Figure 1: the black lines represent the specified dynamic range; the red lines indicate the scene temperatures for which the SNR is equal to 5 (determined from Equation (9)) and the saturation temperatures; and the blue lines indicate the extent of the measurements used in the fitting. Note that the minimum and maximum BCS temperatures were 190 K and 345 K; these were in many cases limiting factors on modifying the fitting range. No band saturated below 345 K. However, the SNR fell below 5 inside the specified dynamic range for I4 (due to high noise, both 210 K and 230 K BCS levels were below the SNR threshold) and M14 (the large difference in RVS from SV to EV angle resulted in a negative offset corrected response at the lowest measured scene temperature). The lowest available measured levels that met the SNR threshold requirement for these two bands were 247 K (I4) and 210 K (M14). M13 low gain is not shown in Figure 1, but all available M13 low gain data was used in the fitting (TMCBB at-aperture scene temperatures from 355 K to 644 K). M13 low gain was not observed to saturate in thermal vacuum testing and the SNR was well above 5 at the lowest measured temperature.

Figure 1. Specified dynamic ranges shown for the VIIRS thermal bands (black lines). Maximum and minimum scene temperatures used in the fitting as shown with blue lines. Saturation and low temperature SNR threshold are also shown (red lines).

Figure 1. Specified dynamic ranges shown for the VIIRS thermal bands (black lines). Maximum and minimum scene temperatures used in the fitting as shown with blue lines. Saturation and low temperature SNR threshold are also shown (red lines).

Data collections were recorded at various source temperature levels, during each of which the source temperatures were stable (excepting when the OBCBB was cooling down). For each data collection, 100 scans were recorded (50 for each HAM side). For each scan and detector, 48 moderate resolution pixels were recorded for both the OBCBB view and SV (96 pixels for the imaging bands). The BCS and TMCBB views subtended a subset of the EV pixels. Each view was averaged over all valid pixels for a given scan. The SV was used as a dark reference which was subtracted from the signal in all other views to produce the $dn$. The $dn$ was then averaged over all valid scans in a given data collection. 1-sigma estimates were also determined for each $dn$, and the corresponding SNR was derived. Outlier rejection was performed at each stage of the calculation. The resulting $d{n}_{BCS}$, $d{n}_{OBCBB}$, and $d{n}_{TMCBB}$ were inserted into Equation (6).

VIIRS telemetry data was also extracted and averaged over all scans in each data collection. The telemetry data largely consisted of temperature readings, for both internal and external sources as well as instrument component temperatures. In some cases, more than one thermistor was used for a source in the thermal model; in those cases the average value was used. Data was supplied on the external sources (BCS, TMCBB, and SVS) about every 10 s, from which collection averaged temperature values were determined, and then radiances derived (a Planck function of the temperature reading convolved with the band averaged spectral response functions [13]) and inserted into the equations in Section 2. The telemetry of interest for the thermal model were the RTA, CAV, SH, and HAM temperatures as described in Section 2; these temperatures were also convolved with the band averaged spectral response functions and inserted into the equations in Section 2. Note that there was no direct temperature reading from the RTA, so that the CAV temperature was used with an instrument temperature dependent offset (∼4 K). Temperature data from the FPAs, electronics (ELEC), and instrument (OMM) was also collected, and used in the stability assessment.

Some of the input parameters, such as $RVS$ [12], ${ϵ}_{OBCBB}$, and ${\rho }_{RTA}$ [16], were measured in previous testing and their derivation will not be described in this work.

Once the component radiances were determined, the path difference radiances from Equations (4), (5), and (8) were computed. These path difference radiances and their corresponding $dn$ were then inserted into Equation (6), and fits of the radiometric calibration coefficients $c_i$ were performed over all valid data within the fitting range defined in Figure 1. These fit coefficients are next used to derive the retrieved radiance and performance metrics (non-linearity and uniformity). The SNR was also fit over the same range via Equation (9); this SNR fit was used to estimate the SNR and NEdT at $T_{TYP}$. Lastly, the uncertainty was propagated using Equation (15) and the various uncertainty contributors described in Section 2.3.

To determine the saturation and gain transition scene temperatures, partial views as VIIRS scanned across the BCS and TMCBB sources were used. Here the scan averaged dark offset was subtracted from each pixel of the scan across the sources profiles; the largest $dn$ was averaged over all scans in a data collection and then converted into a scene radiance using Equation (11), from which the scene temperature was determined via Planck’s law.

3.2. Radiometric Performance

The offset corrected detector response versus path difference radiance using BCS data for the MWIR bands, fit using a quadratic polynomial as described in Equation (6), are shown in Figure 2a for detector 9. The corresponding fitting residuals in % are shown in Figure 2b. For bands I4, M12, and M13 high gain, a significant portion of the 12 bit analog-to-digital converter (ADC) range was used. The radiance residuals for these bands increase at lower temperatures (worst case of up to ∼8% at 230 K for M12); the 230 K scene temperature translates to very low radiances in this spectral region, and this places a significant constraint on the fitting. M13 low gain (not shown) also exhibits this behavior at the low end of its measured range (near 355 K). Similarly, Figure 3a,b show the response versus radiance curves along with their corresponding radiance residuals in % for the LWIR bands using BCS data. For these bands, most of the 12 bit ADC range was used. The radiance residuals for these bands was generally small (less than 1% for all detectors, and much less when the lowest temperature level was excluded). The exception was detector 5 in M16B, which showed a higher residual than other detectors due to higher than average noise. All measured cases (instrument plateaus, electronics sides, HAM sides, and FPA temperatures as listed in Table 2) showed similar behavior in terms of fitting and residuals.

In general, the $c_0$ coefficient is on the order of ${10}^{-2}$ or less and is roughly consistent over plateaus and electronic sides. I5, M14, and M15 had the largest offsets with absolute values up to ∼0.03 [$W/m^2/sr/\mu m$]. The detector dependence is fairly stable versus instrument condition for the LWIR bands, while some variation with detector was observed for the MWIR bands. There is a good deal of detector variation in the $c_0$ trends versus instrument temperature. However, it should be noted that the variation of the offset with plateau is on the order of ${10}^{-2}$ or less. In the majority of cases, the 2-sigma error bars overlap for the different plateaus (electronics side dependent), indicating that $c_0$ is generally consistent over instrument temperature conditions. M14 is the exception, in that there appears to be some instrument temperature dependence. In addition, $c_0$ does not show any noticeable trend for the three FPA temperatures measured at nominal plateau, electronic side A (see Table 2). For M13 low gain, the derived $c_0$ was non-zero and positive (between 0 and 0.5 [$W/m^2/sr/\mu m$]).

Figure 2. The offset corrected detector response (a) and the radiance residual in % (b) shown versus path difference radiance. The symbols in (a) represent measured data and the lines indicate quadratic fits. The measured data was taken from nominal plateau, HAM side A, electronics side A, FPA temperature 80.5 K using detector 9 (BCS data).

Figure 2. The offset corrected detector response (a) and the radiance residual in % (b) shown versus path difference radiance. The symbols in (a) represent measured data and the lines indicate quadratic fits. The measured data was taken from nominal plateau, HAM side A, electronics side A, FPA temperature 80.5 K using detector 9 (BCS data).

The detector-to-detector patterns for the gains ($1/c_1$) are very consistent from instrument temperature plateau to plateau as well as across electronics side. In addition, there is a strong odd – even detector dependence observed in bands I5, M12, M13 (both high and low gain), and M15. The gains trend fairly linearly over instrument temperature plateau (see Table 3), with bands I4, M12, and M13 (both high and low gain) roughly consistent over plateaus and LWIR bands decreasing with instrument temperature. In general, the LWIR bands decrease by about 2% or less and the MWIR bands change by less than 1% over the ∼20 K measured instrument temperature range. Here the temperature variation is outside the 2-sigma error bars in most cases for the LWIR bands, but consistent for the MWIR bands. In addition, the electronics sides are not consistent for bands I5 and M14–M16. The gains determined at the three measured FPA temperatures for nominal plateau, electronics side A are consistent for bands I4, M12, and M13 high gain; however, for the LWIR bands, the gains decrease with increasing FPA temperature by between 3%–8% for every 1.5 K (see Table 3).

For the LWIR bands, the detector pattern of the nonlinear term ($c_2$) is roughly constant over plateau and electronics side; however, for the MWIR bands, the pattern is less well defined. In terms of magnitude, the nonlinear term is consistently on the order of ${10}^{-7}$ or less. For most bands and electronics sides, the nonlinear term exhibits a small, roughly linear increase with instrument temperature. There is some noticeable detector variation in the trending for the MWIR bands. In the majority of cases, the 2-sigma error bars overlap. The most glaring exception is M14. $c_2$ for the MWIR bands shows almost no change with FPA temperature, while $c_2$ increases with increasing FPA temperature for the LWIR bands.

Figure 3. The offset corrected detector response (a) and the radiance residual in % (b) shown versus path difference radiance. The symbols in (a) represent measured data and the lines indicate quadratic fits. The measured data was taken from nominal plateau, HAM side A, electronics side A, FPA temperature 80.5 K using detector 9 (BCS data).

Figure 3. The offset corrected detector response (a) and the radiance residual in % (b) shown versus path difference radiance. The symbols in (a) represent measured data and the lines indicate quadratic fits. The measured data was taken from nominal plateau, HAM side A, electronics side A, FPA temperature 80.5 K using detector 9 (BCS data).

The calibration coefficients derived using the OBCBB were compared to those computed from BCS data using a truncated fitting range that approximates the measured OBCBB range from instrument ambient to 315 K. For both cases, 2-sigma uncertainties were also determined for each coefficient. Comparing the two sets of calibration coefficients showed that for the majority of cases all three coefficients were within the 2-sigma uncertainties. Some detectors were exceptions in the following cases: the linear coefficient for M12 at cold and nominal instrument plateaus, the linear coefficient for M13 at hot instrument plateau, and the nonlinear coefficient for M14 at cold instrument plateau.

All of the thermal bands were shown to saturate above their design specifications [8] (see Table 4). All bands digitally saturate first, including both M13 gain stages; two bands (I4 and M12) exhibit analog saturation at some higher radiance within the measured range. For these two bands, the digital response decreases to zero at the highest measured radiance levels. On-orbit, this results in two possible values for a given digital response; fortunately, scenes with temperatures above saturation for these bands are usually fires, and can be correlated to M13 for quality control. The LWIR band saturation temperatures are generally consistent between different instrument plateaus to within ∼ 1 K and between electronics sides to within 2–3 K; for the MWIR bands, the separation between electronics sides is less clear, but all instrument conditions are consistent to within 2–3 K. The detector dependence is largely the reflection of the detector gain dependence. Bands I4, M12, and M14 saturate between 4 K and 10 K above the design specification; all other bands saturate more than 10 K above their design specifications.

Table 3. Averaged gains ($1/c_1$) over all detectors and HAM sides measured during radiometric performance testing for all instrument temperature plateaus, electronics sides (A or B), and focal plane temperatures using BCS data.

	Cold	Nominal	Nominal	Nominal	Hot	Hot	Cold	Nominal	Hot
Band	A	A	A	A	A	A	B	B	B
	80.5 K	80.5 K	82 K	83.5 K	80.5 K	82 K	80.5 K	80.5 K	80.5 K
I4	1134.6	1134.2	1133.8	1133.7	1134.3	1133.5	1134.0	1133.4	1134.3
I5	175.9	174.9	164.3	153.0	174.7	164.1	174.5	173.7	174.0
M12	1137.5	1137.1	1137.7	1138.4	1136.9	1137.5	1135.5	1135.6	1135.4
M13 HG	597.8	597.7	597.2	596.8	597.8	597.4	596.9	596.9	597.2
M13 LG	6.9	6.9	–	–	6.9	–	6.9	6.9	6.9
M14	175.1	174.2	162.5	149.0	173.4	161.6	172.3	171.4	170.5
M15	184.1	183.3	178.0	171.9	183.0	177.7	182.7	182.0	181.9
M16A	201.7	200.0	190.1	179.3	199.4	189.5	200.7	199.3	199.2
M16B	201.0	199.3	189.5	178.7	198.7	188.9	199.9	198.5	198.4

Table 3. Averaged gains ($1/c_1$) over all detectors and HAM sides measured during radiometric performance testing for all instrument temperature plateaus, electronics sides (A or B), and focal plane temperatures using BCS data.

	Cold	Nominal	Nominal	Nominal	Hot	Hot	Cold	Nominal	Hot
Band	A	A	A	A	A	A	B	B	B
	80.5 K	80.5 K	82 K	83.5 K	80.5 K	82 K	80.5 K	80.5 K	80.5 K
I4	1134.6	1134.2	1133.8	1133.7	1134.3	1133.5	1134.0	1133.4	1134.3
I5	175.9	174.9	164.3	153.0	174.7	164.1	174.5	173.7	174.0
M12	1137.5	1137.1	1137.7	1138.4	1136.9	1137.5	1135.5	1135.6	1135.4
M13 HG	597.8	597.7	597.2	596.8	597.8	597.4	596.9	596.9	597.2
M13 LG	6.9	6.9	–	–	6.9	–	6.9	6.9	6.9
M14	175.1	174.2	162.5	149.0	173.4	161.6	172.3	171.4	170.5
M15	184.1	183.3	178.0	171.9	183.0	177.7	182.7	182.0	181.9
M16A	201.7	200.0	190.1	179.3	199.4	189.5	200.7	199.3	199.2
M16B	201.0	199.3	189.5	178.7	198.7	188.9	199.9	198.5	198.4

Using Equation (9), the radiance at which the SNR was equal to 5 was calculated. The equivalent scene temperature was estimated, the band average of which is listed in Table 4 using nominal plateau data. For most bands this is below the design specifications [8]; the exceptions were I4 and M14. Estimates of the measured $T_{MIN}$ are consistent over instrument conditions. Note that there is some uncertainty in this estimate for bands I5, M13 low gain, M15, and M16 due to extrapolation well below the measured range.

The gain transition temperatures for M13 were measured to be between 343 and 349 K. There was about a 2 K spread in transition temperature with detector (largely due to detector-to-detector gain differences) and about a 3 K variation over instrument temperature (resulting from increasing background emission at higher instrument temperatures). This is slightly larger than the design specification [8], but has been deemed low risk to the science products.

The NEdT as a function of scene temperature is graphed in Figure 4 for all high gain bands (detector 9). The NEdT increases as the scene temperature decreases for all bands due to the influence of the derivative of the Planck function in Equation (10). For the LWIR bands, the NEdT is below ∼0.6 K, even at the lowest scene temperatures; for the MWIR bands, the NEdT increases to between 2.5–3.5 K for M12 and M13 at 210 K and roughly 3.5 K for I4 at 230 K. The NEdT is consistent across instrument conditions, except for the slight increase with instrument temperature due to increasing background emission. M13 low gain is not shown, but behaves similarly to the other bands; the NEdT is below ∼0.2 K for scene temperatures above about 400 K and increases to up to ∼0.5 K below 400 K. The elevated focal plane measurements had the effect of increasing the NEdT for the LWIR bands at all scene temperatures, with the greatest increases at low temperatures; in contrast, the MWIR bands showed very little difference in NEdT with increasing focal plane temperature.

The NEdT at $T_{TYP}$ for nominal plateau, electronic side A are listed in Table 4 (band maximum over detectors and HAM sides). The specified limit for NEdT at $T_{TYP}$ is also listed; all bands are well below the limit for all conditions. The only exception is detector 5 in band M16B, which is close to, but still below the specified limit. In addition, detector 4 in band M15 was consistently out-of-family. The NEdT at $T_{TYP}$ is very consistent over the range of instrument conditions tested, both in terms of magnitude and detector dependence. The NEdT generally increases with instrument temperature for all bands and both electronics sides (although there is a good deal of detector dependence). This is the result of the increasing background emission in the detectors which occurs at higher instrument temperatures. The NEdT at $T_{TYP}$ increases about 10% over the ∼20 K range of measured instrument temperatures (except for M12 which increases roughly 30%).

Figure 4. Plots show the measured NEdT as a function of scene temperature for the MWIR bands (a) and for the LWIR bands (b). Measured data was taken from nominal plateau, HAM side A, electronics side A, FPA temperature 80.5 K using detector 9.

Figure 4. Plots show the measured NEdT as a function of scene temperature for the MWIR bands (a) and for the LWIR bands (b). Measured data was taken from nominal plateau, HAM side A, electronics side A, FPA temperature 80.5 K using detector 9.

Table 4. Band maximum $NL$, NEdT at $T_{TYP}$, $T_{SAT}$, and $T_{MIN}$ measured during radiometric performance testing at the nominal instrument temperature plateau, electronics sides A, and 80.5 K focal plane temperature compared to their respective sensor specifications [8].

Band	$\mathit{NL}$ [%]		NEdT at $T_{\mathit{TYP}}$ [K]		$T_{\mathit{SAT}}$ [K]		$T_{\mathit{MIN}}$ [K]
	Meas	Spec	Meas	Spec	Meas	Spec	Meas	Spec
I4	0.1	1.0	0.428	2.500	357	353	231	210
I5	0.2	1.0	0.524	1.500	369	340	167	190
M12	0.2	1.0	0.131	0.396	359	353	216	230
M13 HG	0.2	1.0	0.046	0.107	363	343	213	230
M13 LG	0.1	1.0	0.231	0.423	644	634	276	343
M14	0.5	1.0	0.060	0.091	348	336	195	190
M15	0.2	1.0	0.035	0.070	357	340	173	190
M16A	0.2	1.0	0.045	0.072	366	340	154	190
M16B	0.5	1.0	0.072	0.072	367	340	156	190

Table 4. Band maximum $NL$, NEdT at $T_{TYP}$, $T_{SAT}$, and $T_{MIN}$ measured during radiometric performance testing at the nominal instrument temperature plateau, electronics sides A, and 80.5 K focal plane temperature compared to their respective sensor specifications [8].

Band	$\mathit{NL}$ [%]		NEdT at $T_{\mathit{TYP}}$ [K]		$T_{\mathit{SAT}}$ [K]		$T_{\mathit{MIN}}$ [K]
	Meas	Spec	Meas	Spec	Meas	Spec	Meas	Spec
I4	0.1	1.0	0.428	2.500	357	353	231	210
I5	0.2	1.0	0.524	1.500	369	340	167	190
M12	0.2	1.0	0.131	0.396	359	353	216	230
M13 HG	0.2	1.0	0.046	0.107	363	343	213	230
M13 LG	0.1	1.0	0.231	0.423	644	634	276	343
M14	0.5	1.0	0.060	0.091	348	336	195	190
M15	0.2	1.0	0.035	0.070	357	340	173	190
M16A	0.2	1.0	0.045	0.072	366	340	154	190
M16B	0.5	1.0	0.072	0.072	367	340	156	190

The non-linearity metric (NL) is generally consistent over instrument conditions and well below the specified limit (see Table 4). Detector 5 in M16B is again an outlier, but is still well below the 1.0% limit. M14 exhibits the largest average non-linearity at around 0.5%.

The potential for detector-to-detector striping was measured by the uniformity metric, graphed in Figure 5 for the worst case detector per band. A value greater then one indicates the potential for striping (dashed horizontal red line in the plots) [8]. The uniformity metric generally increases with increasing scene temperature, indicating increasing potential for striping as the temperatures rises. The potential for striping exists for many bands at the highest scene temperatures (in particular bands M13, M14, and M15). At higher temperatures, the deviation of the retrieved radiance from the band average increases, but the measured NEdL levels off (see Equation (13)); the result is a steadily increasing uniformity metric. On-orbit, the possibility of observing striping with M13 low gain is very limited, given the sparsity of measurements available.

Figure 5. Plots show the measured uniformity metric as a function of scene temperature for the MWIR bands (a) and for the LWIR bands (b). Measured data was taken from nominal plateau, HAM side A, electronics side A, FPA temperature 80.5 K using the worst case detector.

Figure 5. Plots show the measured uniformity metric as a function of scene temperature for the MWIR bands (a) and for the LWIR bands (b). Measured data was taken from nominal plateau, HAM side A, electronics side A, FPA temperature 80.5 K using the worst case detector.

3.3. Radiometric Stability

The radiometric stability of the JPSS-1 VIIRS instrument was tested for all the cases listed in Table 2. The first stability test listed in Table 2 assessed the instrument variation over time. In this case, the change in the linear gain is determined in the period between successive calibrations. On-orbit, successive calibrations of the linear gain occur every other scan for most thermal bands (M13 is calibrated every fourth scan) by observing the OBCBB. For all of the measured cases, the linear gain varied by under 0.0002% for all thermal bands (the total variation over the course of each test divided by the test time multiplied by the time it takes for two VIIRS scans).

For the stability tests that occurred over transitions between instrument temperature plateaus, the linear gain stability was assessed per degree K in terms of two different instrument temperatures (ELEC and OMM). There were three transition tests: the first from the lowest instrument temperature settings to the cold performance plateau (OMM temperatures ranging from 250–253 K and ELEC temperatures ranging from 262–268 K); the second from cold to nominal performance plateaus (OMM temperatures ranging from 253–262 K and ELEC temperatures ranging from 268–281 K); and the last from nominal to hot performance plateaus (OMM temperatures ranging from 263–273 K and ELEC temperatures ranging from 281–295 K). The linear gains varied by between 0.01%–0.04% (ELEC) and 0.04%–0.11% (OMM) per degree K. The transitions were performed such that the bulk of the ELEC temperture transition occured while the OMM temperature was roughly constant; similarly, most of the OMM temperature variation occured while the ELEC temperature change was small. This allowed the sensitivity to each temperature to be largely isolated and calculated separately. The sensitivity to each of these component temperatures will be included in the on-orbit calibration to remove any residual influences in the thermal model.

The third type of radiometric stability test performed varied the BUS voltage. In each case the BUS voltage was reduced from 32 to 27 Volts, with the sensor taking data at 1 Volt intervals. Results showed that the variation in linear gain was below 0.12% per Volt for all bands.

The last radiometric stability test listed in Table 2 corresponds to variations in the FPA temperatures. For this test, the FPA temperature was set to 83.5 K and then cooled down to 80.5 K (the expected on-orbit conditions). The linear gain for the MWIR bands showed very little change with FPA temperature (less than 0.16% per degree K). In contrast, the linear gain for the LWIR bands changed by between 2.4% (M15) to 6.4% (M14) per degree K. This is consistent with the radiometric performance results shown in Section 3.2.

3.4. Uncertainty

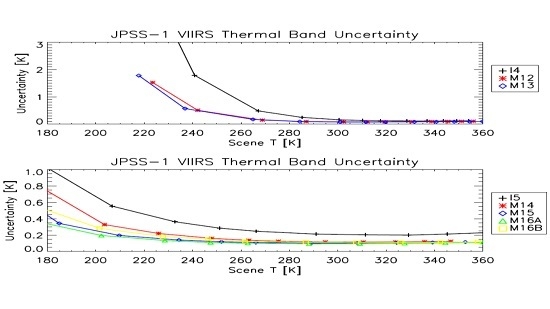
The total uncertainties for the EV retrieved radiance (for a single, un-aggregated pixel) are shown as a function of scene temperature in Figure 6 (worst case detector). For the MWIR bands, the results are between 0.1–0.2 K at high scene temperatures (above ∼290 K), but increase rapidly below scene temperatures of about 260–270 K (above about 1 K for I4 below 260 K and for M12 and M13 below 230 K). The LWIR bands uncertainty estimate is between 0.1–0.2 K above 250 K, below which the uncertainty rises slowly to between 0.3–0.5 K at 190 K. I5 shows a little higher uncertainty than the other LWIR bands, with 0.2–0.3 K above 250 K and slowly increasing up to about 0.8 K at 190 K. The calculated total uncertainties (in % radiance) are listed in Table 5 at the scene temperatures required by the design specifications; for most cases, the modeled uncertainty was below the design specifications [8]. The exceptions were bands M12 and M13 at both 230 and 270 K.

The uncertainties for the MWIR bands were dominated by contributions from two terms: $L_{OBCBB}$ and $d{n}_{EV}$. The $L_{OBCBB}$ uncertainty was roughly constant with scene temperature at about 0.3% and was dominant above ∼320 K for band I4 and about 290 K for the bands M12 and M13. The $d{n}_{EV}$ uncertainty increased rapidly as the scene temperature decreased and dominated the uncertainty at all other scene temperatures. As this estimate was for a single, un-aggregated pixel and this uncertainty contributor is largely a statistical error, this contribution will decrease when large data sets are used. In those cases, the uncertainties listed in Table 5 for M12 and M13 at both 230 and 270 K will fall below the design specifications. The $L_{OBCBB}$ uncertainty will then dominate above about 260 K for the bands I4, M12, and M13; at lower temperatures the largest contributor is the $c_0$ error, which increases rapidly as the scene temperature decreases. As a result, the reported uncertainties for these bands at low scene temperatures pose a low risk to the science products.

For most of the LWIR bands, there is no clearly dominant contributor at higher scene temperatures (above about 270 K). The exception is I5, where higher noise causes an increased contribution from the $d{n}_{EV}$ uncertainty at high scene temperatures. As with the MWIR bands, this contribution will decrease when large data sets are used. At lower scene temperatures, the main contributors are the $RVS$ and $d{n}_{EV}$ uncertainties, which all increase as the scene temperature decreases.

The impact of pixel aggregation and of scan angle was also investigated. For the bands in which the $d{n}_{EV}$ was the dominant contributor at some scene temperatures (I4, I5, M12, and M13 especially), pixel aggregation had the effect of reducing the uncertainty. In the bands for which the $RVS$ was a major contributor (bands M14 and M15), the uncertainty tended to be largest at the end of scan and lowest at the beginning of scan. Band M16 showed a mix of the two effects.

Figure 6. Plots show the modeled total temperature uncertainty as a function of scene temperature for the MWIR bands (a) and for the LWIR bands (b).

Figure 6. Plots show the modeled total temperature uncertainty as a function of scene temperature for the MWIR bands (a) and for the LWIR bands (b).

Table 5. Estimated uncertainty [% radiance] compared to the sensor specifications [8].

Band		190 K	230 K	267 K	270 K	310 K	340 K
I4	Spec	–	–	5.00	–	–	–
	Meas	–	–	2.64	–	–	–
I5	Spec	–	–	2.50	–	–	–
	Meas	–	–	0.48	–	–	–
M12	Spec	–	7.00	–	0.70	0.70	0.70
	Meas	–	9.14	–	0.78	0.35	0.33
M13	Spec	–	5.70	–	0.70	0.70	0.70
	Meas	–	7.81	–	0.78	0.29	0.27
M14	Spec	12.30	2.40	–	0.60	0.40	0.50
	Meas	2.86	0.73	–	0.30	0.20	0.18
M15	Spec	2.10	0.60	–	0.40	0.40	0.40
	Meas	1.35	0.41	–	0.20	0.15	0.13
M16A	Spec	1.60	0.60	–	0.40	0.40	0.40
	Meas	0.97	0.30	–	0.17	0.12	0.11
M16B	Spec	1.60	0.60	–	0.40	0.40	0.40
	Meas	1.46	0.41	–	0.20	0.14	0.12

Table 5. Estimated uncertainty [% radiance] compared to the sensor specifications [8].

Band		190 K	230 K	267 K	270 K	310 K	340 K
I4	Spec	–	–	5.00	–	–	–
	Meas	–	–	2.64	–	–	–
I5	Spec	–	–	2.50	–	–	–
	Meas	–	–	0.48	–	–	–
M12	Spec	–	7.00	–	0.70	0.70	0.70
	Meas	–	9.14	–	0.78	0.35	0.33
M13	Spec	–	5.70	–	0.70	0.70	0.70
	Meas	–	7.81	–	0.78	0.29	0.27
M14	Spec	12.30	2.40	–	0.60	0.40	0.50
	Meas	2.86	0.73	–	0.30	0.20	0.18
M15	Spec	2.10	0.60	–	0.40	0.40	0.40
	Meas	1.35	0.41	–	0.20	0.15	0.13
M16A	Spec	1.60	0.60	–	0.40	0.40	0.40
	Meas	0.97	0.30	–	0.17	0.12	0.11
M16B	Spec	1.60	0.60	–	0.40	0.40	0.40
	Meas	1.46	0.41	–	0.20	0.14	0.12

A covariance terms between the radiometric coefficients and the other contributors at the retrieved radiance level were estimated by using the Schwarz inequality as outlined in Equation (16). For all bands, the uncertainty only marginally increased at ∼292 K (where the calibration is tied to the OBCBB) and increased as the scene temperature increased or decreased. For the majority of modeled scene temperatures, the increase did not exceed 0.15%; the exceptions were the lowest scene temperatures for bands I4, M12, M13, and M14 as well as high temperature for band I4.

The impact of model validity was investigated by performing linear, quadratic, and cubic fits, and propagating the errors separately for each. In general, only marginal improvement in the uncertainty was derived by increasing the polynomial order from 2 to 3 (the biggest differences were at low temperature in the MWIR bands); in contrast, the quadratic model was a significant improvement over the linear (especially for M14). In addition, the differences between the EV retrieved radiance and BCS source radiance for all bands were minimized at 292 K by removing a bias of ∼27 mK from the OBCBB temperature.

3.5. Comparison to SNPP

In general, the performance of the thermal bands from SNPP VIIRS and JPSS-1 VIIRS are comparable. The radiometric fitting coefficients are very similar in magnitude for the thermal bands; there is greater dependence on detector for bands M15 and M16 in SNPP. M16B detector 5 is an outlier for JPSS-1, while M12 detector 1, M16A detector 9, and I5 detector 31 are outliers for SNPP. The band average saturation temperatures and the temperatures at which the SNR falls below 5 are fairly consistent between the two instruments (to within ∼5 K). The M13 gain transition temperatures exhibit a comparable spread with instrument conditions. The non-linearity of the radiometric fitting is consistent between the two sensors. Uniformity between detectors shows a similar pattern, with increasing potential for striping as the scene temperature increases. In addition, the uncertainties estimated for both sensors are in general agreement, with the uncertainty generally flat for the LWIR bands and the uncertainty for the MWIR increasing rapidly at low scene temperatures and relatively flat at high scene temperatures. Overall, the comparable pre-launch performance between the two sensors is likely to lead to JPSS-1 VIIRS thermal band science data products of as high a quality as is currently observed for SNPP VIIRS [7].

4. Conclusions

The JPSS-1 VIIRS instrument went through a comprehensive series of performance tests designed to characterize and calibrate the thermal emissive bands before launch at the Raytheon El Segundo facility. Accurate calibration of the VIIRS thermal emissive bands is necessary to ensure that the quality of the science and environmental data products is high. Assessment of the thermal band calibration has found that the instrument has met its design requirements for the majority of cases, and for those few cases where it does not, the risk to science data products is low. JPSS-1 VIIRS thermal band calibration pre-launch indicates that the products expected on-orbit will be comparable to the high quality science data that have been produced by the SNPP VIIRS thermal bands since it was launched in 2011.