Quantifying Multi-Decadal Change of Planted Forest Cover Using Airborne LiDAR and Landsat Imagery
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area

2.2. Data Collection and Preprocessing
2.2.1. Airborne LiDAR Data
2.2.2. Landsat TM and ETM+ Imagery
| Year | Julian Day | Day/Month | Year | Julian Day | Day/Month |
|---|---|---|---|---|---|
| 1986 | 159 | 9 June | 2003 | 190 | 10 July |
| 1987 | 258 | 16 September | 2004 | 241 | 29 August |
| 1989 | 199 | 19 July | 161 | 10 June | |
| 215 | 4 August | 2005 | 251 | 9 September | |
| 1990 | 138 | 19 May | 187 | 7 July | |
| 234 | 23 August | 2006 | 166 | 16 June | |
| 1993 | 258 | 16 September | 2007 | 153 | 3 June |
| 1994 | 181 | 1 July | 2008 | 244 | 1 September |
| 1995 | 264 | 22 September | 260 | 17 September | |
| 1998 | 181 | 1 July | 2009 | 190 | 10 July |
| 1999 | 267 | 25 September | 2010 | 193 | 13 July |
| 2000 | 206 | 25 July | 2011 | 228 | 17 August |
| 182 | 1 July | 2012 | 239 | 27 August | |
| 2001 | 152 | 2 June | 2013 | 177 | 27 June |
| 2002 | 235 | 24 August | 257 | 15 September |
2.2.3. Field Experiment Data
3. Method
3.1. Extracting Reference Forest Cover

3.2. Temporal Trajectory Construction
3.2.1. Spectral Indexes Extraction for the Time-Series Trajectory
3.2.2. Temporal Fitting of Spectral Indexes Trajectories
3.3. Forest Cover Modeling
3.4. Validation and Uncertainty Analysis
4. Results and Discussion
4.1. Performance of Forest Cover Regression Models in 2009

| Results with Ten-Fold Cross-Validation | ||||||
|---|---|---|---|---|---|---|
| R2 | RMSE | SD_R2 | SD_RMSE | ME | ||
| SLR | O | 0.50 | 9.29 | 0.034 | 0.34 | −0.006 |
| T | 0.59 | 8.48 | 0.027 | 0.17 | −0.002 | |
| QRNN | O | 0.54 | 8.75 | 0.033 | 0.29 | −0.021 |
| T | 0.65 | 7.84 | 0.022 | 0.29 | −0.042 | |
| SVM | O | 0.68 | 7.47 | 0.034 | 0.37 | −0.746 |
| T | 0.73 | 6.08 | 0.024 | 0.32 | −0.486 | |
| RF | O | 0.72 | 7.26 | 0.026 | 0.32 | 0.033 |
| T | 0.82 | 5.19 | 0.015 | 0.20 | −0.010 | |

4.2. Performance of Trajectory Landsat Imagery in Forest Cover Mapping

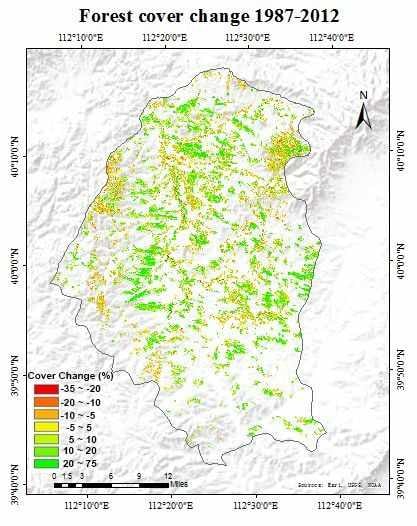
4.3. Forest Cover Change



4.4. Limitations
5. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.; Tyukavina, A.; Thau, D.; Stehman, S.; Goetz, S.; Loveland, T. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Gong, P.; Fu, R.; Zhang, M.; Chen, J.; Liang, S.; Xu, B.; Shi, J.; Dickinson, R. The role of satellite remote sensing in climate change studies. Nat. Clim. Chang. 2013, 3, 875–883. [Google Scholar] [CrossRef]
- Tokola, T.; Löfman, S.; Erkkilä, A. Relative calibration of multitemporal landsat data for forest cover change detection. Remote Sens. Environ. 1999, 68, 1–11. [Google Scholar] [CrossRef]
- Townshend, J.R.; Masek, J.G.; Huang, C.; Vermote, E.F.; Gao, F.; Channan, S.; Sexton, J.O.; Feng, M.; Narasimhan, R.; Kim, D. Global characterization and monitoring of forest cover using Landsat data: Opportunities and challenges. Int. J. Digit. Earth 2012, 5, 373–397. [Google Scholar] [CrossRef]
- Schroeder, T.A.; Cohen, W.B.; Yang, Z. Patterns of forest regrowth following clearcutting in western oregon as determined from a Landsat time-series. For. Ecol. Manag. 2007, 243, 259–273. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B.; Pfaff, E.; Braaten, J.; Nelson, P. Spatial and temporal patterns of forest disturbance and regrowth within the area of the northwest forest plan. Remote Sens. Environ. 2012, 122, 117–133. [Google Scholar] [CrossRef]
- Wang, X.; Huang, H.; Gong, P.; Liu, C.; Li, C.; Li, W. Forest canopy height extraction in rugged areas with ICESAT/GLAS data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4650–4657. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J.; Muller-Landau, H.C.; Vieilledent, G.; Vaudry, R.; Rasamoelina, M.; Hall, J.S.; van Breugel, M. A universal airborne Lidar approach for tropical forest carbon mapping. Oecologia 2012, 168, 1147–1160. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q. Retrieving vegetation height of forests and woodlands over mountainous areas in the pacific coast region using satellite laser altimetry. Remote Sens. Environ. 2010, 114, 1610–1627. [Google Scholar] [CrossRef]
- Huang, H.; Gong, P.; Cheng, X.; Clinton, N.; Li, Z. Improving measurement of forest structural parameters by co-registering of high resolution aerial imagery and low density Lidar data. Sensors 2009, 9, 1541–1558. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Huang, H.; Gong, P.; Wang, X.; Wang, J.; Li, W.; Li, C.; Li, Z. Joint use of ICESAT/GLAS and Landsat data in land cover classification: A case study in Henan province, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 511–522. [Google Scholar] [CrossRef]
- Huang, H.; Liu, C.; Wang, X.; Biging, G.S.; Yang, J.; Gong, P. Mapping vegetation heights in China with remotely sensed data. ISPRS J. Photogram. Remote Sens. 2016. Submitted. [Google Scholar]
- Chen, X.; Vierling, L.; Rowell, E.; DeFelice, T. Using Lidar and effective LAI data to evaluate Ikonos and Landsat 7 ETM+ vegetation cover estimates in a ponderosa pine forest. Remote Sens. Environ. 2004, 91, 14–26. [Google Scholar] [CrossRef]
- Ahmed, O.S.; Franklin, S.E.; Wulder, M.A. Integration of Lidar and Landsat data to estimate forest canopy cover in coastal British Columbia. Photogram. Eng. Remote Sens. 2014, 80, 953–961. [Google Scholar] [CrossRef]
- Sexton, J.O.; Song, X.-P.; Feng, M.; Noojipady, P.; Anand, A.; Huang, C.; Kim, D.-H.; Collins, K.M.; Channan, S.; DiMiceli, C. Global, 30-m resolution continuous fields of tree cover: Landsat-based rescaling of MODIS vegetation continuous fields with Lidar-based estimates of error. Int. J. Digit. Earth 2013, 6, 427–448. [Google Scholar] [CrossRef]
- Zhou, Q.; Robson, M.; Pilesjo, P. On the ground estimation of vegetation cover in australian rangelands. Int. J. Remote Sens. 1998, 19, 1815–1820. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L. Testing Lidar models of fractional cover across multiple forest ecozones. Remote Sens. Environ. 2009, 113, 275–288. [Google Scholar] [CrossRef]
- Koeln, G.T.; Jones, T.; Melican, J. Geocover Lc: Generating Global Land Cover from 7600 Frames of Landsat TM Data. In Proceedings of the ASPRS 2000 Annual Conference, Washington, DC, USA, 21–26 May 2000.
- Véga, C.; Durrieu, S. Multi-level filtering segmentation to measure individual tree parameters based on Lidar data: Application to a mountainous forest with heterogeneous stands. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 646–656. [Google Scholar] [CrossRef] [Green Version]
- FAO. Global Forest Resources Assessment 2000: Main Report; Food and Agriculture Organization of the United Nations: Rome, Italy, 2000. [Google Scholar]
- Smith, A.; Falkowski, M.J.; Hudak, A.T.; Evans, J.S.; Robinson, A.P.; Steele, C.M. A cross-comparison of field, spectral, and Lidar estimates of forest canopy cover. Can. J. Remote Sens. 2009, 35, 447–459. [Google Scholar] [CrossRef]
- Trost, J.E. Statistically nonrepresentative stratified sampling: A sampling technique for qualitative studies. Qual. Sociol. 1986, 9, 54–57. [Google Scholar] [CrossRef]
- Gao, B.-C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Jin, S.M.; Sader, S.A. Comparison of time series tasseled cap wetness and the normalized difference moisture index in detecting forest disturbances. Remote Sens. Environ. 2005, 94, 364–372. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Crist, E.P. A TM tasseled cap equivalent transformation for reflectance factor data. Remote Sens. Environ. 1985, 17, 301–306. [Google Scholar] [CrossRef]
- Powell, S.L.; Cohen, W.B.; Healey, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Ohmann, J.L. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modeling approaches. Remote Sens. Environ. 2010, 114, 1053–1068. [Google Scholar] [CrossRef]
- Liang, L.; Chen, Y.; Hawbaker, T.J.; Zhu, Z.; Gong, P. Mapping mountain pine beetle mortality through growth trend analysis of time-series Landsat data. Remote Sens. 2014, 6, 5696–5716. [Google Scholar] [CrossRef]
- Pflugmacher, D.; Cohen, W.B.; Kennedy, R.E.; Yang, Z. Using landsat-derived disturbance and recovery history and Lidar to map forest biomass dynamics. Remote Sens. Environ. 2014, 151, 124–137. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, S.; Sun, G. Forest biomass mapping of northeastern China using GLAS and MODIS data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 140–152. [Google Scholar] [CrossRef]
- Huang, C.; Peng, Y.; Lang, M.; Yeo, I.-Y.; McCarty, G. Wetland inundation mapping and change monitoring using Landsat and airborne Lidar data. Remote Sens. Environ. 2014, 141, 231–242. [Google Scholar] [CrossRef]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne Lidar. J. Geophys.Res. Biogeosci 2011, 116, G04021. [Google Scholar] [CrossRef]
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S.; et al. Finer resolution observation and monitoring of global land cover: First mapping results with landsat TM and ETM+ data. Int. J. Remote Sens. 2013, 34, 2607–2654. [Google Scholar] [CrossRef]
- Hao, P.; Zhan, Y.; Wang, L.; Niu, Z.; Shakir, M. Feature selection of time series MODIS data for early crop classification using random forest: A case study in Kansas, USA. Remote Sens. 2015, 7, 5347–5369. [Google Scholar] [CrossRef]
- Hao, P.; Wang, L.; Niu, Z. Potential of multitemporal Gaofen-1 panchromatic/multispectral images for crop classification: Case study in Xinjiang uygur autonomous region, China. J. Appl. Remote Sens. 2015, 9. [Google Scholar] [CrossRef]
- Fassnacht, F.; Hartig, F.; Latifi, H.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Fernández-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we need hundreds of classifiers to solve real world classification problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
- Ishwaran, H. Variable importance in binary regression trees and forests. Electron. J. Stat. 2007, 1, 519–537. [Google Scholar] [CrossRef]
- Breiman, L. Out-of-Bag Estimation; Technical Report; Citeseer: Berkeley, CA, USA, 1996. [Google Scholar]
- Díaz-Uriarte, R.; De Andres, S.A. Gene selection and classification of microarray data using random forest. BMC Bioinf. 2006, 7. [Google Scholar] [CrossRef]
- Sulla-Menashe, D.; Kennedy, R.E.; Yang, Z.; Braaten, J.; Krankina, O.N.; Friedl, M.A. Detecting forest disturbance in the Pacific northwest from MODIS time series using temporal segmentation. Remote Sens. Environ. 2014, 151, 114–123. [Google Scholar] [CrossRef]
- Alexander, C.; Bøcher, P.K.; Arge, L.; Svenning, J.-C. Regional-scale mapping of tree cover, height and main phenological tree types using airborne laser scanning data. Remote Sens. Environ. 2014, 147, 156–172. [Google Scholar] [CrossRef]
- Liu, S.; Gong, P. Change of surface cover greenness in China between 2000 and 2010. Chin. Sci. Bull. 2012, 57, 2835–2845. [Google Scholar] [CrossRef]
- Niinemets, Ü. Responses of forest trees to single and multiple environmental stresses from seedlings to mature plants: Past stress history, stress interactions, tolerance and acclimation. For. Ecol. Manag. 2010, 260, 1623–1639. [Google Scholar] [CrossRef]
- Dewar, R.C. Analytical model of carbon storage in the trees, soils, and wood products of managed forests. Tree Physiol. 1991, 8, 239–258. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Yuan, Y.; Liu, S.; Wang, Y.; Liu, L. Allocation of fine root biomass and its response to nitrogen deposition in poplar plantations with different stand ages. Chin. J. Ecol. 2007, 23, 185–189. [Google Scholar]
- Esseen, P.-A. Tree mortality patterns after experimental fragmentation of an old-growth conifer forest. Biol. Conserv. 1994, 68, 19–28. [Google Scholar] [CrossRef]
- Monserud, R.A.; Sterba, H. Modeling individual tree mortality for austrian forest species. For. Ecol. Manag. 1999, 113, 109–123. [Google Scholar] [CrossRef]
- Crowther, T.; Glick, H.; Covey, K.; Bettigole, C.; Maynard, D.; Thomas, S.; Smith, J.; Hintler, G.; Duguid, M.; Amatulli, G. Mapping tree density at a global scale. Nature 2015, 525, 201–205. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.-M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Huang, H.; Gong, P.; Biging, G.S.; Xin, Q.; Chen, Y.; Yang, J.; Liu, C. Quantifying Multi-Decadal Change of Planted Forest Cover Using Airborne LiDAR and Landsat Imagery. Remote Sens. 2016, 8, 62. https://doi.org/10.3390/rs8010062
Wang X, Huang H, Gong P, Biging GS, Xin Q, Chen Y, Yang J, Liu C. Quantifying Multi-Decadal Change of Planted Forest Cover Using Airborne LiDAR and Landsat Imagery. Remote Sensing. 2016; 8(1):62. https://doi.org/10.3390/rs8010062
Chicago/Turabian StyleWang, Xiaoyi, Huabing Huang, Peng Gong, Gregory S. Biging, Qinchuan Xin, Yanlei Chen, Jun Yang, and Caixia Liu. 2016. "Quantifying Multi-Decadal Change of Planted Forest Cover Using Airborne LiDAR and Landsat Imagery" Remote Sensing 8, no. 1: 62. https://doi.org/10.3390/rs8010062
APA StyleWang, X., Huang, H., Gong, P., Biging, G. S., Xin, Q., Chen, Y., Yang, J., & Liu, C. (2016). Quantifying Multi-Decadal Change of Planted Forest Cover Using Airborne LiDAR and Landsat Imagery. Remote Sensing, 8(1), 62. https://doi.org/10.3390/rs8010062