Global Gap-Free MERIS LAI Time Series (2002–2012)
Abstract
:1. Introduction
2. Input Data

3. Methods
3.1. LAI Retrieval and Aggregation
3.2. Harmonic Analysis
3.2.1. Single/Multi-Year Average

3.2.2. Outlier Detection
- The slope between data point i − 1 and i and the slope between data point i and i + 1 have opposite signs.
- One (or both) slope exceeds a value of ± , which has already been discussed as an unrealistic short time change in LAI [15].
3.2.3. Adjustment of the Time Series Length

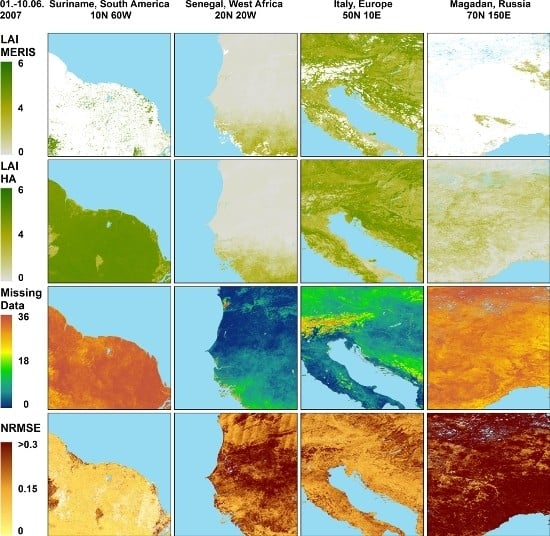
4. Exemplary Results

5. Results and Discussion
| Site | Country | Lat | Lon | LC | Date | |||
|---|---|---|---|---|---|---|---|---|
| Alpilles | France | 48.81 | 4.71 | Crops | 20 July 2002 | 1.7 | - | 1.3 |
| Barrax | Spain | 39.06 | −2.10 | Crops | 12 July 2003 | 1.0 | 2.1 | 0.8 |
| CHEQ | USA | 45.95 | −90.27 | EBF | 8 August 2002 | 3.0 | - | 3.8 |
| Chilbolton | GB | 51.10 | −1.26 | Crops | 10 June 2006 | 2.9 | 3.0 | 3.5 |
| Concepción | Chile | −37.28 | −73.28 | MF | 9 January 2003 | 3.2 | 3.1 | 4.4 |
| Counami | French Guiana | 5.34 | −53.24 | EBF | 13 October 2002 | 4.1 | - | 4.3 |
| Demmin | Germany | 53.89 | 13.21 | Crops | 23 July 2004 | 3.7 | - | 2.5 |
| Donga | Benin | 9.77 | 1.75 | Grass | 20 June 2005 | 1.8 | - | 1.6 |
| Fundulea | Romania | 44.41 | 26.59 | Crops | 24 May 2003 | 1.1 | 1.4 | 1.5 |
| Gnangara | Australia | −31.53 | 115.88 | EBF | 1 March 2004 | 1.0 | 0.6 | 1.1 |
| HARV | USA | 42.53 | −72.17 | MF | 24 August 2002 | 4.6 | - | 3.9 |
| Haouz | Morocco | 31.39 | −7.36 | Crops | 12 March 2003 | 1.3 | 0.1 | 1.2 |
| Hirsikangas | Finland | 62.38 | 27.00 | ENF | 14 August 2003 | 2.5 | - | 2.5 |
| 8 July 2004 | 1.5 | - | 2.6 | |||||
| 8 June 2005 | 1.4 | 3.2 | 2.5 | |||||
| Hyytiala | Finland | 61.51 | 24.18 | ENF | 6 July 2008 | 2.0 | 3.0 | 2.5 |
| Järvselja | Estonia | 58.30 | 27.26 | MF | 27 July 2003 | 4.2 | - | 3.6 |
| 29 June 2005 | 3.9 | 3.9 | 3.9 | |||||
| 22 March 2007 | 1.7 | - | 1.5 | |||||
| 18 August 2007 | 2.6 | - | 3.1 | |||||
| Laprida | Argentina | −36.59 | −60.33 | Grass | 19 October 2002 | 2.8 | - | 2.6 |
| Larose | Canada | 45.23 | −75.13 | MF | 7 August 2003 | 5.7 | - | 4.6 |
| NOBS | USA | 55.88 | −98.48 | EBF | 14 July 2002 | 3.3 | - | 3.6 |
| PlandeDieu | France | 44.20 | 4.95 | Crops | 7 July 2004 | 1.2 | 0.6 | 1.2 |
| Rovaniemi | Finland | 66.27 | 25.21 | ENF | 9 June 2004 | 1.2 | 1.5 | 2.1 |
| 15 June 2005 | 1.4 | 3.6 | 2.2 | |||||
| SEVI | USA | 34.35 | −106.70 | Grass | 26 July 2002 | 0.1 | - | 0.2 |
| 22 August 2002 | 0.3 | - | 0.3 | |||||
| 9 September 2002 | 0.4 | 0.0 | 0.2 | |||||
| 15 November 2002 | 0.3 | - | 0.2 | |||||
| 23 June 2003 | 0.1 | - | 0.1 | |||||
| 28 July 2003 | 0.1 | - | 0.1 | |||||
| 15 September 2003 | 0.1 | 0.2 | 0.1 | |||||
| 21 November 2003 | 0.1 | 0.0 | 0.1 | |||||
| Sonian | Belgium | 50.77 | 4.41 | MF | 26 June 2004 | 5.6 | 4.2 | 4.6 |
| TUND | USA | 71.28 | −156.61 | Tundra | 15 August 2002 | 1.1 | - | 1.3 |
| Turco | Bolivia | −18.24 | −68.19 | Grass | 15 March 2003 | 0.1 | - | 0.2 |
| Wankama | Niger | 13.65 | 2.64 | Grass | 23 June 2005 | 0.1 | 0.2 | 0.2 |




6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cayrol, P.; Kergoat, L.; Moulin, S.; Dedieu, G.; Chehbouni, A. Calibrating a coupled SVAT–vegetation growth model with remotely sensed reflectance and surface temperature—A case study for the HAPEX-sahel grassland sites. J. Appl. Meteorol. 2000, 39, 2452–2472. [Google Scholar] [CrossRef]
- Tucker, C.J.; Sellers, P.J. Satellite remote sensing of primary production. Int. J. Remote Sens. 1986, 7, 1395–1416. [Google Scholar] [CrossRef]
- Sellers, P.J.; Berry, J.A.; Collatz, G.J.; Field, C.B.; Hall, F.G. Canopy reflectance, photosynthesis, and transpiration. III. A reanalysis using improved leaf models and a new canopy integration scheme. Remote Sens. Environ. 1992, 42, 187–216. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hall, F.G.; Sellers, P.J.; Marshak, A.L. The interpretation of spectral vegetation indexes. IEEE Trans. Geosci. Remote Sens. 1995, 33, 481–486. [Google Scholar] [CrossRef]
- Sellers, P.J. Canopy reflectance, photosynthesis and transpiration. Int. J. Remote Sens. 1985, 6, 1335–1372. [Google Scholar] [CrossRef]
- Los, S.O.; Justice, C.O.; Tucker, C.J. A global 1° by 1° NDVI data set for climate studies derived from the GIMMS continental NDVI data. Int. J. Remote Sens. 1994, 15, 3493–3518. [Google Scholar] [CrossRef]
- Sellers, P.J.; Tucker, C.J.; Collatz, G.J.; Los, S.O.; Justice, C.O.; Dazlich, D.; Randall, D.A. A global 1° by 1° NDVI data set for climate studies. Part 2: The generation of global fields of terrestrial biophysical parameters from the NDVI. Int. J. Remote Sens. 2007, 15, 3519–3545. [Google Scholar] [CrossRef]
- Poulter, B.; Pederson, N.; Liu, H.; Zhu, Z.; D’Arrigo, R.; Ciais, P.; Davi, N.; Frank, D.; Leland, C.; Myneni, R.B.; et al. Recent trends in Inner Asian forest dynamics to temperature and precipitation indicate high sensitivity to climate change. Agric. For. Meteorol. 2013, 178–179, 31–45. [Google Scholar] [CrossRef]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.R.; Myneni, R.B. Global data sets of vegetation leaf area index (LAI)3g and fraction of photosynthetically active radiation (FPAR)3g derived from global inventory modeling and mapping studies (GIMMS) normalized difference vegetation index (NDVI3g) for the period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar]
- Fang, H.; Jiang, C.; Li, W.; Wei, S.; Baret, F.; Chen, J.M.; Garcia-Haro, J.; Liang, S.; Liu, R.; Myneni, R.B.; et al. Characterization and intercomparison of global moderate resolution leaf area index (LAI) products: Analysis of climatologies and theoretical uncertainties. J. Geophys. Res. Biogeosci. 2013, 118, 529–548. [Google Scholar] [CrossRef]
- Gao, F.; Morisette, J.T.; Wolfe, R.E.; Ederer, G.; Pedelty, J.; Masuoka, E.; Myneni, R.B.; Tan, B.; Nightingale, J. An algorithm to produce temporally and spatially continuous MODIS-LAI time series. IEEE Geosci. Remote Sens. Lett. 2008, 5, 60–64. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hoffman, S.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; Lotsch, A.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Baret, F.; Weiss, M.; Lacaze, R.; Camacho, F.; Makhmara, H.; Pacholcyzk, P.; Smets, B. GEOV1: LAI and FAPAR essential climate variables and FCOVER global time series capitalizing over existing products. Part1: Principles of development and production. Remote Sens. Environ. 2013, 137, 299–309. [Google Scholar] [CrossRef]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Niño, F.; Weiss, M.; Samain, O.; et al. LAI, fAPAR and fCover CYCLOPES global products derived from VEGETATION. Remote Sens. Environ. 2007, 110, 275–286. [Google Scholar] [CrossRef] [Green Version]
- Verger, A.; Baret, F.; Weiss, M. A multisensor fusion approach to improve LAI time series. Remote Sens. Environ. 2011, 115, 2460–2470. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of general regression neural networks for generating the GLASS leaf area index product from time-series MODIS surface reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, R.; Chen, J.M. Retrospective retrieval of long-term consistent global leaf area index (1981–2011) from combined AVHRR and MODIS data. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Pinty, B.; Andredakis, I.; Clerici, M.; Kaminski, T.; Taberner, M.; Verstraete, M.M.; Gobron, N.; Plummer, S.; Widlowski, J.-L. Exploiting the MODIS albedos with the two-stream inversion package (JRC-TIP): 1. Effective leaf area index, vegetation, and soil properties. J. Geophys. Res. 2011, 116, 1–20. [Google Scholar] [CrossRef]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Tesemma, Z.K.; Wei, Y.; Western, A.W.; Peel, M.C. Leaf area index variation for crop, pasture, and tree in response to climatic variation in the Goulburn–Broken catchment, Australia. J. Hydrometeor. 2014, 15, 1592–1606. [Google Scholar] [CrossRef]
- Turner, D.P.; Cohen, W.B.; Kennedy, R.E.; Fassnacht, K.S.; Briggs, J.M. Relationships between leaf area index and Landsat TM spectral vegetation indices across three temperate zone sites. Remote Sens. Environ. 1999, 70, 52–68. [Google Scholar] [CrossRef]
- Running, S.W.; Baldocchi, D.D.; Turner, D.P.; Gower, S.T.; Bakwin, P.S.; Hibbard, K.A. A global terrestrial monitoring network integrating tower fluxes, flask sampling, ecosystem modeling and EOS satellite data. Remote Sens. Environ. 1999, 70, 108–127. [Google Scholar] [CrossRef]
- Alton, P.B. From site-level to global simulation: Reconciling carbon, water and energy fluxes over different spatial scales using a process-based ecophysiological land-surface model. Agric. For. Meteorol. 2013, 176, 111–124. [Google Scholar] [CrossRef]
- Tum, M.; Günther, K.P.; McCallum, I.; Kindermann, G.; Schmid, E. Sustainable bioenergy potentials for Europe and the globe. Geoinf. Geo. Over. 2013, S1, 1–7. [Google Scholar]
- Dickinson, R.E. Land processes in climate models. Remote Sens. Environ. 1995, 51, 27–38. [Google Scholar] [CrossRef]
- Sellers, P.J.; Dickinson, R.E.; Randall, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A.; Sato, N.; et al. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Wang, D.; Wang, G.; Yang, W.; Liu, X. Regional differences in hydrological response to canopy interception schemes in a land surface model. Hydrol. Process. 2014, 28, 2499–2508. [Google Scholar] [CrossRef]
- Gobron, N.; Verstraete, M.M. Assessment of the Status of the Development of the Standards for the Terrestrial Essential Climate Variables: Leaf Area Index (LAI): Version 10; GTOS: Rome, Italy, 2009. [Google Scholar]
- Rüdiger, C.; Albergel, C.; Mahfouf, J.-F.; Calvet, J.-C.; Walker, J.P. Evaluation of the observation operator Jacobian for leaf area index data assimilation with an extended Kalman filter. J. Geophys. Res. 2010, 115, 1–10. [Google Scholar] [CrossRef]
- Barbu, A.L.; Calvet, J.-C.; Mahfouf, J.-F.; Albergel, C.; Lafont, S. Assimilation of Soil wetness index and leaf area index into the ISBA-A-gs land surface model: Grassland case study. Biogeosciences 2011, 8, 1971–1986. [Google Scholar] [CrossRef]
- Sabater, J.M.; Rüdiger, C.; Calvet, J.-C.; Fritz, N.; Jarlan, L.; Kerr, Y. Joint assimilation of surface soil moisture and LAI observations into a land surface model. Agric. For. Meteorol. 2008, 148, 1362–1373. [Google Scholar] [CrossRef] [Green Version]
- Jarlan, L.; Balsamo, G.; Lafont, S.; Beljaars, A.; Calvet, J.-C.; Mougin, E. Analysis of leaf area index in the ECMWF land surface model and impact on latent heat and carbon fluxes: Application to West Africa. J. Geophys. Res. 2008, 113, 1–22. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Garrigues, S.; Lacaze, R. LAI and fAPAR CYCLOPES global products derived from VEGETATION. Part 2: Validation and comparison with MODIS collection 4 products. Remote Sens. Environ. 2007, 110, 317–331. [Google Scholar] [CrossRef]
- Garrigues, S.; Lacaze, R.; Baret, F.; Morisette, J.T.; Weiss, M.; Nickeson, J.E.; Fernandes, R.A.; Plummer, S.E.; Myneni, R.B.; Yang, W. Validation and intercomparison of global Leaf Area Index products derived from remote sensing data. J. Geophys. Res. 2008, 113, 1–20. [Google Scholar] [CrossRef]
- Cohen, W.B.; Maiersperger, T.K.; Pflugmacher, D. BigFoot Leaf Area Index Surfaces for North and South American Sites, 2000–2003, Data Set; Oak Ridge National Laboratory Distributed Active Archive Center: Oak Ridge, TN, USA, 2006. Available online: http://www.daac.ornl.gov (accessed on 12 January 2016).
- VAlidation of Land European Remote Sensing Instruments (VALERI). Available online: http://w3.avignon.inra.fr/valeri/ (accessed on 8 January 2016).
- Fernandes, R.A.; Plummer, S.E.; Nightingale, J.; Baret, F.; Camacho, F.; Fang, H.; Garrigues, S.; Gobron, N.; Lang, M.; Lacaze, R.; et al. Global leaf area index product validation good practices. In Best Practice for Satellite-Derived Land Product Validation, Land Product Validation Subgroup (WGCV/CEOS), version 2.0.; Schaepman-Strub, G., Román, M.O., Nickeson, J.E., Eds.; CEOS: Zurich, Switzerland, 2014; pp. 1–78. [Google Scholar]
- Baret, F.; Morisette, J.T.; Fernandes, R.A.; Champeaux, J.L.; Myneni, R.B.; Chen, J.; Plummer, S.E.; Weiss, M.; Garrigues, S.; Nickeson, J.E. Evaluation of the representativeness of networks of sites for the global validation and intercomparison of land biophysical products: Proposition of the CEOS-BELMANIP. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1794–1803. [Google Scholar] [CrossRef]
- Roumenina, E.; Dimitrov, P.; Filchev, L.; Jelev, G. Validation of MERIS LAI and FAPAR products for winter wheat-sown test fields in North-East Bulgaria. Int. J. Remote Sens. 2014, 35, 3859–3874. [Google Scholar] [CrossRef]
- Dente, L.; Satalino, G.; Mattia, F.; Rinaldi, M. Assimilation of leaf area index derived from ASAR and MERIS data into CERES-Wheat model to map wheat yield. Remote Sens. Environ. 2008, 112, 1395–1407. [Google Scholar] [CrossRef]
- Bacour, C.; Baret, F.; Béal, D.; Weiss, M.; Pavageau, K. Neural network estimation of LAI, fAPAR, fCover and LAI×Cab, from top of canopy MERIS reflectance data: Principles and validation. Remote Sens. Environ. 2006, 105, 313–325. [Google Scholar] [CrossRef]
- Canisius, F.; Fernandes, R.A.; Chen, J. Comparison and evaluation of Medium Resolution Imaging Spectrometer leaf area index products across a range of land use. Remote Sens. Environ. 2010, 114, 950–960. [Google Scholar] [CrossRef]
- Dilmaghani, S.; Henry, I.C.; Soonthornnonda, P.; Christensen, E.R.; Henry, R.C. Harmonic analysis of environmental time series with missing data or irregular sample spacing. Environ. Sci. Technol. 2007, 41, 7030–7038. [Google Scholar] [CrossRef] [PubMed]
- Scargle, J.D. Studies in astronomical time series analysis. I—Modeling random processes in the time domain. Astrophys. J. Suppl. Ser. 1981, 45, 1–71. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-squares frequency analysis of unequally spaced data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- Yuan, H.; Dai, Y.; Xiao, Z.; Ji, D.; Wei, S.G. Reprocessing the MODIS Leaf Area Index products for land surface and climate modelling. Remote Sens. Environ. 2011, 115, 1171–1187. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Kandasamy, S.; Baret, F.; Verger, A.; Neveux, P.; Weiss, M. A comparison of methods for smoothing and gap filling time series of remote sensing observations—Application to MODIS LAI products. Biogeosciences 2013, 10, 4055–4071. [Google Scholar] [CrossRef]
- Roerink, G.J.; Menenti, M.; Verhoef, W. Reconstructing cloudfree NDVI composites using Fourier analysis of time series. Int. J. Remote Sens. 2000, 21, 1911–1917. [Google Scholar] [CrossRef]
- Colditz, R.R.; Conrad, C.; Wehrmann, T.; Schmidt, M.; Dech, S.W. TiSeG: A flexible software tool for time-series generation of MODIS data utilizing the quality assessment science data set. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3296–3308. [Google Scholar] [CrossRef]
- Moffat, A.M.; Papale, D.; Reichstein, M.; Hollinger, D.Y.; Richardson, A.D.; Barr, A.G.; Beckstein, C.; Braswell, B.H.; Churkina, G.; Desai, A.R.; et al. Comprehensive comparison of gap-filling techniques for eddy covariance net carbon fluxes. Agric. For. Meteorol. 2007, 147, 209–232. [Google Scholar] [CrossRef]
- Hird, J.N.; McDermid, G.J. Noise reduction of NDVI time series: An empirical comparison of selected techniques. Remote Sens. Environ. 2009, 113, 248–258. [Google Scholar] [CrossRef]
- Musial, J.P.; Verstraete, M.M.; Gobron, N. Technical note: Comparing the effectiveness of recent algorithms to fill and smooth incomplete and noisy time series. Atmos. Chem. Phys. 2011, 11, 7905–7923. [Google Scholar] [CrossRef] [Green Version]
- Fang, H.; Liang, S.; Townshend, J.R.G.; Dickinson, R.E. Spatially and temporally continuous LAI data sets based on an integrated filtering method: Examples from North America. Remote Sens. Environ. 2008, 112, 75–93. [Google Scholar] [CrossRef]
- Bittner, M.; Offermann, D.; Bugaeva, I.V.; Kokin, G.A.; Koshelkov, J.P.; Krivolutsky, A.; Tarasenko, D.A.; Gil-Ojeda, M.; Hauchecorne, A.; Lübken, F.-J.; et al. Long period/large scale oscillations of temperature during the DYANA campaign. J. Atmos. Terr. Phys. 1994, 56, 1675–1700. [Google Scholar] [CrossRef]
- Meisner, R.E.; Bittner, M.; Dech, S.W. Computer animation of remote sensing-based time series data sets. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1100–1106. [Google Scholar] [CrossRef]
- Erbertseder, T.; Eyring, V.; Bittner, M.; Dameris, M.; Grewe, V. Hemispheric ozone variability indices derived from satellite observations and comparison to a coupled chemistry-climate model. Atmos. Chem. Phys. 2006, 6, 5105–5120. [Google Scholar] [CrossRef]
- European Space Agency (ESA). Envisat MERIS FRS Density Maps. 2014. Available online: https://earth.esa.int/web/guest/-/envisat-meris-frs-density-maps (accessed on 7 January 2016).
- ACRI-ST. AMORGOS (Accurate MERIS Ortho-Rectified Geo-Location Operational Software) Versions 3.0 and 4.0. 2012. Available online: https://earth.esa.int/web/guest/-/amorgos-40p1–4410 (accessed on 7 January 2016).
- Muller, J.-P.; López, G.; Potts, D.; Shane, N.; Kharbouche, S.; Fisher, D.; Lewis, P.; Brockmann, C.; Danne, O.; Krüger, O.; et al. GlobAlbedo: Theoretical Basis Document V4_12; London’s Global University: London, UK, 2013. [Google Scholar]
- Baret, F.; Pavageau, K.; Béal, D.; Weiss, M.; Berthelot, B.; Regener, P. Algorithm Theoretical Basis Document for MERIS Top of Atmosphere Land Products; INRA-CSE: Avignon, France, 2006. [Google Scholar]
- Pinty, B.; Gobron, N.; Mélin, F.; Vestraete, M.M. A Time Composite Algorithm for FAPAR Products: Theoretical Basis Document; Institute for Environment and Sustainability, Joint Research Centre: Ispra, Italy, 2002. [Google Scholar]
- Fomferra, N. The BEAM Graph Processing Framework. 2013. Available online: http://www.brockmann-consult.de/beam/doc/help-4.11/ (accessed on 9 October 2014).
- Dean, J.; Ghemawat, S. MapReduce: Simplified data processing on large clusters. In Proceeding of the 6th Symposium on Operating Systems Design and Implementation, San Francisco, CA, USA, 6–8 December 2004; pp. 137–149.
- Böttcher, M.; Fomferra, N.; Zühlke, M.; Brockmann, C. Fast processing and exploitation of full mission datasets for ESA-CCI. In Proceeding of the 3rd MERIS/(A)ATSR & OCLI-SLSTR Preparatory Workshop, Frascati, Italy, 15–19 October 2012.
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Golub, G.H.; van Loan, C.F. Matrix Computations (3rd Ed.); Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Arino, O.; Ramos, J.; Kalogirou, V.; Defourny, P.; Achard, F. GlobCover 2009. In Proceeding of the ESA Living Planet Symposium, Bergen, Norway, 27 June–2 July 2009.
- Schneider, K. Die Aufbereitung Von Digitalen Fernerkundungsdaten Zur Quantitativen Bestimmung des Chlorophyll- und Schwebstoffgehalts in Einem Kleinen Süßwassersee. Diploma Thesis, University of Freiburg im Breisgau, Freiburg, Germany, 1987. [Google Scholar]
- Tetzlaff, G.; Peters, M. The atmospheric transport potential for water vapour and dust in the Sahel region. GeoJournal 1986, 12, 387–398. [Google Scholar] [CrossRef]
- Kandji, S.T.; Verchot, L.V.; Mackensen, J. Climate Change and Variability in the Sahel Region: Impacts and Adaptation Strategies in the Agricultural Sector; UNEP & ICRAF: Nairobi, Kenya, 2006. [Google Scholar]
- Morisette, J.T.; Baret, F.; Privette, J.L.; Myneni, R.B.; Nickeson, J.E.; Garrigues, S.; Weiss, M.; Fernandes, R.A.; Leblanc, S.G.; Kalacska, M.; et al. Validation of global moderate-resolution LAI products: A framework proposed within the CEOS land product validation subgroup. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1804–1817. [Google Scholar] [CrossRef]
- Garrigues, S.; Shabanov, N.V.; Swanson, K.; Morisette, J.T.; Baret, F.; Myneni, R.B. Intercomparison and sensitivity analysis of Leaf Area Index retrievals from LAI-2000, AccuPAR, and digital hemispherical photography over croplands. Agric. For. Meteorol. 2008, 148, 1193–1209. [Google Scholar] [CrossRef]
- Wißkirchen, K.; Tum, M.; Günther, K.P.; Niklaus, M.; Eisfelder, C.; Knorr, W. Quantifying the carbon uptake by vegetation for Europe on a 1 km2 resolution using a remote sensing driven vegetation model. Geosci. Model Dev. 2013, 6, 1623–1640. [Google Scholar] [CrossRef]
- Tum, M.; Günther, K.P.; Böttcher, M.; Baret, F.; Bittner, M.; Brockmann, C.; Weiss, M. MERIS—Gap free leaf area index (LAI). Available online: http://dx.doi.org/10.15489/ak90g1wty909 (accessed on 8 January 2016).
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tum, M.; Günther, K.P.; Böttcher, M.; Baret, F.; Bittner, M.; Brockmann, C.; Weiss, M. Global Gap-Free MERIS LAI Time Series (2002–2012). Remote Sens. 2016, 8, 69. https://doi.org/10.3390/rs8010069
Tum M, Günther KP, Böttcher M, Baret F, Bittner M, Brockmann C, Weiss M. Global Gap-Free MERIS LAI Time Series (2002–2012). Remote Sensing. 2016; 8(1):69. https://doi.org/10.3390/rs8010069
Chicago/Turabian StyleTum, Markus, Kurt P. Günther, Martin Böttcher, Frédéric Baret, Michael Bittner, Carsten Brockmann, and Marie Weiss. 2016. "Global Gap-Free MERIS LAI Time Series (2002–2012)" Remote Sensing 8, no. 1: 69. https://doi.org/10.3390/rs8010069
APA StyleTum, M., Günther, K. P., Böttcher, M., Baret, F., Bittner, M., Brockmann, C., & Weiss, M. (2016). Global Gap-Free MERIS LAI Time Series (2002–2012). Remote Sensing, 8(1), 69. https://doi.org/10.3390/rs8010069