1. Introduction
Forests take carbon dioxide from the atmosphere and help reduce greenhouse effects and control global climate change [
1,
2]. Thus, there is a strong need to estimate forest carbon density (stock per area unit). Moreover, as carbon marketing develops at global, regional and local scales, generating the spatial distributions or maps of forest carbon density and assessing their accuracy have to be conducted at multiple spatial resolutions [
1,
2,
3]. This requires field observations of forest carbon density to be collected at the corresponding spatial resolutions to match the map units, which is very time-consuming and costly. Instead, field observations are often obtained from sample plots that have a fixed size. This will lead to inconsistency of spatial resolutions between sample plots and map units, making it challenging for the multi-resolution mapping and accuracy assessment of forest carbon density.
Substantial research has been conducted and various methods have been developed to estimate forest carbon density at different spatial and temporal scales [
1,
3,
4,
5,
6,
7,
8,
9]. The widely used methods include: (1) traditional forest carbon estimations based on field measurements from sample plots, leading to population estimates [
10]; (2) eddy correlation and covariance based methods, measuring carbon flux [
9,
11]; and (3) process model-based methods, simulating sequestration of carbon and accumulation of biomass [
12,
13]. All of these methods lack the ability to produce the spatial distributions of forest carbon density without combination of remotely sensed images. Thus, combining sample plot and image data shows greater potential to map forest carbon density because it can produce an estimate of each location over large areas [
9,
14,
15,
16]. Regression is a most commonly used method that combines plot data and images to map forest carbon density [
9,
17,
18,
19], but this method often leads to illogical negative and extremely large estimates [
19]. Wang et al. [
20] proposed an image-based co-simulation algorithm to map forest carbon density by combining sample plot and image data. This method overcomes some of the gaps that currently exist in the estimation and product quality assessment of forest carbon density. Other methods are nonparametric estimation approaches, such as k-Nearest Neighbors [
9,
21,
22] examining the distances of each pixel to be estimated to all sample plots in terms of a multi-spectral space and identifying k nearest sample plots and then calculating and assigning a weighted average to the estimated pixel. In addition, artificial neutral networks [
9] and semi-empirical models [
23] have also been applied to map forest carbon density.
Although these methods are available, mapping and accurate assessment of forest carbon density at multiple spatial resolutions is still a challenging task. First, mapping forest carbon density at local, regional and global scales requires collection of field sample plot data at multiple spatial resolutions, which is money-consuming and labor intensive. Second, widely used images for this purpose have a wide range of spatial resolutions from less than 1 m high resolution GeoEye-2 and Worldview-3 to 30 m medium resolution Landsat and 1000 m coarser resolution Moderate Resolution Imaging Spectroradiometer (MODIS) with square pixels. However, sample plots selected for mapping forest carbon density often have limited sizes with different shapes such as square, rectangle and circle. This leads to the mismatch between image pixels and sample plots in shape, size and location, and different accuracies of forest carbon density estimates [
24,
25]. For example, Réjou-Méchain et al. [
25] used 30 large (8–25 ha) permanent plots to quantify spatial variability of aboveground biomass (AGB) at spatial resolutions of 5 to 250 m (0.025—6.25 ha) and found that the spatial sampling error was large for standard plot sizes, averaging 46.3% for 0.1 ha plots and 16.6% for 1 ha plots. The inconsistency and mismatch between image pixels and sample plots will lead to the difficulty to combine the spatial data [
26,
27]. Thus, how to develop a method for collection of sample plot data and mapping of forest carbon density at multiple spatial resolutions becomes critical.
An alternative solution for the inconsistency of image pixels with sample plots in size is scaling up or aggregating spatial data from a finer spatial resolution to a coarser one [
11,
20,
26,
27]. Several authors have summarized the up-scaling methods [
28,
29,
30,
31], including use of nearest neighbor, window or block averaging, data fusion, texture measures, block cokriging, etc. For example, Fu et al. [
11] estimated landscape net ecosystem exchange based on Landsat data using an improved upscaling framework. Another example is that Asner et al. [
32] developed a top-down approach for high-resolution carbon mapping and scaling up to a large region in the Colombian Amazon by employing a universal approach to airborne LiDAR-calibration with limited field data, quantifying environmental controls over carbon densities, and developing stratification- and regression-based approaches. Moreover, in the study of Guitet et al. [
33] spatial variation of AGB at various scales was analyzed using two large forest inventories conducted in French Guiana and the accuracy of estimating AGB increased by 13% from the plot scale to a 2-km spatial resolution. In addition, Bastin et al. [
34] employed fine spatial resolution Geoeye-1 and QuickBird-2 images and harmonizing Fourier textural ordination to detect forest canopy structural heterogeneity in Central Africa and further developed piecewise biomass inversion models using 26 inventory plots (1 ha) to predict AGB variations. However, these methods lack the capacity of modeling propagation of input uncertainties from a finer spatial resolution to a coarser one and of generating spatial distributions of up-scaled estimates and their uncertainties. For this purpose, Wang et al. [
27] developed a spatial variability-based sequential Gaussian block co-simulation (SGBCS) algorithm in which both spatial data and their uncertainties can be scaled up from a finer spatial resolution to any coarser ones, leading to maps of estimates and their uncertainties at coarser spatial resolutions. This method has been applied to mapping and spatial uncertainty analysis of forest carbon density [
20,
31].
On the other hand, the accuracy of forest carbon density maps is often assessed using root mean square error (RMSE) between estimated and observed values [
35,
36]. There have been three methods for obtaining these field observations. First, a set of sample plots is often randomly divided into two sub-sets. One sub-set of data is applied for model development and another for validation of obtained models. This method is limited due to the sample plots used for accuracy assessment are not independent from those used for model development. Secondly, cross-validation can be used for accuracy assessment [
37,
38]. This method greatly saves time and money for collection of field plot data, but means an intensive computation. The best way for accuracy assessment is the acquisition and application of independent sample plots, but this is time- and money-consuming. Additionally, a spatial uncertainty and error budget method can be used [
20,
27,
31,
39,
40,
41]. In this method, various sources of errors are identified, quantified and linked with the output uncertainties, and the contributions of various input errors to the output uncertainties are then calculated. However, this method is relatively complicated. Generally, the accuracy assessment of forest carbon density estimates requires consistent spatial resolutions between the derived forest carbon density maps and sample plot data. When the spatial resolutions are inconsistent, or multiple spatial resolution maps of forest carbon density have to be derived, the accuracy assessment will become a great challenge [
27]. Thus far there have been some studies reported in this area [
11,
20,
27,
31,
32,
33,
34,
35]. However, further study is still needed toward the development of an effective sampling design and an algorithm that can be used to map forest carbon density and conduct accuracy assessment at multiple spatial resolutions.
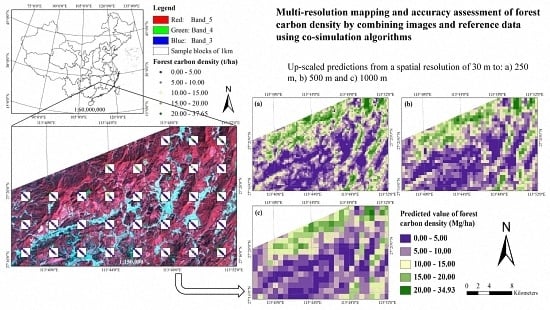
The purpose of this study was to develop a methodological framework for mapping and accuracy assessment of forest carbon density at four spatial resolutions by combining images from Landsat 8 and MODIS and four reference datasets from a systematical, nested and clustering sampling design. This study was carried out in Huang-Feng-Qiao forest farm of You County in Hunan of China. The used images had four spatial resolutions of 30 m × 30 m, 250 m × 250 m, 500 m × 500 m and 1000 m × 1000 m. An image-based sequential Gaussian co-simulation algorithm (SGCS) and SGBCS approach developed by Wang et al. [
20,
27,
31] were employed to map forest carbon density at the spatial resolutions. Moreover, this study compared the accuracies of up-scaled estimates derived by scaling up a SGCS and Landsat derived 30 m resolution map with a window average (WA) (called SGCSWA algorithm), combining Landsat 8 and SGBCS, and combining MODIS images and SGCS, and demonstrated the potential of the methodology to provide the spatial information of forest carbon density at multiple spatial resolutions.
4. Discussion
Multi-resolution mapping and accuracy assessment of forest carbon density require the availability of field observations at the corresponding spatial resolutions, which will lead to a great cost. Usually, remotely sensed data are available at multiple spatial resolutions, while field observations are collected using limited and fixed sizes of sample plots. The inconsistency of spatial resolutions between sample plot and remotely sensed data will result in a great challenge for mapping and accuracy assessment of forest carbon density [
11,
20,
27,
31,
32,
33,
34,
35]. There have only been few relevant studies reported in this field. For this purpose, in this study, a methodological framework was proposed and tested by developing a systematical, nested and clustering sampling design to collect reference data, then generating maps of forest carbon density and conducting accuracy assessment of the maps at four spatial resolutions for Huang-Feng-Qiao forest farm of You County in Eastern Hunan of China. In the sampling design, the used sample plots had a size of 30 m × 30 m. A systematical and equal sampling distance was used to select the 250 m and 500 m sub-blocks and 1000 m blocks. The 30 m sample plots, and 250 m and 500 m sub-blocks were nested within the 1000 m blocks. The sample plots that formed clusters were systematically and consistently allocated along the diagonal lines of the sub-blocks and blocks with unequal, but fixed distances. There were several reasons for using this sampling design. First, most national forest inventories, for example, the national forest inventory in China, use systematical sampling designs and thus the developed methodology can be directly applied to generate forest carbon density maps with the existing national forest inventory sample plots. Second, the four used spatial resolutions: 30 m × 30 m, 250 m × 250 m, 500 m × 500 m and 1000 m × 1000 m match the pixel sizes of the widely used Landsat image and three MODIS products respectively. Third, a certain number of sample plots instead of all of the sample units within the sub-blocks and blocks were selected and measured to make reference of forest biomass and carbon density at the sub-block and block levels to reduce the cost of collecting field plot data. Moreover, a random sampling is not widely used for national forest inventory. In addition, a double and systematical sampling based on stratification and combined with nested sub-blocks with clusters of sample plots may be more efficient, but much more complicated and thus more difficult to use compared to this sampling design.
In addition to the 30 m spatial resolution sample plots, this multi-resolution sampling design led to three, five and seven sample plots for each of the 250 m sub-blocks, 500 m sub-blocks and 1000 m blocks to capture the variation of forest carbon density, respectively. To save time and reduce cost, not all of the 30 m sample plots were measured within each of the sub-blocks and blocks. Instead, three, five and seven sample plots were selected and measured, and an average value from the sample plots was utilized to make the reference of forest carbon density for each of the 250 m sub-blocks, 500 m sub-blocks and 1000 m blocks. This would have resulted in uncertainties of forest carbon density values at the sub-block and block levels. However, this study focused on proposing an idea and developing a methodological framework for multi-resolution mapping and accuracy assessment of forest carbon density and thus, using the numbers of the sample plots would not affect the conclusions of this study. Whether the numbers of sample plots selected at the sub-block and block levels are enough and optimal should be further analyzed in the further studies. In fact, the optimal number of sample plots for each of the coarse spatial resolutions may vary depending on the complexity of forest ecosystems and geographic features [
50].
This study area had a complicated and fragmented forest landscape where various mixed forests, scattered bamboo forests and shrubs, and agricultural lands exist. A relatively large CV (106%) of forest carbon density was obtained from the 30 m spatial resolution sample plots. As expected, the CV greatly decreased from the plot level to the sub-block and block levels. The results of this study showed that although all of the means of the predicted values and maps fell in the confidence intervals of the reference data at the corresponding spatial resolutions, the obtained forest carbon density maps had a larger value (34%)of relative RMSE at the 30 m resolution plot level compared to the previous studies [
11,
20,
32,
34]. For example, Bastin et al. [
34] combined fine spatial resolution satellite images, harmonizing Fourier textural ordination and piecewise biomass inversion models based on 26 inventory plots (1 ha) to predict AGB in Central Africa. They obtained an accuracy of residual standard error (RSE) 15% for forest AGB predictions at the spatial resolution of 100 m × 100 m across a wide range of 26 Mg/ha to 460 Mg/ha by cross validation. Moreover, Asner et al. [
32] used a top-down approach to scale up high spatial resolution carbon estimates to a large region of 16.5 million ha in the Colombian Amazon. They yielded an uncertainty of 14% for LiDAR-derived carbon maps at 1 ha resolution and an uncertainty of 28% for the regional map based on stratification. Compared to those in the studies of Bastin et al. [
34] and Asner et al. [
32], however, in this study the used sample plots and map units were smaller, while the spatial resolution of the used Landsat image was coarser. In addition, other reasons may include more complicated and fragmented forest landscape, the larger CV and neglecting environmental variables and stratification of the landscape. This implied that considering environmental variables and stratification of landscapes and using finer spatial resolution images may provide the potential of increasing the accuracy of mapping forest carbon density. On the other hand, in this study, the accuracy of forest carbon density at the plot level was only slightly lower than that (28%) from the study of Guitet et al. [
33] at the similar plot scale, but much higher than that (53%) for the use of Landsat imagery by Fu et al. [
11] in which an upscaling method that combines footprint climatology modeling, modified regression tree and image fusion was utilized to estimate net ecosystem exchange.
In this study, when the 30 m spatial resolution Landsat 8 image and sample plot data were scaled up to the pixel sizes of 250 m × 250 m, 500 m × 500 m and 1000 m × 1000 m using both algorithm SGCSWA and SGBCS, the obtained relative RMSEs of forest carbon density estimates varied from 5.45% to 5.92%. At the corresponding spatial resolutions the combinations of MODIS products and the reference data led to a range of relative RMSEs from 6.38% to 6.70%. The accuracies at the sub-block and block levels were much higher than that at the plot level mainly because of the smoothing of spatial data and consideration of the features of clustering sampling. The accuracies were also much higher than those (53% vs. 46% for Landsat and MODIS imagery, respectively) from the study of Fu et al. [
11]. Compared to the previous reports [
11,
32,
33,
34], this study has an advantage. That is, a multi-resolution sampling design was developed and from which multi-resolution reference datasets that match the spatial resolutions of the most widely used Landsat and MODIS images were obtained and can be used to conduct mapping and accuracy assessment of forest carbon density. Moreover, the algorithms can scale up both spatial data and input uncertainties and generate the maps of estimates and their uncertainties at coarser spatial resolutions. However, the algorithms require intensive computation for very large areas. This limitation has become less critical as computer science develops. In addition, in this study, only 3–7 30 m spatial resolution sample plots (not all of the sample units) were measured within each of the sub-blocks and blocks, which may have resulted in uncertainties of forest carbon density predictions. Readers should take caution for use of the results and further studies are needed.
This study also showed that the combination of Landsat 8 image and the algorithm SGCSWA resulted in the greatest accuracies of the up-scaled maps, then the combination of Landsat 8 image and SGBCS, and the combinations of the MODIS images and SGCS had lowest accuracies. The reason is mainly because the medium spatial resolution Landsat 8 image provides more detailed information of forest carbon density than the coarser spatial resolution MODIS products. Both algorithms SGCSWA and SGBCS can combine and scale up the 30 spatial resolution sample plot and image data to produce any coarser spatial resolution forest carbon density maps and eliminate the requirement of collecting plot data at the coarser spatial resolutions. Instead of MODIS images, thus, the medium spatial resolution Landsat image with both up-scaling algorithms SGCSWA and SGBCS is recommended for mapping and accuracy assessment of forest carbon density at the coarser spatial resolutions.
It has to be pointed out that in this study, we calculated many band ratios, vegetation indices and texture measures to capture the forest canopy structures and spatial heterogeneity and reduce the effects of slope due to mountainous areas. However, in these algorithms (SGCSWA and SGBCS), only the spectral variable that had the greatest correlation with forest carbon density for each of the spatial resolutions was utilized. The spatial variability of forest carbon density was thus limitedly explained, which may also have increased the uncertainty of predicted values. In future studies, especially when these algorithms are applied to mapping forest carbon density of complicated rainforests, more spectral variables should be used to conduct the co-simulations. This will require a spatial joint multivariate co-simulation algorithm. This method is more complicated and will double the computation and labor costs [
51]. However, the development of computer science will release this limitation.
Finally, in this study, we explored the mapping of forest carbon density at the spatial resolutions of 30 m, 250 m, 500 m and 1000 m instead of other spatial resolutions such as 90 m. There were three reasons for selecting these four spatial resolutions. First, the spatial resolutions exactly match the pixel sizes of Landsat 8 image and three MODIS products that are widely used to map forest carbon density at local, regional, national and global scales. Second, Wang et al. [
27] conducted the up-scaling of spatial data from a spatial resolution of 30 m × 30 m to 90 m × 90 m for mapping vegetation cover using the SGBCS and testified the success of this up-scaling algorithm. Moreover, the purpose of this study was to demonstrate the development of a general methodological framework for mapping forest carbon density at multiple spatial resolutions and the obtained conclusions would be thus generalized.
5. Conclusions
This study focused on the development and assessment of a methodology to conduct mapping and accuracy assessment of forest carbon density at four spatial resolutions by combining Landsat 8 and MODIS images with reference values from sample plots obtained using a multiple resolution, systematical, nested and clustering sampling design. As expected, the results of applying the methodology to the study area showed that all of the means of predicted forest carbon density values at the spatial resolutions of 30 m × 30 m, 250 m × 250 m, 500 m × 500 m and 1000 m × 1000 m fell in the confidence intervals of reference data at a significance level of 0.05. Moreover, with the same reference datasets, images, and the methods, as the spatial resolutions became coarser, the accuracy of the up-scaled predictions decreased and the maps became smoothed. More important is that this study led to four new conclusions. First, the systematical, nested and clustering sampling design provided the potential to obtain spatial information of forest carbon density at multiple spatial resolutions. Second, the relative RMSEs of predicted values at the plot level were much greater than those at the sub-block and block levels. Moreover, the accuracies of the up-scaled estimates were much higher than those from previous studies. In addition, at the same spatial resolution, SGCSWA resulted in smallest relative RMSEs of the up-scaled predictions, then the combinations of Landsat image and SGBCS, and the accuracies from both methods were significantly greater than those from the combinations of the MODIS images and SGCS. Overall, this study implied that the combinations of Landsat 8 image and SGCSWA or SGBCS with the systematical, nested and clustering sampling design provided the potential to formulate a methodological framework to map forest carbon density and conduct accuracy assessment at multiple spatial resolutions. However, this methodology needs to be further refined and examined in other forest landscapes.