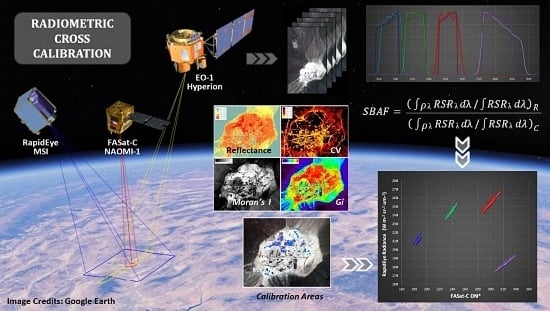
Radiometric Cross-Calibration of the Chilean Satellite FASat-C Using RapidEye and EO-1 Hyperion Data and a Simultaneous Nadir Overpass Approach
Abstract
:1. Introduction
2. Background on the Calibration of Satellite Sensors
2.1. Absolute Radiometric Calibration and Approaches
2.2. Compensation Factors
3. Study Area and Satellite Data
3.1. Frenchman Flat Calibration Site
3.2. Overview of Sensors and Satellite Data
4. Methods
4.1. Spatial Autocorrelation and Uniformity Analysis
4.2. Sample Extraction
4.3. E0 Calculation for FASat-C
4.4. Compensation Factors
4.5. Cross-Calibration of FASat-C NAOMI-1
5. Results
5.1. Spatial Analysis of the Calibration Site
5.2. E0 and Compensation Factors
5.3. Radiometric Cross-Calibration
5.4. Preliminary Evaluation Results
5.4.1. Per-Band Bias Errors
5.4.2. Per-Band Absolute Error
6. Discussion
7. Conclusions and Further Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| APEX | Airborne Prism Experiment |
| BRDF | Bi-directional Reflectance Distribution Function |
| Cal | Calibration Samples |
| Cal/Val | Calibration and Validation |
| CEOS | Committee on Earth Observation Satellites |
| CV | Coefficient of Variation |
| DN | Digital Numbers |
| ETM+ | Enhanced Thematic Mapper Plus |
| EO-1 | Earth Observing-1 Mission |
| Eva | Evaluation Samples |
| FASat-C | Air Force Satellite-C |
| FWHM | Full Width at Half Maximum |
| GaoFen-1 | Chinese High Resolution Imaging Satellite-1 |
| GOE | Space Operations Group |
| GSD | Ground Sampling Distance |
| HDF | Hierarchical Data Format |
| HSI | Hyperspectral Imager |
| L8-OLI | Landsat-8 Operational Land Imager |
| LISA | Local Indicators of Spatial Association |
| LSpec | LED-Based Spectral Surface Monitoring Calibration Site |
| MAPE | Mean Absolute Percentage Error |
| m.a.s.l. | meters above sea level |
| MBE | Mean Bias Error |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| MODTRAN | Moderate Resolution Atmospheric Transmission |
| MSI | Multispectral Imager |
| NAOMI-1 | New AstroSat Optical Modular Instrument |
| NASA | National Aeronautics Space Agency |
| OBC | On–Board Calibrator |
| PICS | Pseudo-Invariant Calibration Sites |
| RMSE | Root Mean Square Error |
| RSR | Relative Spectral Response |
| SAF | Aerial Photogrammetric Service |
| SBAF | Spectral Band Adjustment Factor |
| SCIAMACHY | Scanning Imaging Absorption Spectrometer for Atmospheric Cartography |
| SNO | Simultaneous Nadir Overpass |
| SNR | Signal-to-Noise Ratio |
| SRF | Spectral Response Function |
| SSOT | Sistema Satelital de Observación de la Tierra |
| TERRA-ASTER | Advanced Spaceborne Thermal Emission and Reflection Radiometer |
| TOA | Top-of-Atmosphere |
| UTM | Universal Transversal Mercator |
| VIS/NIR | Visible Near Infrared |
| WGCV | Working Group on Calibration and Validation |
| WGS84 | World Geodetic System 1984 |
References
- Slater, P.N.; Biggar, S.F.; Helm, R.G.; Jackson, R.D.; Mao, Y.; Moran, M.S.; Palmer, J.M.; Yuan, B. Reflectance- and radiance-based methods for the in-flight absolute calibration of multispectral sensors. Remote Sens. Environ. 1987, 22, 11–37. [Google Scholar] [CrossRef]
- Trishchenko, A.P.; Cihlar, J.; Li, Z. Effects of spectral response function on surface reflectance and NDVI measured with moderate resolution satellite sensors. Remote Sens. Environ. 2002, 81, 1–18. [Google Scholar] [CrossRef]
- Ponzoni, F.; Zullo, J.; Lamparelli, R.; Pellegrino, G.; Arnaud, Y. In-flight Absolute Calibration of the Landsat-5 TM on the Test Site Salar Uyuni. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2761–2766. [Google Scholar] [CrossRef]
- Teillet, P.; Barsi, J.; Chander, G.; Thome, K. Prime candidate earth targets for the post-launch radiometric calibration of space-based optical imaging instruments. Proc. SPIE 2007. [Google Scholar] [CrossRef]
- Cao, C.; Chen, R.; Uprety, S. Calibrating a System of Satellite Instruments. In Satellite-Based Applications on Climate Change; Qu, J., Powell, A., Sivakumar, M.V.K., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 13–29. [Google Scholar]
- Gürbüz, S.; Özen, H.; Chander, G. A survey of LANDNET sites focusing on Tuz Gölü salt lake, Turkey. In Proceedings of the XXII ISPRS Congress, Melbourne, Australia, 25 August–1 September 2012; pp. 115–120.
- Markham, B.; Helder, D. Forty-year calibrated record of earth-reflected radiance from Landsat: A review. Remote Sens. Environ. 2012, 122, 30–40. [Google Scholar] [CrossRef]
- Chander, G.; Helder, D.; Aaron, D.; Mishra, N.; Shrestha, A. Assessment of Spectral, Misregistration and Spatial Uncertainties Inherent in the Cross–Calibration Study. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1282–1296. [Google Scholar] [CrossRef]
- Mattar, C.; Hernández, J.; Santamaría-Artigas, A.; Durán-Alarcón, C.; Olivera, L.; Inzunza, M.; Tapia, D.; Escobar-Lavín, E. A first in-flight absolute calibration of the Chilean Earth Observation Satellite. ISPRS J. Photogramm. Remote Sens. 2014, 92, 16–25. [Google Scholar] [CrossRef]
- Servicio Aerofotogramétrico de la FACH. 2013. FASat-C User Guide. Available online: http://www.saf.cl (accessed on 6 January 2016).
- Latorre, C.; Camacho, F.; Mattar, C.; Santamaría-Artigas, A.; Leiva-Büchi, N.; Lacaze, R. Obtención de mapas de alta resolución de LAI, FAPAR y fracción de cobertura vegetal derivados de imágenes del satélite chileno FASat-C y adquisiciones in-situ en la zona agrícola de Chimbarongo, Chile. In Proceedings of the XVI Congreso de la Asociación Española de Teledetección, Sevilla, Spain, 21–23 October 2015; pp. 104–107.
- Santamaría-Artigas, A.; Mattar, C.; Durán-Alarcón, C.; Olivera, L.; Inzunza, M.; Tapia, D.; Escobar-Lavín, E. Primera aplicación de imágenes FASat-Charlie al estudio de praderas semi-áridas de Chile. Rev. Teledetec. 2013, 40, 78–87. [Google Scholar]
- Rao, C.R.; Chen, J.; Sullivan, J.T.; Zhang, N. Post-launch calibration of meteorological satellite sensors. Adv. Space Res. 1999, 23, 1357–1365. [Google Scholar] [CrossRef]
- Wang, D. Satellite Data Degradation and Their Impacts on High-Level Products. In Remotely Sensed Data Characterization, Classification, and Accuracies; Thenkabail, P.S., Ed.; Remote Sensing Handbook; CRC Press: Boca Raton, FL, USA, 2015; Volume I, pp. 143–152. [Google Scholar]
- Cao, C.; Weinreb, M.; Xu, H. Predicting simultaneous nadir overpasses among polar-orbiting meteorological satellites for the inter-satellite calibration of radiometers. J. Atmos. Ocean. Technol. 2004, 21, 537–542. [Google Scholar] [CrossRef]
- Cao, C.; Ciren, P.; Goldberg, M.; Weng, F.; Zou, C. Simultaneous Nadir Overpasses for NOAA-6 to NOAA-17 Satellites from 1980 to 2003 for the Inter-Satellite Calibration of Radiometers; NOAA Technical Report NESDIS 118; NOAA: College Park, MD, USA, 2005; p. 74.
- Heidinger, A.K.; Cao, C.; Sullivan, J.T. Using Moderate Resolution Imaging Spectrometer (MODIS) to calibrate advance very high resolution radiometer reflectance channels. J. Geophys. Res. Atmos. 2002, 107, 4702–4704. [Google Scholar] [CrossRef]
- Qi, C.; Chen, Y.; Liu, H.; Wu, C.; Yin, D. Calibration and validation of the InfraRed atmospheric sounder onboard the FY3B satellite. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4903–4914. [Google Scholar] [CrossRef]
- Teillet, P.; Barker, J.; Markham, B.; Irish, R.; Fedosejevs, G.; Storey, J. Radiometric cross calibration of the Landsat-7 ETM+ and Landsat-5 TM sensors based on tandem data sets. Remote Sens. Environ. 2001, 78, 39–54. [Google Scholar] [CrossRef]
- Teillet, P.M.; Markham, B.L.; Irish, R.R. Landsat Cross–Calibration based on near simultaneous imaging of common ground targets. Remote Sens. Environ. 2006, 102, 264–270. [Google Scholar] [CrossRef]
- Chander, G.; Mishra, N.; Helder, D.; Aaron, D.; Angal, A.; Choi, T.; Xiong, X.; Doelling, D. Applications of Spectral Band Adjustment Factors (SBAF) for cross–calibration. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1267–1281. [Google Scholar] [CrossRef]
- Bedingfield, K.L.; Leach, R.D. Spacecraft System Failures and Anomalies Attributed to the Natural Space Environment; Alexander, M.B., Ed.; NASA Reference Publication 1390; NASA: Huntsville, AL, USA, 1996.
- Wang, D.; Morton, D.; Masek, J.; Wu, A.S.; Nagol, J.; Xiong, X.X.; Levy, R.; Vermote, E.; Wolfe, R. Impact of sensor degradation on the MODIS NDVI time series. Remote Sens. Environ. 2012, 119, 55–61. [Google Scholar] [CrossRef]
- Guenther, B. VIIRS on-orbit spectral throughput degradation: a physical model with specific guidance on handling sensor characteristics for EDR development. In Proceedings of the 21st Annual Conference on Characterization and Radiometric Calibration for Remote Sensing, (CALCON), Logan, UT, USA, 27–30 August 2012.
- Tribble, A.C.; Gorney, D.J.; Blake, J.B.; Koons, H.C.; Schulz, M.; Vampola, A.L.; Walterscheid, R.L.; Wertz, J.R. The Space Environment and Survivability. In Space Mission Analysis and Design, 3rd ed.; Larson, W., Wertz, J., Eds.; Space Technology Library, Microcosm Press and Kluwer Academic Publishers: El Segundo, CA, USA; Dordrecht, The Netherlands, 2005; pp. 203–240. [Google Scholar]
- Barker, J.L. Relative radiometric calibration of Landsat TM reflective bands. In Proceedings of the Landsat-4 Science Characterization Early Results, Greenbelt, MD, USA, 22–24 February 1983; Volume 3.
- Johnson, B.C.; Brown, S.W.; Price, J.P. Metrology for Remote Sensing Radiometry. In Post-Launch Calibration of Satellite Sensors; Morain, S., Budge, A., Eds.; Taylor & Francis Group: London, UK, 2004; pp. 7–16. [Google Scholar]
- Meckler, Y.; Kauffman, Y. Possible causes of calibration degradation of the Advanced Very High Resolution Radiometer visible and near-infrared channels. Appl. Opt. 1995, 34, 1059–1062. [Google Scholar] [CrossRef] [PubMed]
- Barnes, R.A.; Eplee, R.E.; Schmidt, G.M.; Patt, F.S.; Mc Clain, C.R. Calibration of SeaWiFS: Direct techniques. Appl. Opt. 2001, 40, 6682–6700. [Google Scholar] [CrossRef] [PubMed]
- Tansock, J.; Bancroft, D.; Butler, J.; Cao, C.; Datla, R.; Hansen, S.; Helder, D.; Kacker, R.; Latvakoski, H.; Mlynczak, M.; et al. Guidelines for Radiometric Calibration of Electro-Optical Instruments for Remote Sensing; National Institute of Standards and Technology and U.S. Department of Commerce: Washington, DC, USA, 2015. [CrossRef]
- CEOS Cal/Val Portal. Available online: http://calvalportal.ceos.org/ (accessed on 5 February 2016).
- Chander, G.; Hewison, T.J.; Fox, N.P.; Wu, X.Q.; Xiong, X.X.; Blackwell, W.J. Overview of intercalibration of satellite instruments. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1056–1080. [Google Scholar] [CrossRef]
- Dinguirard, M.; Slater, P. Calibration of space-multispectral imaging. Remote Sens. Environ. 1999, 68, 194–205. [Google Scholar] [CrossRef]
- Thome, K.J. Absolute radiometric calibration of Landsat 7 ETM+ using the reflectance- based method. Remote Sens. Environ. 2001, 78, 27–38. [Google Scholar] [CrossRef]
- Slater, P.; Biggar, S. Suggestions for radiometric calibration coefficients generation. J. Atmos. Ocean. Technol. 1996, 13, 386–382. [Google Scholar] [CrossRef]
- Santer, R.; Gu, X.F.; Guyot, G.; Deuzé, J.L.; Devaux, C.; Vermote, E.; Verbrugghe, M. SPOT calibration at the La Crau test site (France). Remote Sens. Environ. 1992, 41, 227–237. [Google Scholar] [CrossRef]
- Hovis, W.; Knoll, J.; Smith, G. Aircraft measurements for calibration of an orbiting spacecraft sensor. Appl. Opt. 1985, 24, 407–410. [Google Scholar] [CrossRef] [PubMed]
- Biggar, S.; Santer, R.; Slater, P. Irradiance-based Calibration of Imaging Sensors. In Proceedings of the 10th Annual International Geoscience and Remote Sensing Symposium, IGARSS’90, College Park, MD, USA, 20–24 May 1990; pp. 507–510.
- Vermote, E.; Kaufman, Y.J. Absolute calibration of AVHRR visible and infrared channels using ocean and cloud views. Int. J. Remote Sens. 1995, 16, 2317–2340. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Holben, B.N. Calibration of the AVHRR visible and near-IR bands by atmospheric scattering, ocean glint and desert reflection. Int. J. Remote Sens. 1993, 14, 21–52. [Google Scholar] [CrossRef]
- Fougnie, B.; Llido, J.; Gross-Colzy, L.; Henry, P.; Blumstein, D. Climatology of oceanic zones for in-flight calibration. Proc. SPIE 2010. [Google Scholar] [CrossRef]
- Doelling, D.R.; Nguyen, L.; Minnis, P. On the use of deep convective clouds to calibrate AVHRR data. Proc. SPIE 2004. [Google Scholar] [CrossRef]
- Doelling, D.R.; Morstad, D.; Scarino, B.R.; Bhatt, R.; Gopalan, A. the characterization of deep convective clouds as an invariant calibration target and as a visible calibration technique. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1147–1159. [Google Scholar] [CrossRef]
- Cosnefroy, H.; Leroy, M.; Briottet, X. Selection and Characterization of Saharan and Arabian Desert Sites for the Calibration of Optical Satellite Sensors. Remote Sens. Environ. 1996, 58, 101–114. [Google Scholar] [CrossRef]
- Henry, P.; Dinguirard, M.; Bodilis, M. SPOT multitemporal calibration over stable desert areas. In Proceedings of the EUROPTO /SPIE, Orlando, FL, USA, 15 November 1993; Volume 1938, pp. 67–76.
- Kieffer, H.H.; Wildey, R.L. Establishing the moon as a spectral radiance standard. J. Atmos. Ocean. Technol. 1996, 13, 360–375. [Google Scholar] [CrossRef]
- Stone, T.; Kieffer, H.; Becker, K. Modelling the radiance of moon for on-orbit calibration. Proc. SPIE 2003. [Google Scholar] [CrossRef]
- Bowen, H.S. Absolute Radiometric Calibration of the IKONOS Sensor Using Radiometrically Characterized Stellar Sources. In Proceedings of the PECORA 15, Land Satellite Information IV, ISPRS Commission I Symposium, Denver, CO, USA, 10–15 November 2002.
- Bowen, H.S.; Cunningham, D.M. Correction to Method of Establishing the Absolute Radiometric Accuracy of Remote Sensing Systems While On-orbit Using Characterized Stellar Sources. In Proceedings of the JACIE, Reston, VA, USA, 15 March 2006.
- Fourest, S.; Lebegue, L.; Dechoz, C.; Lachérade, S.; Blanchet, G. Star-based methods for Pleiades-HR commissioning. In Proceedings of the XXII ISPRS Congress, Melbourne, Australia, 25 August–1 September 2012; pp. 531–536.
- Czapla-Myers, J.; McCorkel, J.; Anderson, N.; Thome, K.; Biggar, S.; Helder, D.; Aaron, D.; Leigh, L.; Mishra, N. The ground-based absolute radiometric calibration of Landsat 8 OLI. Remote Sens. 2015, 7, 600–626. [Google Scholar] [CrossRef]
- Vermote, E.; Saleous, N.Z. Calibration of NOAA 16 AVHRR over a desert site using MODIS data. Remote Sens. Environ. 2007, 105, 214–220. [Google Scholar] [CrossRef]
- Lachérade, S.; Fougnie, B.; Henry, P.; Gamet, P. Cross calibration over desert sites: Description, methodology and operational implementation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1098–1113. [Google Scholar] [CrossRef]
- Mishra, N.; Haque, M.O.; Leigh, L.; Aaron, D.; Helder, D.; Markham, B. Radiometric cross calibration of Landsat 8 Operational Land Imager (OLI) and Landsat 7 Enhanced Thematic Mapper Plus (ETM+). Remote Sens. 2014, 6, 12619–12638. [Google Scholar] [CrossRef]
- Liu, J.J.; Li, Z.; Qiao, Y.L.; Liu, Y.J.; Zhang, Y.X. A new method for cross–calibration of two satellite sensors. Int. J. Remote Sens. 2004, 23, 5267–5281. [Google Scholar] [CrossRef]
- Feng, L.; Li, J.; Gong, W.; Zhao, X.; Chen, X.; Pang, X. Radiometric cross–calibration of Gaofen-1 WFV cameras using Landsat–8 OLI images: A solution for large view angle associated problems. Remote Sens. Environ. 2016, 174, 56–68. [Google Scholar] [CrossRef]
- Gil, J.; Romo, A.; Moclán, C.; Pirondini, F. Deimos‒2 Post-launch radiometric calibration. In Proceedings of JACIE, Tampa, FL, USA, 5–7 May 2015.
- Gao, H.; Gu, X.; Yu, T.; Liu, L.; Sun, Y.; Xie, Y.; Liu, Q. Validation of the calibration coefficient of the GaoFen–1 PMS sensor using the Landsat–8 OLI. Remote Sens. 2016, 8, 132. [Google Scholar] [CrossRef]
- Lachérade, S.; Fourest, S.; Gamet, P.; Lebègue, L. Pleiades absolute calibration: in-flight calibration sites and methodology. In Proceedings of the XXII ISPRS Congress, Melbourne, Australia, 25 August–1 September 2012; pp. 549–554.
- Chander, G.; Markham, B.L.; Barsi, J. Revised Landsat-5 Thematic Mapper radiometric calibration. IEEE Geosci. Remote Sens. Lett. 2007, 4, 490–494. [Google Scholar] [CrossRef]
- Henry, P.; Chander, G.; Fougnie, B.; Thomas, C.; Xiong, X. Assessment of spectral band impact on intercalibration over desert sites using simulation based on EO-1 Hyperion data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1297–1308. [Google Scholar] [CrossRef]
- Teillet, P.; Fedosejevs, G.; Thome, K.; Barker, J. Impacts of spectral band difference effects on radiometric cross calibration between satellite sensors in the solar- reflective spectral domain. Remote Sens. Environ. 2007, 110, 393–409. [Google Scholar] [CrossRef]
- Trishchenko, A.P.; Cihlar, J.; Li, Z.Q.; Hwang, B. Long-term monitoring of surface reflectance, NDVI and clouds from space: What contribution we can expect due to effect of instrument spectral response variations? In Proceedings of the SPIE 4815, Atmospheric Radiation Measurements and Applications in Climate, Seattle, WA, USA, 9 September 2002. [CrossRef]
- Doelling, D.R.; Lukashin, C.; Minnis, P.; Scarino, B.; Morstad, D. Spectral Reflectance Corrections for Satellite Intercalibrations Using SCIAMACHY Data. IEEE Geosci. Remote Sens. Lett. 2012, 9, 119–123. [Google Scholar] [CrossRef]
- D’Odorico, P.; Gonsamo, A.; Damm, A.; Schaepman, M. Experimental Evaluation of Sentinel-2 Spectral Response Functions for NDVI Time-Series Continuity. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1336–1348. [Google Scholar] [CrossRef]
- Gonsamo, A.; Chen, J. Spectral Response Function Comparability among 21 Satellite Sensors for Vegetation Monitoring. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1319–1335. [Google Scholar] [CrossRef]
- Cundill, S.; van der Werff, H.; van der Meijde, M. Adjusting Spectral Indices for Spectral Response Function Differences of Very High Spatial Resolution Sensors Simulated from Field Spectra. Sensors 2015, 15, 6221–6240. [Google Scholar] [CrossRef] [PubMed]
- Allred, D.M.; Beck, D.E.; Jorgensen, C.D. Biotic communities of the Nevada Test Site. Brigham Young Univ. Sci. Bull. Biol. Ser. 1963, 2, 1–18. [Google Scholar]
- U.S. Energy Research and Development Administration. Final Environmental Impact Statement; ERDA-1551; Nevada Test Site: Nye County, NV, USA, 1977.
- Scott, K.P.; Thome, K.J.; Brownlee, M.R. Evaluation of the Railroad Valley Playa for use in vicarious calibration. Proc. SPIE 1996, 2818, 158–166. [Google Scholar]
- Polder, M.; Bruegge, C.; Helminger, M.; Taylor, M. Investigation of the LSpec autonomous ground calibration site using MODIS, Landsat ETM+, and IKONOS. In Proceedings of the JACIE, Fairfax, VA, USA, 18 March 2010.
- Hamm, N.A.S.; Atkinson, P.M.; Milton, E.J. A per-pixel, non-stationary mixed model for empirical line atmospheric correction in remote sensing. Remote Sens. Environ. 2012, 124, 666–678. [Google Scholar] [CrossRef]
- Naughton, D.; Brunn, A.; Czapla-Myers, J.; Douglass, S.; Thiele, M.; Weichelt, H.; Oxfort, M. Absolute radiometric calibration of the RapidEye multispectral imager using the reflectance-based vicarious calibration method. SPIE J. Appl. Remote Sens. 2011, 5. [Google Scholar] [CrossRef]
- Brunn, A.; Naughton, D.; Weichelt, H.; Douglass, S.; Thiele, M.; Oxfort, M.; Beckett, K. The calibration procedure of the multispectral imaging instruments on board the RapidEye remote sensing Satellites. In Proceedings of the International Calibration and Orientation Workshop, EuroCow, Castelldefels, Spain, 10–12 February 2010.
- Thiele, M.; Anderson, C.; Brunn, A. Cross-Calibration of the RapidEye Multispectral Imager Payloads using Pseudo-Invariant Test Sites. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Vol. XXXIX-B1, XXII ISPRS Congress, Melbourne, Australia, 25 August–1 September 2012; pp. 167–171.
- Brunn, A.; Bahloul, S.; Hoffmann, D.; Anderson, A. Recent Progress in In-Flight Radiometric Calibration and Validation of the RapidEye Constellation of 5 Multispectral Remote Sensing Satellites; Fay, H., Akihiro, S., Eds.; Image and Video Technology—PSIVT 2015 Workshops; Springer: Auckland, New Zealand; Volume 9555, pp. 273–284.
- Brunn, A.; Blackbridge AG, Calibration & Validation, Brandenburg an der Havel, Germany. Personal communication, 2016.
- Anderson, C.; Brunn, A.; Thiele, M. Absolute Calibration of the RapidEye Constellation. In Proceedings of the 23rd the Annual Conference on Characterization and Radiometric Calibration for Remote Sensing, (CALCON), Logan, UT, USA, 11–14 August 2014.
- Folkman, M.; Pearlman, J.; Liao, L.; Jarecke, P. EO-1/Hyperion hyperspectral imager design, development, characterization and calibration. Proc. SPIE 2001. [Google Scholar] [CrossRef]
- Earth Explorer NASA. Available online: http://earthexplorer.usgs.gov (accessed on 5 February 2016).
- Anselin, L. Local Indicators of Spatial Association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The Analysis of Spatial Association by Use of Distance Statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Bannari, A.; Omari, K.; Teillet, P.M.; Fedosejevs, G. Multisensor and multiscale survey and characterization for radiometric spatial uniformity and temporal stability of Railroad Valley Playa (Nevada) test site used for optical sensor calibration. Proc. SPIE 2004, 5234, 590–604. [Google Scholar]
- Bannari, A.; Omari, K.; Teillet, P.M.; Fedosejevs, G. Potential of Getis statistics to characterize the radiometric uniformity and stability of test sites used for calibration of Earth observation sensors. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2918–2925. [Google Scholar] [CrossRef]
- Odongo, V.O.; Hamm, N.A.S.; Milton, E.J. Spatio-Temporal Assessment of Tuz Gölü, Turkey as a Potential Radiometric Vicarious Calibration Site. Remote Sens. 2014, 6, 2494–2513. [Google Scholar] [CrossRef]
- Thome, K.; Biggar, S.; Slater, P. Effects of assumed solar spectral irradiance on intercomparisons of earth-observing sensors. Proc. SPIE 2001, 4540. [Google Scholar] [CrossRef]
- Thuillier, G.; Herse, M.; Labs, S.; Foujols, T.; Peetermans, W.; Gillotay, D.; Simon, P.C.; Mandel, H. The Solar Spectral Irradiance from 200 to 2400 nm as Measured by SOLSPEC Spectrometer from the ATLAS and EURECA Missions. Sol. Phys. 2003, 214, 1–22. [Google Scholar] [CrossRef]
- Sampath, A.; Haque, O.; Chander, G. Radiometric and Geometric Assessment of Data from RapidEye Constellation of Satellites. In Proceedings of the JACIE, Boulder, CO, USA, 28–31 March 2011.
- Chen, W.; Zhao, H.; Li, Z.; Jing, X.; Yan, L. Uncertainty Evaluation of an In-Flight Absolute Radiometric Calibration Using a Statistical Monte Carlo Method. IEEE Trans. Geosci. Remote Sens. 2013, 53, 2925–2934. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lee, J.; Fox, M.; Adler-Golden, S.M.; Chetwynd, J.H.; Hoke, M.L.; et al. MODTRAN5: 2006 Update. Proc. SPIE 2006, 6233. [Google Scholar] [CrossRef]
- Green, R.O. Spectral calibration requirement for Earth-looking imaging spectrometers in the solar-reflected spectrum. Appl. Opt. 1998, 37, 683–690. [Google Scholar] [CrossRef] [PubMed]
- Gao, B.; Montes, M.J.; Davis, J.O. Refinement of wavelength calibrations of hyperspectral imaging data using a spectrum-matching technique. Remote Sens. Environ. 2004, 90, 424–433. [Google Scholar] [CrossRef]
- Cao, C.; Ciren, P. Inflight spectral calibration of HIRS using AIRS observations. In Proceedings of the 13th Conference on Satellite Meteorology and Oceanography, Norfolk, VA, USA, 20–23 September 2004.
- Yu, F.; Wu, X. Correction for GOES Imager Spectral Response Function Using GSICS. Part I: Theory. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1215–1223. [Google Scholar] [CrossRef]
- Yu, F.; Wu, X. 2013. Correction for GOES Imager Spectral Response Function Using GSICS. Part II: Applications. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1200–1213. [Google Scholar] [CrossRef]
- Sohn, B.J.; Kim, B.; Lee, S. Possible shift of spectral response function of the MODIS 6.8 μm water vapor channel causing a cold bias of 2–3 K. Atmos. Meas. Tech. 2010, 3, 1667–1672. [Google Scholar] [CrossRef]
- Willart-Soufflet, V.; Santer, R. Using AVIRIS for in-flight calibration of the spectral shifts of SPOT-HRV and AVHRR. In Proceedings of the 4th Annual JPL Airborne Geoscience Workshop, 25 October 1993; JPL Publ. 93–26. pp. 197–200.
- Pinto, C.T.; Ponzoni, F.J.; Barrientos, C.; Mattar, C.; Santamaría-Artigas, A.; Castro, R.M. Spectral and atmospheric characterization of a surface at Atacama Desert for earth observation sensors calibration. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2227–2231. [Google Scholar] [CrossRef]
- Camacho, F.; Lacaze, R.; Latorre, C.; Baret, F.; de la Cruz, F.; Demarez, V.; di Bella, C.; García-Haro, J.; González-Dugo, M.P.; Kussul, N.; et al. Collection of Ground Biophysical Measurements in support of Copernicus Global Land Product Validation: The ImagineS database. In Proceedings of the EGU General Assembly, Vienna, Austria, 17–22 April 2015. Geophysical Research Abstracts, 17 EGU2015-2209-1.
- Mattar, C.; Santamaría-Artigas, A.; Durán-Alarcón, C.; Olivera-Guerra, L.; Fuster, R.; Borvarán, D. The LAB-Net Soil Moisture Network: Application to Thermal Remote Sensing and Surface Energy Balance. Data 2016, 1, 6. [Google Scholar] [CrossRef]
- Olivera-Guerra, L.; Merlin, O.; Mattar, C.; Durán-Alarcón, C.; Santamaría-Artigas, S.; Stefan, V. Combining meteorological and lysimeter data to evaluate energy and water fluxes over a row crop for remote sensing applications. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015.
- Santamaría-Artigas, A.; Mattar, C.; Wigneron, J.P.; Olivera-Guerra, L.; Durán-Alarcón, C. Calibration and evaluation of an optical-passive microwave approach to estimate soil moisture over several land cover types. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015.
- Santamaría-Artigas, A.; Mattar, C.; Wigneron, J.P. Application of a Combined Optical–Passive Microwave Method to Retrieve Soil Moisture at Regional Scale Over Chile. IEEE J. Sel. Top. Appl. Earth Obs. 2016, 9, 119–123. [Google Scholar] [CrossRef]
- Laboratory for the Analysis of the Biosphere. LAB-Net Sites. Available online: http://biosfera.uchile.cl/LAB-net.html (accessed on 5 February 2016).
- McCorkel, J.; Thome, K.; Lockwood, R.B. Absolute Radiometric Calibration of Narrow-Swath Imaging Sensors With Reference to Non-Coincident Wide-Swath Sensors. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1309–1318. [Google Scholar] [CrossRef]









| Specifications | RapidEye-MSI (RE4) | FASat-C NAOMI-1 |
|---|---|---|
| Orbital height (km) | 630 | 620 |
| Nominal GSD at-nadir (m) | 6.5 | 5.8 |
| Dynamic range (bits) | 12 | 10 |
| Swath (km) | 77 | 10 |
| Descending node | 11:00 a.m. | 10:30 a.m. |
| Spectral Bands (nm) | ||
| Blue | 440–510 | 455–520 |
| Green | 520–590 | 528–588 |
| Red | 630–685 | 625–695 |
| NIR | 760–850 | 758–881 |
| 36.8108° N; 115.9313° W | RapidEye (RE4) | FASat-C |
|---|---|---|
| UTC Time | 19:22 | 18:51 |
| Incidence Angle | 3.760 | 1.237 |
| Sun Azimuth Angle | 158.437 | 138.372 |
| Sun Elevation Angle | 71.912 | 69.070 |
| Satellite Azimuth Angle | 279.570 | 100.084 |
| Satellite View Angle | 3.401 | −1.127 |
| Date | 5 October 2007 | 4 August 2008 | 12 January 2009 | 15 June 2009 | 25 February 2010 | 22 July 2010 | 7 February 2013 |
|---|---|---|---|---|---|---|---|
| UTC Time | 18:14:29 | 18:11:15 | 18:03:01 | 18:08:19 | 18:07:44 | 18:06:15 | 17:56:38 |
| Sun Azimuth Angle | 152.137 | 125.500 | 151.502 | 116.224 | 145.151 | 119.035 | 145.445 |
| Sun Elevation Angle | 44.722 | 60.636 | 26.370 | 65.377 | 37.620 | 61.920 | 30.766 |
| Inclination Angle | 98.10 | 98.09 | 98.20 | 98.10 | 98.19 | 98.08 | 98.12 |
| Satellite View Angle | 12.425 | 5.981 | −9.094 | 0.432 | −0.595 | −3.364 | 6.603 |
| Band | E0 | Illumination | SBAFCal | St Dv SBAFCal | AiCal | SBAFEva | St Dv SBAFEva | AiEva |
|---|---|---|---|---|---|---|---|---|
| B1 | 1975.85 | 1.03172 | 0.96608 | 0.0009 | 0.99672 | 0.97882 | 0.0115 | 1.00987 |
| B2 | 1825.06 | 1.01715 | 0.99860 | 0.0001 | 1.01573 | 0.99971 | 0.0011 | 1.01686 |
| B3 | 1536.95 | 1.02042 | 1.00583 | 0.0003 | 1.02637 | 1.00516 | 0.0010 | 1.02569 |
| B4 | 1027.58 | 1.10630 | 0.97358 | 0.0016 | 1.07707 | 0.97219 | 0.0023 | 1.07553 |
| Band | n | Free Intercept (Fi) | Zero Intercept (I0) | Pre-Flight Calibration (Pre-F) | ||||
|---|---|---|---|---|---|---|---|---|
| Gain | Offset | R2 | Gain | R2 | Gain Pre-F−1 | Δ Gain (I0—Pre-F−1) | ||
| B1 | 127 | 0.9941 | 26.266 | 0.8418 | 1.1357 | 0.8248 | 1.0708 | 5.71% |
| B2 | 125 | 0.9691 | 12.787 | 0.9284 | 1.0230 | 0.9255 | 0.9867 | 3.55% |
| B3 | 128 | 0.8631 | −4.605 | 0.9391 | 0.8476 | 0.9388 | 0.8239 | 2.78% |
| B4 | 129 | 0.5741 | −1.696 | 0.9260 | 0.5688 | 0.9259 | 0.63068 | −10.88% |
| Band | Cal | Radiance | Reflectance | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MBE | St Dv | Median | Max | Min | MBE | St Dv | Median | Max | Min | ||
| B1 | Pre-F | 9.03 | 2.43 | 9.26 | 16.48 | 4.70 | 0.015 | 0.004 | 0.016 | 0.028 | 0.008 |
| I0 | 0.17 | 2.79 | −0.29 | 8.11 | −5.45 | 0.000 | 0.005 | 0.000 | 0.014 | −0.009 | |
| B2 | Pre-F | 7.57 | 3.22 | 8.06 | 17.10 | 1.12 | 0.014 | 0.006 | 0.015 | 0.032 | 0.002 |
| I0 | 1.67 | 2.82 | 1.33 | 8.95 | −5.48 | 0.003 | 0.005 | 0.002 | 0.017 | −0.010 | |
| B3 | Pre-F | 8.17 | 2.22 | 7.91 | 14.73 | 2.45 | 0.018 | 0.005 | 0.018 | 0.033 | 0.005 |
| I0 | 3.36 | 2.27 | 3.51 | 9.80 | −3.30 | 0.007 | 0.005 | 0.008 | 0.022 | −0.007 | |
| B4 | Pre-F | −10.37 | 5.28 | −8.02 | −0.23 | −22.76 | −0.032 | 0.016 | −0.024 | −0.001 | −0.069 |
| I0 | 3.40 | 1.75 | 3.62 | 9.41 | −2.88 | 0.010 | 0.005 | 0.011 | 0.029 | −0.009 | |
| Band | Calibration | RMSE | MAPE | St Dv | Min. | 1st Quartile | Median | 3rd Quartile | Max. |
|---|---|---|---|---|---|---|---|---|---|
| B1 | Pre-F | 6.27% | 6.01% | 1.81% | 3.03% | 4.80% | 5.53% | 7.35% | 13.36% |
| I0 | 1.94% | 1.51% | 1.23% | 0.00% | 0.56% | 1.20% | 2.15% | 8.12% | |
| B2 | Pre-F | 5.00% | 4.61% | 1.93% | 0.79% | 3.29% | 4.26% | 5.88% | 13.10% |
| I0 | 2.28% | 1.71% | 1.52% | 0.01% | 0.53% | 1.23% | 2.53% | 9.90% | |
| B3 | Pre-F | 5.18% | 4.93% | 1.59% | 1.40% | 3.90% | 4.86% | 5.79% | 9.98% |
| I0 | 2.75% | 2.31% | 1.50% | 0.00% | 1.20% | 2.14% | 3.09% | 7.40% | |
| B4 | Pre-F | 7.80% | 7.52% | 2.08% | 0.24% | 5.97% | 7.50% | 9.25% | 12.66% |
| I0 | 3.56% | 3.05% | 1.84% | 0.00% | 1.53% | 3.04% | 4.43% | 9.60% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrientos, C.; Mattar, C.; Nakos, T.; Perez, W. Radiometric Cross-Calibration of the Chilean Satellite FASat-C Using RapidEye and EO-1 Hyperion Data and a Simultaneous Nadir Overpass Approach. Remote Sens. 2016, 8, 612. https://doi.org/10.3390/rs8070612
Barrientos C, Mattar C, Nakos T, Perez W. Radiometric Cross-Calibration of the Chilean Satellite FASat-C Using RapidEye and EO-1 Hyperion Data and a Simultaneous Nadir Overpass Approach. Remote Sensing. 2016; 8(7):612. https://doi.org/10.3390/rs8070612
Chicago/Turabian StyleBarrientos, Carolina, Cristian Mattar, Theodoros Nakos, and Waldo Perez. 2016. "Radiometric Cross-Calibration of the Chilean Satellite FASat-C Using RapidEye and EO-1 Hyperion Data and a Simultaneous Nadir Overpass Approach" Remote Sensing 8, no. 7: 612. https://doi.org/10.3390/rs8070612
APA StyleBarrientos, C., Mattar, C., Nakos, T., & Perez, W. (2016). Radiometric Cross-Calibration of the Chilean Satellite FASat-C Using RapidEye and EO-1 Hyperion Data and a Simultaneous Nadir Overpass Approach. Remote Sensing, 8(7), 612. https://doi.org/10.3390/rs8070612