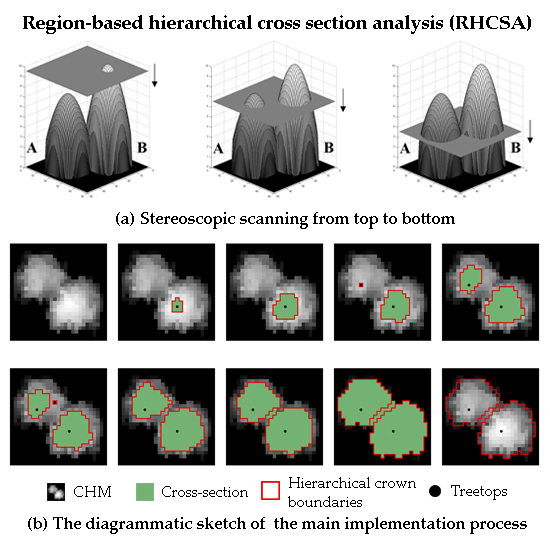
1. Introduction
Forests are an important natural resource which play a significant role in modulating stores and fluxes of water and carbon, maintaining ecological diversity, and regulating climate on the Earth’s surface, and provides timber and other forest products constantly which are closely related to humans [
1,
2,
3]. Parameters of individual trees, such as tree location, tree species, tree height, diameter at breast height (DBH), and crown diameter, are vital for sustainable and precise forest management [
4,
5,
6]. These individual tree-related properties can also be utilized to estimate forest parameters at stand level, such as tree species composition, mean tree height, timber volume, canopy density, and mean basal area [
7,
8,
9,
10].
Traditionally, forest parameters at the individual tree level have been measured by means of field surveys [
11], which are time consuming and cost-intensive when carried out over broad areas [
12,
13]. Since the early 1960s, with the extensive application of remote sensing data in forest inventory [
14,
15,
16] a variety of image processing techniques were developed for automatically detecting and delineating individual tree crowns, such as local maxima filtering with fixed or variable window size [
17,
18,
19], valley-following [
20,
21,
22], region-growing [
23,
24], and watershed segmentation [
25,
26]. These methods make it possible to obtain individual tree-based attributes that can be directly used as input parameters for environmental modeling without the limitations of the sample sizes and inaccessible areas [
27,
28]. In recent decades, airborne Light Detection and Ranging (LiDAR), also referred to airborne laser scanning (ALS), is becoming one of the most common remotely-sensed data sources for forest inventory analysis [
29,
30,
31]. LiDAR remote sensing can provide detailed and precise three-dimensional structural information of the forest area [
32], thus improving the development of individual tree crowns delineation (ITCD) algorithms [
4,
33]. Laser-based individual tree crown delineation can reflect accurate geometrical properties of trees, such as tree height and crown diameter which cannot be affected by illumination angle and shadows on multispectral imageries [
34], and become attractive techniques for both forestry and remote sensing communities [
13].
According to the inputs of ITCD algorithms, LiDAR data can be mainly divided into three categories: LiDAR point cloud, LiDAR-derived raster, e.g., canopy height model (CHM), and raster-point combined data [
13]. With the increased point density of LiDAR data, a growing number of ITCD studies have begun to use LiDAR point clouds directly as the data source. Point cloud-based methods take advantage of multi-return information to describe vertical characteristics under canopies [
35], which cause low information loss and provide an opportunity to multi-layer forests structure modelling [
36,
37]. For example, Ferraz et al. [
38] firstly defined forest layers and then applied a clustering method based on mean-shift algorithm using LiDAR point cloud. Vega et al. [
39] developed a multi-scale dynamic segmentation method called PTrees to extract individual trees from point clouds. However, the method that focused on full exploitation of 3-D points may be currently restricted by computational burden, which is difficult to be applied broadly [
40,
41]. Since raster-based methods are easy to be exploited and improved by powerful knowledge-based approaches [
6,
13], it becomes the most commonly used method for individual tree crown delineation. CHM, a type of LiDAR-derived raster, is the dominant dataset for representing canopy surface in individual tree crown delineation [
8]. Besides CHM, other LiDAR-derived datasets, such as Height-Scaled Crown Openness Index (HSCOI) and Canopy Maximum Model, were also used for ITCD [
42,
43]. Sometimes, researchers combined both raster and LiDAR point data for ITCD studies. For example, researchers applied CHM for the initial segmentation and subsequently refined the results using a LiDAR point cloud [
4,
44,
45].
Recently, many ITCD methods have been developed and applied for various forests conditions [
43,
46,
47]. Thereinto, most studies focus on coniferous forest because (1) many study area were located in high latitude regions that are dominated by coniferous forests; and (2) the basic assumption of a conical crown shape which many algorithms were developed based on is more appropriate for conifers than other forest types [
11]. However, it is not easy to obtain satisfied accuracy under other forest conditions. Ke and Quackenbush [
34] compared watershed segmentation, region-growing, and valley-following method for different forest types on different images and found that all methods works well on coniferous stand and have demonstrated lower accuracy for the deciduous stand on either image set. Other researchers also found that the results of individual tree crown detection are largely influenced by forest types [
48,
49]. Over-segmentation and under-segmentation may be greatly increased in complex and closed forests.
Majority of previous methods extracted individual tree crowns by two steps: (1) treetop detection; and (2) crown boundary delineation. Most treetop detection methods assumed that a treetop is the local maximum brightness or height value and detected individual treetops using local maxima filter. However, during treetop detection, branches, or sub-crowns of a deciduous tree may be detected as small trees (commission error), and small trees with smaller crown size or tree height than average trees tended to be omitted (omission error). To avoid issues mentioned above, researchers have developed a series of local maxima filters with variable window sizes to detect individual treetops [
16,
19,
43]. Although local maximum filtering with variable window sizes has been widely developed and used, structure of tree crowns are not always regular and cannot be represented by a simple 2-D filtering window. In the crown delineation process, watershed segmentation and region-growing, as two of classic image segmentation methods, were often employed based on the markers produced by treetop detection [
16,
43]. Although, researchers have improved delineation algorithms by priori knowledge and morphology of crowns [
46,
50], the two-steps methods could transfer errors from treetop detection to crown boundary delineation procedure.
Researchers also developed some ITCD algorithms without prior treetop detection. For example, Jing et al. [
51] segmented multispectral images at different scales by watershed algorithm and then integrated the multi-layered segments. This approach effectively reduced the over-segmentation which are caused by branches of the deciduous tree, but required the dominant tree crown sizes beforehand. Liu et al. [
52] developed a boundary refining program called Fishing Net Dragging (FiND) based on watershed segmentation and used a boundary classification model to merge the adjacent segments. These approaches do not rely on prior detected treetops, but require some complicated post-process procedures.
Beyond the ITCD algorithms, accuracy assessment for ITCD studies also varies greatly, which make it difficult to compare the performance of the algorithms [
35]. Some studies evaluated ITCD accuracy at both plot and individual tree level (e.g., [
16,
34]), while others only provided accuracy assessment at individual tree level (e.g., [
52]). From two-step perspective, ITCD accuracy assessment can be divided into detection accuracy and delineation accuracy assessment. Pouliot et al. [
53] proposed accuracy index (AI) to represent detection accuracy and used the root mean square error (RMSE) of the crown diameters between reference and delineated crowns for delineation accuracy. Ke et al. [
11] used a confusion table to describe the detail of tree crown detection and evaluated accuracy from both producer’s and user’s perspectives. Some studies used overall accuracy that was evaluated by the number of matched reference and detected trees [
4,
51]. While some researchers analyzed different cases of individual tree crowns matching [
51,
52]. It is necessary to develop a comprehensive and stable accuracy assessment system which contains individual tree crown matching and other accuracy indices for ITCD studies.
In this study, we aimed to propose a novel ITCD algorithm for different forest types in northeastern China based on LiDAR data. The specific objectives were to (1) develop a one-step ITCD algorithm that combines the procedures of treetop detection and crown boundary delineation into an iterative process, which could utilize horizontal relationship among crowns in vertical direction to reduce commission and omission errors; (2) explore the proposed algorithm under different forest types with high canopy density, including coniferous forest, deciduous forest, and conifer-broadleaves forest, and compare it with the marker-controlled watershed algorithm; (3) combine beneficial and complementary aspects of existed accuracy assessment methods into a new ITCD accuracy assessment program to evaluate the accuracy of proposed algorithm. It could provide technical support for individual tree crown delineation in coniferous, deciduous, and mixed forests with high canopy density.
6. Conclusions
Individual tree crown delineation using airborne LiDAR techniques plays a significant role in precise forestry and forest inventory and analysis. In this study, we developed a region-based hierarchical cross-section analysis (RHCSA) for treetop detection and crown delineation using LiDAR-derived CHM. This novel method used level cutting method to detect individual trees and delineate its horizontal boundaries at each level through an iterative process. The proposed algorithm is a one-step individual tree crown delineation (ITCD) algorithm with a few user-defined parameters and not influenced by treetop detection accuracy. Additionally, we also developed a comprehensive accuracy assessment scheme which could provide a guidance for ITCD studies and future applications using single tree approach.
Results showed that RHCSA method obtained stable and high accuracy for different forest types, including coniferous forest, coniferous-broadleaves forest and deciduous forest. The accuracies of mixed forest plots were highest (i.e., producer’s accuracy (PA): 87.02%, user’s accuracy (UA): 85.88%, overall accuracy (OA): 86.44%), followed by coniferous plots (i.e., PA: 85.35%, UA: 84.91%, OA: 85.12%) and deciduous plots (i.e., PA: 85.24%, UA: 82.55%, OA: 83.87%). The detection and delineation accuracy (i.e., RMSE(P) and RMSE(D)) were relatively small (less than 1 m). RHCSA method effectively improved OA by more than 10% comparing with the traditional marker-control watershed segmentation (MCWS) algorithm, especially for deciduous forest (more than 20%) and mixed forest (about 20%). Both RHCSA and MCWS algorithms could provide accurate information on tree location and crown diameter for overall matched trees (less than 1 m for detection accuracy; around 0.5 m for delineation accuracy). However, there are still some limitations in RHCSA method. Since the RHCSA process only considers the segmentation of canopy surface, some intersected crowns and small crowns under the surface are difficult to detect and delineate. Next, RHCSA has been designed and tested for boreal temperate forest. It is still necessary to investigate the performances of other forests (e.g., bamboo forests and rainforests). In addition, although it is suitable to use the RHCSA algorithm for a relatively flat area, the effect of topographic factors (e.g., slope) on accuracy should be explored in the future. In future, ITCD studies could combine basic image segmentation algorithms and tree morphological characteristics to improve the accuracy of the crown delineation based on LiDAR point cloud data.