National BDS Augmentation Service System (NBASS) of China: Progress and Assessment

Abstract

In this contribution, the processing strategies of real-time BeiDou System (BDS) precise orbits, clocks, and ionospheric corrections in the National BDS Augmentation Service System (NBASS) are briefly introduced. The Root Mean Square (RMS) of BDS predicted orbits are better than 10 cm in radial and cross-track components, and the accuracy of the BDS real-time clock is better than 0.5 ns for Inclined Geosynchronous Orbit (IGSO) and Mid Earth Orbit (MEO) satellites. The accuracy of BDS Geostationary Earth Orbit (GEO) orbits and clocks are worse than the IGSO and MEO satellites due to its poor geometry conditions. The real-time ionospheric correction is evaluated by cross-validation, and the average accuracy in the vertical direction is about 4 TECU. With these real-time corrections, the overall single and dual-frequency kinematic precise point positioning (PPP) performance in China are evaluated in terms of positioning accuracy at the 95% confidence level and convergence time. The BDS PPP positioning accuracy shows significant regional characteristics due to the geometry distribution of BDS satellites and the accuracy of ionospheric model in different regions. The BDS dual-frequency PPP positioning accuracy in high-latitude and western fringe region is about 0.5 m and 1.0 m in the horizontal and vertical component, respectively, while the horizontal accuracy is better than 0.2 m and the vertical accuracy is better than 0.3 m in the midlands. The convergence time of the BDS PPP is much longer than the GPS PPP and it needs more than 60 min to achieve the accuracy better than 10 cm in both horizontal and vertical directions for dual-frequency PPP. Similar with dual-frequency PPP, the positioning accuracy of the BDS single-frequency PPP in the fringe region is worse than other regions. The positioning in the midlands can achieve 0.5 m in horizontal component and 1.0 m in the vertical component. In addition, when GPS and BDS are combined, the positioning performance of both single-frequency and dual-frequency PPP can be greatly improved.

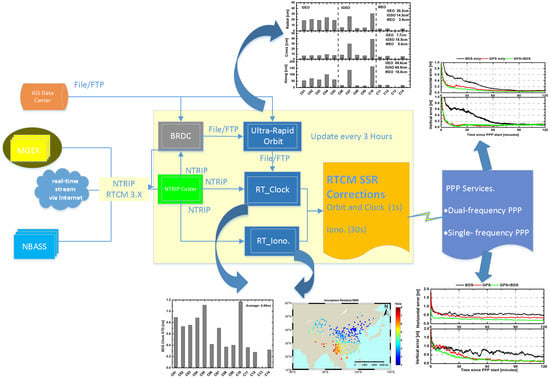
1. Introduction

In order to provide real-time precise positions which are demanded by many time-critical applications, such as geohazard early warning, the International GNSS service (IGS) [1] established a Real-Time Working Group (RTWG) in 2001 with the goal of providing real-time service (RTS). In 2007, IGS started the real-time pilot project (RTPP), supported by the infrastructure of the real-time GNSS data streams from a well-distributed global network. Based on the real-time GNSS observations, real-time precise satellite orbit and clock products are generated and broadcast to users via the Internet by IGS RTPP coordinators. After a six-year experimental test, IGS officially announced the real-time service (RTS) on 1 April 2013, providing GPS and GLONASS real-time orbit and clock corrections which were linked to several centimeters for orbits and sub-nanoseconds for clocks to enable real-time precise point positioning (PPP) for global users [2,3].

PPP enables real-time troposphere [4,5] and space weather monitoring, rapid detection, and the location and characterization of hazardous events, such as earthquakes and tsunamis [6,7,8]. In addition, there are plenty of real-time applications which require sub-meter accuracy using low-cost receivers. Hence, single-frequency PPP is also really interesting for many applications [9,10]. The main challenge of single-frequency PPP is the mitigation of ionospheric delays. Although the GRAPHIC (GRoup And PHase Ionospheric Correction) [11] method can be used to reduce the ionosphere impacts by combining pseudorange and carrier-phase measurements, Muellerschoen et al. pointed out that GRAPHIC-based single-frequency PPP asked for a period of about 20 min for converge [12]. Analyzing the spatio-temporal characteristics of ionospheric delays, Shi et al. developed a new single-frequency PPP model, the convergence and the accuracy of single-frequency PPP with this method will be better if more precise ionospheric product is provided [10].

In order to reduce the positioning error caused by ionospheric delay, GNSS systems, such as GPS, BDS, and Galileo, provide ionospheric models via satellite broadcast messages, i.e., the Klobuchar and the NeQuick model [13,14,15]. However, these empirical models, including the GPS/BDS Klobuchar model and NeQuick model, can only compensate 60–70% of the propagation error induced from ionospheric delay. In addition to these empirical models, like Klobuchar or NeQuick, there have been several real-time ionospheric products which can be used for single-frequency PPP. SBAS (satellite-based augmentation system) can broadcast ionospheric corrections to users through geostationary satellites. The corrections consist of vertical total electron content (VTEC) values on a single-layer grid at a height of 350 km. The spatial resolution of the ionosphere grid points (IGPs) is spaced by 5° in both latitude and longitude, increasing to 30° in longitude between 85° and the poles, which is updated every 5 min. The IGS Ionosphere Working Group routinely provides global ionosphere maps (GIMs) of VTEC. The IGS GIMs are provided with a temporal resolution of 1 h and a spatial resolution of 5.0 degrees and 2.5 degrees, respectively, in longitude and latitude. There are three types of IGS GIMs: the final, rapid, and predicted products. The GIMs used for real-time applications are predicted to the next one or two days [16]. Different from the SBAS ionospheric models and GIMs, the research group of Astronomy and GEomatics (gAGE) has developed an ionospheric model with two layers at heights of 270 and 1600 km [17] and a real-time estimation of the IGPs is made every 5 min in regions where GNSS observations are available. By processing GPS observations from 60 IGS and EUREF reference stations, Abdelazeem et al. develop a real-time regional ionospheric model (RT-RIM) over Europe, it was proved that the PPP performance by the RT-RIM in mid-latitude can be improved about 40% in comparison with the IGS GIM [18].

With the rapid development of GNSS, several global or regional satellite navigation systems are deployed to provide pilot services, e.g., BeiDou System (BDS), European Galileo, or Japan QZSS. To prepare for incorporation of the new and modernized systems, IGS started the Multi-GNSS Experiment (MGEX) in 2012. By using these real-time streams, Centre National d’Études Spatiales (CNES) provides publicly available real-time corrections for all the GNSS, including BDS. However, the BDS tracking stations in the MGEX network are not uniformly distributed, most of those are in Europe and can only track BDS MEO satellites. Only a few BDS real-time stations are located in Asian-Pacific regions. Kazmierski et al. evaluated the availability and the accuracy of CNES real-time corrections and found that the availability of real-time corrections in their test period was at the level of about 80% for BDS and about 90% for the remaining GNSS systems [19]. Obviously, at present, the CNES real-time GNSS service cannot supply reliable corrections for BDS. On the other hand, the studies about BDS real-time PPP applications are almost based on simulated real-time mode and only a small amount of stations in China are used for BDS dual-frequency and single-frequency PPP performance evaluation [20,21].

In order to promote the development of the BDS real-time precise applications, the project of National BDS Augmentation Service System (NBASS) is planned to establish from 2014. There have been 150 uniformly nationwide real-time reference stations in China. In addition, NBASS is powered by the real-time PANDA (Positioning and Navigation Data Analyst) software developed by Wuhan University [22], which can satisfy the BDS real-time PPP service. As the RTCM-SSR still does not support the BDS constellation and the representation of the ionospheric corrections, the SSR messages for BDS orbit and clock corrections are designed to maintain the standards and formats with IGS, as well as the ionospheric corrections.

In this contribution, the tracking network of NBASS will be first briefly introduced in Section 2, as well as the generations of the real-time orbit, clock, and ionospheric corrections. Furthermore the accuracy of the BDS real-time orbit, clock, and ionospheric corrections will be evaluated in Section 3. With the real-time corrections, the subsequent section shows the overall performance of BDS dual-frequency and single-frequency PPP in China, including the positioning accuracy and the convergence performance. By the end, some discussions and conclusions will be given in Section 5 and Section 6, respectively.

2. NBASS Tracking Network and Processing Strategy

In order to improve the performance of BDS real-time positioning and promote the application of BDS, NBASS was launched by China North Industries Group Corporation on 11 September 2014. NBASS aimed to provide BDS all kinds of precise positioning services for different applications. Some details about the tracking network and the processing strategy of NBASS will be shown in the following sections.

2.1. NBASS Tracking Network

There have been more than 150 stations which can provide real-time multi-GNSS observation streams across China. Figure 1 shows the distribution of the reference stations, all these stations are equipped with GNSS receivers including PDB38, UR380, VNet8, and N72 manufactured by Shanghai ComNav Technology Ltd. (Shanghai, China), the UNICORE Company (Beijing, China), Guangzhou Hi-Target Navigation Tech. Co., Ltd. (Guangzhou, China), and Shanghai China Navigation Technology Co., Ltd. (Shanghai, China), respectively. All these receivers can track eight frequencies of GNSS signals of three satellite navigation systems, including BDS B1, B2, and B3, GPS L1, L2, and L5, and GLONASS L1 and L2.

2.2. Processing Strategy

The real-time satellite orbit and clock products are crucial to PPP users and the ionospheric product is essential to single-frequency users. In NBASS system, all these real-time products are estimated with GNSS observations from the NBASS tracking network and MGEX. PANDA software is modified to generate the real-time BDS orbits, clocks, and ionospheric corrections. The processing strategies are introduced as following. With these real-time products, a real-time PPP engine is also presented in the final part of this section.

2.2.1. Orbit and Clock Products

In order to obtain the BDS orbits with higher accuracy, we should take full advantages of the available real-time BDS streams from NBASS and MGEX, and the solutions should be estimated with the combination of BDS and GPS observations. In real-time applications, the update rate of the BDS predicted orbits is usually 3 h in order to guarantee favorable accuracy. In an attempt to balance the BDS/GPS orbits accuracy and the processing efficiency, we obtain the predicted BDS orbits from a 3-day POD (precise orbit determination) solutions. BDS precise orbits are estimated with 72 h of observations from MGEX + NBASS network. The distribution of the stations used in the POD is shown in Figure 2, in which the red circles and green circles are stations from MGEX and NBASS network for BDS three-day POD. The hourly data from MGEX stations are downloaded by FTP [23] and the real-time data streams from NBASS network are recorded in hourly files. In the processing of BDS/GPS POD, the B1/B2 and L1/L2 ionosphere-free combinations are used. The reduced CODE solar radiation pressure (SRP) model with five parameters [24] is employed for all BDS and GPS satellites. For all the BDS satellites, the antenna phase center offsets recommended by MGEX (${\mathrm{x}}_0=0.60\mathrm{m}$, ${\mathrm{y}}_0=0$ m, ${\mathrm{z}}_0=1.10\mathrm{m}$) is adopted while the phase center variations are not corrected. For more details about the dynamical orbit models and processing strategies about BDS/GPS POD, we refer to [25,26].

Real-time satellite clock corrections are usually estimated by the undifferenced, the epoch-differenced, or the mixed-differenced mode. It is proved that the mixed-differenced method can reduce the computation time significantly compared with undifferenced method and achieve better accuracy than the epoch-differenced method in [27]. With mixed-differenced method, it is shown to be efficient enough to produce 1-Hz BDS/GPS clocks for real-time applications in a simulated real-time mode [28]. Due to these advantages, the mixed-differenced method is adopted to estimate the BDS/GPS real-time clock with about 75 stations and the distribution of stations from the MGEX and the NBASS tracking network for clock estimation is shown in Figure 2. For more details about the estimation of real-time satellite clock, we refer to [28].

2.2.2. Ionopshere Products

The ionospheric STEC (slant total electron content) can often be calculated by using phase-smoothed pseudorange observations and the VTEC is modeled in a solar-geomagnetic reference frame by using spherical harmonic models. As only real-time ionosphere delays are modeled in China, a low-order spherical harmonic model is used, which is well-suited for regional areas [29]. Zhang et al. chose a spherical harmonic function of degree and order 4 for modeling regional ionospheric delays with BDS and GPS observations across China [30]. In the real-time ionospheric modeling, we choose a spherical harmonic function of degree and order 5 with the BDS and GPS observations collected at all the stations shown in Figure 1. On the other hand, as the satellite Differential Code Biases (DCB) are stable over a long period, DCBs from IGS and MGEX are fixed and only 36 spherical harmonic parameters and the receiver DCBs are estimated in a real-time mode. The update rate of the real-time products is 30 s.

2.2.3. Real-Time PPP

All real-time corrections are encoded in RTCM-SSR format and sent to users via Internet. By retrieving and decoding the real-time messages, the real-time PPP engine can be operated in different ways, including dual-frequency or single-frequency PPP with BDS/GPS observations. The processing strategy for real-time single- and dual-frequency PPP is depicted in Figure 3 including BDS and GPS PPP. Based on the generated PPP model with raw observations in [21], the PANDA software is modified for real-time single- and dual-frequency PPP. The ionosphere-free observation is used in dual-frequency PPP, while the single-frequency PPP is based on the raw observations and the real-time ionospheric corrections are used in PPP as a priori constraint. In order to obtain high accuracy positioning, PPP users should adopt the same model with the models in clock estimation. We use the same observation models in real-time clock estimation shown in

Table 1. Observation models involved in BDS/GPS POD and clock estimation.

Item	POD	Clock Estimation
Estimator	Least squares	Square root information filter
Processing sampling	300 s	1 s
Ambiguity	Fixed for GPS/BDS(IGSO, MEO) separately	Epoch-differenced method
Earth rotation parameters	Estimated with tight constraint	Fixed
Coordinates	Estimated with tight constraint	Fixed
Observables	Un-differenced ionosphere-free combination of code and phase based on GPS L1/L2, BDS B1/B2
Weighting	Elevation dependent weight ($p=1,e>{30}^{°};p={\sin }^{2}e,e\le {30}^{°}$ (p is the observation weight and e is satellite elevation angle)
Cutoff elevation	7°
Satellite phase center	igs08.atx
Receiver phase center	igs08.atx for GPS, none for BDS
Phase wind-up	Corrected [31]
BDS pseudo-range bias	Corrected [32]
Tropospheric delay	Initial model (Saastamoinen [33] and GPT2 [34]) + random-walk process 10 cm, 5 mm/√(h)
Satellite clock	Estimated as white noise
Receiver clock	Estimated as white noise
Inter-system biases	Estimated as constant parameters with zero mean condition

, except for the observation weighting for BDS GEO. In our real-time PPP processing, the weight of BDS GEOs is one third that of other satellites. For more information about the PPP model, we refer to [10,21].

3. Accuracy Evaluation of Real-Time Orbit: Clock and Ionospheric Corrections

One week of real-time corrections from 22 January 2016 to 28 January 2016 are used for accuracy evaluation. We first assess the accuracy of the predicted BDS orbit products compared with the MGEX final products. As there is still no combination product of BDS orbits in IGS, the BDS predicted orbit is also evaluated by the overlap comparison with the solution of POD. Then, the BDS real-time satellite clocks are compared with the MGEX final clock products. Finally, a cross-validation is done to evaluate the real-time ionospheric modeling with about 230 stations from CMONOC (Crustal Movement Observation Network of China).

3.1. BDS Orbit Results

In order to evaluate the quality of BDS orbits, the overlap comparison and the difference with GBM orbit from MGEX are performed. Figure 4 shows an illustration of the overlap comparison of the 3-h predicted orbits and the post-processing solution. The accuracy of MEO satellites is the best among the three type of satellites, achieving sub-decimeter level, especially the accuracy in the radial and the cross-track components. For GEOs, the average RMS of the along-track is 69.6 cm and the accuracy in radial and the cross-track is better than the along-track. It is noted that the accuracy of C07 and C10 is worse than other IGSOs in each direction, which is caused by the inaccurate SRP and the switch model for the yaw-attitude and the normal-attitude in eclipsing seasons. It is pointed out that the inaccurate attitudes can seriously impact on the accuracy of the POD solutions and cause difficulty on the SRP modeling which can also result in significant orbit errors [14]. Other than C07 and C10, other IGSO orbit products have the same accuracy level as BDS MEOs. The average RMS values of the differences between the predicted orbits and the GFZ solutions for each satellite are presented in Figure 5. It is shown that the results in Figure 5 are similar to that in Figure 4, the orbit differences of GEOs, C07, and C10 is larger than other IGSOs and MEOs and the RMS are about 5.4 cm, 8.7 cm, and 22.3 cm in radial, cross-track, and along-track, respectively. By the analysis of overlap comparisons and the differences from GFZ orbits, it shows that the BDS IGSO and MEO 3-h predicted orbits can achieve decimeter level accuracy and the further study about the attitude model, the SRP model during eclipsing seasons is necessary. The accuracy of predicted GEO orbits is about several meters and worse than those of the IGSOs and MEOs. The reason of the poor orbit accuracy for GEO satellites is mainly due to the poor satellite geometry. These poor geometry conditions weaken the observability of the orbit dynamics, affecting the estimated orbit parameters. Hence, the weight of GEO in real-time PPP should be smaller than other satellites [19].

3.2. Real-Time BDS Clock Results

In an attempt to assess the real-time BDS clock product, the differences between the real-time clock product and the GFZ clock product are calculated. The derived time series are aligned to a reference satellite in order to remove the system bias, which follows the standard IGS clock comparison procedure [15]. Then the STD values which represent the real-time clock precision are calculated over the seven-day period.

Figure 6 shows the average clock accuracy for each BDS satellite. The average STD values for BDS clock is 0.65 ns. It is noted that the STD values of BDS GEO clock as well as IGSO C07 and C10 are larger than the other IGSOs and MEOs, which are caused by their worse orbit accuracy. As mentioned in Section 3.1, the IGSO C07 and C10 were in eclipsing seasons, both the orbit and the clock accuracy are poor during this period, it means that the eclipsing seasons have a negative effect on both orbits and clock. Fortunately, once the BDS yaw attitude model and the solar radiation pressure model in eclipsing seasons are improved, the accuracy of BDS orbits and clocks will get better. Other than the C07 and C10, the accuracy of BDS IGSOs and MEOs clock is about 0.3 ns. It is well-known that the radial orbit errors can be partly compensated by the clock estimation and, thus, real-time PPP may not be seriously affected by poor orbit accuracy. Hence, the PPP performance is also a way to evaluate the clock accuracy and it will be analyzed in the Section 4.

3.3. Ionospheric Correction

The cross-validation is adopted to evaluate the real-time ionosphere corrections. The referenced ionosphere delay is extracted from evenly distributed stations with post-processing PPP. The ionosphere residual at each station is calculated by the following equation:

$$\mathsf{\Delta }{\mathrm{ion}}_{i,k}^j= {{\mathit{VTEC}}_{\mathit{model}}}_{i,k}^j-{\mathit{VTEC}}_{i,k}^j$$

(1)

where $VTE{C}_{{model}_i^j}$ is the VTEC at interpolated from the real-time ionosphere map at the IPP (ionosphere pierce point) from station i to satellite j, $VTE{C}_i^j$ is the referenced VTEC calculated by the measurements at the rover stations, k represents the epoch and the interval is 30 s. The difference between the modeled ionosphere delay and the referenced value is the ionosphere residual $\mathsf{\Delta }{\mathrm{ion}}_{i,k}^j$ for each station-satellite pair. The accuracy of real-time ionosphere products is evaluated by the RMS of the ionosphere residual using Equation (2) at each station:

$$RM{S}_{ion,i}=\sqrt{\frac{{{\displaystyle \sum }}_{k=1}^{nEpo}{{\displaystyle \sum }}_{j=1}^{nSat}{\left(\mathsf{\Delta }{\mathrm{ion}}_{i,k}^j\right)}^2}{n}}$$

(2)

where nEpo, nSat, and n is the epoch number, satellite number and the sample number at the station i, respectively.

We select about 230 stations from CMONOC network with good distribution in China, which is maintained by China’s earthquake administration. Figure 7 plots the ionosphere residual RMS variations at each station in DOY 22, 2016. The ionosphere residual RMS shows significant regional differences. The accuracy of ionosphere corrections in high latitudinal regions is better than 3 TECU, and is better than that in the low-latitude region. The reason is mainly the active ionosphere in the low-latitude and the sparse distribution of tracking stations in western region as shown in Figure 1. It is shown that the accuracy of real-time ionospheric model is 1–8 TECU in Figure 7, which is compatible with IGS final products. Figure 8 shows the average RMS of each station in every day and the average RMS of the week is about 4 TECU.

4. Real-Time Kinematic PPP Results

We conduct two experiments to analyze the performance of real-time kinematic BDS and GPS PPP. In the first experiment, in order to evaluate the overall performance of real-time PPP in China, a number of evenly-distributed stations in China are selected to simulate dual-frequency and single-frequency PPP. In the second experiment, we will show the results of shipboard kinematic PPP.

4.1. Simulated Kinematic Real-Time PPP

In this section, the positioning accuracy and convergence of both single and dual-frequency simulated kinematic PPP are analyzed using 30 evenly-distributed stations in China. It should be noted that, these evaluated stations are not used to calculate orbit and clock products. One week of results (DOY022–027, 2016) at these stations were collected and the real-time PPP positioning error at the 95% confidence level is calculated to evaluate the positioning accuracy. The coordinates of these stations are calculated in post-processing mode using PANDA every day. We obtain the high-accuracy coordinates from the average of the weekly calculation. For PPP convergence time, the PPP engine is restarted at UTC 0:00 in DOY073 and all the results from stations shown in Figure 1 are carried out by statistics to evaluate the mean convergence time.

4.1.1. Real-Time Dual-Frequency PPP

Figure 9 shows the horizontal and vertical accuracy of BDS dual-frequency PPP at the 95% confidence level, respectively. It can be seen that the BDS dual-frequency PPP shows significant regional difference: the accuracy in Northeast and Northwest China is worse than in other areas. As BDS is still a regional navigation system, it can only provide service in the Asian-Pacific region, the geometric dilution of BDS satellites is poorer in northeast and northwest areas than other areas, which results in worse solution. BDS-only dual-frequency PPP can achieve the accuracy of 0.2 m in horizontal and 0.3 m in vertical in middle and low latitude regions, while the horizontal and vertical accuracy is about 0.5 m and 1 m in north-east and north-west regions, respectively. Different from BDS-only PPP, the GPS-only PPP positioning accuracy (as shown in Figure 10) has no regional discrepancy in China, and can achieve an accuracy uniformly better than 0.2 m in the horizontal and 0.3 m in the vertical, respectively. It can be also seen that the horizontal accuracy of BDS-only dual-frequency PPP in low and middle-latitude is compatible with GPS PPP while the vertical accuracy is slightly worse.

Figure 11 illustrates the mean convergence times of BDS-only, GPS-only, and BDS/GPS dual-frequency PPP at all stations as shown in Figure 1. Compared to GPS PPP, the convergence time of BDS-only PPP is longer and it needs more than 60 min to obtain the accuracy better than 0.1 m. The convergence of GPS-only PPP needs about 45 min to achieve the accuracy better than 0.1 m in horizontal, which is consistent with IGS real-time PPP. When combining the BDS and GPS, the convergence time is significantly reduced and the horizontal accuracy better than 0.1 m can be achieved within 30 min. However, the convergence of BDS/GPS dual-frequency PPP has no significant improvement in the vertical direction.

4.1.2. Real-Time Single-Frequency PPP

Like the above analysis of dual-frequency, the positioning accuracy at the 95% confidence level in both horizontal and vertical directions of BDS-only and GPS-only single-frequency PPP are represented in Figure 12 and Figure 13. Similar to the BDS-only dual-frequency PPP, the BDS single-frequency PPP achieves worse positioning accuracy in northeast and northwest regions than other regions in China. On the other hand, the performance of single-frequency PPP is affected by the ionosphere which is more active in low-latitude. The positioning accuracy of GPS single-frequency PPP is a little worse in low latitude region, especially in vertical direction. For GPS-only single-frequency PPP, the horizontal accuracy is about 0.5 m and the positioning accuracy in vertical direction is from 0.5 to 1 m. On the contrary, for BDS-only single-frequency PPP, the positioning accuracy at the 95% level is about 2 m in horizontal and 3 m in vertical in the northeast and northwest regions, while the accuracy in low-latitude regions is better than that in these regions, the horizontal accuracy is about 0.5 m and 1 m in the vertical direction. It seems that single-frequency PPP is more sensitive to the satellite geometry than the effect of ionosphere.

Figure 14 represents the average positioning error as a function of time since PPP starts in DOY 73, for all the stations as shown in Figure 1. It reflects the convergence time of BDS-only, GPS-only, and BDS/GPS single-frequency PPP. It is interesting that the BDS/GPS single-frequency PPP greatly reduces the convergence time of BDS-only and GPS-only single-frequency PPP. On the other hand, the combination of BDS and GPS can greatly improve the positioning accuracy in horizontal direction and the average positioning accuracy is about 0.25 m. It should be noted that the sub-meter positioning accuracy can be achieved within 5 min for BDS-only, GPS-only single-frequency PPP. With the combination of BDS and GPS, the multi-GNSS single-frequency PPP can perform more reliably and with higher accuracy than each individual system.

4.2. Shipboard Real-Time Dual-Frequency PPP

On 30 May 2016, GNSS data were collected at 1 s intervals for a shipboard test in the East Lake of Wuhan, China (Figure 15). Two GNSS receivers with survey antennas (HX-CSX601A) were used in this experiment; one was for the BDS PPP test and the other was for the GPS and BDS combined PPP test. We compare the positioning results of BDS and GPS + BDS PPP with RTK results, which is post-processed. Figure 16 plots the positioning error time series of BDS and GPS + BDS PPP. Obviously, the GPS + BDS PPP outperforms the BDS PPP in terms of positioning accuracy and convergence time. The RMS of BDS PPP is 0.13 m, 0.11 m, and 0.38 m in the east, north, and up direction, respectively. Comparing with BDS PPP, the positioning accuracy of GPS + BDS PPP improves 69.2%, 72.7%, and 42.1% in the east, north, and up direction, respectively. BDS PPP needs more than 2 h to obtain the positioning better than 10 cm in horizontal component, while GPS + BDS PPP need no more than 5 min. For BDS only PPP, the B2 signals of several BDS satellites are locked and the carrier-phase measurements are missing between 04:49:50 and 04:51:12. It is seen that the BDS PPP re-initializes at 04:49:50 in Figure 16. For GPS + BDS PPP, the PPP solution is not affected by the BDS satellites data loss between these epochs, and the positioning accuracy is at the centimeter level.

5. Discussion

By the analysis of the initial results of BDS real-time orbits, clocks, ionospheric modeling and PPP, several future works should be overcome in the NBASS. Due to the imprecise models of BDS satellite attitude and the SRP in the eclipsing seasons, the accuracy of predicted orbits and real-time clocks is poor which may affect the real-time positioning performance. In addition, the PPP convergence time is still too long, especially the BDS PPP. It is demonstrated that the PPP can achieve better accuracy and reduce the convergence time with ambiguity-fixing methods, PPP-RTK based on the NBASS network will be studied and we expect to reduce the convergence time of BDS/GPS PPP and achieve a more reliable solution. At the same time, it should also be noted that the more constellations that are integrated, the better and more reliable solutions can be achieved. In order to exploit the benefits of multi-GNSS signals tracked by the NBASS network, GLONASS will be combined with BDS and GPS. The estimation of real-time GLONASS orbits and clocks is in the testing phase and will be provided in the next phase.

6. Conclusions

In this contribution, the National BDS Augmentation Service System, and its performance, are briefly introduced. The real-time BDS orbit, clock, and ionospheric corrections are estimated with the observations from the NBASS and MGEX networks. It is shown that the performance of overall BDS real-time orbits and clocks is worse than GPS, because of the reduced constellation and the non-uniformly distributed tracking stations for BDS. The BDS GEOs are relatively stationary to the tracking stations and the poor geometry weakens the observability of the orbit dynamics. On the other hand, due to the imprecise models of the satellites’ attitude, SRP, etc., the accuracy of predicted BDS IGSO and MEO orbits is negatively affected during eclipsing seasons. The estimate of satellite clock offset strongly correlates with radial orbit error and, hence, the clock accuracy is also affected for the satellites in the eclipsing seasons. Fortunately, the accuracy of BDS IGSO and MEO orbits are at the decimeter level when they are not eclipsing, and it is better than 10 cm in the radial and cross-track components, respectively. For BDS IGSO and MEO real-time satellite clock products, the accuracy is better than 0.5 ns compared with the GFZ products. By a cross-validation of the real-time ionospheric corrections, the accuracy of the VTEC is better than 8 TECU and shows obvious region-specific features. The ionosphere accuracy is better than 3 TECU in the high latitude regions and the average accuracy in China is about 4 TECU.

With the real-time corrections, the real-time single- and dual-frequency PPP are carried out at the stations from the NBASS tracking network. Both positioning accuracy and convergence performance are evaluated. At present, BDS is still a regional satellite navigation system, so the satellite geometry distribution is not good in the northeast and northwest areas of China; BDS PPP positioning accuracy shows obvious regional characteristics while the positioning accuracy of GPS dual-frequency PPP is at the same level. In low latitude regions, the BDS dual-frequency PPP can achieve the same accuracy as GPS, the horizontal and vertical accuracy can achieve 0.2 m and 0.3 m at the 95% confidence level, respectively. The accuracy of ionospheric corrections is a key factor to single-frequency PPP and the positioning accuracy in low-latitude regions is relatively worse than I high-latitude regions, which is caused by the lower accuracy of the ionosphere in the low latitude regions. Compared with GPS dual-frequency PPP, the convergence time of BDS PPP is much longer and it needs more than one hour to achieve a positioning accuracy better than 10 cm in both horizontal and vertical directions. It is also noted that the convergence time can be shortened and the positioning accuracy can be greatly improved when BDS and GPS are combined.