On the Performance Evaluation of Commercial SAW Resonators by Means of a Direct and Reliable Equivalent-Circuit Extraction
Abstract
:1. Introduction
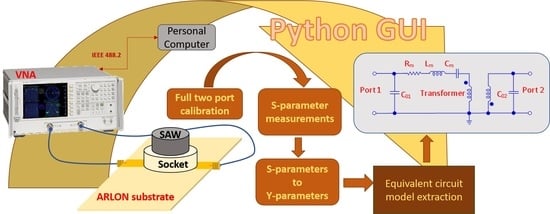
2. Characterization and Theoretical Analysis
2.1. Lorentzian Fitting
2.2. Equivalent Circuit Extraction
3. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rayleigh, L. On waves propagated along the plane surface of an elastic solid. Proc. Lond. Math. Soc. 1885, s1–17, 4–11. [Google Scholar] [CrossRef]
- Hu, M.; Duan, F.L. Design, fabrication and characterization of SAW devices on LiNbO3 bulk and ZnO thin film substrates. Solid State Electron. 2018, 150, 28–34. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, Y.; Carka, D.; Li, F. Surface acoustic wave sensors for temperature and strain measurements. In Proceedings of the IEEE International Ultrasonics Symposium (IUS), Las Vegas, NV, USA, 7–11 September 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Li, B.; Yassine, O.; Kosel, J. A surface acoustic wave passive and wireless sensor for magnetic fields, temperature, and humidity. IEEE Sens. J. 2015, 15, 453–462. [Google Scholar] [CrossRef]
- Gugliandolo, G.; Aloisio, D.; Leonardi, S.G.; Campobello, G.; Donato, N. Resonant devices and gas sensing: From low frequencies to microwave range. In Proceedings of the International Conference on Advanced Technologies, Systems and Services in Telecommunications (TELSIKS), Nis, Serbia, 23–25 October 2019; pp. 21–28. [Google Scholar] [CrossRef]
- Maurya, P.; Mandal, N.; Roy, J.K.; Mukhopadhyay, S.C. A novel approach for wireless liquid level measurement using SAW sensor. In Proceedings of the International Conference on Sensing Technology (ICST), Limerick, Ireland, 4–6 December 2018; pp. 127–131. [Google Scholar] [CrossRef]
- Psychogiou, D.; Gómez-García, R.; Peroulis, D. SAW-based bandpass filters with flat in-band group delay and enhanced fractional bandwidth. In Proceedings of the the IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Pavia, Italy, 20–22 September 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Roy, A.; Nemade, H.B.; Bhattacharjee, R.; Kushwah, V. DQPSK modulation and demodulation using SAW device. IET Commun. 2017, 11, 2630–2636. [Google Scholar] [CrossRef]
- Arthur, J.W. Modern SAW-based pulse compression systems for radar applications. I. SAW matched filters. Electron. Commun. Eng. J. 1995, 7, 236–246. [Google Scholar] [CrossRef]
- Arthur, J.W. Modern SAW-based pulse compression systems for radar applications. 2. Practical systems. Electron. Commun. Eng. J. 1996, 8, 57–78. [Google Scholar] [CrossRef]
- Zenzinger, A.; Zhang, Z.; Seifert, F.; Weigel, R. Application of SAW matched filters for time code division multiple access (TCDMA) systems. In Proceedings of the ISSSTA’95 International Symposium on Spread Spectrum Techniques and Applications, Mainz, Germany, 25 September 1996; Volume 2, pp. 720–724. [Google Scholar] [CrossRef]
- Mukhtar, N.J.; Aziz, N.A.; Bais, B.; Majlis, B.Y. Circuit modeling of surface acoustic wave (SAW) resonator with circular geometry. In Proceedings of the IEEE International Conference on Semiconductor Electronics (ICSE), Kuala Lumpur, Malaysia, 17–19 August 2016; pp. 57–60. [Google Scholar] [CrossRef]
- Wada, T.; Ogami, T.; Horita, A.; Obiya, H.; Koshino, M.; Kawashima, M.; Nakajima, N. A new tunable SAW filter circuit for reconfigurable RF. In Proceedings of the IEEE MTT-S International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Kalinin, V. Wireless physical SAW sensors for automotive applications. In Proceedings of the IEEE International Ultrasonics Symposium, Orlando, FL, USA, 18–21 October 2011; pp. 212–221. [Google Scholar] [CrossRef]
- Yeo, L.Y.; Friend, J.R. Ultrafast microfluidics using surface acoustic waves. Biomicrofluidics 2009, 3, 012002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luong, T.-D.; Nguyen, N.-T. Surface acoustic wave driven microfluidics—A review. Micro. Nanosyst. 2010, 2, 217–225. [Google Scholar] [CrossRef]
- Destgeer, G.; Sung, H.J. Recent advances in microfluidic actuation and micro-object manipulation via surface acoustic waves. Lab. Chip. 2015, 15, 2722–2738. [Google Scholar] [CrossRef] [PubMed]
- Malocha, D.C.; Humphries, J.; Figueroa, J.A.; Lamothe, M.; Weeks, A. 915 MHz SAW wireless passive sensor system performance. In Proceedings of the IEEE International Ultrasonics Symposium (IUS), Tours, Farnce, 18–21 September 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Campobello, G.; Segreto, A.; Donato, N. A new frequency estimation algorithm for IIoT applications and low-cost instrumentation. In Proceedings of the 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Dubrovnik, Croatia, 25–28 May 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Campobello, G.; Segreto, A.; Donato, N. A novel low-complexity frequency estimation algorithm for industrial internet-of-things applications. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Zenomar, B.; Campobello, G.; Longo, F.; Merlino, G.; Puliafito, A. A new fog-enabled wireless sensor network architecture for industrial internet of things applications. In Proceedings of the 24th IMEKO TC4 International Symposium and 22nd International Workshop on ADC and DAC Modelling and Testing, Palermo, Italy, 14–16 September 2020; pp. 179–184. [Google Scholar]
- SAW R2630 datasheet. 418.05 MHz SAW Resonator; Siemens Matsushita Components: Munich, Germany, 1999. [Google Scholar]
- SAR series datasheet. Saw Resonators Specifications: Features and Applications; Murata Electronics North America, Inc.: Smyrna, GA, USA, 1999; pp. 53–54. [Google Scholar]
- SAW RP1308 datasheet. 433.92 MHz SAW Resonator; Murata Electronics N.A., Inc.: Smyrna, GA, USA, 2015. [Google Scholar]
- SAW RP1094 datasheet. 915.0 MHz SAW Resonator; RF Monolithics, Inc.: Dallas, TX, USA, 1999. [Google Scholar]
- Donato, N.; Aloisio, D. Development of a SOLT calibration setup for SAW sensor characterization. Lect. Notes Electr. Eng. 2012, 109, 265–269. [Google Scholar] [CrossRef]
- Gugliandolo, G.; Aloisio, D.; Campobello, G.; Crupi, G.; Donato, N. Development and metrological evaluation of a microstrip resonator for gas sensing applications. In Proceedings of the IMEKO TC-4 International Symposium, Palermo, Italy, 14–16 September 2020; pp. 1–4. [Google Scholar]
- Pompeo, N.; Torokhtii, K.; Leccese, F.; Scorza, A.; Sciuto, S.; Silva, E. Fitting strategy of resonance curves from microwave resonators with non-idealities. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Mehl, J.B. Analysis of resonance standing-wave measurements. J. Acoust. Soc. Am. 1978, 64, 1523–1525. [Google Scholar] [CrossRef]
- Campobello, G.; Crupi, G.; Donato, N. Cryogenic electrical characterization and equivalent-circuit modeling of SAW resonators. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Dubrovnik, Croatia, 25–28 May 2020; p. 5. [Google Scholar] [CrossRef]
- Hashimoto, K. Surface Acoustic Wave Devices in Telecommunications: Modeling and Simulation; Springer: Berlin, Germany, 2000. [Google Scholar]
- Kshetrimayum, R.; Yadava, R.D.S.; Tandon, R.P. Modeling electrical response of polymer-coated SAW resonators by equivalent circuit representation. Ultrasonics 2011, 51, 547–553. [Google Scholar] [CrossRef] [PubMed]
- Kushibiki, J.; Takanaga, I.; Nishiyama, S. Accurate measurements of the acoustical physical constants of synthetic α-quartz for SAW devices. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 125–135. [Google Scholar] [CrossRef] [PubMed]
- Zhgoon, S.; Shvetsov, A.; Ancev, I.; Bogoslovsky, S.; Sapozhnikov, G.; Trokhimets, K.; Derkach, M. SAW temperature sensor on quartz. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 1066–1075. [Google Scholar] [CrossRef] [PubMed]
- Naumenko, N.F. Optimization of LiNbO3/quartz substrate for high-frequency wideband SAW devices using longitudinal leaky waves. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 1485–1491. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Zhang, S.; Zhang, H.; Lv, W.; Zhang, C.; Lv, X.; San, H. Fabrications of L-band LiNbO3-based SAW resonators for aerospace applications. Micromachines 2019, 10, 349. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, C.; Chen, Y.; Cho, C. A three-dimensional finite element analysis model for SH-SAW torque sensors. Sensors 2019, 19, 4290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Z.; Zhang, Q.; Li, C.; Fu, S.; Qiu, X.; Wang, X.; Wu, H. Geometric nonlinear model for prediction of frequency-temperature behavior of SAW devices for nanosensor applications. Sensors 2020, 20, 4237. [Google Scholar] [CrossRef] [PubMed]
- Ondo, J.C.A.; Blampain, E.J.J.; Mbourou, G.N.; Murtry, S.M.; Hage-Ali, S.; Elmazria, O. FEM modeling of the temperature influence on the performance of SAW sensors operating at gigahertz frequency range and at high temperature up to 500 °C. Sensors 2020, 20, 4166. [Google Scholar] [CrossRef] [PubMed]











| SAW Device (Nominal Frequency) | fr (MHz) | Qr | frQr (MHz) | C01 (pF) | C02 (pF) | Rm (Ω) | Lm (μH) | Cm (fF) |
|---|---|---|---|---|---|---|---|---|
| R2630 (418.05 MHz) | 418.03 | 12,514 | 5,231,227 | 2.07 | 1.92 | 117.9 | 561.8 | 0.26 |
| SAR423.22 MDA (423.22 MHz) | 423.25 | 13,649 | 5,776,939 | 1.42 | 1.23 | 105.8 | 542.9 | 0.26 |
| RP1308 (433.92 MHz) | 433.90 | 13,439 | 5,831,182 | 1.94 | 1.41 | 80.3 | 395.8 | 0.34 |
| RP1094 (915 MHz) | 914.80 | 7988 | 7,307,422 | 2.88 | 2.97 | 47.5 | 66.0 | 0.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gugliandolo, G.; Marinković, Z.; Campobello, G.; Crupi, G.; Donato, N. On the Performance Evaluation of Commercial SAW Resonators by Means of a Direct and Reliable Equivalent-Circuit Extraction. Micromachines 2021, 12, 303. https://doi.org/10.3390/mi12030303
Gugliandolo G, Marinković Z, Campobello G, Crupi G, Donato N. On the Performance Evaluation of Commercial SAW Resonators by Means of a Direct and Reliable Equivalent-Circuit Extraction. Micromachines. 2021; 12(3):303. https://doi.org/10.3390/mi12030303
Chicago/Turabian StyleGugliandolo, Giovanni, Zlatica Marinković, Giuseppe Campobello, Giovanni Crupi, and Nicola Donato. 2021. "On the Performance Evaluation of Commercial SAW Resonators by Means of a Direct and Reliable Equivalent-Circuit Extraction" Micromachines 12, no. 3: 303. https://doi.org/10.3390/mi12030303
APA StyleGugliandolo, G., Marinković, Z., Campobello, G., Crupi, G., & Donato, N. (2021). On the Performance Evaluation of Commercial SAW Resonators by Means of a Direct and Reliable Equivalent-Circuit Extraction. Micromachines, 12(3), 303. https://doi.org/10.3390/mi12030303