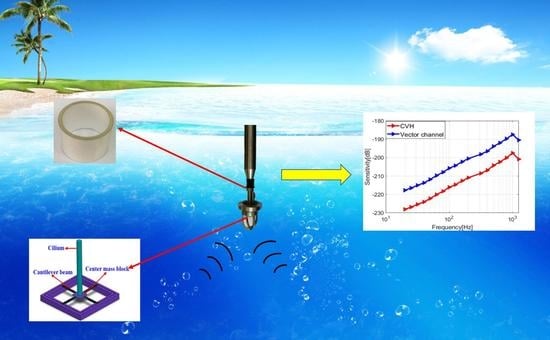
Design and Implementation of a Composite Hydrophone of Sound Pressure and Sound Pressure Gradient
Abstract
:1. Introduction
2. Directional Analysis
3. Design of the Composite Hydrophone
3.1. Design of Vector Channel
3.2. Sensing Principle of Scalar Channel
4. Theoretical Analysis
4.1. Sensitivity and Natural Frequency Analysis of Vector Channel
4.2. Scalar Channel Size Determination
5. Simulation Analysis
5.1. Stress Analysis on Beams of Vector Channel and Sensitivity Analysis of Piezoelectric Tube
5.2. Natural Frequency Analysis of Vector Channeland Piezoelectric Tube
6. Fabrication, Tests and Results
6.1. Fabrication
6.2. Tests and Results
7. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xu, J.H.; Zhang, X.L.; Fernando, S.N.; Chai, K.T.; Gu, Y.D. AlN-on-SOI platform-based micro-machined hydrophone. Appl. Phys. Lett. 2016, 109, 032902. [Google Scholar] [CrossRef]
- Kitsunai, H.; Kawashima, N.; Takeuchi, S.; Ishikawa, M.; Kurosawa, M.; Odaira, E. Development of miniature needle-type hydrophone with lead zirconate titanate polycrystalline film deposited by hydrothermal method. Jpn. J. Appl. Phys. 2006, 45, 4688–4692. [Google Scholar] [CrossRef]
- Foster, S.; Tikhomirov, A.; van Velzen, J. Towards a high performance fiber laser hydrophone. J. Light. Technol. 2011, 29, 1335–1342. [Google Scholar] [CrossRef]
- Ramesh, R.; Kara, H.; Bowen, C. Characteristics of piezoceramic and 3–3 piezocomposite hydrophones evaluated by finite element modelling. Comput. Mater. Sci. 2004, 30, 397–403. [Google Scholar] [CrossRef]
- Etienne, J.; Filipczyński, L.; Kujawska, T.; Zienkiewicz, B.; Filipczyńki, L. Electromagnetic hydrophone for pressure determination of shock wave pulses. Ultrasound Med. Biol. 1997, 23, 747–754. [Google Scholar] [CrossRef]
- Chen, H.; Shao, Z.; Hao, Y.; Rong, Q. A high-frequency hydrophone using an optical fiber microknot resonator. Opt. Commun. 2019, 446, 77–83. [Google Scholar] [CrossRef]
- Xu, J.; Chai, K.T.-C.; Wu, G.; Han, B.; Wai, E.L.-C.; Li, W.; Yeo, J.; Nijhof, E.; Gu, Y. Low-Cost, Tiny-sized MEMS hydrophone sensor for water pipeline leak detection. IEEE Trans. Ind. Electron. 2019, 66, 6374–6382. [Google Scholar] [CrossRef]
- Zaitsev, D.L.; Avdyukhina, S.Y.; Agafonov, V.M.; Bugaev, A.S.; Egorov, E.V. A molecular-electronic hydrophone for low-frequency research of ambient noise in the world ocean. Dokl. Earth Sci. 2018, 483, 1579–1581. [Google Scholar] [CrossRef]
- Pyo, S.; Kim, J.; Kim, H.; Roh, Y. Development of vector hydrophone using thickness–shear mode piezoelectric single crystal accelerometer. Sens. Actuators A Phys. 2018, 283, 220–227. [Google Scholar] [CrossRef]
- Leslie, C.B.; Kendall, J.M.; Jones, J.L. Hydrophone for measuring particle velocity. J. Acoust. Soc. Am. 1956, 28, 711–715. [Google Scholar] [CrossRef]
- McConnell, J.A. Analysis of a compliantly suspended acoustic velocity sensor. J. Acoust. Soc. Am. 2003, 113, 1395–1405. [Google Scholar] [CrossRef]
- Jin, M.; Ge, H.; Li, D.; Ni, C. Three-component homovibrational vector hydrophone based on fiber Bragg grating F-P interferometry. Appl. Opt. 2018, 57, 9195–9202. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Ma, R.; Li, F. High performance ultrathin fiber laser vector hydrophone. J. Light. Technol. 2011, 30, 1196–1200. [Google Scholar] [CrossRef]
- Kharat, D.K.; Mitra, S.; Akhtar, S.; Kumar, V. Polymeric piezoelectric transducers for hydrophone applications. Def. Sci. J. 2007, 57, 7–22. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Shi, B. A cylindrical hydrophone made of PVDF piezoelectric polymer and its performance. Sens. Actuators A Phys. 1993, 35, 231–234. [Google Scholar] [CrossRef]
- Fan, X.; Cao, Y.; Ha, K.; Kim, M.; Kang, H.W.; Oh, J. Fabrication of a PMN-PZT needle hydrophone for photoacoustic imaging. J. Acoust. Soc. Korea 2016, 35, 175–182. [Google Scholar] [CrossRef] [Green Version]
- Xue, C.; Chen, S.; Zhang, W.; Zhang, B.; Zhang, G.; Qiao, H. Design, fabrication, and preliminary characterization of a novel MEMS bionic vector hydrophone. Microelectron. J. 2007, 38, 1021–1026. [Google Scholar] [CrossRef]
- Fu, J.W.; Wang, X.Y. The compound vector hydrophone. In Proceedings of the 2014 Underwater Acoustic Confrontation Technology Academic Exchange Conference, Chengdu, China, 25–27 June 2014; p. 4. [Google Scholar]
- Liu, M.; Nie, L.; Zhang, G.; Zhang, W.; Zou, J. Realization of a composite MEMS hydrophone without left-right ambiguity. Sens. Actuators A Phys. 2018, 272, 231–241. [Google Scholar] [CrossRef]
- Xue, C.; Tong, Z.; Zhang, B.; Zhang, W. A novel vector hydrophone based on the piezoresistive effect of resonant tunneling diode. IEEE Sens. J. 2008, 8, 401–402. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, R.; Zhang, G.; Du, J.; Zhao, L.; Xue, C.; Zhang, W.; Liu, J. “Lollipop-shaped” high-sensitivity Microelectromechanical Systems vector hydrophone based on Parylene encapsulation. J. Appl. Phys. 2015, 118, 044501. [Google Scholar] [CrossRef]
- Jian, Z.M.; Zhang, G.J.; Liu, M.R.; Zhang, W.D. Microstructure optimization design of the MEMS bionic vector hydrophone. Micronanoelectron. Technol. 2014, 51, 576–582. [Google Scholar] [CrossRef]
- Teng, D.; Wang, Y.; Xie, K.K. Research on hydrophone based on tangentially polarized thin-walled piezoelectric circular tube. J. Shaanxi Norm. Univ. 2018, 46, 30–34. [Google Scholar] [CrossRef]
- Zhang, X.; Luo, L. Ship radiated noise detector when line spectrum parameters are unknown. J. Acoust. 2015, 40, 511–518. [Google Scholar]
- Zhen, S.; Yuan, W.; Liao, R. Acoustic Measurement and Testing Technology; Institute of Technology Press: Harbin, China, 1995. [Google Scholar]




















| Sizes | CVH | This Work |
|---|---|---|
| Length of beam (L) | 1000 μm | 1000 μm |
| Width of beam (b) | 120 μm | 120 μm |
| Thickness of beam (t) | 40 μm | 40 μm |
| Half-length of center block’s side (a) | 300 μm | 300 μm |
| Diameter of cilium (D) | 200 μm | 500 μm |
| Height of cilium(H) | 5000 μm | 5500 μm |
| Frequency (Hz) | Incident Angle (°) | Location Results (°) | Error (°) |
|---|---|---|---|
| 630Hz | 180 | 176 | 4 |
| 270 | 267 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Zhang, L.; Ji, S.; Yang, X.; Wang, R.; Zhang, W.; Yang, S. Design and Implementation of a Composite Hydrophone of Sound Pressure and Sound Pressure Gradient. Micromachines 2021, 12, 939. https://doi.org/10.3390/mi12080939
Zhang G, Zhang L, Ji S, Yang X, Wang R, Zhang W, Yang S. Design and Implementation of a Composite Hydrophone of Sound Pressure and Sound Pressure Gradient. Micromachines. 2021; 12(8):939. https://doi.org/10.3390/mi12080939
Chicago/Turabian StyleZhang, Guojun, Lansheng Zhang, Songxiang Ji, Xi Yang, Renxin Wang, Wendong Zhang, and Shie Yang. 2021. "Design and Implementation of a Composite Hydrophone of Sound Pressure and Sound Pressure Gradient" Micromachines 12, no. 8: 939. https://doi.org/10.3390/mi12080939
APA StyleZhang, G., Zhang, L., Ji, S., Yang, X., Wang, R., Zhang, W., & Yang, S. (2021). Design and Implementation of a Composite Hydrophone of Sound Pressure and Sound Pressure Gradient. Micromachines, 12(8), 939. https://doi.org/10.3390/mi12080939