Microkinetic Modeling of the Oxidation of Methane Over PdO Catalysts—Towards a Better Understanding of the Water Inhibition Effect

Abstract

Water, which is an intrinsic part of the exhaust gas of combustion engines, strongly inhibits the methane oxidation reaction over palladium oxide-based catalysts under lean conditions and leads to severe catalyst deactivation. In this combined experimental and modeling work, we approach this challenge with kinetic measurements in flow reactors and a microkinetic model, respectively. We propose a mechanism that takes the instantaneous impact of water on the noble metal particles into account. The dual site microkinetic model is based on the mean-field approximation and consists of 39 reversible surface reactions among 23 surface species, 15 related to Pd-sites, and eight associated with the oxide. A variable number of available catalytically active sites is used to describe light-off activity tests as well as spatially resolved concentration profiles. The total oxidation of methane is studied at atmospheric pressure, with space velocities of 160,000 h⁻¹ in the temperature range of 500–800 K for mixtures of methane in the presence of excess oxygen and up to 15% water, which are typical conditions occurring in the exhaust of lean-operated natural gas engines. The new approach presented is also of interest for modeling catalytic reactors showing a dynamic behavior of the catalytically active particles in general.

1. Introduction

Power-to-gas technologies, e.g., the combination of electrolysis and methanation for energy storage, gained lots of attention in the recent past [1,2]. Such processes may provide a sustainable solution to cover the increasing demand for renewable energy sources for both stationary and mobile applications, and may alleviate the anthropogenic climate change. Moreover, its advantageous hydrogen-to-carbon ratio also makes methane a highly attractive energy carrier, hence natural gas (NG) engines could play an important role in the near future [3]. Despite high fuel efficiency and comparatively low raw emissions, efficient exhaust gas after-treatment systems of natural gas engines are indispensable nowadays, especially in the mobility sector [4,5]. Emissions of CH₄, with over 20 times higher global warming potential compared to CO₂ [6], need to be avoided under any circumstances.

In the context of the catalytic total oxidation of methane, particularly PdO-based catalysts supported on alumina show high activities in the low temperature regime between 600 K and 700 K under lean (oxygen excess) operation [7,8]. In comparison to stoichiometric operation, whereby a three-way catalytic converter can be applied for emission control, lean operation would further increase the efficiency and therefore reduce the fuel consumption of natural gas engines. Despite extensive research efforts, there is still no adequate catalytic after-treatment system available for the reduction of methane emissions from lean operated NG engines. The best catalytic system found so far, PdO-based catalysts, does not achieve the desired long-term activity in the presence of water, which is always formed in combustion and therefore an intrinsic component of the exhaust gas. The underlying mechanism of the water deactivation effect is still not fully understood. According to Ciuparu et al. [9,10], hydroxyl accumulation on the surface of the active particle leads to the observed activity shift towards higher temperatures and continuous deactivation, which is even more pronounced with steam present in the feed gas.

Furthermore, methane oxidation follows the Mars–van Krevelen mechanism [11,12], hence the overall activity strongly depends on the size of the noble metal particles [13,14]. The catalytic behavior may even change during the course of the reaction due to the reversible phase transformation of PdO and Pd and the combined effect of morphology and structural changes [15]. Structural differences of the PdO-phase also differ in the process of methane oxidation, with PdO(100) being the thermodynamically most stable facet, whereas PdO(101) shows the comparatively lowest energy barrier for methane activation [16,17]. Amongst these properties, the catalyst is moreover influenced by the support material [18,19] and by further noble metal dopants such as platinum [20,21]. Furthermore, Lott et al. recently described an enhanced oxidation performance for pre-reduced PdO catalysts in the presence and absence of externally dosed water, pointing to a strong dependence of the catalytic activity on the catalyst history [22,23]. All the mentioned aspects result in the complex non-linear behavior of the catalytic PdO system.

In order to capture the dynamics and the effect of externally dosed water on the catalytic system, the combination of systematic experiments with microkinetic modeling can help to understand the physical interplay between transport phenomena, kinetics, and surface state of the noble metal particles. The basis of this study are surface reaction mechanisms that were recently developed for the oxidation of methane over reduced [24] and oxidized Pd-based catalysts [25]. With both of these mechanisms, the hysteresis behavior of PdO catalysts [26,27], which was attributed to different rates of CH₄ oxidation upon cooling and heating of the system, could be explained.

In this study, we propose an approach that is able to also model the instant inhibition effect of water on the catalytic total oxidation of methane over palladium-based catalysts. Aside from the instant loss in activity due to steam, the catalyst also experiences long-term deactivation due to thermal aging for instance, which is not in the focus of the model development of this study.

A set of flow reactor experiments was conducted using powder catalysts to capture the water inhibition effect, which is fully developed with increasing amount of externally dosed water. Based on consecutive conclusions drawn from the systematic experiments, the recently published microkinetic model of Stotz et al. [25] was extended to better capture the water inhibition effect. In their study Stotz et al. [25] denoted dissociative adsorption of methane via hydrogen abstraction over Pd-O active site-pairs as the rate controlling step. The microkinetic model in their formulation partly captures an observerd water inhibition effect by taking a site blocking process due to formation of hydroxyl species as well as competing reversible H₂O/OH adsorption on available catalyst sites into account. However, the water inhibition on this microkinetic level is still underestimated, making further model development inevitable. Hereby, the impact on the overall catalytically active surface is assessed qualitatively for different concentrations of externally dosed steam, which contributes to understanding the blocking mechanism on a molecular level of the active particles. Finally, the optimized model can also describe the catalytic activity tests and spatially resolved concentration profiles obtained for a monolithic catalyst sample.

2. Results and Discussion

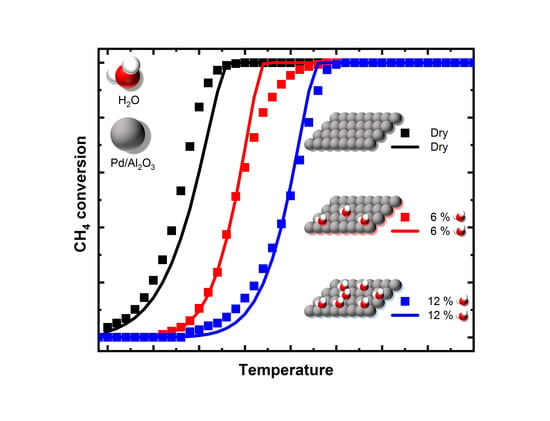
2.1. Experimental Results

The experimental results reported in this section are the basis the necessary model extension to capture the effect of water inhibition on catalytic activity. A summary of the catalyst characterization results is given in

Table 1. Results of the catalyst characterizations obtained from N₂-physisorption, chemisorption, transmission electron microscopy (TEM) and elemental analysis.

Method	PdO/Al2O3
BET surface area/m2 g−1	176
Pore volume/mL g−1	0.46
Noble metal dispersion/%	28
Mean particle diameter (TEM), as prepared catalyst/nm	1.5
Mean particle diameter (TEM), aged catalyst/nm	2.5
Noble metal loading/wt.%	2.23

. To investigate the influence of externally dosed water, the catalytic conversion of methane is measured in light-off activity tests at different steam concentrations. The results for a dry reaction mixture (3200 ppm CH₄, 10% O₂ in N₂, GHSV = 140,000 h⁻¹) and with water added in the concentrations of 1%, 2%, 3%, 6%, 9%, 12%, and 15% are depicted in Figure 1.

The effect of water in the feed gas is clearly visible: with increasing water concentration, the activity of the catalyst was decreased and therefore the conversion of CH₄ was shifted towards higher temperatures. While in the dry reaction mixture 50% conversion (T₅₀) are achieved at 578 K and nearly full conversion (T₁₀₀) is reached at 630 K, already 1% of externally dosed water leads to a T₅₀-temperature shift of approximately 60 K. The inhibition becomes even more severe at higher steam concentration, resulting in a shift of 143 K for T₁₀₀ when 15% water are added. While the general slope of the light-off curve is only slightly influenced by the inhibition effect, catalytic activity is continuously shifted towards higher temperatures. To show that the inhibition effect on the catalytically active particles is already fully developed within the water concentrations of the experiments, the temperature shifts of T₅₀ and T₁₀₀ are summarized in Figure 2.

The effect of steam on the catalytic methane conversion evolves for T₅₀ and T₁₀₀ in a similar manner. The sharpest temperature increase is found for low steam concentrations between 1–3% [28]. Nevertheless, the effect emerges and the temperature shift doubles from 60 K at 1% externally dosed water to more than 140 K at 15% steam for T₅₀.

However, further long-term experiments revealed an additional mechanism resulting in catalyst deactivation. The powder catalyst was aged for 35 h at 823 K in a reactive atmosphere of 3200 ppm CH₄, 10% O₂, 15% H₂O in N₂. Significant particle sintering is observable in the presence of 15% H₂O at elevated temperatures compared to the freshly prepared catalyst, resulting in an activity loss of over 50%. Figure 3 shows TEM images of an as prepared fully oxidized powder catalyst used for every light-off measurement and one of the aged PdO/Al₂O₃ sample and the associated particle size distribution in Figure 4, that are present in the oxidized PdO. The as prepared catalyst sample in the left image of Figure 3 shows small noble metal particles that are homogenously distributed above the whole surface of the support material, resulting in a mean particle diameter of 1.5 nm. In contrast, the TEM image of the aged catalyst shows bigger agglomerates all over the depicted surface. Additionally, the smaller bright reflexes caused by the former homogenously distributed noble metal particles disappeared, leading to a new mean particle diameter of 2.5 nm and therefore a smaller catalytically active surface area. These results indicate that besides the instant water inhibition effect steam present in the exhaust gas is able to trigger particle sintering, thus leading to catalyst deactivation on larger time scales. In order to ensure a clear differentiation between an instant inhibition, as predominantly observed in the light-off tests, and long-term deactivation that happens over hours at elevated temperatures and which is presumably caused by a similar, yet slightly different mechanism, each light-off test was run with a fresh catalyst sample prepared in the reactor. This procedure ensured that only the first effect of the hydrous gas atmosphere is captured by the set of experiments. Thus, the following work focuses on modeling the observed instant behavior with externally dosed water in the exhaust gas. The developed microkinetic mechanism is further used to develop insights regarding the catalytically active surface during the total oxidation of methane.

2.2. Modeling the Water Inhibition Effect

The modeling approach presented in this study is based on our previously published microkinetic mechanism [25]. By extending the previous model we are now also able to capture the water inhibition effect more precisely. This adaption allows to accurately model the influence of steam on the system by introducing a quantitative description of the initially available catalytically active surface. The modeling results with the input parameters given in

Table 2. Summary of the experimental parameters and model input.

Parameter	Value	Unit
CH4	3200	ppm
O2	10	Vol.%
N2	75–90	Vol.%
H2O	0–15	Vol.%
GHSV	140,000	h−1
Pressure p	1000	kPa
Length of the packed bed L	15	mm
Inner diameter of the reactor DL	6	mm
Particle size (sieve fraction) D	125–250	μm
Catalytic to geometric surface area ratio Fcat,geo	510	-

are shown in Figure 5.

Up to this point, all parameters are set by the experiment. The model parameter F_cat,geo represents the dimensionless accessible catalytically active surface area and was determined as described in the computational part by the mean average particle size that was derived by TEM. The accuracy of the derived calculation is validated with the dry case, which is the light-off measurement without externally dosed water (Figure 5). The model predicts the ignition of the reaction around 500 K as well as T₅₀ and T₁₀₀ rather well. The further model modification to capture the water inhibition effect relies on an altered catalytically active surface area with different amounts of externally dosed water.

The variations in accessible surface sites were considered when fitting F_cat,geo to T₅₀ of the light-off measurements, to capture ignition of the reaction. With this procedure, all experiments are described as accurately as the dry case (Figure 5). The modeling work focuses on T₅₀ for two reasons. Firstly, the initial start of the activity is better captured in the low temperature regime, which is the main advantage of using PdO-based catalysts in the first place. Secondly, at full conversion and higher temperatures with rather fast chemical reactions, other phenomena such as transport limitation [29] or advanced aging of the catalyst may occur. With a temperature ramp of 3 K min⁻¹, the time on stream would differ about 47 min for the experiment with 1% compared to the 12% of externally dosed water, resulting in incomparable performance results. However, a slight difference is noticeable for smaller water concentrations between 1% and 3%. Although the average H₂O concentration met the set value in this range, minor oscillations around the mean value due to less precise water dosage by the controlled evaporation mixer occurred, which are optimized for a higher water dosage. Additionally, it might be reasonable to accept a higher water inhibition effect at elevated temperatures with increasing steam concentration, however, the impact at lower temperatures will be more severe due to persistent blockage of the surface. This combination may contribute to the minor discrepancies in the experimental data. With the applied modification, the influence of the gaseous environment on the noble metal particles can be calculated, resulting in different surface areas for the range of water concentrations in the experiments as depicted in Figure 6. The change in the model input parameters follows the trend for the water inhibition effect, the methane oxidation is decreasing. While with 1% externally dosed water already 50% of the surface is blocked, this effect enlarges up to 87.8% at a water concentration of 15%. To our best knowledge, this is the first attempt in literature to find a direct quantitative correlation between the instant water inhibition effect on methane oxidation and the accessible catalytic surface area. With increasing amount of externally dosed water, clearly less catalytically active surface area is accessible for the methane oxidation. For this model adaptation, thermodynamic consistency is still guaranteed, because the microkinetic mechanism remains uniform, which is the main advantage of the chosen method. Whether the active particles react to the gaseous environment with a different active facet or shape, i.e., as observed for Zn-O-Cu catalysts for methanol synthesis [30,31,32], or in combination with hydroxyl formation [33], solely a change in F_cat,geo accounts for a different catalytic activity.

Ideally, the uniform microkinetic mechanism covers experiments with a wide variety of reaction conditions and a broad range of gas concentrations. In the following, the model is used to describe methane conversion as observed in monolith experiments [24], which were conducted for the development of the initial PdO-based model with a fixed dispersion. The input parameters as well as the parameters of the monolithic catalyst are set by the experiment and listed in the publication in great detail [24]. The results for the fixed dispersion value and the modified model are compared in Figure 7.

While the model with fixed dispersion captures the overall slope rather well, it underestimates the pronounced activity shift towards higher temperatures, which is clearly visible for the experimental data. The assumption that over 80% of the active surface is blocked at a water concentration of 6% results in good accordance with experimental data. The start of the ignition as well as T₅₀ is accurately predicted by the model and also in the range of full conversion only minor discrepancies are noticeable. Furthermore, the two simulated light-off curves in the presence of 6 and 12% H₂O for the modified model are separated by 32 K at T₅₀, which is more realistic compared to the experimental temperature gap of 44 K. For the monolith light-offs, a pronounced diffusion is partly prevented by the geometry, mass transfer limitation is less significant in packed bed experiments due to the filling of the reactor. A shape modification or sintering of the noble metal particles with an associated smaller catalytic surface area as for instance observed after aging the PdO/Al₂O₃ catalyst in the presence of 15% H₂O for 35 h cannot explain the water inhibition as described in the modeling results. Including the new mean diameter of 2.5 nm of the sintered particles, obtained for the aged catalyst, in trying to capture the water inhibition effect for the modeled light-off experiment still provides an overestimated catalytic activity compared to the experimental results as shown in Figure 8. The model with the fixed dispersion as well as the new input parameter including the sintered noble particles clearly overestimate the catalytic activity in the presence of 15% H₂O. In this context, the long-term experiment rather reveals that the influence of externally dosed water is able to trigger particle sintering and changes in morphology. However, this aging mechanism differs from the instant inhibition and can therefore only partly explain the observed results. It is proposed that the values chosen for modeling originate from a combination of a minor change in dispersion caused by particle sintering, possibly going along with a shape change of active particles when steam is present in the exhaust gas. Additionally, the accumulation of hydroxyl and other species on the surface block active sites, further influencing the catalytic activity. Nevertheless, the significance and accuracy of the current approach is undeniable. For this reason, the modified model is further used to simulate spatially resolved concentration profiles of the water inhibition effect and compared to experimental results, which demonstrates how applicable the model is.

2.3. Modeling Spatially Resolved Concentration Profiles

The extended model is further used to describe experimental monolith data for methane oxidation that were conducted in a setup dedicated for spatial profiling (SpaciPro) [34,35,36]. First, light-off measurements justify the applicability of the model. Subsequently, conducted temperature and concentration profiles inside a channel of the monolith are modeled and compared to the results of the measurements.

The results for the light-off measurements in the SpaciPro setup in the absence and presence of 6% and 12% water are shown in Figure 9. The overall activity of the catalytic system is in good accordance to the light-off tests of Figure 7. Whereas the gas hourly space velocity (GHSV) is halved, the methane concentration is increased from 1000 ppm to 3200 ppm, leading to a T₅₀ temperature of 608 K, which is 20 K above the dry experiments [25]. The instant water inhibition effect on the catalytic activity is also captured by the extended model. Since no TEM images were available for the noble metal particles, assumptions of Stotz et al. [25] were used to correlate the surface of the reduced palladium species determined by chemisorption to the initial surface of the PdO particles. Taking this into account, the ignition of the total oxidation and T₅₀ is described in sufficient detail. Thus, the lower GHSV slightly minimizes the effect of internal mass transfer limitation, leading to better accordance of the general light-off slope at elevated temperatures for 12% externally dosed water.

Three different approaches are compared when modeling the spatially resolved concentration profile obtained with a monolithic sample. Figure 10a shows the experimental concentration profile inside a catalytic channel in the absence of water, as well as the isothermal, adiabatic and discretized simulation, that uses the associated temperature profile (black line) depicted in Figure 10b as an input for the channel wall temperature at the given axial position.

The isothermal simulation for a reactor temperature of 648 K clearly underestimates the methane conversion inside the monolith channel. In the light-off simulation full conversion is achieved after 660 K. Therefore, the spatially resolved simulation is leading to an end of pipe concentration of 0.023% CH₄, which is a conversion of 92.8%. In contrast, the adiabatic simulation slightly overestimates the catalytic performance of the system. Full conversion is achieved within the first 5 mm of the channel that has a total length of 19 mm. The increased activity originates from an overestimated heat development that is predicted by the adiabatic simulation in Figure 10b. After 6 mm inside the channel, the gas and wall temperature reach the maximum temperature of 730 K. Compared to the experimental results, the temperature profile shows a significant hotspot with 690 K after 9 mm. Using this temperature profile as the model input ensures the most accurate results in the so-called discretized simulation, which is a stepwise isothermal simulation.

It should be noted that, according to Hettel et al. [37], the intrusion of the capillary affects the flow inside the channel leading to an increased residence time and therefore higher catalytic conversion. With respect to the results presented in this paper, this means that the monitored conversion is higher compared to the remaining monolith channels, thus the most representative profile is a combination of the isothermal and discretized simulation.

Finally, the water inhibition effect was also investigated in a spatially resolved manner. Figure 11a shows the concentration profile for a 19 mm long monolith in a gas mixture consisting of 3200 ppm CH₄, 10% O₂ and 12% H₂O in N₂ at 798 K, which results in full conversion. In the simulations, irrespective of the chosen approach, full conversion is achieved within the framework of the modified model that contains the water inhibition effect. Although heat development is again overestimated as shown in Figure 11b, the adiabatic simulation is the best description, with the highest temperature of 877 K achieved at an axial position of 3 mm, whereas in the experiment, the hotspot formed at 14 mm with a temperature of 850 K. The discretized simulation predicts full conversion after 12 mm, whereas methane is fully converted only at the end of the catalytic channel in the isothermal simulation. The results can be further interpreted in the light of the conclusions from the activity measurements: at higher temperatures methane oxidation is partly limited by mass transfer [26] and not by the rather fast chemical reaction in the presence of steam.

Thus, an increased gas residence time is beneficial for further conversion, which is observable in the experimental profiles compared to the simulations. Given the fact that minor discrepancies are visible in the initial light-off experiment in Figure 9, the accuracy of the spatially resolved concentration profile is fairly sufficient.

Again, for the overall activity of the monolith, a combination of the flatter course for the discretized and isothermal simulation is the best representation for the conditions of the experiments. Due to the filigree and thin capillary technique of the SpaciPro setup, the concentration profiles were axially aligned to match a monolith entrance concentration of 3200 ppm CH₄.

3. Materials and Methods

3.1. Experimental

The PdO/Al₂O₃ catalyst was prepared by incipient wetness impregnation (IWI) with a target noble metal loading of 2.4 wt%. After impregnating γ-Al₂O₃ (SASOL) with an aqueous solution of tetraaminepalladium(II)-nitrate (Chempur, 3.3 wt% Pd) the received powder catalyst was first dried at 70 °C for 1 h and subsequently calcined at 550 °C for 5 h. The noble metal loading was determined by elemental analysis (inductively coupled plasma optical emission spectrometry, ICP-OES) to be 2.23 wt%. Prior to the N₂-physiosorption measurement, the surface was cleaned by degassing the catalyst for 2 h at 300 °C. Afterwards, the BET-measurement [38] was conducted in a BELSORP Mini II analyser (MicrotracBEL). Scanning transmission electron microscopy (STEM) images were obtained with a FEI OSIRIS microscope (200 kV electron energy) at the Laboratory for Electron Microscopy (LEM, KIT, Karlsruhe, Germany). Analyzing over 400 noble metal particles with the software package Fiji in high angle annular dark field scanning (HAADF) and bright field mode (BF) led to the particle size distribution shown in Figure 4.

3.2. Activity Tests

The as prepared catalyst was sieved to a particle fraction of 125–250 μm to minimize internal mass transfer limitation [39]. Subsequently, 300 mg of this fraction was diluted with 700 mg SiO₂ of the same particle size to prevent local hotspots. A quartz glass tubular reactor (inner diameter: 6 mm) was loaded with the powder. The resulting fixed packed bed had a length of approximately 1.5 cm. For every conducted activity test, freshly prepared catalyst was used to capture the instant water inhibition effect, rather than combined aging phenomena. The light-off measurements were conducted in the Exhaust gas center Karlsruhe with a gaseous environment of 3200 ppm CH₄, 10% O₂, and different amounts of externally dosed water in balance N₂. Mass flow controllers (MFC, Bronkhost) allowed for the precise dosage of the different gases, whereas steam was dosed with a controlled evaporator and mixer system (CEM, Bronkhost). Gas concentrations were measured end of pipe with a Fourier-transform infrared spectrometer (FTIR, Multigas MG2030, MKS) and the entire setup was controlled with an in-house developed LabView software tool. Heating was realized with Eurotherm controllers to conduct light-off cycles with a temperature ramp of 3 K min⁻¹ between 500 K and 825 K. An initial degreening of the catalyst at 825 K in a reactive gas environment in the absence of water (3200 ppm CH₄, 10% O₂ in N₂) guaranteed identical starting conditions. All activity tests were conducted with a constant gas hour space velocity (GHSV) of 140,000 h⁻¹.

3.3. Spatially Resolved Profiles

Spatially resolved concentration profiles were recorded in monolith experiments with a setup dedicated for spatial profiling (SpaciPro) [34,35,36]. The honeycomb structure with 400 cpsi had a total noble metal loading of 100 g ft⁻³. The monolith coating was realized by applying a slurry containing the catalyst and AlO(OH) (Disperal P2, SASOL) as a binder via dip coating. The resulting monolith sample was 19 mm long with a diameter of 18 mm. The in-situ axial concentration profiles were obtained by inserting a small capillary (outer diameter 170 µm, inner diameter 100 µm) into a single central monolithic channel that was connected with a mass spectrometer (Hiden Analytical, HPR20). For the temperature profiles a type K thermocouple (diameter 250 µm) was used. Both measuring instruments were pulled out of the monolith channel by an electric motorized linear stage (Zaber Technologies, T-LSM 100A). For a detailed description of the setup the reader is referred to previous studies [34].

3.4. Computational Methods—Reactor Model

The recently published microkinetic model developed by Stotz et al. [25] was applied to isothermally model the oxidation of methane to carbon dioxide and water. The steady-state species concentration profiles were obtained using the software package DETCHEM^TM, more specifically the code DETCHEM^CHANNEL [40]. Monolith and packed bed experiments were simulated with the same code package and are thus directly comparable. The porosity of the latter is taken into account using the formula proposed by Pushnov [41] leading to an imaginary pathway through the reactor, which is synonymous with modelling a channel of monolith experiments. With the pipe diameter $D$, which is at least twice the particle size $d_p$ (sieve fraction) and the height of the column being at least 20 times $d_p$ the porosity ϵ can be estimated with

$$ϵ=\frac{A}{{\frac{D}{dp}}^n}+B$$

(1)

where $A$, $B,$ and $n$ are constants given by Pushnov [41]. To gain physically meaningful input parameters for reliable simulations the channel diameter was set to the diameter of the catalyst particles. A steady-state two-dimensional flow is computed using the boundary-layer approximation. Fundamentally, this approach relies on the governing partial differential equations of mass conservation, axial momentum conservation, radial momentum, and energy and species continuity. These are defined in the following.

Mass conservation:

$$ϵ=\frac{A}{{\frac{D}{dp}}^n}+B$$

(2)

Axial momentum conservation:

$$\frac{\partial \left(r\rho u\right)}{\partial z}+\frac{\partial \left(rpv\right) }{\partial r}=0$$

(3)

Radial momentum continuity:

$$\frac{\partial \left(r\rho u^2\right)}{\partial z}+\frac{\partial \left(rpuv\right)}{\partial r}=-r\frac{\partial p}{\partial z}+\frac{\partial }{\partial r}\left(\mu r\frac{\partial u}{\partial r}\right)$$

(4)

Energy continuity:

$$\frac{\partial \left(r\rho uh\right)}{\partial z}+\frac{\partial \left(rpvh\right)}{\partial r}=u\frac{\partial p}{\partial z}+\frac{\partial }{\partial r}\left(\lambda r\frac{\partial T}{\partial r}\right)-\frac{\partial }{\partial r}{\displaystyle \sum }_{i}r{j}_i{h}_i$$

(5)

Species continuity:

$$\frac{\partial \left(r\rho u{Y}_i\right)}{\partial z}+\frac{\partial \left(rpv{Y}_i\right)}{\partial r}=\frac{\partial }{\partial r}\left(r{j}_i\right)+r \dot{w_i}$$

(6)

Ideal gas equation of state:

$$p=\frac{p\overline{M}}{RT}$$

(7)

In the equations above, $z$. denotes the axial, $r$ the radial coordinate respectively, $\rho$ the density, $u$ the axial and $v$ the radial velocity component. Additionally, $h$ is the enthalpy, $p$ the pressure, $\lambda$ the thermal conductivity and $T$ the corresponding temperature. $Y$ describes the mass fraction, $j$ the radial diffusion flux, and $\dot{w_i}$ the gas phase production rate of the species $i$. In the ideal gas equation of state $\overline{M}$ is the mean molecular weight of the gas-mixture and $R$ the universal gas constant. As a model input parameter, the inlet flow velocity had to be calculated from the measured experimental volume flux that was adjusted to the correlated gas inlet temperature. Furthermore, the simulations based on monolith experiments used the effectiveness model to represent limited diffusion behavior inside the channel.

Owing to the comparable low temperatures of the oxidation reaction, gas phase reactions typically do not occur, hence only surface reactions are embedded in the elementary-step based reaction mechanism. The chemical source term ${\dot{s}}_i$ of the surface species $i$ is described within approximations of the mean-field theory.

$${\dot{s}}_i=k_{f,k}{\displaystyle \prod }_{j=1}^{N_g+N_s}{c}_j^{v_{jk}^{\prime }}-k_{r,k}{\displaystyle \prod }_{j=1}^{N_g+N_s}{c}_j^{v_{jk}^{″}}$$

(8)

Herein, $v_{jk}^{\prime }$ and, $v_{jk}^{″}$ are the stoichiometric coefficients of all species $j$ involved in step $k$ for the forward reaction $k_{f,k}$ and the backward reaction $k_{r,k}$ respectively. The species concentrations are represented by $c_j$, whereas $N_s$ and $N_g$ are the surface and gas-phase species also involved in adsorption and desorption processes. Subsequently, the surface coverages ${\theta }_i$ in steady-state yields into

$${\theta }_i=c_i\frac{{\sigma }_i}{\mathsf{\Gamma }}$$

(9)

where ${\sigma }_i$ is the number of occupied surface sites and $\mathsf{\Gamma } =3.553\ast {10}^{-9}mol c{m}^{-2}$ [25] is the surface site density of PdO. Furthermore, a modified Arrhenius expression is used to describe the rate coefficients of the surface reactions that accounts for the coverage dependency ${ϵ}_i$ of the activation energy.

$$k_k=A_k{T}^{{\beta }_k}\exp \left[-\frac{E_{a,k}}{RT}\right]\ast {\displaystyle \prod }_{i=1}^{N_s}\exp \left[\frac{{\nu }_{i,k}{ϵ}_i{\theta }_i}{RT}\right]$$

(10)

Equation (10) uses the pre-exponential factor $A_k$ which is temperature corrected with $T^{{\beta }_k}$. Adsorption reactions are modelled with sticking coefficients $s_i^0$ that calculate rate constants as

$$k^{ads}=\frac{s_i^0}{{\mathsf{\Gamma }}^{n_k}}\sqrt{\frac{RT}{2\pi M_i}}$$

(11)

Here, the exponent $n_k$ accounts for the molecular adsorption with the value of 1 for molecular adsorption and a dissociative adsorption with $n_k=2$. Additionally, the mechanism used in this study exhibits full thermodynamic consistency, which means that the equilibrium is represented in the limit of an infinite time scale for all elementary steps being reversible. The procedure has been described in great detail in the literature [42]. Particularly, the model input parameter $F_{cat,geo}$ is focus of the study, which is the quotient of the catalytically active area $A_{cat}$ and the geometric area $A_{geo}$.

$$F_{cat,geo}=\frac{A_{cat}}{A_{geo}}$$

(12)

The latter is given by the product of the converted geometric surface that are the channel diameter $D$ and the length of the catalyst $L$.

$$A_{geo}=\pi DL$$

(13)

$A_{cat}$ can be calculated with the mean particle diameter ${\overline{d}}_{NP}$ determined by TEM images and the hemispherical particle assumption [43]

$$A_{cat}=\frac{6m_{PdO}}{ {\overline{d}}_{NP}{\rho }_{PdO}}$$

(14)

The used mass of PdO is denoted by $m_{PdO}$ with the density ${\rho }_{PdO}$.

3.5. Chemical Model

Our group recently published the chemical model used in this study, shown in Appendix A

Table A1. Kinetic parameters of the two-site mean field reaction mechanism for methane oxidation over PdO in the form of the modified Arrhenius expression. The mechanism is fully thermodynamically consistent. The coordinatively unsaturated Pd sites are denoted as (a), whereas the lattice oxygen sites of PdO (1 0 1) are represented by (b) [25].

Nr.	Adsorption/Desorption Reaction	${\mathit{s}}^{\mathbf{0}}\mathbf{/}\mathbf{-}$	${\mathit{\beta }}_{\mathit{f}}\mathbf{/}\mathbf{-}$	${\mathit{E}}_{\mathit{a}\mathbf{,}\mathit{f}}\mathbf{/}\mathit{k}\mathit{J}\mathit{m}\mathit{o}{\mathit{l}}^{\mathbf{-}\mathbf{1}}$	${\mathit{A}}_{\mathit{r}}\mathbf{/}\mathit{m}\mathit{o}\mathit{l}\mathbf{,} \mathit{c}\mathit{m}\mathbf{,} \mathit{s}$	${\mathit{\beta }}_{\mathit{r}}\mathbf{/}\mathbf{-}$	${\mathit{E}}_{\mathit{a}\mathbf{,}\mathit{r}}\mathbf{/}\mathit{k}\mathit{J}\mathit{m}\mathit{o}{\mathbf{l}}^{\mathbf{-}\mathbf{1}}$
R1	CH4(g) + (a) + (b)⇄ CH3(a) + H(b)	4.582∙10− 02	−0.001	33.155	1.034∙10+ 21	0.003	106.18
R2	CH4(g) + OH(a) + (a)⇄ CH3(a) + H2O(b)	1.510∙10− 02	0.001	28.860	7.071∙10+ 19	−0.004	104.259
R3	CH4(g) + O(a) + (a)⇄ CH3(a) + OH(a)	3.082∙10− 02	0.007	26.234	2.695∙10+ 20	−0.029	192.865
R4	O2(g) + (a) ⇄ O2(a)	5.710∙10− 02	0.0	0.0	6.702∙10+ 15	−0.031	63.541
R5	O2(g) + vac(b) ⇄ O2(b)	5.710∙10− 02	0.0	0.0	7.024∙10+ 15	−0.027	159.975
R6	H2O(g) + O(a) + (a) ⇄ 2OH(a)	1.400∙10− 01	0.0	0.0	3.307∙10+ 20	0.013	191.178
R7	H2O(g) + (a) ⇄ H2O(a)	1.400∙10− 01	0.0	0.0	6.297∙10+ 12	0.045	99.946
R8	CO2(g) + (a) ⇄ CO2(a)	4.910∙10− 02	0.0	0.0	4.087∙10+ 14	0.029	65.097
Nr.	Surface Reaction	${\mathit{A}}_{\mathit{f}}\mathbf{/}\mathit{m}\mathit{o}\mathit{l}\mathbf{,} \mathit{c}\mathit{m}\mathbf{,} \mathit{s}$	${\mathit{\beta }}_{\mathit{f}}\mathbf{/}\mathbf{-}$	${\mathit{E}}_{\mathit{a}\mathbf{,}\mathit{f}}\mathbf{/}\mathit{k}\mathit{J}\mathit{m}\mathit{o}{\mathit{l}}^{\mathbf{-}\mathbf{1}}$	${\mathit{A}}_{\mathit{r}}\mathbf{/}\mathit{m}\mathit{o}\mathit{l}\mathbf{,} \mathit{c}\mathit{m}\mathbf{,} \mathit{s}$	${\mathit{\beta }}_{\mathit{r}}\mathbf{/}\mathbf{-}$	${\mathit{E}}_{\mathit{a}\mathbf{,}\mathit{r}}\mathbf{/}\mathit{k}\mathit{J}\mathit{m}\mathit{o}{\mathit{l}}^{\mathbf{-}\mathbf{1}}$
R9	CH3(a) + (b) ⇄ CH3(b) + (a)	1.494∙10+ 22	0.008	131.139	2.441∙10+ 23	0.008	181.201
R10	CH3(b) + O(a) ⇄ CH2(b) + OH(a)	1.250∙10+ 22	0.012	33.366	1.855∙10+ 22	−0.012	303.074
R11	CH3(a) + OH(a) ⇄ CH2(b) + H2O(a)	1.398∙10+ 22	−0.004	33.193	1.111∙10+ 22	0.004	221.667
R12	CH3(a) + O(a) ⇄ CH2OH(a) + (a)	3.534∙10+ 21	0.016	30.953	2.466∙10+ 23	−0.016	333.447
R13	CH3(a) + OH(a) ⇄ CH2(a) + H2O(a)	2.014∙10+ 21	0.004	73.228	1.175∙10+ 22	−0.004	116.851
R14	CH2(a) + OH(a) ⇄ CH2OH(a) + (a)	3.420∙10+ 21	−0.004	12.581	2.191∙10+ 22	0.004	180.219
R15	CH2OH(a) + (b) ⇄ CH2O(b) + H(b)	1.917∙10+ 22	0.012	12.654	3.348∙10+ 20	−0.012	57.646
R16	CH2O(a) + OH(a) ⇄ CHO(a) + H2O(a)	5.608∙10+ 21	0.012	51.570	2.119∙10+ 22	−0.012	192.230
R17	CHO(a) + OH(a) ⇄ CO(a) + H2O(a)	5.921∙10+ 22	0.008	65.968	8.990∙10+ 21	−0.008	267.530
R18	CH3(a) + (b) ⇄ CH2(a) + H(b)	1.827∙10+ 21	0.0	123.976	5.137∙10+ 22	0.0	165.224
R19	CH2(a) + (b) ⇄ CH2(b) + (a)	1.257∙10+ 22	0.0	13.103	2.797∙10+ 22	0.0	198.017
R20	CH2(a) + (b) ⇄ CH(a) + H(b)	3.793∙10+ 22	0.008	112.541	2.987∙10+ 22	−0.008	163.159
R21	CH(a) + (b) ⇄ CHO(a) + vac(b)	2.103∙10+ 21	0.008	24.821	1.218∙10+ 21	−0.008	215.219
R22	CH2(b) + (a) ⇄ CH2O(a) + vac(b)	2.155∙10+ 22	0.008	91.22	2.425∙10+ 20	−0.008	9.038
R23	CH2O(a) + (b) ⇄ CHO(a) + H(b)	3.274∙10+ 21	0.008	69.676	5.962∙10+ 22	−0.008	207.964
R24	CHO(a) + (b) ⇄ CO(a) + H(b)	1.088∙10+ 32	0.004	55.610	7.956∙10+ 22	−0.004	254.800
R25	CHO(a) + (b) ⇄ CHO(b) + (a)	2.746∙10+ 22	0.018	76.549	6.754∙10+ 21	−0.018	106.611
R26	CHO(b) + (a) ⇄ CO(b) + H(a)	2.732∙10+ 12	−0.002	141.937	2.123∙10+ 21	0.002	263.113
R27	CO(a) + (b) ⇄ (a) + CO(b)	1.313∙10+ 12	0.011	33.868	2.212∙10+ 21	−0.011	16.262
R28	CO(b) + (a) ⇄ CO2(a) + vac(b)	1.40∙10+ 21	0.010	42.023	9.554∙10+ 20	−0.010	78.477
R29	H(b) + (a) ⇄ OH(a) + vac(b)	1.886∙10+ 22	0.0	137.8	4.222∙10+ 21	0.0	27.9
R30	O2(a) + (a) ⇄ O(a) + O(a)	3.815∙10+ 22	0.005	174.961	1.744∙10+ 21	−0.005	59.139
R31	O(b) + (a) ⇄ O(a) + (b)	2.380∙10+ 22	0.027	116.625	1.797∙10+ 21	−0.027	107.875
R32	O(a) + vac(b) ⇄ (a) + (b)	8.012∙10+ 21	0.020	48.597	1.387∙10+ 22	−0.020	252.103
R33	O2(a) + vac(b) ⇄ O(a) + (b)	1.196∙10+ 24	0.025	81.408	9.469∙10+ 22	−0.025	169.092
R34	H(b) + (a) ⇄ H(a) + (b)	6.133∙10+ 22	0.002	148.173	9.505∙10+ 21	−0.002	117.827
R35	CHO(b) + OH(a) ⇄ H2O(a) + CO(b)	2.992∙10+ 22	0.001	2.168	3.113∙10+ 22	−0.001	156.062
R36	CHO(b) + (a) ⇄ HCOO(a) + vac(b)	3.658∙10+ 21	0.0	11.580	1.210∙10+ 21	0.0	8.680
R37	HCOO(a) + OH(a) ⇄ CO2(a) + H2O(a)	2.305∙10+ 23	0.011	193.191	4.912∙10+ 23	−0.011	376.439
R38	HCOO(a) + (b) ⇄ H(b) + CO2(a)	1.681∙10+ 23	0.007	177.623	1.726∙10+ 24	−0.007	368.497
R39	H2O(a) + (b) ⇄ OH(a) + H(b)	3.659∙10+ 21	0.0	12.5	1.763∙10+ 22	0.008	10.126

[25] The unchanged kinetic parameters for the modified Arrhenius expressions are based on DFT derived energetics by Grönbeck et al. [44] with coordinatively unsaturated Pd (a) and lattice oxygen sites of PdO (b) present in the (101) facet and listed subsequently. The detailed reaction simulations are based on mean field approximations comprising the dual sites with a Mars–van Krevelen mechanism. In total, 23 surface intermediates are implemented in the mechanism, 15 species on the related Pd-sites ((a), O(a), O₂(a), OH(a), H₂O(a), CO(a), HCOO(a), H(a), CO₂(a), CH₃(a), CH₂OH(a), CH₂O(a), CHO(a), CH₂(a), CH(a)) and 8 on the oxygen part of the oxide ((b), vac(b), O(b), H(b), CO(b), CH2(b), CH₃(b), CHO(b)). Additionally, these oxide sites can react to form oxygen vacancies (vac(b)) in accordance with the Mars–van-Krevelen formulation. Subsequent regeneration is also considered. CO as an intermediate of the chemical reactions on the surface is not part of the feed gas, thus adsorption and desorption is neglected, leading to an improved numerical performance of the simulations for the remaining participating gas species CH₄, O₂, H₂O, and CO₂. Furthermore, the microkinetic mechanism represents different carbonaceous reaction routes for methane oxidation. A preferential pathway at dry conditions and low temperatures with mainly CH₂OH species over (a) sites is implemented as well as a pathway after light-off at dry conditions and with externally dosed water being present over CH₂ (a) species and a subsequent exchange on (b) sites as described in the reaction pathway analysis [25]. Herein, the new approach to capture the water inhibition effect relies on altering the accessible surface area F_cat,geo for the catalytic reaction, hence thermodynamic consistency is still guaranteed.

3.6. Model Development

Most parts of the simulations were carried out with the software tool CaRMeN (Catalytic reaction mechanism network) [45,46] developed by our group to digitalize the work around catalyst research and reactor modeling. The software provides an efficient way to archive and combine experimental and modeling results, i.e., for light-off experiments as well as spatially resolved simulation along the axial length of a monolith, CaRMeN sufficiently accelerated the process of model development and validation. Based on the present work, the software tool ensured a good visualization of the impact of externally dosed water on the methane conversion during the oxidation process. In addition to the water inhibition effect, the described effect of systematically inaccessible surface area was depictable and comparable instantaneously in order to improve the understanding of the catalytic system.

4. Conclusions

Based on systematic light-off tests in the absence and presence of various steam concentrations, a microkinetic model was extended to capture the instant water deactivation effect of the catalytic methane oxidation over Pd-based catalysts. We introduced a blocking mechanism where the catalytically active surface is covered, thereby decreasing the methane conversion. Based on the trends observed for the activity, which shifts towards a higher temperature with an increasing amount of externally dosed water, we propose that for steam concentrations between 1 and 15% the accessible surface area decreases by 50.0%–87.8%. The model was further tested with profound packed bed and monolith experiments. Additionally, the accuracy was demonstrated by comparing modeled results with experimentally obtained spatially resolved concentration profiles inside a channel of the monolith. This new approach offers a way to include dynamic inhibition effects into microkinetic models of catalytic reactors.