Photocatalytic Hydrogen Production Under Near-UV Using Pd-Doped Mesoporous TiO2 and Ethanol as Organic Scavenger
Abstract
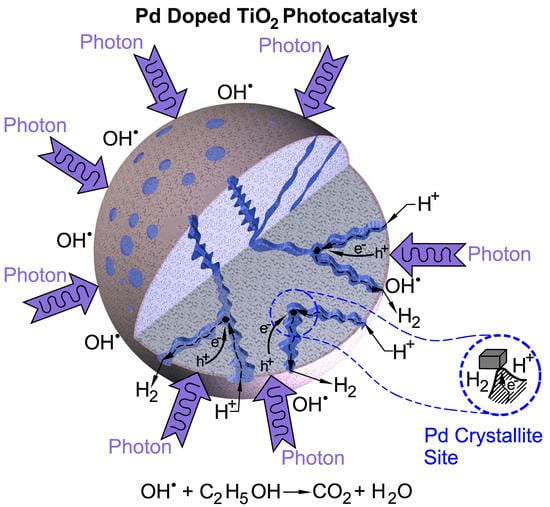
:1. Introduction
2. Results and Discussion
2.1. Photocatalyst Characterization
2.1.1. Brunauer–Emmett–Teller (BET) Surface Area
2.1.2. Pulse Hydrogen Chemisorption
2.1.3. X-Ray Diffraction (XRD)
2.1.4. Band Gap
2.1.5. X-Ray Photoelectron Spectroscopy (XPS)
2.2. Macroscopic Radiation Energy Balance (MREB)
2.3. Hydrogen Production
2.3.1. Effect of Palladium Loadings
2.3.2. Effect of Catalyst Concentration on Hydrogen Production
2.3.3. Effect of Photo-CREC Water II Atmosphere using Argon and CO2
2.3.4. Effect of Sacrificial Agent Concentration
2.3.5. By-Products Formation
2.4. Quantum Yield (QY) evaluation
2.4.1. Effect of Pd Addition on Quantum Yields
2.4.2. Effect of Catalyst Concentration on Quantum Yields
3. Experimental Methods
3.1. Photocatalyst Synthesis
3.2. Equipment
3.3. Photocatalyst Characterization
3.4. Hydrogen Production
3.5. Analytical Techniques
4. Conclusions
- (a)
- The TiO2 mesoporous photocatalysts of the present study were prepared using a F-127 template and following a sol–gel methodology. It was found that the mesoporous prepared using a F-127 template displayed a good photocatalytic performance.
- (b)
- The prepared Pd–TiO2 photocatalysts were characterized using BET, XRD, UV-VIS and XPS. On this basis it was proven that energy band gaps were significantly affected with Pd addition, and that binding energies showed significant contribution of the Pd (0) on the doped-palladium TiO2.
- (c)
- Macroscopic radiation energy balances were successfully employed to establish photon absorption rates and radiation absorption efficiencies in the PCW-II unit. For the Pd–TiO2 semiconductors, photon absorption efficiencies were in the 45 and 60% range under near-UV light.
- (d)
- The formation of hydrogen using Pd–TiO2 photocatalysts followed, in all cases, steady zero-order kinetics with no apparent photocatalyst activity decay.
- (e)
- The prepared Pd–TiO2 photocatalysts under near UV-light were shown to be adequate for hydrogen production reaching up to 210 cm3 STP when using the 1.00 wt%-Pd on TiO2. This photocatalyst showed a best QY% of 30.8%.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| CO2 | Carbon dioxide |
| CH4 | Methane |
| C2H6 | Ethane |
| C2H4O | Acetaldehyde |
| c | Speed of light (3.0 × 108 m/s) |
| Dp | Pore diameter (cm) |
| e- | Electron |
| h+ | Hole |
| h | Planck’s constant (6.63 × 1034 J/s) |
| Ebg | Energy band gap (eV) |
| Eav | Average energy of a photon (kJ/mol photon) |
| F-127 | Poly (ethylene oxide)/poly (propylene oxide)/poly (ethylene oxide) |
| H• | Hydrogen radical |
| H2O | Water |
| I(λ) | Intensity of light (W/cm2) |
| OH- | Hydroxide ions |
| OH• | Hydroxide radicals |
| P-123 | Poly (ethylene glycol)-block-poly (propylene glycol)-block-poly (ethylene glycol) |
| P0 | Rate of photons emitted by the BLB lamp (einstein/s) |
| Pa | Rate of absorbed photons (einstein/s) |
| Pa-wall | Rate of photons absorbed by the inner pyrex glass (einstein/s) |
| Pbs | Rate of backscattered photons exiting the system (einstein/s) |
| Pd | Palladium |
| PdCl2 | Palladium II chloride |
| PEO | Poly (ethylene oxide) |
| Pfs | Rate of forward-scattered radiation (einstein/s) |
| Pi | Rate of photons reaching the reactor inner surface (einstein/s) |
| Pns | Rate of transmitted non-scattered radiation (einstein/s) |
| PPO | Poly (propylene oxide) |
| Pt | Rate of transmitted photons (einstein/s) |
| Pt | Platinum |
| q (θ, z, λ, t) | Net radiative flux over the lamp emission spectrum (μW/cm2) |
| t | Time (h) |
| TiO2 | Titanium dioxide |
| V | Total volume of the gas chamber (5716 cm3) |
| W | Weight (g) |
| Wt% | Weight percent (% m/m) |
| Greek symbols | |
| θ | Diffraction angle, also scattering angular angle (o) |
| λ | Wave length (nm) |
| φ | Quantum Yield Efficiency (%) |
| Acronyms | |
| BJH | Barrett–Joyner–Halenda model |
| BLB | Black light blue lamp |
| BET | Brunauer–Emmett–Teller Surface Area Method |
| CB | Conduction band |
| DP25 | Degussa P25 (TiO2) |
| JCPDS | International Centre for Diffraction Data |
| MIEB | Macroscopic Irradiation Energy Balance |
| PCW-II | Photo CREC Water II reactor |
| PC | Photocatalyst concentration |
| STP | Standard temperature and pressure (273 K and 1 atm) |
| UV | Ultraviolet |
| VB | Valence band |
| Bg | Band gap |
Appendix A. Lamp Characterization


Appendix B. Semiconductor Crystallite Sizes and Lattice Parameters
| Photocatalyst | Crystallite Size (nm) |
|---|---|
| TiO2 | 9 |
| TiO2 0.25 wt% Pd 500 °C | 11 |
| TiO2 0.50 wt% Pd 500 °C | 11 |
| TiO2 1.00 wt% Pd 500 °C | 11 |
| TiO2 2.50 wt% Pd 500 °C | 13 |
| TiO2 5.00 wt% Pd 500 °C | 14 |
| Photocatalyst | a = b | c | 2θ (deg) | d (Å) |
|---|---|---|---|---|
| TiO2 [53] | 3.7821 | 9.5022 | 25.33 | 3.5139 |
| TiO2 500 °C (our study) | 3.7679 | 9.5002 | 25.41 | 3.5025 |
| TiO2 0.25 wt% Pd 500 °C | 3.7832 | 9.4833 | 25.33 | 3.5139 |
| TiO2 0.50 wt% Pd 500 °C | 3.7858 | 9.4737 | 25.31 | 3.5155 |
| TiO2 1.00 wt% Pd 500 °C | 3.7825 | 9.5099 | 25.32 | 3.5147 |
| TiO2 2.50 wt% Pd 500 °C | 3.7748 | 9.4713 | 25.38 | 3.5065 |
| TiO2 5.00 wt% Pd 500 °C | 3.7691 | 9.4809 | 25.41 | 3.5025 |
Appendix C. Quantum Yield Calculation
References
- Ramesohl, S.; Merten, F. Energy system aspects of hydrogen as an alternative fuel in transport. Energy Policy 2006, 34, 1251–1259. [Google Scholar] [CrossRef]
- Barreto, L.; Makihira, A.; Riahi, K. The hydrogen economy in the 21st century: A sustainable development scenario. Int. J. Hydrogen Energy 2003, 28, 267–284. [Google Scholar] [CrossRef]
- Maeda, K.; Teramura, K.; Lu, D.; Takata, T.; Saito, N.; Inoue, Y.; Domen, K. Photocatalyst releasing hydrogen from water. Nature 2006, 440, 295. [Google Scholar] [CrossRef] [PubMed]
- Galińska, A. Photocatalytic Water Splitting over Pt−TiO2 in the Presence of Sacrificial Reagents. Energy Fuels 2005, 19, 1143–1147. [Google Scholar] [CrossRef]
- Wang, M.; Shen, S.; Li, L.; Tang, Z.; Yang, J. Effects of sacrificial reagents on photocatalytic hydrogen evolution over different photocatalysts. J. Mater. Sci. 2017, 52, 5155–5164. [Google Scholar] [CrossRef]
- López, C.R.; Melián, E.P.; Méndez, J.A.O.; Santiago, D.E.; Rodríguez, J.M.D.; Díaz, O.G. Comparative study of alcohols as sacrificial agents in H2production by heterogeneous photocatalysis using Pt/TiO2 catalysts. J. Photochem. Photobiol. A Chem. 2015, 312, 45–54. [Google Scholar] [CrossRef]
- Mills, A. An overview of semiconductor photocatalysis. J. Photochem. Photobiol. A Chem. 1997, 108, 1–35. [Google Scholar] [CrossRef]
- Abe, R. Significant effect of iodide addition on water splitting into H2 and O2 over Pt-loaded TiO2 photocatalyst: Suppression of backward reaction. Chem. Phys. Lett. 2003, 371, 360–364. [Google Scholar] [CrossRef]
- Mills, A. Photosensitised dissociation of water using dispersed suspensions of n-type semiconductors. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1982, 12, 3659–3669. [Google Scholar] [CrossRef]
- Escobedo Salas, S. Photocatalytic Water Splitting Using a Modified Pt-TiO2. Kinetic Modeling and Hydrogen Production Efficiency. Ph.D. Thesis, The University of Western Ontario, London, ON, Canada, August 2013. [Google Scholar]
- Khan, M.M.; Adil, S.F.; Al-Mayouf, A. Metal oxides as photocatalysts. J. Saudi Chem. Soc. 2015, 19, 462–464. [Google Scholar] [CrossRef] [Green Version]
- Haider, A.J. Exploring potential Environmental applications of TiO2 Nanoparticles. Energy Procedia 2017, 119, 332–345. [Google Scholar] [CrossRef]
- Chin, W.L.; Low, F.W.; Chong, S.W.; Hamid, S.B.A. An Overview: Recent Development of Titanium Dioxide Loaded Graphene Nanocomposite Film for Solar Application. Curr. Org. Chem. 2015, 19, 1882–1895. [Google Scholar]
- Yang, J. Roles of Cocatalysts in Photocatalysis and Photoelectrocatalysis. Acc. Chem. Res. 2013, 46, 1900–1909. [Google Scholar] [CrossRef] [Green Version]
- Moslah, C.; Kandyla, M.; Mousdis, G.A.; Petropoulou, G.; Ksibi, M. Photocatalytic Properties of Titanium Dioxide Thin Films Doped with Noble Metals (Ag, Au, Pd, and Pt). Phys. Status Solidi Appl. Mater. Sci. 2018, 215, 1–7. [Google Scholar] [CrossRef]
- García-Zaleta, D.S.; Torres-Huerta, A.M.; Domínguez-Crespo, M.A.; García-Murillo, A.; Silva-Rodrigo, R.; González, R.L. Influence of Phases Content on Pt/TiO2, Pd/TiO2 Catalysts for Degradation of 4-Chlorophenol at Room Temperature. J. Nanomater. 2016, 2016, 1805169. [Google Scholar] [CrossRef]
- Subramanian, V.; Wolf, E.E.; Kamat, P.V. Catalysis with TiO2/Gold Nanocomposites. Effect of Metal Particle Size on the Fermi Level Equilibration. J. Am. Chem. Soc. 2004, 126, 4943–4950. [Google Scholar] [CrossRef]
- Santara, B.; Pal, B.; Giri, P.K. Signature of strong ferromagnetism and optical properties of Co doped TiO2 nanoparticles. J. Appl. Phys. 2011, 110, 114322. [Google Scholar] [CrossRef]
- Khairy, W.; Zakaria, M. Effect of metal-doping of TiO2 nanoparticles on their photocatalytic activities toward removal of organic dyes. Egypt. J. Pet. 2014, 23, 419–426. [Google Scholar] [CrossRef]
- Sobana, N.; Muruganadham, M.; Swaminathan, M. Nano-Ag particles doped TiO2 for efficient photodegradation of Direct azo dyes. J. Mol. Catal. A Chem. 2006, 258, 124–132. [Google Scholar] [CrossRef]
- Cassano, A.E.; Martin, C.A.; Brandi, R.J.; Alfano, O.M. Photoreactor Analysis and Design: Fundamentals and Applications. Ind. Eng. Chem. Res. 1995, 34, 2155–2201. [Google Scholar] [CrossRef]
- Escobedo, S.; Serrano, B.; Calzada, A.; Moreira, J.; de Lasa, H. Hydrogen production using a platinum modified TiO2 photocatalyst and an organic scavenger. Kinetic modeling. Fuel 2016, 181, 438–449. [Google Scholar] [CrossRef]
- Yu, J.C.; Wang, X.; Fu, X. Pore-Wall Chemistry and Photocatalytic Activity of Mesoporous Titania Molecular Sieve Films. Chem. Mater. 2004, 16, 1523–1530. [Google Scholar] [CrossRef]
- Pan, X.; Xu, Y.J. Defect-mediated growth of noble-metal (Ag, Pt, and Pd) nanoparticles on TiO2 with oxygen vacancies for photocatalytic redox reactions under visible light. J. Phys. Chem. C 2013, 117, 17996–18005. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, P.; Liu, J.; Yu, J. New understanding of the difference of photocatalytic activity among anatase, rutile and brookite TiO2. Phys. Chem. Chem. Phys. 2014, 16, 20382–20386. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Vindas, D. Synthesis of palladium with different nanoscale structures by sputtering deposition onto fiber templates. J. Nanophotonics 2008, 2, 021925. [Google Scholar] [CrossRef]
- Moreira, J.; Serrano, B.; Ortiz, A.; de Lasa, H.; de Lasa, H. Evaluation of Photon Absorption in an Aqueous TiO2 Slurry Reactor Using Monte Carlo Simulations and Macroscopic Balance. Ind. Eng. Chem. Res. 2010, 49, 10524–10534. [Google Scholar] [CrossRef]
- Salaices, M.; Serrano, B.; de Lasa, H.I. Experimental evaluation of photon absorption in an aqueous TiO2 slurry reactor. Chem. Eng. J. 2002, 90, 219–229. [Google Scholar] [CrossRef]
- Thornton, J.M.; Raftery, D. Efficient photocatalytic hydrogen production by platinum-loaded carbon-doped cadmium indate nanoparticles. ACS Appl. Mater. Interfaces 2012, 4, 2426–2431. [Google Scholar] [CrossRef]
- Yoshida, H.; Hirao, K.; Nishimoto, J.; Shimura, K.; Kato, S.; Itoh, H.; Hattori, T. Hydrogen production from methane and water on platinum loaded titanium oxide photocatalysts. J. Phys. Chem. C 2008, 112, 5542–5551. [Google Scholar] [CrossRef]
- Rusinque, B. Hydrogen Production by Photocatalytic Water Splitting Under Near-UV and Visible Light Using Doped Pt and Pd TiO2. Master Thesis, The University of Western Ontario, London, ON, Canada, September 2018. [Google Scholar]
- Zhang, N.; Liu, S.; Fu, X.; Xu, Y.J. Synthesis of M@TiO2 (M = Au, Pd, Pt) core-shell nanocomposites with tunable photoreactivity. J. Phys. Chem. C 2011, 115, 9136–9145. [Google Scholar] [CrossRef]
- Riyapan, S.; Boonyongmaneerat, Y.; Mekasuwandumrong, O.; Yoshida, H.; Fujita, S.; Arai, M.; Panpranot, J. Improved catalytic performance of Pd/TiO2in the selective hydrogenation of acetylene by using H2-treated sol-gel TiO2. J. Mol. Catal. A Chem. 2014, 383–384, 182–187. [Google Scholar] [CrossRef]
- Akbayrak, S.; Tonbul, Y.; Özkar, S. Nanoceria supported palladium(0) nanoparticles: Superb catalyst in dehydrogenation of formic acid at room temperature. Appl. Catal. B Environ. 2017, 206, 384–392. [Google Scholar] [CrossRef]
- Borodin, V.B.; Tsygankov, A.A.; Rao, K.K.; Hall, D.O. Hydrogen production byAnabaena variabilisPK84 under simulated outdoor conditions. Biotechnol. Bioeng. 2000, 69, 478–485. [Google Scholar] [CrossRef]
- Dalmolin, I.; Skovroinski, E.; Biasi, A.; Corazza, M.L.; Dariva, C.; Oliveira, J.V. Solubility of carbon dioxide in binary and ternary mixtures with ethanol and water. Fluid Phase Equilib. 2006, 245, 193–200. [Google Scholar] [CrossRef]
- Puangpetch, T.; Sreethawong, T.; Yoshikawa, S.; Chavadej, S. Hydrogen production from photocatalytic water splitting over mesoporous-assembled SrTiO3nanocrystal-based photocatalysts. J. Mol. Catal. A Chem. 2009, 312, 97–106. [Google Scholar] [CrossRef]
- Ibrahim, H.; de Lasa, H. Novel photocatalytic reactor for the destruction of airborne pollutants reaction kinetics and quantum yields. Ind. Eng. Chem. Res. 1999, 38, 3211–3217. [Google Scholar] [CrossRef]
- Escobedo, S.; Serrano, B.; de Lasa, H. Serrano and H. de Lasa. Quantum Yield with Platinum Modified TiO2 Photocatalysts for Hydrogen Prodcution. Appl. Catal. B. Environ. 2013, 140, 523–536. [Google Scholar] [CrossRef]
- Guo, S.P.; Li, J.C.; Xu, Q.T.; Ma, Z.; Xue, H.G. Recent achievements on polyanion-type compounds for sodium-ion batteries: Syntheses, crystal chemistry and electrochemical performance. J. Power Sources 2017, 361, 285–299. [Google Scholar] [CrossRef]
- Brinker, J.; Schere, G.W. Sol-Gel Science: The Physics and Chemistry of Sol-Gel Processing; Academic Press Inc.: San Diego, CA, USA, 1990. [Google Scholar]
- He, X. Recent Progress in Fabrication of Nanostructured Carbon Monolithic Materials; Elsevier: Oxford, UK, 2017. [Google Scholar]
- Guayaquil-Sosa, J.F.; Serrano-Rosales, B.; Valadés-Pelayo, P.J.; de Lasa, H. Photocatalytic hydrogen production using mesoporous TiO2 doped with Pt. Appl. Catal. B Environ. 2017, 211, 337–348. [Google Scholar] [CrossRef]
- De Lasa, H.; Serrano, B.; Salaices, M. Photocatalytic Reaction Engineering; Springer Scicence: New York, NY, USA, 2005. [Google Scholar]
- Ushio. UV-B Blacklight & Blacklight Blue; Catalogue: Cypress, CA, USA.
- AutoChem 2920 Automated Catalyst Characterization System Operator’s Manual; AutoChem: Norcross, GA, USA, 2014.
- Warren, B.E. X-Ray Diffraction; Dover Publications: New York, NY, USA, 1990. [Google Scholar]
- UV-VIS-NIR Spectrophotometer; Shimadzu: Tokyo, Japan, 2018.
- Slav, A. Optical characterization of TiO2 -Ge nanocomposite films obtained by reactive magnetron sputtering. Dig. J. Nanomater. Biostructures 2011, 6, 915–920. [Google Scholar]
- Briggs, D. X: X-Ray Photoelectron Spectroscopy. In Handbook of Adhesion, 2nd ed.; 2005; pp. 621–622. [Google Scholar]
- Serrano, B.; Ortíz, A.; Moreira, J.; de Lasa, H.I. Energy efficiency in photocatalytic reactors for the full span of reaction times. Ind. Eng. Chem. Res. 2009, 48, 9864–9876. [Google Scholar] [CrossRef]
- Salaices, M.; Serrano, B.; De Lasa, H. Photocatalytic conversion of Organic pollutants extinction coefficients and quantum effiencies. Ind. Eng. Chem. Res. 2001, 40, 5455–5464. [Google Scholar] [CrossRef]
- Treacy, J.P.W.; Hussain, H.; Torrelles, X.; Grinter, D.C.; Cabailh, G.; Bikondoa, O.; Nicklin, C.; Selcuk, S.; Selloni, A.; Lindsay, R.; et al. Geometric structure of anatase Ti O2(101). Phys. Rev. B 2017, 95, 1–7. [Google Scholar] [CrossRef]















| Photocatalyst | SBET (m2 g−1) | DpBJH (4VpBJH/SBET) (nm) | VpBJH (cm3g−1) |
|---|---|---|---|
| Degussa P-25 | 59 | 7.5 | 0.25 |
| F-127–TiO2 500 °C | 140 | 17.5 | 0.61 |
| Photocatalyst | SBET (m2 g−1) | Dp BJH (4VpBJH/SBET) (nm) | VpBJH (cm3g−1) |
|---|---|---|---|
| Anatase | 11 | 7.3 | 0.05 |
| Rutile | 5 | 4.7 | 0.05 |
| Degussa P-25 | 59 | 7.5 | 0.25 |
| F-127–TiO2-500 °C | 140 | 17.5 | 0.61 |
| F-127–0.25 wt% Pd–TiO2 500 °C | 131 | 16.5 | 0.53 |
| F-127–0.50 wt% Pd–TiO2 500 °C | 124 | 16.8 | 0.52 |
| F-127–1.0 wt% Pd–TiO2 500 °C | 123 | 21.2 | 0.65 |
| F-127–2.5 wt% Pd–TiO2 500 °C | 122 | 19.9 | 0.60 |
| F-127–5.0 wt% Pd–TiO2 500 °C | 119 | 18.9 | 0.56 |
| Photocatalyst | Metal Dispersion (%) |
|---|---|
| F-127–0.25 wt% Pd–TiO2 500 °C | 75 |
| F-127–0.50 wt% Pd–TiO2 500 °C | 27 |
| F-127–1.0 wt% Pd–TiO2 500 °C | 26 |
| F-127–2.5 wt% Pd–TiO2 500 °C | 12 |
| F-127–5.0 wt% Pd–TiO2 500 °C | 8 |
| Near-UV Light | Pa (Einstein/s) |
|---|---|
| TiO2 | 3.11 × 106 |
| 0.25 wt% Pd | 3.18 × 10−6 |
| 0.50 wt% Pd | 3.52 × 10−6 |
| 1.00 wt% Pd | 5.11 × 10−6 |
| 2.50 wt% Pd | 3.77 × 10−6 |
| 5.00 wt% Pd | 3.76 × 10−6 |
| Semiconductor | QY (%) |
|---|---|
| F–127 TiO2 | 5.0 |
| F-127–0.25 wt% Pd–TiO2 | 13.7 |
| F-127–0.50 wt% Pd–TiO2 | 12.8 |
| F-127–1.00 wt% Pd–TiO2 | 10.9 |
| F-127–2.50 wt% Pd–TiO2 | 9.6 |
| F-127–5.00 wt% Pd–TiO2 | 8.5 |
| Catalyst Concentration (g/L) | QY (%) |
|---|---|
| 0.15 | 10.9 |
| 0.30 | 14.5 |
| 0.50 | 22.4 |
| 1.00 | 30.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rusinque, B.; Escobedo, S.; Lasa, H.d. Photocatalytic Hydrogen Production Under Near-UV Using Pd-Doped Mesoporous TiO2 and Ethanol as Organic Scavenger. Catalysts 2019, 9, 33. https://doi.org/10.3390/catal9010033
Rusinque B, Escobedo S, Lasa Hd. Photocatalytic Hydrogen Production Under Near-UV Using Pd-Doped Mesoporous TiO2 and Ethanol as Organic Scavenger. Catalysts. 2019; 9(1):33. https://doi.org/10.3390/catal9010033
Chicago/Turabian StyleRusinque, Bianca, Salvador Escobedo, and Hugo de Lasa. 2019. "Photocatalytic Hydrogen Production Under Near-UV Using Pd-Doped Mesoporous TiO2 and Ethanol as Organic Scavenger" Catalysts 9, no. 1: 33. https://doi.org/10.3390/catal9010033
APA StyleRusinque, B., Escobedo, S., & Lasa, H. d. (2019). Photocatalytic Hydrogen Production Under Near-UV Using Pd-Doped Mesoporous TiO2 and Ethanol as Organic Scavenger. Catalysts, 9(1), 33. https://doi.org/10.3390/catal9010033