Next Article in Journal
Effect of Structure-Controlled Ruthenium Oxide by Nanocasting in Electrocatalytic Oxygen and Chlorine Evolution Reactions in Acidic Conditions
Next Article in Special Issue
Carbon Deposition Behavior of Ni Catalyst Prepared by Combustion Method in Slurry Methanation Reaction
Previous Article in Journal
Developing Multicompartment Biopolymer Hydrogel Beads for Tandem Chemoenzymatic One-Pot Process
Previous Article in Special Issue
Lignin Valorizations with Ni Catalysts for Renewable Chemicals and Fuels Productions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Catalysts
Volume 9
Issue 6
10.3390/catal9060548
catalysts-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Computational Investigation of Nickel-Mediated B–H Activation and Regioselective Cage B–C(sp2) Coupling of o-Carborane

by
Wei-Hua Mu
1,*,
Wen-Zhu Liu
1,
Rui-Jiao Cheng
1,
Li-Juan Dou
1,
Pin Liu
1 and
Qiang Hao
2,*
1
Faculty of Chemistry and Chemical Engineering, Yunnan Normal University, Kunming 650092, China
2
School of Chemistry and Chemical Engineering, Liaoning Normal University, Dalian 116029, China
*
Authors to whom correspondence should be addressed.
Catalysts 2019, 9(6), 548; https://doi.org/10.3390/catal9060548
Submission received: 30 April 2019 / Revised: 12 June 2019 / Accepted: 14 June 2019 / Published: 18 June 2019
(This article belongs to the Special Issue Ni-Containing Catalysts)
Browse Figures
Review Reports Versions Notes

Abstract

:
Density functional theory (DFT) methods including LC-ωPBE, CAM-B3LYP, B3LYP, and B3LYP-D3, combined with double Zeta all-electron DZVP basis set, have been employed to conduct computational investigations on nickel-mediated reaction of o-carboranylzirconacycle, n-hexene, and 2-bromophenyltrimethylsilylacetylene in toluene solution. A multistep mechanism leading to the C,C,B-substituted carborane-fused tricyclics, including (1) sequential insertion of alkene and alkyne into Ni–C bonds; (2) double 1,2-migration of the TMS group; (3) B–H activation assisted by Cs2CO3 additive; and (4) reduction cage B–C (sp2) coupling, was proposed. Among these steps, the B–H activation of o-carborane was located as rate-determining step (RDS). With assistance of Cs2CO3 additive (replaced by K2CO3 in simulation), the RDS free-energy barrier at PCM-LC-ωPBE/DZVP level was calculated to be 23.1–23.9 kcal·mol−1, transferring to a half-life of 3.9–15.1 h at 298 K. The predicted half-life coincides well with 80% experimental yields of C,C,B-substituted carborane-fused tricyclics after 12 h. Kinetic data obtained by employing LC-ωPBE method also reproduced the experimental diastereoselective ratio well. Various B–H activation pathways with and without Cs2CO3 additive were taken into consideration, which illustrates Cs2CO3 as an essential guarantee for smooth occurrence of this reaction at room temperature.

Graphical Abstract

1. Introduction

Icosahedral o-carborane is a class of boron hydride clusters, in which two adjacent B–H vertices are replaced by C–H units, and has potential applications in boron neutron capture therapy (BNCT), organic synthetic, cancer treatment, drug development, and supramolecular design [1,2,3,4,5,6,7]. Due to its unique electronic properties and geometrical structure, the icosahedral o-carborane possesses unusual reactivity and can be activated by transition metal through C–H or B–H activation, to form a wide variety of o-carborane derivatives [8,9,10,11,12,13]. Remarkable achievements, in terms of substrate expansion, optimization of experimental conditions, and product yield enhancement, have been made in C–H activation and functionalization of o-carborane in recent years [8,9,14,15,16]. Based on computational simulations, some scholars have even presented reasonable explanations for reaction mechanisms and regioselectivity of C–H activation in o-carborane [17,18,19,20,21,22,23], which has also promoted the rapid development of this area.
However, owing to simultaneous existence of multiple B–H bonds with varying chemical environment, the regioselective activation of B–H bond in o-carborane remains a challenging topic and has always been a focus in the field [10,11,12,13]. In recent decades, people have made significant achievements in nickel-catalyzed selective activation of B–H bonds in o-carborane, generally by introducing a directing group in substrates. For example, in 2010, Qiu and Xie had realized the palladium/nickel co-mediated [2+2+2] cyclization of 1-lithium-2-methyl-3-iodo-o-carborane with twice equivalent of alkynes, and prepared 1-C-3-B-substituted o-carborane derivative successfully [24]. This reaction has not only excellent yield but also good regioselectivity. In 2014, Xie’s group had achieved three-component cyclization of o-carborane with olefin and halogenated phenyl alkyne through zirconium/nickel co-mediated coupling, and prepared a series of novel C,C,B-substituted carborane-fused tricyclics successfully (Scheme 1) [25]. This work represents the first example of cage B–C(sp2) coupling by direct B–H activation of o-carborane, which is of great significance for the regioselective B–H activation and functionalization of o-carborane derivatives. What particularly worth mentioning is, the reaction can process at room temperature and corresponding C,C,B-substituted carborane-fused tricyclics (P1) can be obtained with a yield up to 80% by adding Cs2CO3 additive (Entry 2 in Scheme 1).
Pioneered by previous reports [20,26], authors speculated that the reaction of o-carboranylzirconacycle (R1), n-hexene (R2) and 2-bromophenyltrimethylsilylacetylene (R3), as shown in Scheme 1, might go through the nickelacyclopentane intermediate M1, dihydrofulvenocarborane intermediates M2 and M3, the nickelacycloheptene intermediates M4 (or M4’) sequentially, and form the C,C,B-substituted o-carborane-fused tricyclic derivative P1a/b in the end. However, due to the limitation of experimental means in detecting unstable and reactive intermediates, the aforementioned mechanism is still under proposal. On the other hand, affected by many factors such as large size of o-carboranyl group, many electrons involved in transition metals, and diverse regioselectivities of o-carborane’s B–H activation, it is really challenging in computational cost to conduct theoretical studies on transition metal catalyzed regioselective B–H activation of o-carborane. Our group has recently conducted a computational study on palladium-catalyzed regioselective B–H activation and diarylation of o-carboranes with aryl iodides in solution, and found that the substituents on o-carborane have a significant effect on the regioselectivity of B–H activation [27]. In contrast to this, the presence of a fused five-membered ring in intermediates M2 and M3 (Scheme 1) here would affect the regioselectivity of B–H activation significantly, and lead to different diastereoselectivities in the following cage B–C(sp2) coupling through direct B–H activation of o-carborane. Unfortunately, it is hard to confirm the validity of this speculation based on existing literature. Therefore, further theoretical research is required for better understanding of the reaction shown in Scheme 1.
To clarify the microscopic mechanism and rationalize experimentally detected diastereoselectivities of reaction shown in Scheme 1, density functional methods of LC-ωPBE, CAM-B3LYP, B3LYP, and B3LYP-D3, combining with the double-ζ all-electron DZVP basis set, were employed to conduct computational study on nickel-mediated B–H activation of o-carboranylzirconacycle with n-hexene and 2-bromophenyltrimethylsilylacetylene in toluene solution (Entry 2). For more accurate simulation, the experimentally operated reaction with none substituents truncated or simplified, was taken into consideration. The mechanism, diastereoselectivity of B–H activation, and role of Cs2CO3 additive will be explored and discussed in detail in the following parts.

2. Computational Details

All calculations reported here were performed with Gaussian 09 program [28], using an ultrafine integration grid of (99,590). LC-ωPBE [29,30], CAM-B3LYP [31], B3LYP [32,33] and B3LYP-D3 [34,35] density functional methods, as well as the double-ζ valence polarized (DZVP) [36,37] and triple-ζ valence polarized (TZVP) basis sets [38,39] employed in this paper were all set by default in Gaussian 09 program. All stationary points reported were confirmed by harmonic vibrational analyses based on geometrical optimizations employing DZVP basis set, in which all minima feature no imaginary frequency and all transition states feature only one imaginary frequency corresponding to correct reaction directions. To ensure that every transition state is connected to specific reactants, products or intermediates, intrinsic reaction coordinate (IRC) [40,41,42] track on key transition states were performed.
For better simulation of the reaction, experimentally performed toluene (ε = 2.37) solvent effect were taken into consideration in both optimization and single-point calculation tasks, by employing a self-consistent reaction field (SCRF) polarization continuum model (PCM) [43,44] and isodensity-based SCRF radii (denoted IDSCRF) [45]. Unless noticed elsewhere, all Gibbs free energies reported in this article were obtained based on solution geometrical optimization in toluene, and corrected at experimental temperature (298 K) by using THERMO program [46]. During the revision of this manuscript, single-point calculations on stationary points at PCM-METHOD/TZVP//DZVP level (METHOD = LC-ωPBE, CAM-B3LYP, B3LYP, and B3LYP-D3 respectively) were performed wherever necessary. Considering both potassium and cesium elements belong to the same main group in periodic table and have similar electronic and chemical properties, we employed K2CO3 in place of Cs2CO3 in our simulations for convenience. Natural Bond Orbital (NBO) [47,48,49] analysis, as implemented in Gaussian 09 program, was also performed on selected stationary points to investigate their atomic charge population.

3. Results and Discussion

3.1. Mechanism

3.1.1. Formation Mechanism of Dihydrofulvenocarborane Intermediate INT8

We have firstly conducted calculations on the NiCl2(PMe3)2-mediated reaction of o-carboranylzirconacycle (R1), n-hexene (R2) and 2-bromophenyltrimethylsilylacetylene (R3) at PCM-LC-ωPBE/DZVP level in toluene solution, with results presented in Scheme 2, Figure 1 and Figure 2. According to previous reports [17], alkene insertion into the Ni–C bond is preferred over alkyne insertion when the Ni-carboranyl compound undergoes cycloaddition with alkene and alkyne. Also, in the presence of NiCl2(PMe3)2, o-carboranylzirconacycle R1 would interact with alkene R2 and the catalyst to form a nickelacyclopentane intermediate M1 by transmetallation [16,20,26], then M1 complexes with alkyne to form a new compound INT1 (Scheme 2). However, affected by variable orientation of nBu group in intermediate M1 and subsequent B–H activation sites of o-carborane, the reaction shown in Scheme 1 led to a diastereoselective mixture of P1a and P1b (dr ≈ 1:1) [25]. The later process of this reaction is totally different from the [2+2+1] cycloaddition of o-carborane with alkene and non-halogenated phenyl alkyne, in which none B–H activation occurred [26]. Based on PCM-LC-ωPBE/DZVP level’s optimization in toluene solution, the formation of intermediate M1 from R1, R2 and the nickel catalyst is an exothermic process, releasing 26.0 kcal·mol−1 of Gibbs free energies in total (See Figure S1 in the Supplementary File). For convenience, M1+R3 is selected as the starting point of entire potential energy surfaces (PESs), and all discussion about reaction mechanism, diastereoselectivity, and the role of Cs2CO3 additive here were based on uniform orientation of nBu group in INT1.
Owing to complexation between intermediate M1 and alkyne R3, the bond lengths of Ni(3)–C(2), Ni(3)–C(4) and Ni(3)–P in INT1 are calculated to be 1.93, 1.92 and 2.35 Å respectively, about 0.09, 0.06 and 0.08 Å lengthened when compared to their counterparts in M1 (Figure 2). Meanwhile, the C(6)–C(7) bond in INT1 is located at 1.24 Å, about 0.03 Å lengthened when compared to that in 2-bromophenyltrimethylsilylacetylene (R3). Both of this indicate that there is indeed some complexation interaction between 2-bromophenyltrimethylsilylacetylene (R3) and the nickel center in INT1. When C(6) atom in INT1 gets nearer to C(4), alkyne R3 would realize its insertion into the Ni-C bond through transition state TS1. As shown in Figure 1, the transformation from INT1 to INT2 through TS1 needs to get over a free-energy barrier of 5.9 kcal·mol−1 at PCM-LC-ωPBE/DZVP level. Considering INT1’s formation from M1+R3 is exothermic of 4.7 kcal·mol−1 free energies, the transformation of M1+R3 into INT2 should be very fast at an experimental temperature of 298 K. In TS1, the bond length of C(4)–C(6) is located at 2.16 Å. Due to the insertion of 2-bromophenyltrimethylsilylacetylene (R3), the bond length of Ni(3)–C(4) increased from 1.92 Å (in INT1) to 1.96 Å (in TS1), and C(6)–C(7) bond is lengthened to 1.29 Å (Figure 2), showing a tendency to become a C=C double bond.
Intermediate INT2 formed from INT1 through transition state TS1 is exothermic of 11.1 kcal·mol−1 in energy, and can isomerize to another intermediate INT3 by getting over a free-energy barrier of 14.4 kcal·mol−1 (TS2 in Figure 1). In INT3, the bond length of Ni–C(6) is shortened from 2.19 Å (in INT2) to 1.94 Å (Figure 2), indicating that intermediate INT3 has the characteristics of an alkenyl nickel complex. Then, with assistance of the nickel center, TMS group in INT3 will migrate from C(6) to C(7) through double 1,2-migration, as demonstrated in Scheme 2. The Gibbs free-energy barriers corresponding to the migration processes are 10.5 (TS3) and 2.4 kcal·mol−1 (TS4) respectively, which can be easily overcome at corresponding experimental temperature (298 K). Since intermediate INT4 formed through the first 1,2-migration of TMS group is relatively unstable (Figure 1), it will be rapidly converted into a more stable nickelahexane intermediate INT5. In INT5, the bond lengths of Ni–C(2) and Ni–C(6) are 1.89 and 1.76 Å, respectively (Figure 2), indicates effective coordination between Ni atom and C(2)/C(6) atoms.
Thereafter, to promote the B–H activation and subsequent cage B–C(sp2) coupling of o-carborane, as well as effectively reduce the steric hindrance between TMS and PMe3 groups, intermediate INT5 will convert to intermediate INT6 through transition state TS5. The Gibbs free-energy barrier corresponding to TS5 is 14.6 kcal·mol−1, about 0.2 and 4.1 kcal·mol−1 higher than TS2 and TS3, respectively (Figure 1). It is deemed that the stabilization from the catalytic center has played an essential role in facilitating this dihedral flip process [20] and ensured its easy occurrence at room temperature. After the formation of intermediate INT6, it would undergo reduction elimination via transition state TS6 and convert itself to a carboranylcyclopentane derivative INT7, which requires to get across a free-energy barrier of 17.9 kcal·mol−1. Although the free-energy barrier corresponding to TS6 is 3.3 kcal·mol−1 higher than TS5 (Figure 1), it can still be easily overcome at an experimental temperature of 298 K.
As shown in Figure 1 and Scheme 2, the nickel center (NiPMe3) in complex INT7 can easily realize its insertion into the phenyl C(sp2)–Br bond through transition state TS7, and convert itself to a more stable intermediate INT8 meanwhile. Successful location of INT8 verifies the rationality of experimentally proposed existence of intermediate M3 in Scheme 1. This process only needs to overcome a free-energy barrier of 4.6 kcal·mol−1. On contrary, the leaving of NiPMe3 fragment needs to absorb 20.4 kcal·mol−1 free energies (Figure S3), which indicates the speculated intermediate M2 in Scheme 1 seems not on the optimal pathway. In transition state TS7, the bond length of C(9)–Br is extended from 1.91 Å (in INT7) to 1.92 Å, showing small tendency of stretch and breaking (Figure 2). The bond lengths of C(9)–Ni and Br–Ni bonds in intermediate INT8 are calculated to be 1.87 and 2.38 Å respectively, indicates that the nickel center has inserted into the C(9)–Br bond completely. The formation of intermediate INT8 lays an essential foundation for subsequent B–H activation of o-carborane and final generation of the C,C,B-substituted o-carborane-fused tricyclic product P1a/b.
Hoping for more accurate energy results, we have further conducted single-point calculation by employing a larger TZVP basis set based on the DZVP optimized geometries. As what presented in parentheses in Figure 1, only tiny deviation of TZVP free-energy results from DZVP ones can be observed, similar to what found out by Řezáč and co-authors [50].

3.1.2. Mechanism of B–H Activation and Cage B–C(sp2) Coupling of o-Carborane

To investigate the B–H activation and cage B–C (sp2) coupling mechanism of o-carborane, we then conducted calculations on the B(11)–H activation of intermediate INT8 at PCM-LC-ωPBE/DZVP level in toluene solution, with corresponding results summarized in Figure 3 and Figure 4. The diastereoselective formation of P1b through B(17)–H activation will be discussed in part 3.3 in the following.
As shown in Figure 3, when Cs2CO3 (replaced by K2CO3 firstly, See Figure S4 and line 373–386 for details) is available in the reaction, intermediate INT8 will be converted to complex COM1a through activation of the spatially most favorable B(11)–H (TS8a). The free-energy barrier corresponding to TS8a is calculated to be 23.1 kcal·mol−1 at PCM-LC-ωPBE/DZVP level, which is 5.2 kcal·mol−1 higher than that of TS6 (17.9 kcal·mol−1, represents the highest barrier before TS8a). The reaction rate constant converted from free-energy barrier of TS8a is 7.113 × 10−5 L·mol−1·s−1, which is significantly smaller than any of that transferred from free-energy barriers of TS1–TS7 (Table S1). Taking the whole PESs (Figure 1 and Figure 3) into consideration, the B(11)–H activation process of intermediate INT8 (via TS8a) features the highest barrier (23.1 kcal·mol−1), which indicates significant limit of TS8a on the overall reaction rate, and is therefore the rate-determining step (RDS) of entire reaction.
In transition state TS8a, the activation of B(11)–H and synchronous formation of Ni-B(11) bond is realized under the help of K2CO3 additive, through an interaction between one oxygen atom in CO32− ion and the migrated H(12) atom (Figure 4). The bond lengths of B(11)–H(12), H(12)–O(13), Ni–B(11) and Ni–Br bonds in TS8a are calculated to be 1.46, 1.40, 2.09 and 2.46 Å respectively, in accordance with subsequent formation of KHCO3 and KBr fragments. As depicted in Figure 3, complex COM1a would drop KHCO3 and KBr fragments and transform itself into intermediate INT9a, being endothermic of 13.1 kcal·mol−1 of free energies.
Finally, the direct cage B–C(sp2) coupling in intermediate INT9a is achieved through coupling of B(11) and C(9) in transition state TS9a, and the C,C,B-substituted carborane-fused product P1a is formed through reduction elimination, accompanied by regeneration of the Ni(PMe3)2 catalyst (CAT). As shown in Figure 3, the conversion of COM1a to P1a via INT9a and TS9a requires overcoming a free-energy barrier of 14.2 kcal·mol−1 (TS9a) in total, which should be smooth under experimental temperature of 298 K. The bond length of C(9)–B(11) in the final product P1a is shortened from 2.07 Å (in TS9a) to 1.57 Å, suggests B(11) on o-carboranyl group has successfully coupled with C(9) on the phenyl group (Figure 4).

3.2. The Role of Cs2CO3 Additive

As a commonly used basic additive, Cs2CO3 is widely used in various reactions [51,52,53,54,55]. To investigate detailed interaction mechanism of Cs2CO3 with intermediate INT8 in this reaction, we have explored another two paths (Path a1 and a2, Figure 5) at the same computational level.
In the absence of Cs2CO3 additive (replaced by K2CO3 in simulation, Path a1), the B(11)–H bond on o-carboranyl group in intermediate INT8 can only be activated under the help of –Br group. As shown in Figure 5, the C,C,B-substituted carborane-fused tricyclic product P1a is formed concurrently with removal of one HBr molecule and regeneration of CAT. The free-energy barrier corresponding to TS8a1 on Path a1 is calculated to be 36.9 kcal·mol−1, about 13.8 kcal·mol−1 higher than that of TS8a on Path a. These results indicate that the Cs2CO3 additive does play an essential role in the activation of B(11)–H bond of INT8, and explains why the reaction needs to be carried out at a higher temperature (383 K) in the absence of Cs2CO3 additive (Entry 1 in Scheme 1). For the case in which K2CO3 is present but only help to stabilize the leaving HBr fragment through its positive charge center (K atom, Path a2 in Figure 5), the free-energy barrier corresponding to transition state TS8a2 is still as high as 30.1 kcal·mol−1, about 7.0 kcal·mol−1 higher than that of TS8a. Other B(11)–H activation pathways of intermediate INT8, such as B(11)–H activation and C(9)–B(11) coupling occur synchronically, as well as the radical pathway employing unrestricted Kohn-Sham function [56] (Path a3 and a4 in Figure S5), have also been tested. The free-energy barrier corresponding to transition state TS8a3 is 29.0 kcal·mol−1, about 5.9 kcal·mol−1 higher than that of TS8a, indicates little competitiveness of Path a3 to Path a under given experimental condition. Dissociation of aryl radical INT8’ from INT8 is endothermic of 39.4 kcal·mol−1 of free energies, which also suggests no necessity for further consideration of Path a4. Based on above computational results, Path a, in which K2CO3 directly participates in the B–H activation of o-carboranyl group in intermediate INT8, is optimal among all five paths. The K2CO3 additive significantly reduces the relative energy and barrier of TS8a, by stabilizing its geometrical structure through direct participation in B(11)–H’s activation, and thus guarantees this reaction’s smooth occurrence at room temperature.
For further confirmation of the rationality of Path a’s dominance in generating P1a, NBO charge population analysis on intermediate INT8 and K2CO3 additive at PCM-LC-ωPBE/DZVP//DZVP level were performed, with corresponding results depicted in Table 1. In intermediate INT8, Br(10) and H(12) atoms are distributed with −0.480 negative charge and +0.041 positive charge respectively; while in K2CO3, O(13) and K(16) atoms are distributed with −1.055 negative charge and +0.932 positive charge, respectively. Therefore, When INT8 interacts with K2CO3, the Br(10) atom with more negative charge populated is prone to interact with K(16) atom, while the H(12) atom with partial positive charge distributed prefers migrating to O(13) atom. Eventually, the KHCO3 and KBr fragments are formed and drop. These NBO charge population results reproduce aforementioned energetic results well, and confirms Path a’s dominance in generating C,C,B-substituted carborane-fused tricyclics P1a.

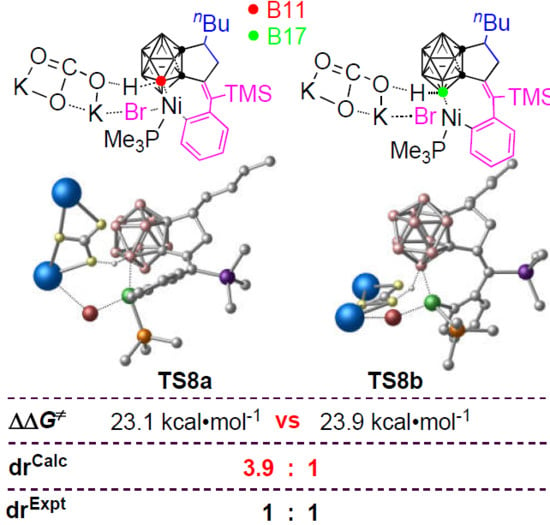
3.3. Diastereoselectivity of B–H Activation of o-Carborane

Many experiments show diverse site-selectivities of B–H activation in different o-carborane-involved reactions [13,25,57], but few of these had been rationalized by computational explorations. According to Quan’s experiments [25], only B(11)–H and B(17)–H (Figure 6) could be activated and corresponding P1a/b (dr ≈ 1:1) products can be detected experimentally (Scheme 1), while B(19)–H or B(20)–H activation products can be obtained in other similar o-carborane-involved reactions [57]. The authors speculated that the specific diastereoselectivity in this reaction was due to coexistence of o-carborane cage and the fused five-membered ring in intermediate INT8, which hindered free rotation of the phenyl group [25].
Based on computational optimization and careful check for the geometry of intermediate INT8, we found the presence of the fused five-membered ring in INT8 greatly limits the reachable range of groups on C(7) atom (Figure 2 and Figure 6), and thus keeps -Br group on the phenyl ring far away from B(19)–H and B(20)–H on o-carboranyl group. In other words, the rigidity of o-carborane cage and the fused five-membered ring in INT8 greatly hinders -Br group on the phenyl ring from getting near to other B–Hs (such as B(19)–H and B(20)–H) except for B(11)–H and B(17)–H on o-carboranyl group. Therefore, B(19)–H and B(20)–H could not be activated, only C,C,B-substituted products P1a/b (dr ≈ 1:1) generated through B(11)/B(17)–H activation can be detected in corresponding experiments.
To investigate the diastereoselectivity of B–H activation in this reaction, calculations at PCM-LC-ωPBE/DZVP level were performed on Path b, with corresponding energy and geometrical results presented in Figure 6 and Figure S6, respectively. Similar to Path a, transition state TS8b on Path b, which corresponds to B(17)–H activation in INT8, is also located as the RDS of entire reaction. The free-energy barrier corresponding to TS8b is calculated to be 23.9 kcal·mol−1. A 0.8 kcal·mol−1 higher free-energy barrier of TS8b than TS8a converts to a diastereoselective ratio (dr, P1a:P1b) of about 3.9:1 (Table 2), coincides well with corresponding experimental dr value (~1:1).
Aiming at better prediction of experimental diastereoselectivities, we employed three different methods (CAM-B3LYP, B3LYP, and B3LYP-D3) and recomputed the optimal Path a and b (as shown in Figure 3 and Figure 6). All stationary points on the PESs were re-optimized and characterized under the same condition but using different density functionals. The free-energy results and corresponding kinetic parameters obtained at PCM-LC-ωPBE/DZVP (denoted LC-ωPBE), PCM-CAM-B3LYP/DZVP (denoted CAM-B3LYP), PCM-B3LYP/DZVP (denoted B3LYP) and PCM-B3LYP-D3/DZVP (denoted B3LYP-D3) levels were summarized in Table 2, with complete potential energy profiles presented in Figure S7 and relative Gibbs free energies summarized in Table S2.
As shown in Table 2, the RDS predicted by B3LYP and CAM-B3LYP methods are the same as what predicted by LC-ωPBE method, which correspond to the activation of B(11)–H through TS8a or activation of B(17)–H through TS8b respectively. Gibbs free-energy barriers of the RDS (TS8a/b) predicted by LC-ωPBE, CAM-B3LYP, and B3LYP methods are calculated to be 23.1/23.9, 24.8/26.9 and 26.7/29.6 kcal·mol−1 respectively; however, when D3 dispersion option was taken into consideration in B3LYP method (denoted B3LYP-D3), the free-energy barriers of TS8a/b are significantly reduced and get much lower than those predicted by LC-ωPBE, CAM-B3LYP and B3LYP methods (14.3–15.2 vs. 23.1–29.6 kcal·mol−1, Table 2). The dramatic decrease of TS8a/b’s barriers, probably arisen from overweight of the weak interaction [58,59] between KHCO3, KBr and other fragments in TS8a/b, makes the next reduction elimination step (INT9a/b → TS9a/b → P1a/b) become RDS of the whole reaction.
The reaction rate constants and half-lives predicted by CAM-B3LYP and B3LYP methods show 1–5 orders of magnitude deviation form corresponding experimental time and yield (80% after 12 hours, Scheme 1). Taking the gold standard of current computational methods (1.0 kcal·mol−1) [60] into consideration, these free-energy barriers obtained by employing CAM-B3LYP and B3LYP methods are reasonable but relatively higher. Satisfactorily, the reaction rate constants and half-lives predicted by LC-ωPBE and B3LYP-D3 methods show only 0–1 orders of magnitude deviation from experimental data, more accurate and reasonable when compared to experimental results. Considering B3LYP-D3 method may have overestimated the dispersion contribution [58,59] and reflected the free-energy barrier of B–H activation (TS8a/b) inaccurately, the RDS free-energy barriers, reaction rate constants and half-lives derived from LC-ωPBE method are closest to corresponding experimental data. Additionally, the diastereoselective ratio (dr) of P1a to P1b predicted by LC-ωPBE method is about 3.9:1, also coincides best with corresponding experimental results (Table 2).
For further confirmation of TS8a/b (or TS9a/b for B3LYP-D3 method)’s RDS character, full optimizations about stationary points lying on the PESs from M1+R3 to INT8 were performed at PCM-CAM-B3LYP/DZVP, PCM-B3LYP/DZVP and PCM-B3LYP-D3/DZVP levels. Corresponding Gibbs free-energy barriers of transition states TS1-TS7 are summarized in Table 3, with detailed potential energy profiles shown in Figure S8 and relative Gibbs free energies summarized in Table S3. Except for the free-energy barrier of TS6 employing B3LYP-D3 method is of equivalence to that of TS9a/b (22.4 vs. 22.1–23.1 kcal·mol−1), all other free-energy barriers of transition states TS1-TS7 are much lower than TS8a/b. These results obtained by employing LC-ωPBE, CAM-B3LYP and B3LYP methods illustrate that TS8a/b is indeed the RDS, and the B–H activation process has a decisive influence on the overall rate of this reaction. Further single-point calculations employing CAM-B3LYP, B3LYP, and B3LYP-D3 methods, combined with a larger TZVP basis set also show very small deviation in energy from the DZVP optimized ones (Figure S8), indicating the rationality of employing DZVP basis set in current simulation again.
Finally, to investigate the rationality of replacing Cs2CO3 with K2CO3 in our simulation, Path a and b employing Cs2CO3 have been tested at PCM-LC-ωPBE/DZVP (SDD [61] for Cs) level (Entry 2 in Figure S4), with corresponding energetic results presented in square brackets in Figure 3 and Figure 6 respectively. Although non-negligible energy differences for stationary points can be observed when K2CO3 is employed in place of Cs2CO3, the mechanism trends in these two cases coincide well with each other. Results based on PCM-LC-ωPBE/DZVP optimization employing both Cs2CO3 and K2CO3 can predict rational dr ratio of P1a:P1b (3.3:1 and 3.9:1 respectively, Entry 1–2); however, the half-lives derived from RDS barriers employing Cs2CO3 additive deviate two orders of magnitude from corresponding experimental time (12 h). Further optimization at PCM-LC-ωPBE/TZVP (SDD for Cs) level (Entry 3–4) give out similar mechanistic and energetic results with the DZVP ones, indicating no necessity for full optimization employing TZVP basis set in current simulation. Taking both the predicted half-life and dr value into account, the PCM-LC-ωPBE/DZVP level’s results by employing K2CO3 additive coincide best with corresponding experimental time and yield (80% after 12 h).

4. Conclusions

In summary, density functional theory (DFT) at PCM-LC-ωPBE/DZVP, PCM-CAM-B3LYP/DZVP, PCM-B3LYP/DZVP, and PCM-B3LYP-D3/DZVP levels have been employed to conduct computational investigations on Ni(PMe3)2-mediated reaction of o-carboranylzirconacycle (R1), n-hexene (R2) and 2-bromophenyltrimethylsilylacetylene (R3) in toluene solution. The following conclusions can be drawn: (1) This reaction is a multistep process, in which more than an intermediate such as nickelacyclopentane, nickelacycloheptene, nickelacyclohexane, and dihydrofulvenocarborane intermediates are involved. With the assistance of Cs2CO3 additive, the rate-determining B–H activation of dihydrofulvenocarborane intermediate INT8 are smoothly achieved at room temperature. Finally, the o-carboranyl cage B–C(sp2) phenyl coupling and corresponding C,C,B-substituted o-carborane-fused tricyclics (P1a/b) are obtained through reduction elimination, accompanying by regeneration of the Ni(PMe3)2 catalyst. (2) The Cs2CO3 additive is directly involved in o-carborane’s B–H activation, and it can dramatically reduce the RDS’s free-energy barriers through stabilizing corresponding transition structures (TS8a/b). It is deemed that the addition of Cs2CO3 ensures this reaction’s smooth proceeding at room temperature. (3) Computational results obtained by employing LC-ωPBE, CAM-B3LYP, and B3LYP functionals indicate the activation of B(11)–H or B(17)–H bonds in dihydrofulvenocarborane intermediate INT8 is the RDS of the entire reaction. The Gibbs free-energy barriers for RDS (TS8a/b) at PCM-LC-ωPBE/DZVP level is calculated to be 23.1–23.9 kcal·mol−1, transferring to half-lives of 3.9–15.1 h. The predicted half-lives exhibit small deviation from experimental yield and time (80% in 12 h). The diastereoselective ratio (dr) of P1a to P1b predicted by LC-ωPBE method is about 3.9:1, also reproduces corresponding experimental observation (P1a:P1b ≈ 1:1) well.

Supplementary Materials

The following are available online at https://www.mdpi.com/2073-4344/9/6/548/s1, Figure S1: M1’s formation from R1+CAT1+R2, Figures S2 and S6: Optimized structures and key geometrical parameters for stationary points, Figure S3: Relative Gibbs free energies of M2, Figure S4: PESs employing Cs2CO3 and K2CO3, Figure S5: Part PESs for Path a3 and a4, Figure S7: PESs for B(11)/B(17)–H activation in INT8, obtained at different computational levels, Figure S8: PESs for intermediate INT8’s formation from M1+R3, obtained at different computational levels, Table S1: Free-energy barriers and corresponding kinetic data for transition states TS1-TS7 and TS8a, Tables S2–S3: Relative Gibbs free energies for stationary points on Path a and b, obtained at different computational levels, Tables S4, S7 and S13: Optimized Cartesian coordinates for stationary points, Tables S5, S8 and S14: Vibrational frequencies for stationary points, Tables S6, S9–S12 and S15–S17: Energetic results for stationary points, obtained at different computational levels.

Author Contributions

Data curation, W.-H.M., W.-Z.L., Q.H. and R.-J.C.; Funding acquisition, W.-H.M.; Project administration, W.-H.M.; Visualization, W.-Z.L.; Writing-original draft, W.-H.M. and W.-Z.L.; Writing-review and editing, W.-H.M., L.-J.D., P.L. and Q.H.

Acknowledgments

The authors acknowledge financial supports from the National Natural Science Foundation of China (grant number 21763033 and 21363028), as well as software supports from De-Cai Fang in College of Chemistry, Beijing Normal University.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Chen, G.; Yang, J.; Lu, G.; Liu, P.C.; Chen, Q.; Xie, Z.; Wu, C. One Stone Kills Three Birds: Novel Boron-Containing Vesicles for Potential BNCT, Controlled Drug Release, and Diagnostic Imaging. Mol. Pharm. 2014, 11, 3291–3299. [Google Scholar] [CrossRef] [PubMed]
  2. Guo, J.; Liu, D.; Zhang, J.; Zhang, J.; Miao, Q.; Xie, Z. o-Carborane Functionalized Pentacenes: Synthesis, Molecular Packing and Ambipolar Organic Thin-film Transistors. Chem. Commun. 2015, 51, 12004–12007. [Google Scholar] [CrossRef] [PubMed]
  3. Jin, G.F.; Hwang, J.-H.; Lee, J.-D.; Wee, K.-R.; Suh, I.-H.; Kang, S.O. A Three-Dimensional π-Electron Acceptor, Tri-Phenyl-o-Carborane, Bearing a Rigid Conformation with End-On Phenyl Units. Chem. Commun. 2013, 49, 9398–9400. [Google Scholar] [CrossRef] [PubMed]
  4. Cioran, A.M.; Musteti, A.D.; Teixidor, F.; Krpetic, Ž.; Prior, I.A.; He, Q.; Kiely, C.J.; Brust, M.; Viñas, C. Mercaptocarborane-Capped Gold Nanoparticles: Electron Pools and Ion Traps with Switchable Hydrophilicity. J. Am. Chem. Soc. 2012, 134, 212–221. [Google Scholar] [CrossRef] [PubMed]
  5. Scholz, M.; Hey-Hawkins, E. Carbaboranes as Pharmacophores: Properties, Synthesis, and Application Strategies. Chem. Rev. 2011, 111, 7035–7062. [Google Scholar] [CrossRef] [PubMed]
  6. Jude, H.; Disteldorf, H.; Fischer, S.; Wedge, T.; Hawkridge, A.M.; Arif, A.M.; Hawthorne, M.F.; Muddiman, D.C.; Stang, P.J. Coordination-Driven Self-Assemblies with a Carborane Backbone. J. Am. Chem. Soc. 2005, 127, 12131–12139. [Google Scholar] [CrossRef]
  7. Grimes, R.N. Carboranes in the Chemist’s Toolbox. Dalton Trans. 2015, 44, 5939–5956. [Google Scholar] [CrossRef]
  8. Qiu, Z.; Xie, Z. Generation and Reactivity of o-Carborynes. Dalton Trans. 2014, 43, 4925–4934. [Google Scholar] [CrossRef]
  9. Tang, C.; Xie, Z. Nickel-Catalyzed Cross-Coupling Reactions of o-Carboranyl with Aryl Iodides: Facile Synthesis of 1-Aryl-o-Carboranes and 1,2-Diaryl-o-Carboranes. Angew. Chem. Int. Ed. 2015, 54, 7662–7665. [Google Scholar] [CrossRef]
  10. Lyu, H.; Quan, Y.; Xie, Z. Palladium-Catalyzed Direct Dialkenylation of Cage B-H Bonds in o-Carboranes Through Cross-Coupling Reactions. Angew. Chem. Int. Ed. 2015, 54, 10623–10626. [Google Scholar] [CrossRef]
  11. Lyu, H.; Quan, Y.; Xie, Z. Transition Metal Catalyzed Direct Amination of the Cage B(4)-H Bond in o-Carboranes: Synthesis of Tertiary, Secondary, and Primary o-Carboranyl Amines. J. Am. Chem. Soc. 2016, 138, 12727–12730. [Google Scholar] [CrossRef] [PubMed]
  12. Lyu, H.; Quan, Y.; Xie, Z. Rhodium-Catalyzed Regioselective Hydroxylation of Cage B-H Bonds of o-Carboranes with O2 or Air. Angew. Chem. Int. Ed. 2016, 55, 11840–11844. [Google Scholar] [CrossRef] [PubMed]
  13. Quan, Y.; Xie, Z. Palladium-Catalyzed Regioselective Diarylation of o-Carboranes by Direct Cage B-H Activation. Angew. Chem. Int. Ed. 2016, 55, 1295–1298. [Google Scholar] [CrossRef] [PubMed]
  14. Zhao, D.; Xie, Z. Recent Advances in the Chemistry of Carborynes. Coordin. Chem. Rev. 2016, 314, 14–33. [Google Scholar] [CrossRef]
  15. Ren, S.; Qiu, Z.; Xie, Z. Transition-Metal-Promoted or -Catalyzed Exocyclic Alkyne Insertion via Zirconacyclopentene with Carborane Auxiliary: Formation of Symmetric or Unsymmetric Benzocarboranes. J. Am. Chem. Soc. 2012, 134, 3242–3254. [Google Scholar] [CrossRef] [PubMed]
  16. Ren, S.; Qiu, Z.; Xie, Z. Three-Component [2+2+2] Cycloaddition of Carboryne, Unactivated Alkene, and Alkyne via Zirconacyclopentane Mediated by Nickel: One-Pot Synthesis of Dihydrobenzocarboranes. Angew. Chem. Int. Ed. 2012, 51, 1010–1013. [Google Scholar] [CrossRef] [PubMed]
  17. Mu, W.-H.; Cheng, R.-J.; Fang, D.-C.; Chass, G.A. The Pivotal Role of Electronics in Preferred Alkene over Alkyne Ni-Carboryne Insertions and Absolute Regioselectivities. Dalton Trans. 2018, 47, 6494–6498. [Google Scholar] [CrossRef]
  18. Zhao, D.; Zhang, J.; Xie, Z. An Unprecedented Formal [5+2] Cycloaddition of Nitrones with o-Carboryne via Tandem [3+2] Cycloaddition/Oxygen Migration/Aromatization Sequence. J. Am. Chem. Soc. 2015, 137, 13938–13942. [Google Scholar] [CrossRef]
  19. Mu, W.-H.; Xia, S.-Y.; Li, J.-X.; Fang, D.-C.; Wei, G.; Chass, G.A. Competing Mechanisms, Substituent Effects, and Regioselectivities of Nickel-Catalyzed [2+2+2] Cycloaddition between Carboryne and Alkynes: A DFT Study. J. Org. Chem. 2015, 80, 9108–9117. [Google Scholar] [CrossRef]
  20. Zhang, J.; Quan, Y.; Lin, Z.; Xie, Z. Insight into Reaction Mechanism of [2+2+1] Cross-Cyclotrimerization of Carboryne with Alkene and Trimethylsilylarylalkyne Mediated by Nickel Complex. Organometallics 2014, 33, 3556–3563. [Google Scholar] [CrossRef]
  21. Huo, R.-P.; Guo, L.-H.; Zhang, F.-Q.; Zhang, X. Multiple Electronic State Mechanism for Carboryne Reaction with Benzene: A DFT Study. Int. J. Quantum Chem. 2017, 117, e25372. [Google Scholar] [CrossRef]
  22. Mu, W.H.; Ma, Y.; Fang, D.C.; Wang, R.; Zhang, H.N. Computational Insights into the Diels-Alder-alike Reactions of 1-Iodo-2-Lithio-o-Carborane with Fulvenes. Acta Chimica Sinica 2018, 76, 55–61. [Google Scholar] [CrossRef]
  23. Zhao, D.; Zhang, J.; Xie, Z. 1,3-Dehydro-o-Carborane: Generation and Reaction with Arenes. Angew. Chem. Int. Ed. 2014, 53, 8488–8491. [Google Scholar] [CrossRef] [PubMed]
  24. Qiu, Z.; Xie, Z. Palladium/Nickel-Cocatalyzed Cycloaddition of 1,3-Dehydro-o-Carborane with Alkynes. Facile Synthesis of C,B-Substituted Carboranes. J. Am. Chem. Soc. 2010, 132, 16085–16093. [Google Scholar] [CrossRef] [PubMed]
  25. Quan, Y.; Qiu, Z.; Xie, Z. Transition-Metal-Mediated Three-Component Cascade Cyclization: Selective Cage B-C(sp2) Coupling of Carborane with Aromatics and Synthesis of Carborane-Fused Tricyclics. J. Am. Chem. Soc. 2014, 136, 7599–7602. [Google Scholar] [CrossRef] [PubMed]
  26. Quan, Y.; Zhang, J.; Xie, Z. Three-Component [2+2+1] Cross-Cyclotrimerization of Carboryne, Unactivated Alkene, and Trimethylsilylalkyne Co-Mediated by Zr and Ni. J. Am. Chem. Soc. 2013, 135, 18742–18745. [Google Scholar] [CrossRef] [PubMed]
  27. Mu, W.-H.; Liu, W.-Z.; Cheng, R.-J.; Fang, D.-C. Electronic Effect-Guided, Palladium-Catalyzed Regioselective B-H Activation and Multistep Diarylation of o-Carboranes with Aryl Iodides. ACS Omega 2019, 4, 465–474. [Google Scholar] [CrossRef]
  28. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
  29. Tawada, Y.; Tsuneda, T.; Yanagisawa, S.; Yanai, T.; Hirao, K. A Long-range-corrected Time-dependent Density Functional Theory. J. Chem. Phys. 2004, 120, 8425–8433. [Google Scholar] [CrossRef]
  30. Vydrov, O.A.; Scuseria, G.E. Assessment of A Long Range Corrected Hybrid Functional. J. Chem. Phys. 2006, 125, 234109. [Google Scholar] [CrossRef]
  31. Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange-correlation Functional Using the Coulomb-attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
  32. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
  33. Becke, A.D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
  34. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
  35. Chai, J.-D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
  36. Godbout, N.; Salahub, D.R.; Andzelm, J.; Wimmer, E. Optimization of Gaussian-type Basis Sets for Local Spin Density Functional Calculations. Part I. Boron Through Neon, Optimization Technique and Validation. Can. J. Chem. 1992, 70, 560–571. [Google Scholar] [CrossRef]
  37. Sosa, C.; Andzelm, J.; Elkin, B.C.; Wimmer, E.; Dobbs, K.D.; Dixon, D.A. A Local Density Functional Study of the Structure and Vibrational Frequencies of Molecular Transition-Metal Compounds. J. Phys. Chem. 1992, 96, 6630–6636. [Google Scholar] [CrossRef]
  38. Schäfer, A.; Horn, H.; Ahlrichs, R. Fully Optimized Contracted Gaussian-Basis Sets for Atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
  39. Schäfer, A.; Huber, C.; Ahlrichs, R. Fully Optimized Contracted Gaussian-Basis Sets of Triple zeta Valence Quality for Atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
  40. Gonzalez, C.; Schlegel, H.B. An Improved Algorithm for Reaction Path Following. J. Chem. Phys. 1989, 90, 2154–2161. [Google Scholar] [CrossRef]
  41. Gonzalez, C.; Schlegel, H.B. Reaction Path Following in Mass-Weighted Internal Coordinates. J. Phys. Chem. 1990, 94, 5523–5527. [Google Scholar] [CrossRef]
  42. Fukui, K. The Path of Chemical Reactions - the IRC Approach. Acc. Chem. Res. 1981, 14, 363–368. [Google Scholar] [CrossRef]
  43. Miertuš, S.; Scrocco, E.; Tomasi, J. Electrostatic Interaction of a Solute with a Continuum. A Direct Utilizaion of AB Initio Molecular Potentials for the Prevision of Solvent Effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
  44. York, D.M.; Karplus, M. A Smooth Solvation Potential Based on the Conductor-Like Screening Model. J. Phys. Chem. 1999, 103, 11060–11079. [Google Scholar] [CrossRef]
  45. Tao, J.-Y.; Mu, W.-H.; Chass, G.A.; Tang, T.-H.; Fang, D.-C. Balancing the Atomic Waistline: Isodensity-Based SCRF Radii for Main-Group Elements and Transition Metals. Int. J. Quantum Chem. 2013, 113, 975–984. [Google Scholar] [CrossRef]
  46. Fang, D.-C. THERMO Program; Beijing Normal University: Beijing, China, 2013; This program can generate thermodynamic data in solution under given temperature, based on normally terminated Gaussian jobs with “freq” and “volume” keywords. [Google Scholar]
  47. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular Interactions from a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  48. Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural Population Analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
  49. Carpenter, J.E.; Weinhold, F.J. Analysis of the Geometry of the Hydroxymethyl Radical by the “Different Hybrids for Different Spins” Natural Bond Orbital Procedure. J. Mol. Struc.-THEOCHEM 1988, 169, 41–62. [Google Scholar] [CrossRef]
  50. Hostaš, J.; Řezáč, J. Accurate DFT-D3 Calculations in a Small Basis Set. J. Chem. Theory Comput. 2017, 13, 3575–3585. [Google Scholar] [CrossRef]
  51. Masson-Makdissi, J.; Vandavasi, J.K.; Newman, S.G. Switchable Selectivity in the Pd-Catalyzed Alkylative Cross-Coupling of Esters. Org. let. 2018, 20, 4094–4098. [Google Scholar] [CrossRef]
  52. Kim, S.W.; Schwartz, L.A.; Zbieg, J.R.; Stivala, C.E.; Krische, M.J. Regio- and Enantioselective Iridium-Catalyzed Amination of Racemic Branched Alkyl-Substituted Allylic Acetates with Primary and Secondary Aromatic and Heteroaromatic Amines. J. Am. Chem. Soc. 2019, 141, 671–676. [Google Scholar] [CrossRef]
  53. Dong, C.-C.; Xiang, J.-F.; Xu, L.-J.; Gong, H.-Y. From CO2 to 4H-Quinolizin-4-ones: A One-Pot Multicomponent Approach via Ag2O/Cs2CO3 Orthogonal Tandem Catalysis. J. Org. Chem. 2018, 83, 9561–9567. [Google Scholar] [CrossRef] [PubMed]
  54. Koga, Y.; Kaneda, T.; Saito, Y.; Murakami, K.; Itami, K. Synthesis of Partially and Fully Fused Polyaromatics by Annulative Chlorophenylene Dimerization. Science 2018, 359, 435–439. [Google Scholar] [CrossRef]
  55. Swyka, R.A.; Zhang, W.; Richardson, J.; Ruble, J.C.; Krische, M.J. Rhodium-Catalyzed Aldehyde Arylation via Formate-Mediated Transfer Hydrogenation: Beyond Metallic Reductants in Grignard/Nozaki-Hiyami-Kishi-Type Addition. J. Am. Chem. Soc. 2019, 141, 1828–1832. [Google Scholar] [CrossRef] [PubMed]
  56. Baker, J.; Scheiner, A.; Andzelm, J. Spin contamination in density functional theory. Chem. Phys. Lett. 1993, 216, 380–388. [Google Scholar] [CrossRef]
  57. Quan, Y.; Xie, Z. Palladium-Catalyzed Regioselective Intramolecular Coupling of o-Carborane with Aromatics via Direct Cage B-H Activation. J. Am. Chem. Soc. 2015, 137, 3502–3505. [Google Scholar] [CrossRef] [PubMed]
  58. Ding, L.; Ishida, N.; Murakami, M.; Morokuma, K. Sp3-sp2 vs. sp3-sp3 C-C Site Selectivity in Rh-Catalyzed Ring Opening of Benzocyclobutenol: A DFT Study. J. Am. Chem. Soc. 2014, 136, 169–178. [Google Scholar] [CrossRef] [PubMed]
  59. Li, Y.; Fang, D.-C. DFT Calculations on Kinetic Data for Some [4+2] Reactions in Solution. Phys. Chem. Chem. Phys. 2014, 16, 15224–15230. [Google Scholar] [CrossRef] [PubMed]
  60. Armstrong, A.; Boto, R.A.; Dingwall, P.; Contreras-Garcia, J.; Harvey, M.J.; Mason, N.J.; Rzepa, H.S. The Houk-List transition States for Organocatalytic Mechanisms Revisited. Chem. Sci. 2014, 5, 2057–2071. [Google Scholar] [CrossRef]
  61. Fuentealba, P.; Preuss, H.; Stoll, H.; Szentpály, L.V. A Proper Account of Core-polarization with Pseudopotentials: Single Valence-Electron Alkali Compounds. Chem. Phys. Lett. 1982, 89, 418–422. [Google Scholar] [CrossRef]
Catalysts 09 00548 sch001 550
Scheme 1. Nickel-mediated reaction of o-carboranylzirconacycle (R1), n-hexene (R2) and 2-bromophenyltrimethylsilylacetylene (R3).
Scheme 1. Nickel-mediated reaction of o-carboranylzirconacycle (R1), n-hexene (R2) and 2-bromophenyltrimethylsilylacetylene (R3).
Catalysts 09 00548 sch001
Catalysts 09 00548 sch002 550
Scheme 2. Formation mechanism of the dihydrofulvenocarborane intermediate INT8 from o-carborane compound M1+R3.
Scheme 2. Formation mechanism of the dihydrofulvenocarborane intermediate INT8 from o-carborane compound M1+R3.
Catalysts 09 00548 sch002
Catalysts 09 00548 g001 550
Figure 1. Relative Gibbs free energies (298 K, kcal·mol−1) for the formation of intermediate INT8 from M1+R3, obtained at PCM-LC-ωPBE/DZVP level in toluene solution. The single-point calculation results obtained by employing TZVP basis set are presented in parentheses for comparison.
Figure 1. Relative Gibbs free energies (298 K, kcal·mol−1) for the formation of intermediate INT8 from M1+R3, obtained at PCM-LC-ωPBE/DZVP level in toluene solution. The single-point calculation results obtained by employing TZVP basis set are presented in parentheses for comparison.
Catalysts 09 00548 g001
Catalysts 09 00548 g002 550
Figure 2. Optimized structures and key geometrical parameters (bond length in Å) for stationary points involved in the formation of intermediate INT8 from M1+R3. For clarity, all noncritical atoms especially hydrogens were made transparent, and all structures not referred directly in the text were presented in Figure S2.
Figure 2. Optimized structures and key geometrical parameters (bond length in Å) for stationary points involved in the formation of intermediate INT8 from M1+R3. For clarity, all noncritical atoms especially hydrogens were made transparent, and all structures not referred directly in the text were presented in Figure S2.
Catalysts 09 00548 g002
Catalysts 09 00548 g003 550
Figure 3. Most probable mechanism and relative Gibbs free energies (298 K, kcal·mol−1) for B(11)–H activation and cage B–C(sp2) coupling of intermediate INT8, obtained at PCM-LC-ωPBE/DZVP level in toluene solution. Free-energy results obtained by employing Cs2CO3 are presented in square brackets for comparison.
Figure 3. Most probable mechanism and relative Gibbs free energies (298 K, kcal·mol−1) for B(11)–H activation and cage B–C(sp2) coupling of intermediate INT8, obtained at PCM-LC-ωPBE/DZVP level in toluene solution. Free-energy results obtained by employing Cs2CO3 are presented in square brackets for comparison.
Catalysts 09 00548 g003
Catalysts 09 00548 g004 550
Figure 4. Optimized structures and key geometrical parameters (bond length in Å) for stationary points involved in the B(11)–H activation and cage B–C(sp2) coupling process of intermediate INT8. For clarity, all noncritical atoms especially hydrogens were made transparent, and all structures not referred directly in the text were presented in Figure S2.
Figure 4. Optimized structures and key geometrical parameters (bond length in Å) for stationary points involved in the B(11)–H activation and cage B–C(sp2) coupling process of intermediate INT8. For clarity, all noncritical atoms especially hydrogens were made transparent, and all structures not referred directly in the text were presented in Figure S2.
Catalysts 09 00548 g004
Catalysts 09 00548 g005 550
Figure 5. Another two paths (Path a1 and a2) and relative Gibbs free energies (298 K, kcal·mol−1) for B(11)–H activation of intermediate INT8, obtained at PCM-LC-ωPBE/DZVP level in toluene solution. Path a is plotted in grey dotted line for comparison.
Figure 5. Another two paths (Path a1 and a2) and relative Gibbs free energies (298 K, kcal·mol−1) for B(11)–H activation of intermediate INT8, obtained at PCM-LC-ωPBE/DZVP level in toluene solution. Path a is plotted in grey dotted line for comparison.
Catalysts 09 00548 g005
Catalysts 09 00548 g006 550
Figure 6. Probable mechanism and relative Gibbs free energies (298 K, kcal·mol−1) for B(17)–H activation and cage B–C(sp2) coupling of intermediate INT8, obtained at PCM-LC-ωPBE/DZVP level in toluene solution. Path a is plotted in grey dotted line for comparison. Free-energy results obtained by employing Cs2CO3 are presented in square brackets for comparison.
Figure 6. Probable mechanism and relative Gibbs free energies (298 K, kcal·mol−1) for B(17)–H activation and cage B–C(sp2) coupling of intermediate INT8, obtained at PCM-LC-ωPBE/DZVP level in toluene solution. Path a is plotted in grey dotted line for comparison. Free-energy results obtained by employing Cs2CO3 are presented in square brackets for comparison.
Catalysts 09 00548 g006
Table
Table 1. NBO charge population of key atoms in intermediate INT8 and K2CO3 additive, obtained at PCM-LC-ωPBE/DZVP//DZVP level in toluene solution (unit: ē).
Table 1. NBO charge population of key atoms in intermediate INT8 and K2CO3 additive, obtained at PCM-LC-ωPBE/DZVP//DZVP level in toluene solution (unit: ē).
Catalysts 09 00548 i001 NBO charge Catalysts 09 00548 i002
Br(10)−0.480
H(12)+0.041
O(13)−1.055
K(16)+0.932
Table
Table 2. Free-energy barriers (in kcal·mol−1) and corresponding kinetic data for RDSs (TS8a/b or TS9a/b).
Table 2. Free-energy barriers (in kcal·mol−1) and corresponding kinetic data for RDSs (TS8a/b or TS9a/b).
MethodsLC-ωPBECAM-B3LYPB3LYPB3LYP-D3
Free-energy barriers (ΔΔG, kcal·mol−1)TS8a23.124.826.715.2
TS8b23.926.929.614.3
TS9a14.210.33.122.1
TS9b13.48.96.923.1
kRDS,a (L·mol−1·s−1)7.113 × 10−54.030 × 10−61.629 × 10−73.850 × 10−4
kRDS,b (L·mol−1·s−1)1.842 × 10−51.162 × 10−71.216 × 10−97.113 × 10−5
t1/2,RDS,a (h)3.905 × 1006.893 × 1011.705 × 1035.002 × 10−1
t1/2,RDS,b (h)1.508 × 1012.390 × 1032.283 × 1052.707 × 100
drCalc.3.9:135:1134:15.4:1
drExpt.1:1
Table
Table 3. Free-energy barriers (ΔΔG, kcal·mol−1) for transition states TS1-TS7, obtained at PCM- LC-ωPBE/DZVP (denoted LC-ωPBE), PCM-CAM-B3LYP/DZVP (denoted CAM-B3LYP), PCM-B3LYP/DZVP (denoted B3LYP) and PCM-B3LYP-D3/DZVP (denoted B3LYP-D3) levels in toluene solution at 298 K.
Table 3. Free-energy barriers (ΔΔG, kcal·mol−1) for transition states TS1-TS7, obtained at PCM- LC-ωPBE/DZVP (denoted LC-ωPBE), PCM-CAM-B3LYP/DZVP (denoted CAM-B3LYP), PCM-B3LYP/DZVP (denoted B3LYP) and PCM-B3LYP-D3/DZVP (denoted B3LYP-D3) levels in toluene solution at 298 K.
Transition StatesFree-energy Barriers (ΔΔG, kcal·mol−1)
LC-ωPBECAM-B3LYPB3LYPB3LYP-D3
TS15.912.219.110.8
TS214.416.014.312.9
TS310.514.915.615.2
TS42.41.01.62.1
TS514.618.819.317.7
TS617.923.922.322.4
TS74.65.44.72.1

Share and Cite

MDPI and ACS Style

Mu, W.-H.; Liu, W.-Z.; Cheng, R.-J.; Dou, L.-J.; Liu, P.; Hao, Q. Computational Investigation of Nickel-Mediated B–H Activation and Regioselective Cage B–C(sp2) Coupling of o-Carborane. Catalysts 2019, 9, 548. https://doi.org/10.3390/catal9060548

AMA Style

Mu W-H, Liu W-Z, Cheng R-J, Dou L-J, Liu P, Hao Q. Computational Investigation of Nickel-Mediated B–H Activation and Regioselective Cage B–C(sp2) Coupling of o-Carborane. Catalysts. 2019; 9(6):548. https://doi.org/10.3390/catal9060548

Chicago/Turabian Style

Mu, Wei-Hua, Wen-Zhu Liu, Rui-Jiao Cheng, Li-Juan Dou, Pin Liu, and Qiang Hao. 2019. "Computational Investigation of Nickel-Mediated B–H Activation and Regioselective Cage B–C(sp2) Coupling of o-Carborane" Catalysts 9, no. 6: 548. https://doi.org/10.3390/catal9060548

APA Style

Mu, W. -H., Liu, W. -Z., Cheng, R. -J., Dou, L. -J., Liu, P., & Hao, Q. (2019). Computational Investigation of Nickel-Mediated B–H Activation and Regioselective Cage B–C(sp2) Coupling of o-Carborane. Catalysts, 9(6), 548. https://doi.org/10.3390/catal9060548

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop