Freeze Concentration of Aqueous [DBNH][OAc] Ionic Liquid Solution
Abstract
:1. Introduction
2. Materials and Methods
2.1. Differential Scanning Calorimetry (DSC)
2.2. Water Activity Coefficient
| activity coefficient of water, | |
| mole fraction of water, | |
| enthalpy of fusion for water at 273.15 K (6009.5 J/mol), | |
| heat capacity difference between water and solid ice (J/molK), | |
| R | universal gas constant (8.3143 J/molK), |
| freezing point of pure water (273.15 K), | |
| freezing point of aqueous ionic liquid solution obtained by DSC (K). |
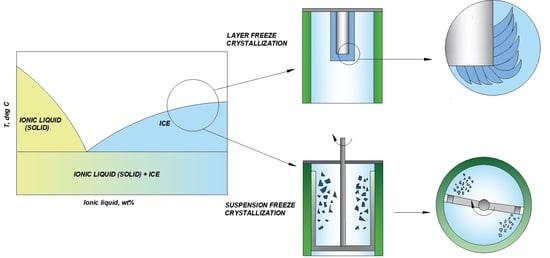
2.3. Layer Freeze Crystallization
2.4. Suspension Freeze Crystallization
2.5. Determining Distribution Coefficient and Crystal Yield
| mass of the pure ice (kg), | |
| mass of the water in initial solution (kg). |
| Cimp | concentration of ionic liquid in ice (kg [DBNH][OAc]/kg ice), |
| C0 | initial concentration of ionic liquid in solution (kg [DBNH][OAc]/kg solution). |
3. Results
3.1. Phase Equilibria of Binary [DBNH][OAc] and Water System
- Region 1: At lower water content, mixtures were solid at ambient temperature.
- Region 2: No crystallization upon cooling and no recrystallization upon heating were observed, but glass transitions were measured at −73 °C
- Region 3: Crystallization of mixtures occurred upon heating. The mixtures underwent the transitions in following order: glass transition, recrystallization, and finally melting.
- Region 4: Mixtures neither crystallized nor underwent glass transition when they were cooled to −80 °C and heated up to 25 °C during DSC analyses.
- Region 5: For the mixtures with water content was greater than 54.3 wt.%, crystallization occurred upon cooling and melting upon heating. The melting temperatures acquired were used to construct the liquidus line of ice.
3.2. Layer Freeze Crystallization Results
3.3. Suspension Freeze Crystallization Results
4. Discussion
5. Conclusions
- Based on obtained solid–liquid equilibria, it was concluded that melt crystallization can be employed as a concentration method for aqueous [DBNH][OAc] solutions with water content higher than 54.3 wt.%.
- Water activity coefficient results calculated in mole fraction range between 0 and 0.08 showed that [DBNH][OAc] solutions are non-ideal solutions with an attractive interaction between [DBNH][OAc] and water molecules.
- Single-step suspension freeze crystallization is a more suitable concentration method for aqueous [DNBH][OAc] solutions than single-step layer freeze crystallization, based on the comparison between ice crystal yield and ice purity of these two freeze crystallization methods.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ulrich, J. Introduction. In Melt Crystallization: Fundamentals, Equipment and Applications; Ulrich, J., Glade, H., Eds.; Berichte aus der Verfahrenstechnik; Shaker: Aachen, Germany, 2003; pp. 1–6. [Google Scholar]
- Parviainen, A.; Wahlström, R.; Liimatainen, U.; Liitiä, T.; Rovio, S.; Helminen, J.K.J.; Hyväkkö, U.; King, A.W.T.; Suurnäkki, A.; Kilpeläinen, I. Sustainability of Cellulose Dissolution and Regeneration in 1,5-Diazabicyclo[4.3.0]Non−5-Enium Acetate: A Batch Simulation of the IONCELL-F Process. RSC Adv. 2015, 5, 69728–69737. [Google Scholar] [CrossRef] [Green Version]
- Wendler, F.; Todi, L.-N.; Meister, F. Thermostability of Imidazolium Ionic Liquids as Direct Solvents for Cellulose. Thermochim. Acta 2012, 528, 76–84. [Google Scholar] [CrossRef]
- Vigier, K.D.O.; Chatel, G.; Jérôme, F. Contribution of Deep Eutectic Solvents for Biomass Processing: Opportunities, Challenges, and Limitations. ChemCatChem 2015, 7, 1250–1260. [Google Scholar] [CrossRef]
- Freire, M.G.; Neves, C.M.S.S.; Marrucho, I.M.; Coutinho, J.A.P.; Fernandes, A.M. Hydrolysis of Tetrafluoroborate and Hexafluorophosphate Counter Ions in Imidazolium-Based Ionic Liquids. J. Phys. Chem. A 2010, 114, 3744–3749. [Google Scholar] [CrossRef] [PubMed]
- Meine, N.; Benedito, F.; Rinaldi, R. Thermal Stability of Ionic Liquids Assessed by Potentiometric Titration. Green Chem. 2010, 12, 1711. [Google Scholar] [CrossRef]
- Ahmad, W.; Ostonen, A.; Jakobsson, K.; Uusi-Kyyny, P.; Alopaeus, V.; Hyväkkö, U.; King, A.W.T. Feasibility of Thermal Separation in Recycling of the Distillable Ionic Liquid [DBNH][OAc] in Cellulose Fiber Production. Chem. Eng. Res. Des. 2016, 114, 287–298. [Google Scholar] [CrossRef]
- Kakko, T.; King, A.W.T.; Kilpeläinen, I. Homogenous Esterification of Cellulose Pulp in [DBNH][OAc]. Cellulose 2017, 24, 5341–5354. [Google Scholar] [CrossRef] [Green Version]
- Hanabusa, H.; Izgorodina, E.I.; Suzuki, S.; Takeoka, Y.; Rikukawa, M.; Yoshizawa-Fujita, M. Cellulose-Dissolving Protic Ionic Liquids as Low Cost Catalysts for Direct Transesterification Reactions of Cellulose. Green Chem. 2018, 20, 1412–1422. [Google Scholar] [CrossRef]
- Ulrich, J.; Bülau, H.C. Melt Crystallization. In Handbook of Industrial Crystallization, 2nd ed.; Myerson, A.S., Ed.; Elsevier Science and Technology: Oxford, UK, 2001; pp. 161–180, ProQuest Ebook Central; Available online: https://ebookcentral.proquest.com/lib/aalto-ebooks/detail.action?docID=317222 (accessed on 31 January 2020).
- Lewis, A.; Seckler, M.; Kramer, H.J.M.; van Rosmalen, G. Industrial Crystallization: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2015; pp. 261–281. [Google Scholar]
- Liu, Y.; Meyer, A.S.; Nie, Y.; Zhang, S.; Thomsen, K. Low Energy Recycling of Ionic Liquids via Freeze Crystallization during Cellulose Spinning. Green Chem. 2018, 20, 493–501. [Google Scholar] [CrossRef]
- Parviainen, A.; King, A.W.T.; Mutikainen, I.; Hummel, M.; Selg, C.; Hauru, L.K.J.; Sixta, H.; Kilpeläinen, I. Predicting Cellulose Solvating Capabilities of Acid-Base Conjugate Ionic Liquids. ChemSusChem 2013, 6, 2161–2169. [Google Scholar] [CrossRef] [PubMed]
- Stepan, A.M.; Michud, A.; Hellstén, S.; Hummel, M.; Sixta, H. IONCELL-P&F: Pulp Fractionation and Fiber Spinning with Ionic Liquids. Ind. Eng. Chem. Res. 2016, 55, 8225–8233. [Google Scholar] [CrossRef]
- Hauru, L.K.J.; Hummel, M.; Michud, A.; Sixta, H. Dry Jet-Wet Spinning of Strong Cellulose Filaments from Ionic Liquid Solution. Cellulose 2014, 21, 4471–4481. [Google Scholar] [CrossRef]
- Ma, Y.; Stubb, J.; Kontro, I.; Nieminen, K.; Hummel, M.; Sixta, H. Filament Spinning of Unbleached Birch Kraft Pulps: Effect of Pulping Intensity on the Processability and the Fiber Properties. Carbohydr. Polym. 2018, 179, 145–151. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asaadi, S.; Hummel, M.; Ahvenainen, P.; Gubitosi, M.; Olsson, U.; Sixta, H. Structural Analysis of Ioncell-F Fibres from Birch Wood. Carbohydr. Polym. 2018, 181, 893–901. [Google Scholar] [CrossRef] [PubMed]
- Hauru, L.K.J.; Hummel, M.; Nieminen, K.; Michud, A.; Sixta, H. Cellulose Regeneration and Spinnability from Ionic Liquids. Soft Matter 2016, 12, 1487–1495. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lê, H.Q.; Sixta, H.; Hummel, M. Ionic Liquids and Gamma-Valerolactone as Case Studies for Green Solvents in the Deconstruction and Refining of Biomass. Curr. Opin. Green Sustain. Chem. 2019, 18, 20–24. [Google Scholar] [CrossRef]
- Gabbott, P. A Practical Introduction to Differential Scanning Calorimetry. In Principles and Applications of Thermal Analysis; Gabbott, P., Ed.; Blackwell Publishing Ltd.: Oxford, UK, 2008; pp. 1–50. [Google Scholar] [CrossRef]
- Gmehling, J.; Kolbe, B.; Kleiber, M.; Rarey, J. Chemical Thermodynamics for Process. Simulation; Wiley-VCH Verlag & Co. KGaA: Weinheim, Germany, 2012; pp. 405–437. [Google Scholar]
- Sippola, H.; Taskinen, P. Activity of Supercooled Water on the Ice Curve and Other Thermodynamic Properties of Liquid Water up to the Boiling Point at Standard Pressure. J. Chem. Eng. Data 2018, 63, 2986–2998. [Google Scholar] [CrossRef] [PubMed]











© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osmanbegovic, N.; Yuan, L.; Lorenz, H.; Louhi-Kultanen, M. Freeze Concentration of Aqueous [DBNH][OAc] Ionic Liquid Solution. Crystals 2020, 10, 147. https://doi.org/10.3390/cryst10030147
Osmanbegovic N, Yuan L, Lorenz H, Louhi-Kultanen M. Freeze Concentration of Aqueous [DBNH][OAc] Ionic Liquid Solution. Crystals. 2020; 10(3):147. https://doi.org/10.3390/cryst10030147
Chicago/Turabian StyleOsmanbegovic, Nahla, Lina Yuan, Heike Lorenz, and Marjatta Louhi-Kultanen. 2020. "Freeze Concentration of Aqueous [DBNH][OAc] Ionic Liquid Solution" Crystals 10, no. 3: 147. https://doi.org/10.3390/cryst10030147
APA StyleOsmanbegovic, N., Yuan, L., Lorenz, H., & Louhi-Kultanen, M. (2020). Freeze Concentration of Aqueous [DBNH][OAc] Ionic Liquid Solution. Crystals, 10(3), 147. https://doi.org/10.3390/cryst10030147