EM-detwin: A Program for Resolving Indexing Ambiguity in Serial Crystallography Using the Expectation-Maximization Algorithm
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Implementation of the EM-detwin
2.2. Test Datasets
3. Results
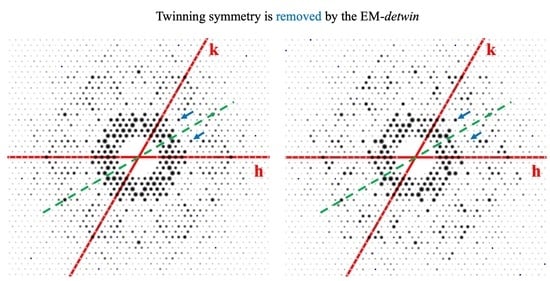
3.1. The Convergence of EM-detwin Program
3.2. Merging Statistics Comparison
3.3. Structure Determination and Refinement with Detwinned Data
3.4. Robustness of the Program
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Neutze, R.; Wouts, R.; van der Spoel, D.; Weckert, E.; Hajdu, J. Potential for biomolecular imaging with femtosecond X-ray pulses. Nature 2000, 406, 752–757. [Google Scholar] [CrossRef] [PubMed]
- Chapman, H.N.; Fromme, P.; Barty, A.; White, T.A.; Kirian, R.A.; Aquila, A.; Hunter, M.S.; Schulz, J.; DePonte, D.P.; Weierstall, U.; et al. Femtosecond X-ray protein nanocrystallography. Nature 2011, 470, 73–77. [Google Scholar] [CrossRef]
- Liu, W.; Wacker, D.; Gati, C.; Han, G.W.; James, D.; Wang, D.; Nelson, G.; Weierstall, U.; Katritch, V.; Barty, A.; et al. Serial femtosecond crystallography of G protein-coupled receptors. Science 2013, 342, 1521–1524. [Google Scholar] [CrossRef] [Green Version]
- Kupitz, C.; Basu, S.; Grotjohann, I.; Fromme, R.; Zatsepin, N.A.; Rendek, K.N.; Hunter, M.S.; Shoeman, R.L.; White, T.A.; Wang, D.; et al. Serial time-resolved crystallography of photosystem II using a femtosecond X-ray laser. Nature 2014, 513, 261–265. [Google Scholar] [CrossRef]
- Park, J.-H.; Yun, J.-H.; Shi, Y.; Han, J.; Li, X.; Jin, Z.; Kim, T.; Park, J.; Park, S.; Liu, H.; et al. Non-Cryogenic Structure and Dynamics of HIV-1 Integrase Catalytic Core Domain by X-ray Free-Electron Lasers. Int. J. Mol. Sci. 2019, 20, 1943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yun, J.H.; Li, X.; Park, J.H.; Wang, Y.; Ohki, M.; Jin, Z.; Lee, W.; Park, S.Y.; Hu, H.; Li, C.; et al. Non-cryogenic structure of a chloride pump provides crucial clues to temperature-dependent channel transport efficiency. J. Biol. Chem. 2019, 294, 794–804. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nogly, P.; James, D.; Wang, D.; White, T.A.; Zatsepin, N.; Shilova, A.; Nelson, G.; Liu, H.; Johansson, L.; Heymann, M.; et al. Lipidic cubic phase serial millisecond crystallography using synchrotron radiation. IUCrJ 2015, 2, 168–176. [Google Scholar] [CrossRef] [PubMed]
- Rossmann, M.G. Serial crystallography using synchrotron radiation. IUCrJ 2014, 1, 84–86. [Google Scholar] [CrossRef] [PubMed]
- Grünbein, M.L.; Kovacs, G.N. Sample delivery for serial crystallography at free-electron lasers and synchrotrons. Acta Crystallogr. Sect. D Struct. Biol. 2019, 75, 178–191. [Google Scholar]
- Weinert, T.; Olieric, N.; Cheng, R.; Brünle, S.; James, D.; Ozerov, D.; Gashi, D.; Vera, L.; Marsh, M.; Jaeger, K.; et al. Serial millisecond crystallography for routine room-temperature structure determination at synchrotrons. Nat. Commun. 2017, 8, 542. [Google Scholar] [CrossRef]
- Wierman, J.L.; Paré-Labrosse, O.; Sarracini, A.; Besaw, J.E.; Cook, M.J.; Oghbaey, S.; Daoud, H.; Mehrabi, P.; Kriksunov, I.; Kuo, A.; et al. Fixed-target serial oscillation crystallography at room temperature. IUCrJ 2019, 6, 305–316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de la Mora, E.; Coquelle, N.; Bury, C.S.; Rosenthal, M.; Holton, J.M.; Carmichael, I.; Garman, E.F.; Burghammer, M.; Colletier, J.-P.; Weik, M. Radiation damage and dose limits in serial synchrotron crystallography at cryo- and room temperatures. Proc. Natl. Acad. Sci. USA 2020, 117, 4142–4151. [Google Scholar] [CrossRef] [Green Version]
- Leslie, A.G.W. Integration of macromolecular diffraction data. Acta Crystallogr. Sect. D Biol. Crystallogr. 1999, 55, 1696–1702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duisenberg, A.J.M. Indexing in single-crystal diffractometry with an obstinate list of reflections. J. Appl. Crystallogr. 1992, 25, 92–96. [Google Scholar] [CrossRef]
- Sauter, N.K.; Grosse-Kunstleve, R.W.; Adams, P.D. Robust indexing for automatic data collection. J. Appl. Crystallogr. 2004, 37, 399–409. [Google Scholar] [CrossRef] [Green Version]
- Brehm, W.; Diederichs, K. Breaking the indexing ambiguity in serial crystallography. Acta Crystallogr. Sect. D 2014, 70, 101–109. [Google Scholar] [CrossRef] [Green Version]
- Gildea, R.J.; Winter, G. Determination of Patterson group symmetry from sparse multi-crystal data sets in the presence of an indexing ambiguity. Acta Crystallogr. Sect. D Struct. Biol. 2018, 74, 405–410. [Google Scholar] [CrossRef] [Green Version]
- Diederichs, K. Dissecting random and systematic differences between noisy composite data sets. Acta Crystallogr. Sect. D Struct. Biol. 2017, 73, 286–293. [Google Scholar] [CrossRef] [Green Version]
- White, T.A.; Kirian, R.A.; Martin, A.V.; Aquila, A.; Nass, K.; Barty, A.; Chapman, H.N. CrystFEL: A software suite for snapshot serial crystallography. J. Appl. Crystallogr. 2012, 45, 335–341. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Spence, J.C.H. The indexing ambiguity in serial femtosecond crystallography (SFX) resolved using an expectation maximization algorithm. IUCrJ 2014, 1, 393–401. [Google Scholar] [CrossRef] [Green Version]
- Wiedorn, M.O.; Oberthür, D.; Bean, R.; Schubert, R.; Werner, N.; Abbey, B.; Aepfelbacher, M.; Adriano, L.; Allahgholi, A.; Al-Qudami, N.; et al. Megahertz serial crystallography. Nat. Commun. 2018, 9, 4025. [Google Scholar] [CrossRef] [Green Version]
- Nogly, P.; Weinert, T.; James, D.; Carbajo, S.; Ozerov, D.; Furrer, A.; Gashi, D.; Borin, V.; Skopintsev, P.; Jaeger, K.; et al. Retinal isomerization in bacteriorhodopsin captured by a femtosecond x-ray laser. Science (80-) 2018, 361, eaat0094. [Google Scholar] [CrossRef] [Green Version]
- Maia, F.R.N.C. The Coherent X-ray Imaging Data Bank. Nat. Methods 2012, 9, 854–855. [Google Scholar] [CrossRef] [PubMed]
- Rose, P.W.; Bi, C.; Bluhm, W.F.; Christie, C.H.; Dimitropoulos, D.; Dutta, S.; Green, R.K.; Goodsell, D.S.; Prlić, A.; Quesada, M.; et al. The RCSB Protein Data Bank: New resources for research and education. Nucleic Acids Res. 2013, 41, 475–482. [Google Scholar] [CrossRef] [PubMed]
- Liebschner, D.; Afonine, P.V.; Baker, M.L.; Bunkoczi, G.; Chen, V.B.; Croll, T.I.; Hintze, B.; Hung, L.W.; Jain, S.; McCoy, A.J.; et al. Macromolecular structure determination using X-rays, neutrons and electrons: Recent developments in Phenix. Acta Crystallogr. Sect. D Struct. Biol. 2019, 75, 861–877. [Google Scholar] [CrossRef] [Green Version]
- Winn, M.D.; Ballard, C.C.; Cowtan, K.D.; Dodson, E.J.; Emsley, P.; Evans, P.R.; Keegan, R.M.; Krissinel, E.B.; Leslie, A.G.W.; McCoy, A.; et al. Overview of the CCP4 suite and current developments. Acta Crystallogr. Sect. D Biol. Crystallogr. 2011, 67, 235–242. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ginn, H.M.; Brewster, A.S.; Hattne, J.; Evans, G.; Wagner, A.; Grimes, J.M.; Sauter, N.K.; Sutton, G.; Stuart, D.I. A revised partiality model and post-refinement algorithm for X-ray free-electron laser data. Acta Crystallogr. Sect. D Biol. Crystallogr. 2015, 71, 1400–1410. [Google Scholar] [CrossRef] [Green Version]
- White, T.A. Post-refinement method for snapshot serial crystallography. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2014, 369, 20130330. [Google Scholar] [CrossRef]
- Sauter, N.K. XFEL diffraction: Developing processing methods to optimize data quality. J. Synchrotron Radiat. 2015, 22, 239–248. [Google Scholar] [CrossRef]



| Parameters | Explanation |
|---|---|
| --spacegroupnum = <n> | The space group number, used to determine twinning operators. |
| --winner-takes-all | If set, the program will use “winner-takes-all” mode to do merging; otherwise, “weighted-merging” will be used for intermediate model merging |
| --highres = <high> | Reject reflections with resolution higher than high Å when calculating correlation coefficients. |
| --lowres = <low> | Reject reflections with resolution lower than low Å when calculating correlation coefficients. |
| --write-assignments = <file> | Write the final re-indexed results to file. |
| --add-operators = <op> | Add specific twin operators. |
| Dataset | Space Group | Bravais Symmetry | Twinning Operators |
|---|---|---|---|
| IN-CCD | P3121 | 321_H | (−h, −k, l), (−k, −h, −l) * |
| BLAC | P3221 | 321_H | (−h, −k, l), (−k, −h, −l) * |
| BR | P63 | 6/m | (k, h, −l) |
| Comparison | Overall R-Factor #/CC1/2†/CCstar* | ||
|---|---|---|---|
| IN-CCD | BLAC | BR | |
| ambigator vs. EM-detwin | 14.21%/ 0.935/0.983 | 9.47%/ 0.989/0.997 | 8.77%/ 0.999/0.999 |
| ambigator vs. twinned | 42.09%/ 0.575/0.854 | 32.60%/ 0.852/0.959 | 35.02%/ 0.905/0.975 |
| EM-detwin vs. twinned | 37.73%/ 0.489/0.810 | 33.23%/ 0.846/0.957 | 30.92%/ 0.915/0.978 |
| Dataset | Algorithm | Resolution Cut-Of | Overall R-Split # | CC1/2 †/CCstar * |
|---|---|---|---|---|
| IN-CCD | ambigator | 2.5Å | 9.26% | 0.989/0.997 |
| EM-detwin | 9.11% | 0.996/0.999 | ||
| BLAC | ambigator | 1.7Å | 29.68% | 0.853/0.959 |
| EM-detwin | 28.59% | 0.872/0.965 | ||
| BR | ambigator | 1.5Å | 10.33% | 0.985/0.996 |
| EM-detwin | 10.24% | 0.985/0.996 |
| Dataset | Algorithm | Resolution | R-Work | R-Free |
|---|---|---|---|---|
| IN-CCD | ambigator | 2.5Å | 0.1840 | 0.2202 |
| EM-detwin | 0.1828 | 0.2230 | ||
| None | 0.2744 | 0.3351 | ||
| BLAC | ambigator | 1.7Å | 0.2308 | 0.2657 |
| EM-detwin | 0.2324 | 0.2620 | ||
| None | 0.2993 | 0.3446 | ||
| BR | ambigator | 1.5Å | 0.1913 | 0.2116 |
| EM-detwin | 0.1927 | 0.2120 | ||
| None | 0.2792 | 0.3077 |
| Algorithms | Indexing Consistency | Correlation Coefficient | ||||
|---|---|---|---|---|---|---|
| IN-CCD | BLAC | BR | IN-CCD | BLAC | BR | |
| ambigator | 99.28% | 86.18% | 99.72% | 0.9854 | 0.9332 | 0.9905 |
| EM-detwin | 96.12% | 88.12% | 98.79% | 0.9275 | 0.9179 | 0.9895 |
| EM-detwin (WTA *) | 95.64% | 57.90% | 98.58% | 0.9280 | 0.7881 | 0.9895 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Liu, H. EM-detwin: A Program for Resolving Indexing Ambiguity in Serial Crystallography Using the Expectation-Maximization Algorithm. Crystals 2020, 10, 588. https://doi.org/10.3390/cryst10070588
Shi Y, Liu H. EM-detwin: A Program for Resolving Indexing Ambiguity in Serial Crystallography Using the Expectation-Maximization Algorithm. Crystals. 2020; 10(7):588. https://doi.org/10.3390/cryst10070588
Chicago/Turabian StyleShi, Yingchen, and Haiguang Liu. 2020. "EM-detwin: A Program for Resolving Indexing Ambiguity in Serial Crystallography Using the Expectation-Maximization Algorithm" Crystals 10, no. 7: 588. https://doi.org/10.3390/cryst10070588
APA StyleShi, Y., & Liu, H. (2020). EM-detwin: A Program for Resolving Indexing Ambiguity in Serial Crystallography Using the Expectation-Maximization Algorithm. Crystals, 10(7), 588. https://doi.org/10.3390/cryst10070588