Extraordinary Response of H-Charged and H-Free Coherent Grain Boundaries in Nickel to Multiaxial Loading
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
3.1. Structure Parameters of 3, 5, and 11 GBs
3.1.1. Clean Grain Boundaries
3.1.2. H-Charged Grain Boundaries
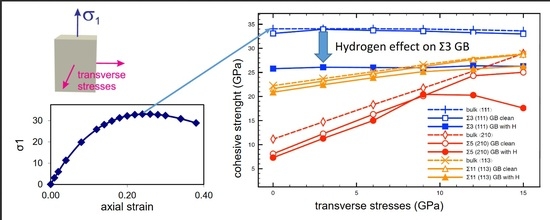
3.2. Cohesive Strength of Hydrogen-Free GBs
3.3. Cohesive Strength of Hydrogen-Charged GBs
3.4. Work of Separation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Seita, M.; Hanson, J.P.; Gradečak, S.; Demkowicz, M.J. The dual role of coherent twin boundaries in hydrogen embrittlement. Nat. Commun. 2015, 6, 6164. [Google Scholar] [CrossRef] [PubMed]
- Koyama, M.; Tasan, C.C.; Akiyama, E.; Tsuzaki, K.; Raabe, D. Hydrogen-assisted decohesion and localized plasticity in dual-phase steel. Acta Mater. 2014, 70, 174–187. [Google Scholar] [CrossRef]
- Geng, W.T.; Freeman, A.J.; Wu, R.; Geller, C.B.; Raynolds, J.E. Embrittling and strengthening effects of hydrogen, boron, and phosphorus on a Σ5 nickel grain boundary. Phys. Rev. B 1999, 60, 7149–7155. [Google Scholar] [CrossRef]
- Xu, X.; Wen, M.; Hu, Z.; Fukuyama, S.; Yokogawa, K. Atomistic process on hydrogen embrittlement of a single crystal of nickel by the embedded atom method. Comput. Mater. Sci. 2002, 23, 131–138. [Google Scholar] [CrossRef]
- Wen, M.; Xu, X.J.; Omura, Y.; Fukuyama, S.; Yokogawa, K. Modeling of hydrogen embrittlement in single crystal Ni. Comput. Mater. Sci. 2004, 30, 202–211. [Google Scholar] [CrossRef]
- Tahir, A.; Janisch, R.; Hartmaier, A. Hydrogen embrittlement of a carbon segregated symmetrical tilt grain boundary in α-Fe. Mater. Sci. Eng. A 2014, 612, 462–467. [Google Scholar] [CrossRef]
- Di Stefano, D.; Mrovec, M.; Elsässer, C. First-principles investigation of hydrogen trapping and diffusion at grain boundaries in nickel. Acta Mater. 2015, 98, 306–312. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Shiga, M.; Kaburaki, H. First-Principles Study on Segregation Energy and Embrittling Potency of Hydrogen in NiΣ5(012) Tilt Grain Boundary. J. Phys. Soc. Jpn. 2004, 73, 441–449. [Google Scholar] [CrossRef]
- Yu, H.; Olsen, J.S.; Alvaro, A.; Olden, V.; He, J.; Zhang, Z. A uniform hydrogen degradation law for high strength steels. Eng. Fract. Mech. 2016, 157, 56–71. [Google Scholar] [CrossRef]
- Alvaro, A.; Jensen, I.T.; Kheradmand, N.; Løvvik, O.; Olden, V. Hydrogen embrittlement in nickel, visited by first principles modeling, cohesive zone simulation and nanomechanical testing. Int. J. Hydrog. Energy 2015, 40, 16892–16900. [Google Scholar] [CrossRef]
- Chen, J.; Dongare, A.M. Role of grain boundary character on oxygen and hydrogen segregation-induced embrittlement in polycrystalline Ni. J. Mater. Sci. 2017, 52, 30–45. [Google Scholar] [CrossRef]
- Tehranchi, A.; Curtin, W.A. Atomistic study of hydrogen embrittlement of grain boundaries in nickel: II. Decohesion. Modell. Simul. Mater. Sci. Eng. 2017, 25, 075013. [Google Scholar] [CrossRef] [Green Version]
- He, S.; Ecker, W.; Pippan, R.; Razumovskiy, V.I. Hydrogen-enhanced decohesion mechanism of the special Sigma5(012)[100] grain boundary in Ni with Mo and C solutes. Comput. Mater. Sci. 2019, 167, 100–110. [Google Scholar] [CrossRef]
- Oriani, R.A. A mechanistic theory of hydrogen embrittlement of steels. Berichte Bunsenges. Phys. Chem. 1972, 76, 848–857. [Google Scholar] [CrossRef]
- Birnbaum, H.; Sofronis, P. Hydrogen-enhanced localized plasticity—A mechanism for hydrogen-related fracture. Mater. Sci. Eng. A 1994, 176, 191–202. [Google Scholar] [CrossRef]
- Yu, H.; Olsen, J.S.; He, J.; Zhang, Z. Hydrogen-microvoid interactions at continuum scale. Int. J. Hydrog. Energy 2018, 43, 10104–10128. [Google Scholar] [CrossRef]
- Zhao, K.; He, J.; Mayer, A.; Zhang, Z. Effect of hydrogen on the collective behavior of dislocations in the case of nanoindentation. Acta Mater. 2018, 148, 18–27. [Google Scholar] [CrossRef]
- Všianská, M.; Šob, M. The effect of segregated sp-impurities on grain-boundary and surface structure, magnetism and embrittlement in nickel. Prog. Mater. Sci. 2011, 56, 817–840. [Google Scholar] [CrossRef]
- Černý, M.; Šesták, P.; Řehák, P.; Všianská, M.; Šob, M. Ab initio tensile tests of grain boundaries in the fcc crystals of Ni and Co with segregated sp-impurities. Mater. Sci. Eng. A 2016, 669, 218–225. [Google Scholar] [CrossRef]
- Tahir, A.M.; Janisch, R.; Hartmaier, A. Ab initio calculation of traction separation laws for a grain boundary in molybdenum with segregated C impurites. Modell. Simul. Mater. Sci. Eng. 2013, 21, 075005. [Google Scholar] [CrossRef] [Green Version]
- Janisch, R.; Ahmed, N.; Hartmaier, A. Ab initio tensile tests of Al bulk crystals and grain boundaries: Universality of mechanical behavior. Phys. Rev. B 2010, 81, 184108. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Bean, J.J.; McKenna, K.P. Origin of differences in the excess volume of copper and nickel grain boundaries. Acta Mater. 2016, 110, 246–257. [Google Scholar] [CrossRef] [Green Version]
- Shiga, M.; Yamaguchi, M.; Kaburaki, H. Structure and energetics of clean and hydrogenated Ni surfaces and symmetrical tilt grain boundaries using the embedded-atom method. Phys. Rev. B 2003, 68, 245402. [Google Scholar] [CrossRef]
- Černý, M.; Pokluda, J. Ideal tensile strength of cubic crystals under superimposed transverse biaxial stresses from first principles. Phys. Rev. B 2010, 82, 174106. [Google Scholar] [CrossRef]
- Černý, M.; Šesták, P.; Řehák, P.; Všianská, M.; Šob, M. Atomistic approaches to cleavage of interfaces. Modell. Simul. Mater. Sci. Eng. 2019, 27, 035007. [Google Scholar] [CrossRef]
- Tran, R.; Xu, Z.; Radhakrishnan, B.; Winston, D.; Sun, W.; Persson, K.A.; Ong, S.P. Surface energies of elemental crystals. Sci. Data 2016, 3, 160080. [Google Scholar] [CrossRef] [Green Version]






| uniaxial loading | |
| uniaxial deformation | 0 |
| triaxial loading | |
| isotropic deformation | |
| isotropic loading |
| GB | Plane | Rotation | Rotation | k-Points Grid | N | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Axis | Angle | (Å) | (J/m) | (Å) | (Å) | (Å) | |||||
| 3 | present | 109.5° | 0.02 | 0.06 | 24.4 | 4.29 | 2.49 | 1 × 6 × 10 | 24 | ||
| Reference [7] | 0.05 | 0.18 | 24.5 | 4.32 | 2.50 | 1 × 6 × 10 | 24 | ||||
| Reference [26] | 0.01 | 0.04 | - | - | - | 1 × 3 × 3 | - | ||||
| Reference [11] | −0.11 | 0.09 | 24.3 | 4.73 | 4.94 | 1 × 4 × 4 | 48 | ||||
| 5 | present | 36.9° | 0.26 | 1.26 | 24.4 | 7.81 | 3.49 | 1 × 3 × 7 | 60 | ||
| Reference [7] | 0.38 | 1.29 | 16.4 | 7.93 | 3.55 | 2 × 4 × 8 | 40 | ||||
| Reference [18] | - | 1.23 | 23.6 | 7.87 | 3.52 | 2 × 6 × 18 | 60 | ||||
| Reference [26] | 0.35 | 1.23 | - | - | - | 1 × 3 × 3 | - | ||||
| Reference [11] | 0.45 | 1.30 | 22.9 | 7.82 | 6.80 | 1 × 3 × 3 | - | ||||
| 11 | present | 50.5° | 0.08 | 0.43 | 32.1 | 8.23 | 2.48 | 1 × 3 × 10 | 60 | ||
| Reference [11] | 0.06 | 0.47 | 21.7 | 8.22 | 4.93 | 1 × 4 × 4 | 80 |
| GB | Unrelaxed | Relaxed | ||
|---|---|---|---|---|
| Clean | With H | Clean | With H | |
| 3(111) | 3.78 | 2.77 | 3.76 | 2.34 |
| 5(210) | 4.00 | 3.41 | 3.59 | 1.82 |
| 11(311) | 4.35 | 3.76 | 4.15 | 3.37 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šesták, P.; Černý, M.; Zhang, Z.; Pokluda, J. Extraordinary Response of H-Charged and H-Free Coherent Grain Boundaries in Nickel to Multiaxial Loading. Crystals 2020, 10, 590. https://doi.org/10.3390/cryst10070590
Šesták P, Černý M, Zhang Z, Pokluda J. Extraordinary Response of H-Charged and H-Free Coherent Grain Boundaries in Nickel to Multiaxial Loading. Crystals. 2020; 10(7):590. https://doi.org/10.3390/cryst10070590
Chicago/Turabian StyleŠesták, Petr, Miroslav Černý, Zhiliang Zhang, and Jaroslav Pokluda. 2020. "Extraordinary Response of H-Charged and H-Free Coherent Grain Boundaries in Nickel to Multiaxial Loading" Crystals 10, no. 7: 590. https://doi.org/10.3390/cryst10070590
APA StyleŠesták, P., Černý, M., Zhang, Z., & Pokluda, J. (2020). Extraordinary Response of H-Charged and H-Free Coherent Grain Boundaries in Nickel to Multiaxial Loading. Crystals, 10(7), 590. https://doi.org/10.3390/cryst10070590