Adenine as a Halogen Bond Acceptor: A Combined Experimental and DFT Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Synthesis of the Cocrystal 1
2.3. Characterization
2.4. Computational Details
3. Results and Discussion
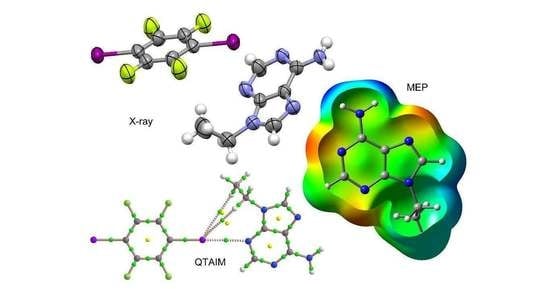
3.1. Structural Analysis
3.2. Packing Efficiency
3.3. Theoretical Study
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lehn, J.M. Supramolecular Chemistry: Concepts and Perspectives, 1th ed.; Wiley VCH: Weinheim, Germany, 1995. [Google Scholar]
- Gilli, G.; Gilli, P. The Nature of the Hydrogen Bond; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Clark, T. σ-Holes. WIREs Comput. Mol. Sci. 2013, 3, 13–20. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef] [PubMed]
- Bauza, A.; Mooibroek, T.J.; Frontera, A. The bright future of unconventional σ/π-hole interactions. ChemPhysChem 2015, 16, 2496–2517. [Google Scholar] [CrossRef]
- Crabtree, R.H. Hypervalency, secondary bonding and hydrogen bonding: Siblings under the skin. Chem. Soc. Rev. 2017, 46, 1720–1729. [Google Scholar] [CrossRef]
- Scholfield, M.R.; Vander Zanden, C.M.; Carter, M.; Ho, P.S. Halogen bonding (X-bonding): A biological perspective. Protein Sci. 2013, 22, 139–152. [Google Scholar] [CrossRef] [PubMed]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The halogen bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed]
- Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef] [Green Version]
- Hassel, O.; Hvoslef, J. The structure of Bromine 1,4-dioxanate. Acta. Chem. Scand. 1954, 8, 873. [Google Scholar] [CrossRef]
- Auffinger, P.; Hays, F.A.; Westhof, E.; Ho, P.S. Halogen bonds in biological molecules. Proc. Natl. Acad. Sci. USA 2004, 101, 16789–16794. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [Green Version]
- Voth, A.R.; Khuu, P.; Oishi, K.; Ho, P.S. Halogen bonds as orthogonal molecular interactions to hydrogen bonds. Nat. Chem. 2009, 1, 74–79. [Google Scholar] [CrossRef] [PubMed]
- Hardegger, L.A.; Kuhn, B.; Spinnler, B.; Anselm, L.; Ecabert, R.; Stihle, M.; Gsell, B.; Thoma, R.; Diez, J.; Benz, J.; Plancher, J.M.; Hartmann, G.; Banner, D.W.; Haap, W.; Diederich, F. Systematic investigation of halogen bonding in protein-ligand interactions. Angew. Chem. Int. Ed. 2011, 50, 314–318. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Xu, Z.; Shi, J.; Zhu, W.L. Underestimated halogen bonds forming with protein backbone in protein data bank. J. Chem Inf. Model. 2017, 57, 1529–1534. [Google Scholar] [CrossRef] [PubMed]
- Ho, P.S. Halogen bonding in medicinal chemistry: From observation to prediction. Future Med. Chem. 2017, 9, 637–640. [Google Scholar] [CrossRef]
- Mendez, L.; Henriquez, G.; Sirimulla, S.; Narayan, M. Looking back, looking forward at halogen bonding in drug discovery. Molecules 2017, 22, 1397. [Google Scholar] [CrossRef]
- Voth, A.R.; Hays, F.A.; Ho, P.S. Directing macromolecular conformation through halogen bonds. Proc. Natl. Acad. Sci. USA 2007, 104, 6188–6193. [Google Scholar] [CrossRef]
- Danelius, E.; Andersson, H.; Jarvoll, P.; Lood, K.; Gräfenstein, J.; Erdélyi, M. Halogen bonding: A powerful tool for modulation of peptide conformation. Biochemistry 2017, 56, 3265–3272. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Cryst. 2016, B72, 171–179. [Google Scholar] [CrossRef]
- García-Raso, A.; Fiol, J.J.; Bádenas, F.; Solans, X.; Font-Bardia, M. Reaction of trimethylene–bisadenine with d10 divalent cations. Polyhedron 1999, 18, 765–772. [Google Scholar] [CrossRef]
- Walker, N.; Stuart, D. An empirical method for correcting diffractometer data for absorption effects. Acta Crystallogr. 1983, A39, 158–166. [Google Scholar] [CrossRef]
- Farrugia, L.J. WinGX suite for small-molecule single-crystal crystallography. J. Appl. Cryst. 1999, 32, 837–838. [Google Scholar] [CrossRef]
- Burla, M.C.; Caliandro, R.; Carrozzini, B.; Cascarano, G.L.; Cuocci, C.; Giacovazzo, G.; Mallamo, M.; Mazzone, A.; Polidori, G. Crystal structure determination and refinement via SIR2014. J. Appl. Cryst. 2015, 48, 306–309. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. 2015, C71, 3–8. [Google Scholar]
- Macrae, C.F.; Bruno, I.J.; Chisholm, J.A.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Rodríguez-Monge, L.; Taylor, R.; van de Streek, J.; Wood, P.A. Mercury CSD 2.0 – new features for the visualization and investigation of crystal structures. J. Appl. Cryst. 2008, 41, 466–470. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comp. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian-basis sets for molecular calculations. I. Second row atoms, Z=11-18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations – potentials for the transition-metal atoms Sc to Hg. J. Chem. Phys. 1985, 82, 270–283. [Google Scholar] [CrossRef]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Keith, T.A. TK Gristmill Software; AIMAll: Overland Park, KS, USA, 2013. [Google Scholar]
- Montoro, T.; Tardajos, G.; Guerrero, A.; Torres, M.R.; Salgado, C.; Fernández, I.; Osío Barcina, J. σ-Hole⋯π and lone pair⋯π interactions in benzylic halides. Org. Biomol. Chem. 2015, 13, 6194–6202. [Google Scholar] [CrossRef] [PubMed]
- Naseer, M.M.; Bauzá, A.; Alnasr, H.; Jurkschat, K.; Frontera, A. Lone pair–π vs. σ-hole–π interactions in bromine head-containing oxacalix[2]arene[2]triazines. CrystEngComm 2018, 20, 3251–3257. [Google Scholar] [CrossRef]
- Kitaigorodsky, A. Molecular Crystals and Molecules; Physical Chemistry; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Spek, A.L. Structure validation in chemical crystallography. Acta Crystallogr. Sect. D: Biol. Crystallogr. 2009, 65, 148–155. [Google Scholar] [CrossRef] [Green Version]
- Pedireddi, V.R.; Ranganathan, A.; Ganesh, K.N. Cyanurate Mimics of Hydrogen-Bonding Patterns of Nucleic Bases: Crystal Structure of a 1:1 Molecular Complex of 9-Ethyladenine and N-Methylcyanuric Acid. Org. Lett. 2001, 3, 99–102. [Google Scholar] [CrossRef]
- Chaplot, S.L.; McIntyre, G.J.; Mierzejewski, A.; Pawley, G.S. The high-temperature phase of 1,2,4,5-tetra-fluoro-3,6-di-iodo-benzene and the phase transition. Acta Cryst. 1981, B37, 2210. [Google Scholar] [CrossRef]
- Oh, S.Y.; Nickels, C.W.; Garcia, F.; Jones, W.; Friščić, T. Switching between halogen- and hydrogen-bonding in stoichiometric variations of a cocrystal of a phosphine oxide. CrystEngComm 2012, 14, 6110–6114. [Google Scholar] [CrossRef]
- Taylor, C.R.; Day, G.M. Evaluating the Energetic Driving Force for Cocrystal Formation. Cryst. Growth Des. 2018, 18, 829–904. [Google Scholar] [CrossRef]
- Bader, R.F.W. A Bond Path: A Universal Indicator of Bonded Interactions. J. Phys. Chem. A 1998, 102, 7314–7323. [Google Scholar] [CrossRef]
- Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E. Topological information of the electron-density distribution in hydrogen-bonded systems. Acta Cryst. 2004, A60, s177. [Google Scholar] [CrossRef]
- Masunov, A.E.; Torres, K.; Dyakov, A.A.; Yushina, I.D.; Bartashevich, E.V. First-Principles Crystal Engineering of Nonlinear Optical Materials. II. Effect of Halogen Bonds on the Structure and Properties of Triiodobenzenes. J. Phys. Chem. C 2018, 122, 22622–22631. [Google Scholar] [CrossRef]
- Barczynski, P.; Ratajczak-Sitarz, M.; Nowaczyk, L.; Katrusiak, A.; Dega-Szafran, Z.; Komasa, A.; Szafran, M. Structure and conformation of 2, 3-diethoxycarbonyl-1-methylpyridinium iodide studied by NMR, FTIR, Raman, X-ray diffraction and DFT methods. Spectrochim. Acta, Part A: Mol. Biomol. Spectroscopy 2013, 115, 208–218. [Google Scholar] [CrossRef]






| Crystal | Cocrystal 1 |
|---|---|
| Empirical Formula | C20H18F4I2N10 |
| Mr | 728.24 |
| Crystal system | Triclinic |
| Space group | P ī |
| a/Å | 5.490(8) |
| b/Å | 8.505(5) |
| c/Å | 14.446(8) |
| α/° | 79.20(5) |
| β/° | 80.81(7) |
| γ/° | 73.29(7) |
| V/Å3 | 630.6(11) |
| Z | 1 |
| Radiation type | Mo Kα |
| μ/ mm−1 | 2.554 |
| Temperature/K | 294(2) |
| Crystal size/ mm | 0.360 × 0.270 × 0.180 |
| Dcalc/ g·cm−3 | 1.918 |
| Reflections collected | 2320 |
| Independent Reflections | 2208 [R(int) = 0.0548] |
| Completeness to theta = 24.996° | 99.5 % |
| F(000) | 350 |
| Data/ restraints/ parameters | 2202/0/164 |
| Goodness-of-fit | 1.100 |
| Final R indices [I < 2d(I)] | R1 = 0.0507, wR2 = 0.1383 |
| R indices (all data) | R1 = 0.0738, wR2 = 0.1493 |
| Largest diff. peak and hole/ e·Å−3 | 0.728 and −0.701 |
| CCDC number | 1903339 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roselló, Y.; Benito, M.; Molins, E.; Barceló-Oliver, M.; Frontera, A. Adenine as a Halogen Bond Acceptor: A Combined Experimental and DFT Study. Crystals 2019, 9, 224. https://doi.org/10.3390/cryst9040224
Roselló Y, Benito M, Molins E, Barceló-Oliver M, Frontera A. Adenine as a Halogen Bond Acceptor: A Combined Experimental and DFT Study. Crystals. 2019; 9(4):224. https://doi.org/10.3390/cryst9040224
Chicago/Turabian StyleRoselló, Yannick, Mónica Benito, Elies Molins, Miquel Barceló-Oliver, and Antonio Frontera. 2019. "Adenine as a Halogen Bond Acceptor: A Combined Experimental and DFT Study" Crystals 9, no. 4: 224. https://doi.org/10.3390/cryst9040224
APA StyleRoselló, Y., Benito, M., Molins, E., Barceló-Oliver, M., & Frontera, A. (2019). Adenine as a Halogen Bond Acceptor: A Combined Experimental and DFT Study. Crystals, 9(4), 224. https://doi.org/10.3390/cryst9040224