Insight into the Optoelectronic and Thermoelectric Properties of Mn Doped ZnTe from First Principles Calculation
Abstract
:1. Introduction
2. DFT Calculation Technique
3. Results and Discussion
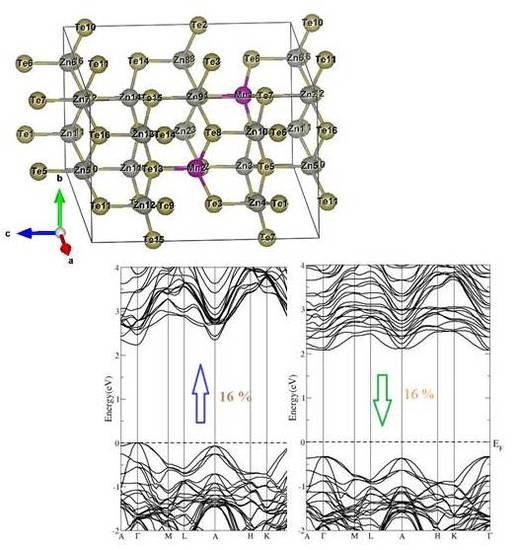
3.1. Electronic Structure
3.2. Optical Function Dispersion
3.3. Thermoelectric Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mingo, N. Thermoelectric figure of merit of II-VI semiconductor nanowires. Appl. Phys. Lett. 2004, 85, 5986. [Google Scholar] [CrossRef]
- Ghosh, B.; Ghosh, D.; Hussain, S.; Bhar, R.; Pal, A.K. Growth of ZnTe films by pulsed laser deposition technique. J. Alloys Compd. 2012, 541, 104–110. [Google Scholar] [CrossRef]
- Ko, H.; Park, S.; An, S.; Lee, C. Intense near-infrared emission from undoped ZnTe nanostructures synthesized by thermal evaporation. J. Alloys Compd. 2013, 580, 316–320. [Google Scholar] [CrossRef]
- Yang, X.H. Enhancing thermoelectric properties of semiconductors by heavily doping isoelectronic elements with electronegativities distinct from the host atoms. J. Alloys Compd. 2014, 594, 70–75. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, B.G. Ferromagnetism in transition-metal-doped II-VI compounds. J. Magn. Magn. Mater. 2006, 307, 245–249. [Google Scholar] [CrossRef]
- Guo, M.; Gao, G.; Hu, Y. Magnetism and electronic structure of Mn- and V-doped zinc blende ZnTe from first-principles calculations. J. Magn. Magn. Mater. 2011, 323, 122–126. [Google Scholar] [CrossRef]
- Saito, H.; Zayets, V.; Yamagata, S.; Ando, K. Room-Temperature Ferromagnetism in a II-VI Diluted Magnetic Semiconductor ZN1-CrxTe. Phys. Rev. Lett. 2003, 90, 207202. [Google Scholar] [CrossRef]
- Reddy, D.R.; Reddy, B.K. Laser-like mechanoluminescence in ZnMeTe-diluted magnetic semiconductor. Appl. Phys. Lett. 2002, 81, 460–462. [Google Scholar] [CrossRef]
- Imamura, M.; Okada, A. Magnetooptical Properties of ZnMeTe Films Grown on Sapphire Substrates. IEEE Trans. Magn. 2006, 42, 3078–3080. [Google Scholar] [CrossRef]
- Kulatov, E.; Uspenskii, Y.; Mariette, H.; Cilbert, J.; Ferrand, D.; Nakayama, H.; Ohta, H. Ab Initio study of Magnetism in III-V- and II-VI-Based Diluted Magnetic Semiconductors. J. Supercond. Nov. Magn. 2003, 16, 123–126. [Google Scholar] [CrossRef]
- Cheng, J.; Li, D.; Cheng, T.; Ren, B.; Wang, G.; Li, J. Aqueous synthesis of high-fluorescence ZdZnTe alloyed quantum dots. J. Alloys Compd. 2014, 589, 539–544. [Google Scholar] [CrossRef]
- Sandratskii, L.M.; Bruno, P. Density functional theory of high-TC ferromagnetism of (ZnCr)Te. J. Phys. Condens. Matter. 2003, 15, 585–590. [Google Scholar] [CrossRef]
- Wang, X.L.; Dou, S.X.; Zhang, C. Zero-gap materials for future spintronics, electronics and optics. NPG Asia Mater. 2010, 2, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Shan, C.X.; Fan, X.W.; Zhang, J.Y.; Zhang, Z.Z.; Wang, X.H.; Ma, J.G.; Lu, Y.M.; Liu, Y.C.; Shen, D.Z.; Kong, X.G.; et al. Structural and luminescent properties of ZnTe film grown on silicon by metalorganic chemical vapor deposition. J. Vac. Sci. Technol. A 2002, 20, 1886–1890. [Google Scholar] [CrossRef]
- Rao, G.K.; Bangera, K.V.; Shivakumar, G.K. Studies on the photoconductivity of vacuum deposited ZnTe thin films. Mater. Res. Bull. 2010, 45, 1357–1360. [Google Scholar] [CrossRef]
- Raju, K.N.; Vijayalakshmi, R.P.; Venugopal, R.; Reddy, D.R.; Reddy, B.K. Effect of substrate temperature on the structural, optical and electrical properties of vacuum-evaporated ZnTe films. Mater. Lett. 1992, 13, 336–341. [Google Scholar] [CrossRef]
- Su, C.H.; Volz, M.P.; Gillies, D.C.; Szofran, F.R.; Lehoczky, S.L.; Dudley, M.; Yao, G.D.; Zhou, W. Growth of ZnTe by physical vapor transport and traveling heater method. J. Cryst. Growth 1993, 128, 627–632. [Google Scholar] [CrossRef]
- Khan, M.R.H. Interface properties of a CdTe-ZnTe heterojunction. J. Phys. D Appl. Phys. 1994, 27, 2190–2193. [Google Scholar] [CrossRef]
- Tao, I.W.; Jurkovic, M.; Wang, W.I. Doping of ZnTe by molecular beam epitaxy. Appl. Phys. Lett. 1994, 64, 1848. [Google Scholar] [CrossRef]
- Maiti, B.; Gupta, P.; Chaudhuri, S.; Pal, A.K. Grain boundary effect in polycrystalline ZnTe films. Thin Solid Films 1994, 239, 104–111. [Google Scholar] [CrossRef]
- Wolf, K.; Stanzl, H.; Naumov, A.; Wagner, H.P.; Kuhn, W.; Hahn, B.; Gebhardt, W. Growth and doping of ZnTe and ZnSe epilayers with metalorganic vapour phase epitaxy. J. Cryst. Growth 1994, 138, 412–417. [Google Scholar] [CrossRef]
- Neumann-Spallart, M.; Konigstein, C. Electrodeposition of zinc telluride. Thin Solid Films 1995, 265, 33–39. [Google Scholar] [CrossRef]
- Bozzini, B.; Lenardi, C.; Lovergine, N. Electrodeposition ofstoichiometric polycrystalline ZnTe on n+-GaAs and Ni-P. Mater. Chem. Phys. 2000, 66, 219–228. [Google Scholar] [CrossRef]
- Jun, Y.; Kim, K.J.; Kim, D. Electrochemical synthesis of cu-doped znte films as back contacts to cdte solar cells. Met. Mater. 1999, 5, 279–285. [Google Scholar] [CrossRef]
- Arico, A.S.; Silvestro, D.; Antonucci, P.L.; Giordano, N.; Antonucci, V. Electrodeposited Thin Film ZnTe Semiconductors for Photovoltaic Applications. Adv. Perform. Mater. 1997, 4, 115–125. [Google Scholar] [CrossRef]
- Karazhanov, S.Z.; Ravindran, P.; Kjekshus, A.; Fjellvag, H.; Svensson, B.G. Electronic structure and optical properties of Zn X (X = O, S, Se, Te): A density functional study. Phys. Rev. B 2007, 75, 155104. [Google Scholar] [CrossRef]
- Huang, M.Z.; Ching, W.Y. Calculation of optical excitations in cube semiconductors. I. Electronic structure and linear response. Phys. Rev. B 1993, 47, 9449. [Google Scholar] [CrossRef]
- Subhan, F.; Azam, S.; Khan, G.; Irfan, M.; Muhammad, S.; Al-Sehemi, A.G.; Naqib, S.H.; Khenata, R.; Khan, S.; Kityk, I.V.; et al. Elastic and optoelectronic properties of CaTa2O6 compounds: Cubic and orthorhombic phases. J. Alloys Compd. 2019, 785, 232–239. [Google Scholar] [CrossRef]
- Kityk, I.V. IR-induced Second Harmonic Generation in Sb2Te3-BaF2-PbCl2 Glasses. J. Phys. Chem. B 2003, 107, 10083–10087. [Google Scholar] [CrossRef]
- Kityk, I.V. IR-stimulated second harmonic generation in Sb2Te2Se-BaF2-PbCl2 glasses. J. Mod. Opt. 2004, 51, 1179–1189. [Google Scholar]
- Shpotyuk, O.I.; Kityk, I.V.; Kasperczyk, J. Mechanism of reversible photoinduced optical effects in amorphous As2S3. J. Non Cryst. Solids 1997, 215, 218–225. [Google Scholar] [CrossRef]
















© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, W.; Azam, S.; Ullah, I.; Rani, M.; Younus, A.; Irfan, M.; Czaja, P.; Kityk, I.V. Insight into the Optoelectronic and Thermoelectric Properties of Mn Doped ZnTe from First Principles Calculation. Crystals 2019, 9, 247. https://doi.org/10.3390/cryst9050247
Khan W, Azam S, Ullah I, Rani M, Younus A, Irfan M, Czaja P, Kityk IV. Insight into the Optoelectronic and Thermoelectric Properties of Mn Doped ZnTe from First Principles Calculation. Crystals. 2019; 9(5):247. https://doi.org/10.3390/cryst9050247
Chicago/Turabian StyleKhan, Wilayat, Sikander Azam, Inam Ullah, Malika Rani, Ayesha Younus, Muhammad Irfan, Paweł Czaja, and Iwan V. Kityk. 2019. "Insight into the Optoelectronic and Thermoelectric Properties of Mn Doped ZnTe from First Principles Calculation" Crystals 9, no. 5: 247. https://doi.org/10.3390/cryst9050247
APA StyleKhan, W., Azam, S., Ullah, I., Rani, M., Younus, A., Irfan, M., Czaja, P., & Kityk, I. V. (2019). Insight into the Optoelectronic and Thermoelectric Properties of Mn Doped ZnTe from First Principles Calculation. Crystals, 9(5), 247. https://doi.org/10.3390/cryst9050247