Quest for Compounds at the Verge of Charge Transfer Instabilities: The Case of Silver(II) Chloride ^†

Abstract

Electron-transfer processes constitute one important limiting factor governing stability of solids. One classical case is that of CuI₂, which has never been prepared at ambient pressure conditions due to feasibility of charge transfer between metal and nonmetal (CuI₂ → CuI + ½ I₂). Sometimes, redox instabilities involve two metal centers, e.g., AgO is not an oxide of divalent silver but rather silver(I) dioxoargentate(III), Ag(I)[Ag(III)O₂]. Here, we look at the particularly interesting case of a hypothetical AgCl₂ where both types of redox instabilities operate simultaneously. Since standard redox potential of the Ag(II)/Ag(I) redox pair reaches some 2 V versus Normal Hydrogen Electrode (NHE), it might be expected that Ag(II) would oxidize Cl⁻ anion with great ease (standard redox potential of the ½ Cl₂/Cl⁻ pair is + 1.36 V versus Normal Hydrogen Electrode). However, ionic Ag(II)Cl₂ benefits from long-distance electrostatic stabilization to a much larger degree than Ag(I)Cl + ½ Cl₂, which affects relative stability. Moreover, Ag(II) may disproportionate in its chloride, just like it does in an oxide; this is what AuCl₂ does, its formula corresponding in fact to Au(I)[Au(III)Cl₄]. Formation of polychloride substructure, as for organic derivatives of Cl₃⁻ anion, is yet another possibility. All that creates a very complicated potential energy surface with a few chemically distinct minima i.e., diverse polymorphic forms present. Here, results of our theoretical study for AgCl₂ will be presented including outcome of evolutionary algorithm structure prediction method, and the chemical identity of the most stable form will be uncovered together with its presumed magnetic properties. Contrary to previous rough estimates suggesting substantial instability of AgCl₂, we find that AgCl₂ is only slightly metastable (by 52 meV per formula unit) with respect to the known AgCl and ½ Cl₂, stable with respect to elements, and simultaneously dynamically (i.e., phonon) stable. Thus, our results point out to conceivable existence of AgCl₂ which should be targeted via non-equilibrium approaches.

1. Introduction

Electron-transfer processes constitute one important limiting factor governing stability of solids. One classic case is that of CuI₂, which has never been prepared at ambient pressure conditions due to feasibility of charge transfer between metal and nonmetal. The energy of ligand-to-metal-charge transfer (LMCT) is negative for CuI₂ which results in instability and phase separation, according to the Equation (1):

CuI₂ → CuI + ½ I₂

(1)

While the process of oxidation of iodide anions by Cu(II) is well-known to every chemistry freshman, it remains somewhat difficult to explain to a comprehensive school pupil, based on the values of standard redox potentials, E⁰, for the relevant species in aqueous solutions. The reason for that is that the E⁰ value for the Cu(II)/Cu(I) redox pair is + 0.16 V versus NHE (Normal Hydrogen Electrode), while that for the I₂/2 I⁻ is + 0.54 V, i.e., I₂ is formally a slightly better stronger oxidizer than Cu(II). The detailed explanation necessitates departure from the aqueous conditions (note, E⁰ values are the feature of solvated species in aqueous solutions). Since Cu(II) in aqueous solutions is very strongly solvated by water molecules acting as a Lewis base (H₂O → Cu(II)), and this effect surpassed the one of coordination of water molecules to Cu(I), the oxidizing properties of naked Cu(II) are certainly stronger than those of solvated ions. Simultaneously, since I⁻ anion is coordinated by water molecules acting like Lewis acid (OH₂…I⁻) (and coordination to anion is stronger than to neutral I₂ molecules) the E⁰ value for the I₂/2 I⁻ redox pair is actually larger than the one for unsolvated species. This helps to explain why the balance of a redox reaction for the phases in the solid state, i.e., lacking any solvent, is different from the one which might be guessed based on the plain E⁰ values.

Attempts to more quantitatively explain the lack of stability of CuI₂ at ambient (p,T) conditions involve discussions of ionization potential of monovalent metal, ionic polarizabilities, as well as lattice energies of relevant solids. Over 60 years ago, following early considerations by Fajans [1], Morris estimated the standard molar free energy of formation of CuI₂ [2]. The obtained value was slightly positive, some 1 kcal/mole [2], see also [3]. Since the respective value for CuI is large and negative (circa −16.6 kcal/mole), it is natural that formation of CuI₂ is strongly disfavored. This, of course, may change under high pressure conditions, which—due to beneficial pV factor allowing to crowd cations and anions together in the lattice—often favor formation of species at high oxidation states.

Sometimes redox instabilities involve two metal centers rather than metal and nonmetal, e.g., AgO is not an oxide of divalent silver but rather silver(I) dioxoargentate(III), Ag(I)[Ag(III)O₂] [4,5]:

2 Ag(II) → Ag(I) + Ag(III)

(2)

The analogous behavior has been theoretically predicted for AuO, as well [6]. It is important to notice that the disproportionation reactions of this type are always energy uphill in the gas phase, and they are relatively rare for extended solids. In the case of silver, the energy of reaction proceeding according to Equation (2) is positive and very large, some 13.3 eV, as may be estimated from relevant ionization potentials (this value corresponds to the Mott-Hubbard U energy in the gas phase). The fact that the process takes place in AgO according to Equation (2) is given by several important factors, such as departure from ionic formulation, and the fact that U is strongly screened in solids. The rule of a thumb is that disproportionation processes are facile (i) in a Lewis-basic environment, (ii) especially when there is strong mixing of metal and nonmetal states i.e., pronounced covalence of chemical bonding, (iii) when the pV factor at elevated pressure, which prefers packing of unequal spheres, dominates the energetic terms, and (iv) at low temperatures [7]. AgO is in fact a nice exemplification of condition (i), since it is disproportionated, while its more Lewis acidic derivative, AgSO₄, is not [8]. Another good example is that of Au(II)(SbF₆)₂, which is, comproportionated, a genuine Au(II) compound [9], while its parent basic fluoride, AuF₂, has never been prepared in the solid phase, as it is subject to phase separation via disproportionation to Au and AuF₃. Moreover, AgO exemplifies condition (ii), since the chemical bonding between Ag and O is remarkably covalent in this compound, which leads to a phonon-driven disproportionation [10]. Finally, AgO, also exemplifies condition (iii), since it remains disproportionated to a pressure of at least 1 mln atm [11].

Here, we look at the particularly interesting case of an elusive AgCl₂ where, as we will see, both types of redox instabilities may happen. Since the standard redox potential of the Ag(II)/Ag(I) redox pair reaches some +2.0 V versus NHE and the respective value for the ½ Cl₂/Cl⁻ pair is +1.36 V, it might naturally be expected that Ag(II) would oxidize Cl⁻ anion with great ease (the above-mentioned arguments valid for CuI₂ are also valid for AgCl₂). However, ionic Ag(II)Cl₂ benefits from long-distance electrostatic stabilization to a much larger degree than Ag(I)Cl + ½ Cl₂, which should affect relative stability. Moreover, since the Ag(II)–Cl bonding is naturally expected to be quite covalent, similarly to the Ag(II)–O one in AgO (Cl and O have nearly identical electronegativities), Ag(II) might disproportionate in its chloride, just like it does in oxide. This is in fact what related AuCl₂ does, its true formula corresponding in fact to Au(I)[Au(III)Cl₄] [12]. Formation of polychloride substructure, as for organic derivatives of Cl₃⁻ anion [13,14], or a mixed chloride-polychloride (Ag(I)₂(Cl)(Cl₃)), is yet another possibility. Last but not the least, AgCl₂ featuring an unpaired electron at the transition metal center may choose to form exotic Ag–Ag bond, as is observed for AuSO₄ [15]. All that creates a complicated potential energy surface with a few chemically distinct minima, i.e., diverse polymorphic forms present, and this renders theoretical predictions troublesome.

The major aim of this work is to theoretically predict crystal structure, stability, and presumed electronic and magnetic properties of the most stable form of AgCl₂. We would like also to computationally verify early predictions by Morris who estimated the free enthalpy of reaction:

AgCl₂ → AgCl and ½ Cl₂

(3)

to be strongly negative, some −96.4 kJ/mole [2]. Finally, we will briefly discuss the anticipated impact of elevated pressure on the course of the reaction described by Equation (3), as well as magnetic properties of the most stable phases found.

2. Methodology

This study has begun in resemblance with our previous theoretical search for AgSO₄, where we have employed the method of following imaginary phonon modes to reach dynamically stable structural models [16,17]. Using this method, we have optimized the hypothetical AgCl₂ crystal in all known crystal structure polytypes taken by metal dihalides, MX₂ (X = F, Cl, Br, I) (i.e., over 40 structure types) using the plane-wave code VASP (Vienna Ab-initio Simulation Package) [18,19,20,21,22], and subsequently calculated phonon dispersion curves for each model using the program PHONON [23]. In cases where at least one imaginary phonon was detected (signaling dynamic instability), we followed the normal coordinate of this mode to reach another, lower symmetry and lower energy structure [17,24], and we reexamined phonons after optimization. Due to complexity and CPU burden of the task this preliminary quest was conducted with LDA functional and lower plane-wave cut-off equal to 400 eV. In the second approach, the evolutionary algorithm approach was applied using XtalOpt [25,26,27,28] in combination with VASP and using GGA (general gradient approximation) with Perdew-Burke-Ernzerhof functional adapted for solids (PBEsol) and plane-wave cutoffs of 520 eV. Using the evolutionary algorithms, we have considered unit cells containing 2, 4, and 8 formula units and generated a pool of 2183 structures. The lowest energy structures originating from both methods were ultimately recalculated with spin-polarization, on-site Coulomb interactions and van der Waals corrections, as outlined below. Magnetic models were constructed for polymorphic forms containing genuine Ag(II) paramagnetic centers and the lowest energy spin arrangements were found using the rotationally invariant density functional theory DFT + U method introduced by Liechtenstein et al. where the values of both Hubbard U and the Hund J parameter are set explicitly [29]. The U and J parameters were set only for d orbitals of the Ag atoms and the values of 5 eV and 1 eV were used, respectively [30]. The van der Waals interactions were accounted for using the DFT-D3 correction method of Grimme et al. with Becke-Jonson damping [31]. Additionally, the hybrid DFT calculations with HSE06 functional were used to calculate the mixed-valence Ag^IAg^IIICl₂ solution that could not be properly stabilized at the DFT level.

Electronic density of states was calculated using the aforementioned DFT + U method with DFT-D3 van der Waals correction, with k-mesh of 0.025 Å⁻¹ and 800 eV plane-wave cutoff. The disproportionated AgCl₂ and AuCl₂ structures were additionally pre-optimized with HSE06 functional using a coarser k-mesh of 0.05 Å⁻¹.

3. Results

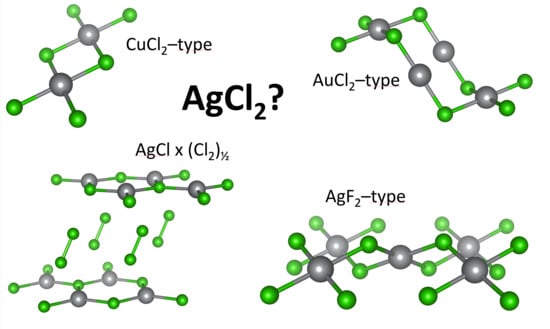
3.1. Scrutiny of Dynamically Stable Polymorphic forms of AgCl₂ (Method of Following Imaginary Phonon Modes)

The crystal structures selected for preliminary study accounted for numerous polytypes known among the transition metal and alkali earth metal dihalides. Both more ionic as well as more covalent structural types were tested. AgF₂, AuCl₂, CuCl₂, PdF₂, PtCl₂, PbCl₂ (cottunite), α–PbO₂, and TiO₂ (rutile) were selected because of obvious structural analogies within Group 11 of the Periodic Table of Elements, or because they are often adopted by metal chlorides [24]. Among those, KAuF₄ and AuCl₂ types with K or Au atoms substituted by Ag ones, represent disproportionated Ag(I)/Ag(III) systems; others correspond to comproportionated ones. We have also employed a set of ionic halide structures, notably: CaF₂ (fluorite), CaCl₂ (Pmn2₁ and Pnnm polytypes), CdCl₂, layered CdI₂, MgCl2 (P4m2, Ama2 and P–1 polymorphs), SrI₂, YbCl₂, as well as polymeric BeF₂, and three covalent structures: SiS₂, FeP₂, and XeF₂. Altogether, these representative prototypes show a rich variety of structural motifs and lattice dimensionalities. Using the method of following the imaginary modes of AgCl₂ in these types of structures we have obtained over 10 dynamically stable structures. Figure 1a–f illustrates the six main structural motives present in them. All remaining predicted polymorphs are simply various polytypes of these (differ in stacking of the main structural motives).

The main structural building block in all dynamically stable models is a [AgCl₄] plaquette. Here, silver is stabilized in a close to square-planar (or elongated octahedral) coordination by chloride anions, which is the most common coordination sphere of Ag^II cation among the known compounds [32]. Silver in the second oxidation state is seldom found in a linear (or a contracted octahedral) coordination, and other geometries are even more scarce. This behavior is nicely reflected by the results of our extensive structure screening. For example, the compressed octahedral coordination appeared in our search only once in a rutile type structure. Although predicted to be dynamically stable at DFT level, it was ruled out in the subsequent spin-polarized DFT + U calculations, where it converged to a square-planar coordination. The 2 + 4 coordination is indeed more common for fluorides in rutile structure (PdF₂ and NiF₂), but no such chloride is known. In one case, a butterfly penta-coordination (i.e., close to a tetragonal pyramide) was obtained, where the silver atoms are displaced out of the plain formed by the [AgCl₄] plaquettes (Figure 1f). Such geometry has been previously observed for Ag^II in two high-pressure polymorphs of AgF₂: a layered and a tubular one [33]. In both, the silver atoms depart from the center of the ideally flat square-planar [AgF₄] units to achieve batter packing while simultaneously preserving the local Jahn−Teller distortion. The AgCl₂ structure with the butterfly silver coordination is topologically equivalent to the layered HP1 polymorph of AgF₂. Indeed, it exhibits the lowest calculated volume among the predicted dynamically stable structures and thus it should be stabilized at high pressure (see section 3). Our scrutiny of AgCl₂ polytypes provides theoretical evidence that the butterfly coordination is indeed a natural response of octahedral Ag^II sites (4 + 2 coordination) to high pressures and it permits more effective packing of 4 + 1 + 1 distorted [Ag^IIX₆] units.

The [Ag^IIX₄] squares show three distinct connectivity patterns in the dynamically stable polymorphs. They are connected either by corners, edges or via a combination of the two, while the resulting lattice is one- or two-dimensional at most. This comes as no surprise since it is natural for the strongly Jahn-Teller active cation to exhibit reduced structural dimensionality in its compounds. Here, the edge sharing always results in one-dimensional chains that have a shape of infinite molecular ribbons (Figure 1a). On the other hand, corner and combined corner plus edge sharing leads always to layered structures (Figure 1b–f). No polymorphs with isolated [AgCl₄] units or three-dimensional connectivity were found. Additionally, it may be noticed that each chlorine atom is always shared between two Ag cations thus AgCl₂ strictly avoids chlorine terminals in its structures. This, too, is quite natural, since Ag^II is an electron deficient and Lewis acidic cation, which attempts to satisfy its need for electronic density by having at least four anions in its coordination sphere; at AgCl₂ stoichiometry this implies ligand sharing, i.e., [AgCl_4/2]. The charge depletion on Cl atoms affects the halogen-halogen interactions, as discussed in Supplementary Materials (S1).

Structures with infinite ribbons are characteristic of dihalides containing Jahn-Teller active cations and are also present in cuprates such as LiCu₂O₂ [34] and LiCuVO₄ [35]. In halides, the ribbons have neutral charge and these structures are held together by van der Waals interactions. In the cuprates, the ribbons are present as anionic species [CuO₂]²⁻_∞, whose charge is compensated by the presence of additional metal cations. Although observed in majority of halides containing Jahn-Teller ions including CuCl₂, CuBr₂, PdCl₂, PtCl₂, and CrCl₂, they have never been observed in compounds of silver. Importantly, for AgCl₂ this structure polytype has the lowest computed energy as will be discussed later in the text.

Three district structural patterns are observed among the layered polymorphs. In the first case, fragments of the ribbons may be distinguished that consist of two [AgCl₄] units sharing one edge. These [Ag₂Cl₆] dimers then interconnect into layers by sharing corners (Figure 1b). Another structural pattern is formed by alternation of the same dimmers with single squares (Figure 1c). The third type of layers is formed by squares sharing only corners (Figure 1d–f). The layered polymorphs containing the dimeric units are unique among the halides. They are closely related to orthorhombic ramsdellite [36] and monoclinic γ-MnO₂ polymorph form [37]. The ramsdellite structure consists of three-dimensional network of double chains of edge-sharing MnO₆ octahedra while in the γ-MnO₂ the double chains alternate with single chains of MnO₆ octahedra (Figure 2a,b). In the predicted AgCl₂ polymorphs with the dimeric [Ag₂Cl₆] units (Figure 1b), the three-dimensional network of the ramsdellite structure is reduced to two-dimensional one due to Jahn-Teller distortion of the octahedra that takes place in the direction parallel to the propagation of the chains. The same relation exists between the AgCl₂ polymorph formed by alternation of the [Ag₂Cl₆] dimers with [AgCl₄] squares (figure 1c) and the γ-MnO₂ structure. Although no such halides exist, the ramsdellite-related AgCl₂ structure has its zero-dimensional analogues in 4d and 5d transition metal pentachlorides such as MoCl₅, Ta₂Cl₁₀, NbCl₅, WCl₅. They consist of dimeric M₂Cl₁₀ units of edge-sharing MCl₆ octahedra aligned into infinite chains (Figure 2c). One can imagine obtaining the ramsdellite and the related layered AgCl₂ structure by virtual polymerization of the M₂Cl₁₀ dimmers and subsequent Jahn-Teller distortion, respectively. While the layered structure containing the dimeric [M₂Cl₆] units are to best of our knowledge unknown, the layers with corner-sharing of square planar [MCl₄] units are well documented for transition metal halides including CuF₂, AgF₂, or PdCl₂; thus, it is quite natural to detect them for related AgCl₂.

All polymorphs predicted in this study are related to three archetypical structures, namely CdI₂, rutile, and fluorite structure. All ribbon polymorphs may be derived from the layered CdI₂ prototype, where each layer is formed by edge-sharing [CdI₆] octahedra. Replacing the octahedral cadmium cation by a Jahn-Teller active one leads to elongation of octahedra and dissociation of the layers into infinite ribbons as illustrated in Figure 3c. In fact, the CdI₂-type layers and ribbons are the most common structural motives among transition metal dihalides. Notably, all dichlorides of 3d elements crystallize in the CdI₂ polytypes, the only exception being those containing Jahn-Teller active ions, which in turn crystallize in ribbon structures.

The layered polymorphs containing the [Ag₂Cl₆] dimers can be also derived from the CdI₂ structure. As already emphasized, the ribbon structure may be obtained from the CdI₂ structure simply by elongation of the [CdI₆] octahedra. This elongation is a consequence of Jahn-Teller stabilization (expansion) of the dz² orbitals, which may in principle be realized along any of the three main octahedral axes denoted by letters A, B and C in Figure 3b. This gives way to various possible orbital ordering patterns and thus various types of connectivity of the [AgCl₄] plaquettes. While the same orientation of the dz² orbitals along the A direction (ferrodistortive AAA orbital ordering pattern) leads to the ribbon polymorphs, alternating orientation of the orbitals (antiferrodistortive ordering patterns) results in layered polymorphs featuring corner-shared [Ag₂Cl₆] dimers. Here, the Jahn-Teller distortion takes place alternatively along the B and C direction while two such orbital ordering patterns are possible. The AACAAC orbital ordering pattern leads to a layer containing monomeric and dimeric units (Figure 1c and Figure 3d) and AACC pattern to a layer containing only dimeric units (Figure 1b and Figure 3e).

CdI₂ structure allows also for derivation of the layers with corner-sharing plaquettes, which may be achieved by ACAC ordering pattern and is in fact observed in low-temperature γ-PdCl₂ (Figure 1d, bottom) [38]. However, the predicted layered polymorphs of AgCl₂ with corner-sharing no longer belong to the CdI₂ family but rather to rutile and fluorite family as manifested by change of the axial coordination of the Ag atoms from intralayer to interlayer one (Figure 1d–e). Note that in all the ribbon and layered polymorphs derived from the CdI₂ structure, the cations are always octahedrally coordinated by intralayer anions; that is, by anions belonging to the same CdI₂-type layer. On the other hand, the silver atoms from the corner-shared AgCl₂ layers complete their octahedral coordination by axial chlorine atoms from adjacent layers (Figure 1). To do so, the CdI₂ layers must become less corrugated. Such geometrical arrangements are characteristic of a rutile structure. This prototypical structure consists of three-dimensional network of corner- and edge-shared octahedra. Orbital ordering at Jahn-Teller active cations in these octahedra may result in formation of layers consisting of corner-shared plaquettes, where each metal cation from each plaquette is axially coordinated by anions from adjacent layers, as exemplified by CuF₂ structure (Figure 4b). Furthermore, various stacking patterns of these layers may be realized. The simplest AA stacking is stabilized in the monoclinic CuF₂ type and the ABAB stacking in the orthorhombic AgF₂ type. Yet another structure with AB’AB’ stacking was found that differs from the AgF₂ type by smaller relative shift of the layers (an intermediate between CuF₂ and AgF₂ structure) (Figure 5). These various stacking patters result in different axial contacts of the cations and diverse packing efficiencies. Recall that CuF₂ is rutile type structure. On the other hand, the AgF₂ structure is related to fluorite structure, where the cations reach for two additional ligands to complete a cubic coordination [11]. Compounds with rutile-like structures often transform to denser fluorite-like structure under pressure. Thus, three distinct stable layered forms of AgCl₂-CuF₂ type, AgF₂ type, and intermediate between the two with different stacking of the layers, might be achieved under different pressure conditions. More on that later.

Similarly, as in the case of the layered structures, several polytypes were found for the ribbon structures. While the AgCl₂ ribbons maintain the layered organization of the CdI₂ prototype with the interlayer contacts being longer than the intralayer ones, stacking of these layers may vary (Figure 6). We have obtained various polytypes in our search using evolutionary algorithms. The simplest stacking corresponds to one layer per unit cell that directly relates to the CdI₂ type structure. The original trigonal P-3m symmetry of the CdI₂ type is however lowered to triclinic due to the presence of the Jahn-Teller active Ag^II cation. Additionally, a monoclinic C2m structure of copper dihalide type was found in our scrutiny, as well as an orthorhombic and a triclinic version of the PdCl₂ polymorphs (Figure 6). Note, PdCl₂ crystallizes in two ribbon-like structures, a high-temperature orthorhombic and a low-temperature monoclinic form, which differ only in the monoclinic angle. Our results provide theoretical support for the observed strong tendency of the late TM dihalides with Jahn-Teller cations to form ribbon-like crystal structures exhibiting various packing.

Note that both rutile and fluorite structures are prototype structures for ionic crystals, while the CdI₂ structure is preferred by compounds forming more covalent bonds. In the predicted polymorphs of AgCl₂, we see frequent realization of structures related to both more ionic as well as more covalent structural types. This may be a manifestation of the intermediate character of the chemical bonding in AgCl₂.

3.2. The Unusual Ag(I)Cl(Cl₂)_½ Polymorph

As explained in the introduction, one of the key difficulties in preparation of the Ag(II) dichloride from elements or from AgCl and excess of Cl₂ is related to the fact that Ag(II) is a potent oxidizer. This means that silver might prefer to adopt its most common monovalent state (as AgCl), while the excess Cl atom would be forced to form Cl–Cl bonds with other similar species around. On the other hand, the so-formed Cl₂ is known to interact with Cl⁻ anions in ionic compounds, by forming an asymmetric [Cl⁻…Cl₂] or even symmetric [Cl-Cl-Cl⁻] [39,40,41] trichloride anion. While the propensity of Cl₃⁻ to form is much smaller than that of the related triiodide anion, yet such a Lewis structure should not escape our attention. Indeed, the XTalOpt quest has yielded one structure with the Ag(I)[Cl(Cl₂)_½] formulation (Figure 7). It consists of AgCl double layers with Cl₂ molecules sandwiched in between them.

The structures of Ag(I)[Cl(Cl₂)_½] consist of the AgCl layers which can form either rock-salt layers or pseudo-hexagonal ones with only three short Ag-Cl bonds (Figure 7). The appearance of the rock salt layers seems natural since AgCl in rock salt structure is well known. However, the hexagonal layers are unknown among plain Ag(I) halides, with AgX (X = F, Cl, Br, I) adopting an ionic NaCl polytype (CN = 6), while AgI additionally takes on several structures with tetrahedral coordination of cation (CN = 4) (i.e., wurtzite, sphalerite, SiC(4H), etc.). In addition, CN of 7 is also possible for AgCl at rather low pressure of circa 1 GPa (TiI polytype [42]). The very low CN of 3 for Ag(I) in pseudo-hexagonal BN-like layer and a very short bond length of 2.521 Å indicates more covalent in respect the rock salt structure (six bonds at 2.773 Å [42]). Since the intra-sheet Ag-Cl bonding is covalent, it is not surprising to see that the interactions of Cl₂ with Cl⁻ anions are far from symmetric, with intra-molecular Cl-Cl bond of 2.054 Å (slightly longer than that found for molecular solid of Cl₂, 1.97 Å), and Cl…Cl⁻ separation of 2.874 Å. That the Cl-Cl bond length is slightly longer than for free Cl₂ obviously stems from the donor-acceptor character of the Cl⁻…Cl₂ interactions, and slight occupation of the sigma* orbital of Cl₂.

Formation of AgCl intercalated with Cl₂ molecules is peculiar given substantial lattice energy of AgCl solid, and little energy penalty to break weak Cl⁻…Cl₂ interactions upon phase separation to AgCl and ½ Cl₂. Their appearance in our quest is probably related to the limit imposed to Xtalopt on number of formula units and it marks the tendency towards the phase separation. We will turn to stability of these structures in the next section and discuss pressure effects further on.

3.3. Relative and Absolute Energetic and Thermodynamic Stability of Several Important Polymorphic Forms of AgCl₂

The crystal structures of all polymorphs considered here has been provided as cif files in Supplementary Materials (S2).

At DFT + U + vdW level the edge-sharing connectivity that leads to infinite AgCl₂ stripes (Figure 1e) was found to be the most energy preferred one among the Ag(II)Cl₂ polymorphs. All ribbon polytypes are maximally 5 meV/FU apart in energy. Among the layered structures, the most preferred is the ramsdellite related structure, then the γ-MnO₂ related (Figure 1b,c and Figure 2a,b) and finally the CuF₂ and AgF₂ related structures. The ramsdellite related structure (monoclinic space group) is only circa 40 meV/FU higher in energy than the ribbon polymorphs (

Table 1. Calculated DFT + U volumes and energies including van der Waals correction (E), zero-point energies (ZPE) and formation energies calculated in respect to the elemental crystals (E¹_form = E − E_{Ag + Cl2}) as well as to AgCl and ½ Cl₂ (E²_form = E − E_{AgCl + ½ Cl2}) for five prototypical AgCl₂ polymorphs. The formation energies are calculated considering high-temperature crystal structure of Cl₂ [43]. Volume values in brackets come from experiment. The formation energy for AgCl is calculated as E_form = E − E_{Ag+ ½ Cl2}. FU = formula unit.

Phase	Z	V/FU (Å3)	E (eV/FU)	E1form/FU (eV)	E2form/FU (eV)	ZPE/FU (eV)	Vform/FU (Å3)
Ribbon AgCl2 (CdI2 related)	4	65.7	−7.683	−0.840	+0.136	0.080	+3.6
Layered AgCl2 (ramsdellite related)	4	66.7	−7.643	−0.800	+0.176	0.077	+4.6
Layered AgF2 type	4	63.0	−7.625	−0.782	+0.194	0.081	+0.9
Ag(I)[Cl(Cl2)½] (rocksalt AgCl layers)	8	65.0	−7.718	−0.875	+0.101	0.070	+2.9
Ag(I)[Cl(Cl2)½] (hex AgCl layers)	8	77.2 *	−7.582	−0.739	+0.237	0.069	+15.1 *
AgCl + ½ Cl2		62.1	−7.819			0.027
Cl2	4	47.6 (58.1)	−4.288			0.029
AgCl	4	38.3 (42.7)	−5.675	−0.976		0.021	−1.0
Ag fcc	4	15.5 (17.1)	−2.555			0.012

* The unusually large calculated volume of this phase clearly suggests that it originates from attempts of XtalOpt to separate Cl₂ and AgCl phases, hence this phase may not correspond to any real local minimum, i.e., it may not be observable.

). This energy order reflects preference of Ag(II)Cl₂ for edge connectivity of the [Ag(II)Cl₄] square-planar units. Notably, all ribbon and puckered layered polymorphs are maximally 60 meV/FU apart. There is a considerable energy gap of about 200 meV/FU between the structures with puckered and flat layers; this is a manifestation of the fact that Ag(II)-Cl⁻ bonding is markedly covalent and it is characterized by close-to sp² hybridization at Cl atoms, which in turn comes with bending of the Ag–Cl–Ag angles. Concerning the structures containing Ag(I), the unusual Ag(I)[Cl(Cl₂)_½] form with rock salt AgCl double layers is preferred over the one with hexagonal layers by 136 meV/FU. Furthermore, it represents the overall global minimum. The zero-point energy further plays in favor of this structure, by additional 10meV/FU. Within the DFT + U picture, all predicted AgCl₂ polymorphs have negative formation energies and are thus energetically preferred over the elemental silver and molecular chlorine. However, they are metastable with respect to AgCl crystal. Calculated DFT + U energies of the lowest energy AgCl₂ forms are listed in Table 1 along with AgCl, molecular chlorine in its high-temperature polymorphic form [43], and elemental silver.

Inspection of the calculated energies and volumes of various phases of the AgCl₂ stoichiometry (Table 1) reveals that:

• While all forms of AgCl₂ are stable with respect to elements, none of AgCl₂ polymorphs is energetically stable at T → 0 K and p → 0 atm with respect to products from Equation (3), i.e., AgCl and ½ Cl₂.
• The (relatively) most stable phase is that of Ag(I)[Cl(Cl₂)_½] (rocksalt AgCl layers), as it falls at circa 0.1 eV above AgCl + ½ Cl₂.
• The ZPE correction changes very little the relative ranking of structures (it varies by no more than 12 meV for various phases), and for absolute stability of phases with respect to products (it destabilizes them by additional circa 42–53 meV), as could be expected for the system composed of rather heavy elements, Ag and Cl.

We have recalculated the total electronic energies and volumes of selected polymorphs also on much more resources-consuming hybrid DFT level using HSE06 functional (

Table 2. Calculated HSE06 volumes and energies and formation energies calculated with respect to the elemental crystals (E¹_form = E − E_{Ag + Cl2}) as well as to AgCl and ½ Cl₂ (E²_form = E − E_{AgCl + ½ Cl2}) for five prototypical AgCl₂ polymorphs. The formation energies are calculated considering high-temperature crystal structure of Cl₂ [43]. Volume values in brackets come from experiment. The formation energy for AgCl is calculated as E_form = E − E_{Ag+ ½ Cl2}.

Phase	Z	V/FU (Å3)	E (eV/FU)	E1form/FU (eV)	E2form/FU (eV)	ZPE/FU (eV)	Vform/FU (Å3)
Ribbon AgCl2 (CdI2 related)	4	77.6	−9.848	−1.030	+0.052	ND	+8.1
Layered AgF2 type	4	68.7	−9.727	−0.909	+0.173	ND	−0.8
Ag(I)[Cl(Cl2)½] (rocksalt AgCl layers)	8	70.7	−9.839	−1.021	+0.061	ND	+1.2
Ag(I)[Cl(Cl2)½] (hex AgCl layers)	8	83.9 *	−9.837	−1.019	+0.063	ND	+14.4 *
AuCl2-type (disproportionated)	4	76.9	−9.736	−0.918	+0.164	ND	+8.2
AgCl + ½ Cl2		69.5	−9.900			ND
Cl2	4	56.8 (58.1)	−5.536			ND
AgCl	4	41.1 (42.7)	−7.132	−1.082		ND	−4.2
Ag fcc	4	16.9 (17.1)	−3.282			ND

* The unusually large calculated volume of this phase clearly suggests that it originates from attempts of XtalOpt to separate Cl₂ and AgCl phases, hence this phase may not correspond to any real local minimum, i.e., not be observable.

). Guided by the previous result, we did not perform daunting ZPE calculations this time.

The hybrid DFT results for AgCl₂ (Table 2) show that:

• While all forms of AgCl₂ are stable with respect to elements, none of AgCl₂ polymorphs is energetically stable at T → 0 K and p → 0 atm with respect to products from Equation (3), i.e., AgCl and ½ Cl₂; thus, confirming the DFT + U + vdW (van der Waals correction) results.
• The (relatively) most stable phase is that of ribbon Ag(II)Cl₂ form as it falls at a mere 52 meV above AgCl + ½ Cl₂.
• HSE06 calculations predict the unit cell volumes of Ag, Cl₂, and AgCl quite well. The large calculated volume of the ribbon polymorph should be taken with a grain of salt, and this structure is bound only by weak vdW inter-ribbon interactions. The layered AgF₂-type structure is the only one for which the formation reaction volume is slightly negative.

Here, the unusual Ag(I)[Cl(Cl₂)_½] form with hexagonal AgCl double layers and its rock salt layer analogue were found to be energetically almost degenerate within 2 meV/FU. The unusual Ag(I)[Cl(Cl₂)_½] form with hexagonal layers was found to be only 11 meV/FU higher in energy in respect to the ribbon polymorph. Recall that the ZPE of the Ag(I)[Cl(Cl₂)_½] forms is by circa 10–11 eV/FU lower with respect to the ribbon polymorph (Table 1), which points to factual energy degeneracy of all three solutions considering the hybrid DFT free energies and DFT + U ZPE energies.

Hybrid DFT was also used to model mixed valence (i.e., charge density wave) Ag(I)Ag(III)Cl₄ solution, which could not be captured properly on DFT + U level. We have chosen for this purpose crystal structure of AuCl₂, which forms molecular crystal with weakly bonded Au(I)₂Au(III)₂Cl₈ units [12]. Ag(III) cations are here in square planar [AuCl₄] coordination and Au(I) in linear [AuCl₂] coordination. These molecular units are stacked along one direction along which they polymerize into infinite chains under Au → Ag substitution. In the polymerized chains, the Ag(III) cations retain the square-planar coordination, while the Ag(I) cations pick up third chlorine ligand to form triangular instead of linear coordination. The triangular coordination is a consequence of Ag(I) moving closer to a chlorine atom belonging to the Ag(III) from the neighboring Ag(I)Ag(III)Cl₂ molecular unit. The Ag(I)-Cl bonds are then obviously longer (2.5 Å) in comparison to the Au(I)-Cl ones (2.3 Å) in the original AuCl₂ structure. On DFT + U level, the model converges to the one featuring chains of the comproportionated cations (Ag^IAg^III → Ag^IIAg^II). This comproportionation is structurally manifested by Ag(I) cation picking up a fourth chlorine atom with which it completes square planar coordination of newly formed Ag(II) cation (the newly created Ag-Cl bond is highlighted by red dashed line in Figure 8b, bottom). Such polymerized Ag(II)Cl₂ chains are isostructural with recently discovered tubular form of AgF₂ that forms under high pressure (Figure 8c,d) [11]. In AgCl₂, the mixed valence chains are slightly energetically preferred (by circa 10 meV/FU) over the comproportionated ones at the hybrid DFT level. However, both are 100 meV/FU higher in energy with respect to the lowest energy ribbon polymorph.

3.4. Impact of Temperature and Pressure on Stability and Polymorphism of AgCl₂

Due to very similar energies of different polymorphs of AgCl₂ at T → 0 K and p → 0 GPa (also at the HSE06 level), and relatively small energy favouring the products of Equation (3) (AgCl and ½ Cl₂), stability and polymorphism of AgCl₂ are expected to be dependent on (p, T) conditions. Here, we look briefly at the impact of external parameters on stability of AgCl₂.

The influence of temperature on stability of AgCl₂ is expected to be small in the range where Cl₂ is solid or liquid (i.e., up to its boiling point of −34 °C); the large reaction volume for the ribbon polymorph (Table 2), which is overestimated anyway, is insufficient to stabilize this phase via entropy factor [44]. Further increase of temperature will lead to preference for AgCl + ½ Cl₂ via the entropy (ST) factor of the Cl₂ gas. The ST factor for ½ Cl₂ at 300 K equals 347 meV [45] and thus, assuming that most of reaction volume change corresponds to the volume of Cl₂ gas released, it may be estimated that delta G⁰ of AgCl₂ formation is about + 0.4 eV at 300 K. While this is only 40% of what Morris predicted (i.e., circa 1 eV) [2], the value is still substantial. Our results point out at the lack of thermodynamic stability of AgCl₂ at any temperature conditions (in the absence of external pressure effects).

The situation is somewhat different when the impact of external pressure is considered. Here, the infinite-sheet AgF₂-like form could potentially be stabilized at elevated pressure, as its formation from solid AgCl and ½ Cl₂ is accompanied by small volume drop. The common tangent method [17,46] allows for a rather crude estimate for the formation pressure of AgCl₂ of 35 GPa (at T → 0 K), and likely even higher pressures at elevated temperature. The more precise estimate requires calculations in the function of pressure to be performed, also including the ribbon polymorph, which should exhibit substantial compressibility, and several viable high-pressure polymorphs [11,47,48]. Moreover, while drawing the computed volume-based conclusions one should always remember that despite great performance of HSE06 functional for describing crystal and electronic structure of solids, the reproduction of van der Waals interactions is still imperfect. And since they tend to collapse fast under even moderate pressures, it could be that other polymorphic forms, such as the ribbon one, would become competitive at rather low pressures, even preceding the transformation to the layered form. The previously documented pressure-induced transformations of CuF₂ [47] and AgF₂ [11] as well as a large body of data for transition metal difluorides and dichlorides (see also [48] and references therein) seem to suggest this scenario as a viable one.

3.5. Magnetic Properties of Selected Polymorphic Forms of AgCl₂

If chemistry teaches us something important, it is that virtually any chemical composition may be studied in its metastable form, given that the local minimum is protected by sizeable energy and/or entropy barriers. Thus, while AgCl₂ may not be thermodynamically stable at a broad range of (p,T) conditions, it is still insightful to theoretically study selected properties of AgCl₂, and compare them to those of the related halides (CuCl₂, AgF₂, AuCl₂, etc.).

For all Ag(II)Cl₂ forms featuring paramagnetic silver, the magnetic ordering is of interest, especially that magnetic properties of Ag(II) fluorides are now under intense scrutiny [49,50]. Thus, we have looked at spin ordering patterns, spin exchange pathways, as well as relevant superexchange constants for the ribbon and layered polymorphs of AgCl₂ (

Table 3. Calculated energies, relative energies, and magnetic moments on atoms for the ribbon and AgF₂-type model of AgCl₂ as calculated using DFT + U + vdW. The unit cell was optimized for the ground state model (AFM1 in a ribbon and AFM in AgF₂-type structure), while energies of the remaining magnetic models were calculated as single point energies from the ground state.

Form	Ordering Pattern	E/FU (eV)	E_rel/FU (meV)	Ag (mB)	Cl(mB)
Ribbon polymorph	AFM1 (AABB)	−7.683	0	±0.31	±0.21 for F joining two like Ag spins ±0.00 between opposite Ag spins
	AFM2 (ABAB)	−7.652	31	±0.31	±0.10 on all F
	FM (AAAA)	−7.640	43	+0.35	+0.26 on all F
AgF2-type	AFM	−7.625	0	±0.24	±0.10
	FM	−7.549	76	+0.35	+0.26

).

Not surprisingly, in the case of the ribbon polymorph the magnetic ground state found here is identical to that exhibited by structurally related frustrated Heisenberg chain system, CuCl₂, i.e., the spin pattern is AABB [51]. Correspondingly, as for CuCl₂ we consider the next neighbor (J₁) as well as the next near neighbor (J₂) superexchange constants (Figure 9), while neglecting all weaker magnetic interactions [51]. From the equations relating the energies of AFM1, AFM2, and FM states, and using the same Hamiltonian as authors [51]:

E_AFM1 = (+2 J₁) × N²/4 + constant (this is AFM5 or AFM4 model in [51], since weaker interactions are omitted)

E_AFM2 = (+2 J₁ − 2 J₂) × N²/4 + constant (this is AFM2 or AFM3 model in [51], since weaker interactions are omitted)

E_FM = (−2 J₁ − 2 J₂) × N²/4 + constant (this is FM model in [51], since weaker interactions are omitted)

where N is the number of unpaired spins per spin site (in the present case, N = 1), one may derive J₁ = −12 meV and J₂ = −62 meV. The respective values for CuCl₂ calculated with U = 7 eV for Cu [51], are: J₁ = +18.4 meV and J₂ = −24.5 meV. Our results indicate that—like for CuCl₂—|J₂| > |J₁| and the spin-exchange interactions are geometrically frustrated (Figure 9). Interestingly, however, J₁ is antiferromagnetic for AgCl₂ while ferromagnetic for CuCl₂. This result probably stems from the fact that antiferromagnetic next neighbor ordering implies null magnetic moments on bridging two Cl atoms, while the FM one introduces very large moments on chloride bridges (Table 3). The former is preferred, as elements which are typical nonmetals (here, in the form of a formally a closed shell Cl⁻ anion) do not support spin density on them, since it implies breaking of the stable electronic octet. Indeed, the spin density calculated for AgCl₂ in ribbon form suggests that spin density on one type of Cl atoms is as large as 2/3 of that on silver sites. While this could be expected based on previous studies of Ag(II) in chloride host lattices [52], this factor certainly contributes to lack of stability of AgCl₂. After all, if most spin sits on Cl atoms, Cl radical tend to pair up and eliminate Cl₂ molecules. This is indeed what one sees when comparing the energy of polymorphic forms of AgCl₂ with respect to phase separated AgCl + ½ Cl₂. The situation found for CuCl₂ is much different, where the total magnetic moment of circa 0.5μ_B sits mostly on copper site [51].

Let us now scrutinize the magnetic interactions in the layered AgCl₂ polymorph (Table 3, Figure 9).

Here, four identical superexchange pathways link each Ag(II) site to its neighbors, as characterized by intra-sheet superexchange constant, J (the much weaker inter-sheet one will be omitted here). The ground state magnetic model corresponds to the familiar two-dimensional (2D) AFM ordering of spins, assumed also by AgF₂. Consequently, a spin flip to the FM state costs (−4 J) × N²/4, where N = 1. From the energy difference between the AFM and FM solutions we may extract J = −76 meV. For comparison the J found for AgF₂ at ambient conditions is −70 meV [53]. This implies a somewhat stronger magnetic superexchange for the Ag–Cl–Ag bridges than for the Ag–F–Ag ones, as indeed could be anticipated from the increased covalence of chemical bonding (Ag–Cl > Ag–F). This effect is, however, partially diminished by the Ag–Cl–Ag bridges being more bent (124 deg) than their Ag–F–Ag analogues found for AgF₂ (130 deg), and that decreases J for the former system [54], according to the Goodenough-Kanamori rules [55]. Corrugation of the sheets and departure of the Ag–Cl–Ag angle from 180 deg also results in the appearance of the magnetic moment of circa 0.1μ_B at Cl atoms. This is half of what is found for the ribbon polymorph, yet still substantial, and must be viewed as a factor which contributes to the lack of stability of AgCl₂ with respect to elimination of Cl₂.

3.6. Electronic Properties of Selected Polymorphic Forms of AgCl₂

Having looked at magnetic properties, let us now examine electronic Density of States (DOS) and atomic (partial) DOS for four distinct polymorphs of AgCl₂ (Figure 10).

A glance at DOS graphs shows that all predicted polymorphs of AgCl₂ were found to have an insulating band gap. However, the calculated band gap at Fermi level tends to be substantially narrower in studied polymorphs of AgCl₂ than in their structural prototypes containing either a different group 11 metal (CuCl₂, AuCl₂) or a different halogen (AgF₂). In the case of CuCl₂-like ribbon structure, Ag 4d bands lie comparatively lower in energy than Cu 3d bands and are further separated from occupied Cl 2p states, which is in agreement with the stronger oxidizing properties of Ag(II) species as compared to Cu(II). The picture is somewhat similar in the layered structure: again, the Ag 4d states in AgCl₂ lie at higher binding energies and are more separated from Cl 2p states than in AgF₂, where the admixing between Ag 4d and F 1p states in AgF₂ is already substantial [53]. The same applies to the disproportionated form of AgCl₂ (i.e., an AuCl₂ polytype) as compared to its gold(II) analogue. The fact that Ag states are placed deeply below the Cl ones clearly contributes to the lack of stability of AgCl₂ in all polytypes, as oxidation of Cl⁻ anions by Ag(II) (or Ag(III) in disproportionated form) is facile. This is also reflected in very narrow fundamental bandgaps, which range between a mere 0.24 eV and 0.40 eV. The Maximum Hardness Principle (from Pearson [56]) dictates the preference for much larger bandgap calculated for AgCl + ½ (Cl₂) (1.69 eV) and thus to a redox reaction.

As for the AgCl₂ polymorph consisting of hexagonal double layers of AgCl interspersed with layers of Cl₂ molecules, we compared its electronic structure with the combination of eDOS of rocksalt-type AgCl and solid chlorine (HT polymorph). Contributions from in-layer Cl atoms and from Cl₂ molecules between layers in this AgCl₂ polymorph are also plotted separately. The most apparent difference between otherwise similar graphs is that the bands pertaining to Cl₂ molecules are much sharper in AgCl₂ than in solid Cl₂, which indicates that there is relatively little bonding between them and AgCl layers. On the other hand, Ag 4d bands in AgCl layers of AgCl₂ are somewhat more diffuse than in rocksalt AgCl, which points to a slightly different (more covalent) Ag-Cl bonding character in hexagonal [AgCl] sublattice of AgCl₂ (as discussed in structural section above) than in ionic AgCl. In addition, the average position of Ag 4d band in this polymorph is circa −3 eV, which is 0.5–1.0 eV higher than in the other three studied polymorphs; this obviously stems from the fact that Ag(I) is present here rather than Ag(II). In this case, the gap is formed between top of the hybridized Ag⁺(d)/Cl⁻(p) states and the sigma* states of the Cl₂ molecules.

As to the relatively most stable forms of AgCl₂, i.e., a ribbon and layered polymorph, their band gaps have charge-transfer character; however, in idealized charge-transfer magnetic insulator the gap is formed between occupied nonmetal states (valence band) and the upper Hubbard band on metal (conduction band). Here, there is so severe mixture of the Ag and Cl states, that the top of the “ligand” band is composed in about 1/3 from Ag states, while the conduction band from a nearly equal mixture of the Ag and Cl states.

4. Conclusions

Our theoretical study for AgCl₂ including outcome of evolutionary algorithm structure prediction method suggests that AgCl₂ is metastable with respect to AgCl + ½ Cl₂ at p → 0 atm and T → 0 K conditions. Still, the energy penalty which must be paid for its synthesis from these substrates is relatively small and of the order of 0.1–0.15 eV per formula unit. Thermodynamic stability is smaller at ambient (p,T) conditions and of the order of 0.4 eV per formula unit, due to entropy factor for Cl₂ gas (reaction product). Still, AgCl₂ is not as severely unstable as previously predicted by Morris [2]. If prepared using some non-equilibrium methods, AgCl₂ would be metastable as indicated by lack of imaginary phonon modes for the structures we have scrutinized. AgCl₂ constitutes a challenge for theoretical methods as it allows for diverse charge instabilities, as well as on the verge of decomposition to simpler phases. The most stable polymorphic form of AgCl₂, according to hybrid DFT (HSE06) calculations, is related to CuCl₂ type, and it consists of infinite [AgCl_4/2] ribbons. The lowest energy magnetic pattern for this phase is of the AABB type, thus similar to the one shown by CuCl₂. More complex magnetic ordering, i.e., helical, is also possible, due to frustration of NN and NNN superexchange interactions.

Formation of AgCl₂ should be facilitated by use of external pressure, as indicated by extrapolation based on the common tangent method. The thermodynamically stable form at circa 35 GPa has crystal structure related to that of AgF₂; and, like AgF₂, it shows 2D AFM ordering in its ground state.

Having uncovered the chemical identity of the most stable form of AgCl₂ together with its presumed magnetic properties, we may construct a simple table which demonstrates huge difference between coinage group metals [55,57] in terms of their real and hypothetical difluorides and dichlorides (

Table 4. Comparison of essential features (stability, structure) and magnetic properties (wherever applicable) of Group 11 difluorides and dichlorides, as seen from experiment and theoretical calculations.

Metal	Cu	Ag	Au
MF2	Stable Layered 2D AFM [47]	Stable Layered 2D AFM [53]	Unstable Phase separation
MCl2	Stable Ribbon 1D complex [51]	Metastable Phase separation [this work]	Stable Disproportionated Diamagnetic [12]

). Thus, copper, silver, and gold are all different; indeed, the coinage metal group has been argued to contain the most dissimilar elements among all groups of the Periodic Table [58] and this is confirmed in our study of their dichlorides.

In conclusion, if prepared, AgCl₂ would be a very unusual metastable narrow-band gap (<0.4 eV) magnetic semiconductor. Quest for AgCl₂ should preferably utilize non-equilibrium, high-pressure, and low-T conditions. In the forthcoming work we will report our own attempts toward synthesis of AgCl₂ utilizing the diamond anvil cell setup.