Polymer Optical Fiber Bragg Gratings in CYTOP Fibers for Angle Measurement with Dynamic Compensation
Abstract
:1. Introduction
2. Theoretical Background and Compensation Technique
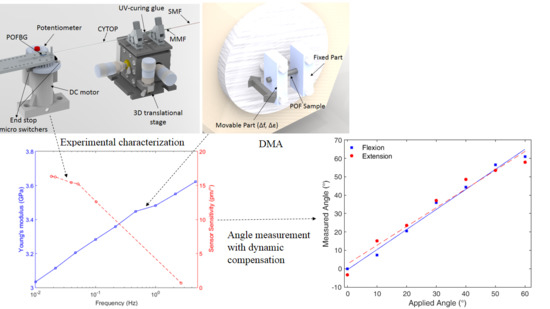
3. Experimental Setup
4. Results and Discussion
4.1. Sensor Characterization
4.2. Compensation Technique Verification
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Large, M.C.J.; Moran, J.; Ye, L. The role of viscoelastic properties in strain testing using microstructured polymer optical fibres (mPOF). Meas. Sci. Technol. 2009, 20, 34014. [Google Scholar] [CrossRef]
- Marques, C.A.F.; Peng, G.-D.; Webb, D.J. Highly sensitive liquid level monitoring system utilizing polymer fiber Bragg gratings. Opt. Express 2015, 23, 6058–6072. [Google Scholar] [CrossRef] [PubMed]
- Vilarinho, D.; Theodosiou, A.; Leitão, C.; Leal-Junior, A.; Domingues, M.; Kalli, K.; André, P.; Antunes, P.; Marques, C. POFBG-Embedded Cork Insole for Plantar Pressure Monitoring. Sensors 2017, 17, 2924. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, R.; Lee, H.; Lacraz, A.; Theodosiou, A.; Kalli, K.; Mizuno, Y.; Nakamura, K. Pressure Dependence of Fiber Bragg Grating Inscribed in Perfluorinated Polymer Fiber. IEEE Photonics Technol. Lett. 2017, 29, 2167–2170. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Frizera-Neto, A.; Marques, C.; Pontes, M. A Polymer Optical Fiber Temperature Sensor Based on Material Features. Sensors 2018, 18, 301. [Google Scholar] [CrossRef] [PubMed]
- Stefani, A.; Andresen, S.; Yuan, W.; Herholdt-Rasmussen, N.; Bang, O. High sensitivity polymer optical fiber-bragg-grating-based accelerometer. IEEE Photonics Technol. Lett. 2012, 24, 763–765. [Google Scholar] [CrossRef]
- Rajan, G.; Noor, Y.M.; Liu, B.; Ambikairaja, E.; Webb, D.J.; Peng, G.D. A fast response intrinsic humidity sensor based on an etched singlemode polymer fiber Bragg grating. Sens. Actuators A Phys. 2013, 203, 107–111. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Frizera, A.; Pontes, M.J. Dynamic Compensation Technique for POF Curvature Sensors. J. Lightwave Technol. 2018, 36, 1112–1117. [Google Scholar] [CrossRef]
- Kirtley, C. Clinical Gait Analysis: Theory and Practice; Elsevier: Philadelphia, PA, USA, 2006. [Google Scholar]
- El-Gohary, M.; McNames, J. Shoulder and elbow joint angle tracking with inertial sensors. IEEE Trans. Biomed. Eng. 2012, 59, 2635–2641. [Google Scholar] [CrossRef] [PubMed]
- Stupar, D.Z.; Bajic, J.S.; Manojlovic, L.M.; Slankamenac, M.P.; Joza, A.V.; Zivanov, M.B. Wearable low-cost system for human joint movements monitoring based on fiber-optic curvature sensor. IEEE Sens. J. 2012, 12, 3424–3431. [Google Scholar] [CrossRef]
- Leal Junior, A.; Frizera Neto, A.; Pontes, M.J.; Botelho, T.R. Hysteresis compensation technique applied to polymer optical fiber curvature sensor for lower limb exoskeletons. Meas. Sci. Technol. 2017, 28, 125103. [Google Scholar] [CrossRef] [Green Version]
- Leal-Junior, A.G.; Frizera, A.; Marques, C.; Sanchez, M.R.A.; dos Santos, W.M.; Siqueira, A.A.G.; Segatto, M.V.; Pontes, M.J. Polymer Optical Fiber for Angle and Torque Measurements of a Series Elastic Actuator’s Spring. J. Lightwave Technol. 2018, 36, 1698–1705. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Vargas-Valencia, L.; dos Santos, W.M.; Schneider, F.; Siqueira, A.A.G.; Pontes, M.J.; Frizera, A. POF-IMU sensor system: A fusion between inertial measurement units and POF sensors for low-cost and highly reliable systems. Opt. Fiber Technol. 2018, 43, 82–89. [Google Scholar] [CrossRef]
- Webb, D.J. Fibre Bragg grating sensors in polymer optical fibres. Meas. Sci. Technol. 2015, 26, 92004. [Google Scholar] [CrossRef] [Green Version]
- Marques, C.; Leal-Junior, A.; Min, R.; Domingues, M.; Leitão, C.; Antunes, P.; Ortega, B.; André, P. Advances on Polymer Optical Fiber Gratings Using a KrF Pulsed Laser System Operating at 248 nm. Fibers 2018, 6, 13. [Google Scholar] [CrossRef]
- Luo, Y.; Yan, B.; Zhang, Q.; Peng, G.-D.; Wen, J.; Zhang, J. Fabrication of Polymer Optical Fibre (POF) Gratings. Sensors 2017, 17, 511. [Google Scholar] [CrossRef] [PubMed]
- Pospori, A.; Marques, C.A.F.; Bang, O.; Webb, D.J.; André, P. Polymer optical fiber Bragg grating inscription with a single UV laser pulse. Opt. Express 2017, 25, 9028–9038. [Google Scholar] [CrossRef] [PubMed]
- Marques, C.A.F.; Min, R.; Leal Junior, A.; Antunes, P.; Fasano, A.; Woyessa, G.; Nielsen, K.; Rasmussen, H.K.; Ortega, B.; Bang, O. Fast and stable gratings inscription in POFs made of different materials with pulsed 248 nm KrF laser. Opt. Express 2018, 26, 2013–2022. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, X.; Woyessa, G.; Kinet, D.; Janting, J.; Nielsen, K.; Bang, O.; Caucheteur, C. BDK-doped core microstructured PMMA optical fiber for effective Bragg grating photo-inscription. Opt. Lett. 2017, 42, 2209–2212. [Google Scholar] [CrossRef] [PubMed]
- Large, M.C.J.; Poladian, L.; Barton, G.W.; van Eijkelenborg, M.A. Microstructured Polymer Optical Fibres; Springer: New York, NY, USA, 2008. [Google Scholar]
- Luo, Y.; Yan, B.; Li, M.; Zhang, X.; Wu, W.; Zhang, Q.; Peng, G.D. Analysis of multimode POF gratings in stress and strain sensing applications. Opt. Fiber Technol. 2011, 17, 201–209. [Google Scholar] [CrossRef]
- Theodosiou, A.; Lacraz, A.; Stassis, A.; Koutsides, C.; Komodromos, M.; Kalli, K. Plane-by-Plane Femtosecond Laser Inscription Method for Single-Peak Bragg Gratings in Multimode CYTOP Polymer Optical Fiber. J. Lightwave Technol. 2017, 35, 5404–5410. [Google Scholar] [CrossRef]
- Theodosiou, A.; Hu, X.; Caucheteur, C.; Kalli, K. Bragg gratings and Fabry-Perot cavities in low-loss multimode CYTOP polymer fibre. IEEE Photonics Technol. Lett. 2018, 30, 857–860. [Google Scholar] [CrossRef]
- Lacraz, A.; Polis, M.; Theodosiou, A.; Koutsides, C.; Kalli, K. Femtosecond Laser Inscribed Bragg Gratings in Low Loss CYTOP Polymer Optical Fiber. IEEE Photonics Technol. Lett. 2015, 27, 693–696. [Google Scholar] [CrossRef]
- Ziemann, O.; Krauser, J.; Zamzow, P.E.; Daum, W. POF Handbook: Optical Short Range Transmission Systems; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 9783540766292. [Google Scholar]
- Lakes, R. Viscoelastic Materials; Cambridge University Press: Cambridge, UK, 2009; ISBN 9780511626722. [Google Scholar]
- Bundalo, I.-L.; Nielsen, K.; Woyessa, G.; Bang, O. Long-term strain response of polymer optical fiber FBG sensors. Opt. Mater. Express 2017, 7, 401–403. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Marques, C.; Frizera, A.; Pontes, M.J. Dynamic Mechanical Analysis on a PolyMethyl Methacrylate (PMMA) Polymer Optical Fiber. IEEE Sens. J. 2018, 18, 2353–2361. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Frizera, A.; Pontes, M.J.; Fasano, A.; Woyessa, G.; Bang, O.; Marques, C.A.F. Dynamic mechanical characterization with respect to temperature, humidity, frequency and strain in mPOFs made of different materials. Opt. Mater. Express 2018, 8, 804–815. [Google Scholar] [CrossRef] [Green Version]
- Ashby, M.F. Materials Selection in Mechanical Design; Elsevier: Cambridge, UK, 2005; ISBN 0750661682. [Google Scholar]
- ASTM International ASTM D4065. Standard Practice for Plastics: Dynamic Mechanical Properties: Determination and Report of Procedures; Annual Book of ASTM Standards; ASTM: West Conshohocken, PA, USA, 2012; pp. 1–7. [Google Scholar] [CrossRef]
- Ioannou, A.; Theodosiou, A.; Caucheteur, C.; Kalli, K. Direct writing of plane-by-plane tilted fiber Bragg gratings using a femtosecond laser. Opt. Lett. 2017, 42, 5198–5201. [Google Scholar] [CrossRef] [PubMed]
- Pospori, A.; Marques, C.A.F.; Sáez-Rodríguez, D.; Nielsen, K.; Bang, O.; Webb, D.J. Thermal and chemical treatment of polymer optical fiber Bragg grating sensors for enhanced mechanical sensitivity. Opt. Fiber Technol. 2017, 36, 68–74. [Google Scholar] [CrossRef] [Green Version]
- Stajanca, P.; Cetinkaya, O.; Schukar, M.; Mergo, P.; Webb, D.J.; Krebber, K. Molecular alignment relaxation in polymer optical fibers for sensing applications. Opt. Fiber Technol. 2016, 28, 11–17. [Google Scholar] [CrossRef] [Green Version]
- Leal-Junior, A.; Frizera, A.; Marques, C.; José Pontes, M. Polymer-optical-fiber-based sensor system for simultaneous measurement of angle and temperature. Appl. Opt. 2018, 57, 1717–1723. [Google Scholar] [CrossRef] [PubMed]
- Kalantar-Zadeh, K. Sensors: An Introductory Course; Springer: New York, NY, USA, 2013; ISBN 9781461450528. [Google Scholar]
- Leal-Junior, A.G.; Frizera, A.; Marques, C.; Pontes, M.J. Viscoelastic features based compensation technique for polymer optical fiber curvature sensors. Opt. Laser Technol. 2018, 105, 35–40. [Google Scholar] [CrossRef]












| Symbol | Parameter | Value |
|---|---|---|
| Pe | Photoelastic constant | 0.30 |
| λB | Bragg wavelength | 1550.00 nm |
| υ | Poisson’s ratio | 0.42 |
| E1 | Young’s modulus at f1 | 3.00 GPa |
| E2 | Young’s modulus at f2 | 2.00 GPa |
| I | Moment of inertia | 4.53 × 10−14 m4 |
| M | Bending constant | 100 Nm |
| h1 | Hysteresis at f1 | 0.10 |
| h2 | Hysteresis at f2 | −0.05 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leal-Junior, A.; Theodosiou, A.; Díaz, C.; Marques, C.; Pontes, M.J.; Kalli, K.; Frizera-Neto, A. Polymer Optical Fiber Bragg Gratings in CYTOP Fibers for Angle Measurement with Dynamic Compensation. Polymers 2018, 10, 674. https://doi.org/10.3390/polym10060674
Leal-Junior A, Theodosiou A, Díaz C, Marques C, Pontes MJ, Kalli K, Frizera-Neto A. Polymer Optical Fiber Bragg Gratings in CYTOP Fibers for Angle Measurement with Dynamic Compensation. Polymers. 2018; 10(6):674. https://doi.org/10.3390/polym10060674
Chicago/Turabian StyleLeal-Junior, Arnaldo, Antreas Theodosiou, Camilo Díaz, Carlos Marques, Maria José Pontes, Kyriacos Kalli, and Anselmo Frizera-Neto. 2018. "Polymer Optical Fiber Bragg Gratings in CYTOP Fibers for Angle Measurement with Dynamic Compensation" Polymers 10, no. 6: 674. https://doi.org/10.3390/polym10060674
APA StyleLeal-Junior, A., Theodosiou, A., Díaz, C., Marques, C., Pontes, M. J., Kalli, K., & Frizera-Neto, A. (2018). Polymer Optical Fiber Bragg Gratings in CYTOP Fibers for Angle Measurement with Dynamic Compensation. Polymers, 10(6), 674. https://doi.org/10.3390/polym10060674